基于EMD与模型预测控制算法的风电功率平抑

张家军，陈 杰，常喜强，李 霞，毛吾兰·买买提依明，徐 鹏，杨艳磊

(1.国网乌鲁木齐供电公司，新疆 乌鲁木齐 830011；2.国网新疆电力有限公司，新疆 乌鲁木齐 830002)

0 引 言

开发利用可再生能源是应对能源问题的有效手段。而可再生能源的消纳是制约可再生能源发展的关键因素之一[1-2]。风能、太阳能等可再生能源会实时地受到气候、季节、地形、区域等诸多因素的影响，故其输出往往伴随着随机、不稳定、间歇性等特点，当一定规模的可再生能源发电并网后对电网的电能质量带来了不利影响[3-4]。研究增强可再生能源发电输出功率稳定性的方法及减小可再生能源发电对电网电能质量的影响，对发展可再生能源战略具有重要意义[5]。

储能技术可将电能储存起来，在需要时释放，以平抑可再生能源发电的功率，保证电能的持续稳定输出，增加电网对可再生能源发电的接纳能力。文献[6-7]将蓄电池和超级电容同时引入到发电系统中构成混合储能系统，用能量密度较高的蓄电池储能平抑能量高、变化慢的低频波动，用功率密度大的超级电容储能平抑能量低、变化快的高频波动。目前，已有多种平抑风电输出功率波动平抑的控制策略。文献[8]采用低通滤波器的控制方法，并且用储能的实时荷电状态(state of charge，SOC)来计算滤波的时间常数，以输出功率波动为控制目标，在利用模糊控制对储能的功率进行分配；但是以低通滤波器为基础的控制算法对功率波动的平抑效果不佳。文献[9]利用小波包分解将输出功率分解出低频部分和高频部分信号，然后结合统计分析和支持向量机辨别出功率波动的超限部分，控制风氢混合储能系统；但上述的小波分解、卡尔曼滤波、一阶滤波等平抑算法在实时控制方面存在局限性。文献[10]利用超级电容和储能电池的能量密度和功率密度的特点，根据储能电池的荷电状态，将控制过程分为优化控制层和协调控制层来保证储能系统的整体充放能力。模型预测控制(model predictive control，MPC)算法具有提前预测、优先控制等特点，且实时性较好[11]。

以上文献充分说明储能技术能够平抑风电场的输出功率。下面构造以经验模态分解(empirical mode decomposition，EMD)算法为基础对储能能量进行分配，用能量密度高但功率密度低的蓄电池储能平抑低频功率波动，用能量密度低但功率密度高的超级电容平抑高频功率波动。以MPC算法作为平抑控制策略，以储能使用量最小为控制目标，对混合储能系统的充放电进行分配和控制，以达到在储能功率约束、储能系统荷电状态约束以及并网功率波动约束下，平抑风电场的并网功率，减小并网功率冲击。最后，用某风电场一天的实际输出功率数据验证所提方法的可行性和有效性。

1 混合储能平抑风电波动模型构建

利用混合储能技术对风电功率波动平抑是一种有效手段[12-14]。风电混合储能发电系统包括双馈风力发电机组、混合储能系统和混合储能发电系统。风电混合储能系统结构如图1所示。

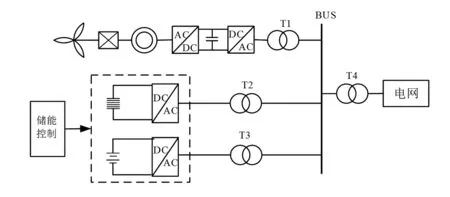
图1 混合储能平抑风电、波动系统结构

当电网消纳不了风电时，可将富余的电能分配给储能系统用于储能。系统由风力发电系统、混合储能系统、功率分配控制器及连接线组成。当风电过剩时，能量由母线流向混合储能系统；当风电不足时，能量由混合储能系统流向母线并供给电网。混合储能系统由蓄电池储能和超级电容储能构成。蓄电池储能响应速度较慢，但其可储存容量大，蓄电池储能承担低频的功率波动。而超级电容储能响应速度快，适用于频繁充放电，超级电容承担高频的功率波动。储能系统能对风电的输出功率达到“削峰填谷”的效果，使其输入电网的功率更加平滑。

2 混合储能平抑风电波动优化控制策略

2.1 经验模态分解原理

经验模态分解是一种无须选择基函数就能够自适应地将原始信号分解成一组固有模态函数(intrinsic mode function，IMF)的线性组合，分解后的信号能够突显出原始信号的局部特征。

在EMD分解中，所有的模态函数均满足两个条件：1)在整个数据序列中，极值点数和过零点数相等或者相差为1；2)在整个数据序列中，信号的局部极大值和局部极小值构成的包络线关于时间轴对称，即其均值为0。

EMD分解的流程如下：

1)寻找信号的所有极大值点和极小值点，对极大值点做插值形成上包络线，对极小值点做插值形成下包络线。

2)计算出上、下包络线的均值m，用原始信号s(t)减去m，求出中间信号h(t)。

h(t)=s(t)-m

(1)

3)然后判断h(t)是否满足IMF的条件，如不满足，则对h(t)重复步骤1、步骤2，直到满足IMF的条件，就得到第1个IMF信号c1(t)。

c1(t)=h(t)

(2)

4)用原始信号减去第1个IMF分量，得到第1个剩余信号r1(t)。

r1(t)=s(t)-c1(t)

(3)

将r1(t)作为新的原始信号，重复步骤1至步骤4，然后分解出剩下的模态分量c2，c3，…，直至剩余信号呈现为单调时完成分解，并将其记为剩余分量r(t)。

综上，经验模态分解可把信号s(t)分解为一组模态函数ci(t)和一个剩余分量r(t)的线性组合，表示为

(4)

式中：ci(t)为信号中各振荡模态分量；r(t)为信号中的剩余分量。

2.2 优化控制及其约束

模型预测控制(MPC)算法能够根据历史信息和现有输入来提前对输出作出预测，能够实现提前预测、优先控制。该方法具有较好的实时性，因此将其作为功率平抑控制方法。MPC主要由状态空间模型和滚动时域策略两部分组成[15]。

风电并网功率与风电场输出功率、储能功率的关系为

Pg(k)=Pes(k)+Pw(k)

(5)

式中：Pg(k)为在k时刻的并网功率；Pes(k)为在k时刻的储能功率；Pw(k)为在k时刻的风电发出功率。

则在k+1时刻储能系统的荷电状态为

(6)

式中：Ses(k)为k时刻的荷电状态；Ces为储能容量；Tc为控制周期。

1)状态空间模型：将并网功率Pg和荷电状态Ses作为状态变量x1和x2；储能功率Pes作为控制量u；风电实际发出Pw作为扰动量r；下一时刻的并网功率Pg和荷电状态Ses作为输出y1和y2。构建状态空间表达式为

(7)

2)滚动时域策略：首先，利用式(7)的状态空间模型对k+M(M=1，2，3，…)时刻的输出Pg和Ses进行预测，再结合二次规划对每个控制时域的输出结果进行优化，即可得到相应的功率控制指令。然后将其转化为优化模型求解。其中，以各优化周期内储能使用量最少作为优化的目标函数，如式(8)所示。

(8)

并且同时需要满足储能功率约束、对风电并网功率波动率γ的限制和储能荷电状态约束，即约束条件为

(9)

式中：Pes_max和Pes_min分别为储能功率能达到的上下限；Pg_min和Pg_max分别为并网功率的最小值和最大值；Prated为风电的装机额定功率。

3 算例分析

选取某风电场一日的实际功率数据为研究对象，采样时长为1440 min，采样率为1 min，装机容量为200 MW。图2为某风电场实际输出功率的波形图。

图2 风电实际输出功率

3.1 平抑策略

根据式(9)的约束条件，以1 min波动率≤2%和30 min波动率≤7%作为风电并网波动率限制，储能功率约束Pes取9 MW，储能SOC范围为0.1～0.9，采用模型预测控制算法对该风电功率曲线进行平抑，平抑后的风电功率如图3所示。

图3 平抑后的风电输出功率

可以看出，平抑后的风电功率波动较为平滑，平抑后的1 min和30 min的波动率分别如图4、图5所示。

由图4、图5可知，平抑后的波动率大幅度降低，平抑后的1 min的最大波动率为1.19%，30 min的最大波动率为6.17%。满足并网要求的平抑后1 min波动率≤2%，30 min波动率≤7%。

图4 平抑后1 min的波动率

图5 平抑后30 min的波动率

3.2 能量分配

蓄电池储能可储存容量大，充放电响应较慢，承担了波动的低频功率指令；而超级电容充放电响应时间在数毫秒到几十分钟，承担了波动频繁的高频功率指令。算例结果也符合蓄电池储能和超级电容的性能特点，储能的能量分配如图6、图7所示。

图6 蓄电池储能承担的功率

图7 超级电容储能承担的功率

4 结 语

风电具有的随机性与波动性，使其在并网时给大电网在电压、频率的稳定性及可靠性上带来了巨大的挑战。储能系统可以作为能量缓冲装置，能够弥补风电等可再生能源发电的波动性和间歇性，使其输出更容易调度和可控，减小对电网电能质量的影响。前面构造的以EMD算法来对功率做预处理，将其分解为低频部分和高频部分，然后结合实时性较好的模型预测控制算法控制功率指令，对风电功率进行平抑。对实际风电场数据的仿真结果论证了该方法可以有效平抑风电场输出功率，明显提升风力发电的稳定性，减小对电网的冲击，为可再生能源的大规模开发利用提供了技术支持。