基于EMD的长周期地震动分量提取方法

谭潜，李英民，杨永斌

(1.中机中联工程有限公司，重庆 400039；2. 重庆大学 土木工程学院,重庆 400045)

在实际地震记录形成过程中，存在各种成分地震波的叠加(图1)[1]，故地震记录的主要特性由其主要成分特性来表达更具代表性。对地震动原始记录的分析处理是以往研究地震动的主要方向，其忽视了地震动分量分析，而地震记录中存在长周期分量的事实不能否认[2]。在长周期地震动界定中，徐龙军等[3]以规准反应谱的离散性分析为基础，指出地震动的反应谱特征与地震记录的长周期分量是不可忽视的两个方面。对地震记录各类分量的提取和分析是确定地震动类型的可靠方法。地震动分量提取方法与信号分析方法息息相关。学者们在信号处理方法的基础上提出了相关分量提取方法，Khanse等[4]利用傅里叶变换方法确定频率，结合巴特沃斯滤波器对地震记录进行分量分离，提取出长周期地震动脉冲分量，进而对相应的位移反应进行分析评估；陈红等[5]采用分数阶伽柏变换对地震信号进行时频分析，其中一项重要的应用就是利用分数阶伽柏变换来进行分数域谱分解，同时，也可以提取频域中的不同尺度和不同方向上的特征，优势明显；Baker[6]以小波理论为基础，提取地震记录分量，从而对脉冲和非脉冲的地震记录进行识别，具有较好的区分度，但是，不能对地震动分量的特性进一步的描述是此方法的不足；Mallat分解与重构是一种基于多尺度分析的小波变换分离分量的关键技术，赵国臣等[7]将其引入到地震记录分量提取中，认为是一种有效的方法；Farid等[8]应用滑动平均滤波方法，结合截止频率，将原地震记录分解，提取脉冲型分量，剩下作为剩余分量。将提取的分量输入结构，探索结构的弹性反应。商业软件Seismo Signal中自带数字滤波器，可以对地震动进行滤波，提取相应的分量，徐龙军等[3]利用软件的此功能提取脉冲分量，并对地震记录反应谱及提取的分量反应谱的离散性进行分析和校验。

在经验模态分解(empirical mode decomposition， EMD)等信号处理与分量分离技术在地震动信号处理中应用的基础上，采用合适评价长周期地震动的截止周期，实现了表征长周期地震动特性的长周期分量的提取，验证了提取分量的合理性与有效性，提出可应用于长周期地震动识别及其规律特性研究的地震动分量提取方法。

图1 长周期地震动的叠合Fig.1 Superposition of the long period ground motions

1 EMD理论

EMD作为一种新型自适应非平稳信号处理方法，不仅对线性平稳信号处理效果较好，而且对地震波等非线性、非平稳信号的分析处理有很好的适用性。本征模态函数(IMF)是EMD的前提。EMD方法认为信号都是由若干IMF组成，如果IMFs相互重组叠加，便可以重构为复合信号[9]。所以，EMD的重要目标就是为了得到IMFs，实现这个目标受到两个条件的限制：首先，峰值点的个数与函数穿零数必须相等或者最多相差一个；其次，局部极大值构成的上包络线和极小值构成的下包络线的平均值为零，以IMFs为基础可展开EMD，其过程如下：

1)基于给定的地震记录信号x(t)，分别标记出其所有局部极大值xmax(t)和局部极小值xmin(t)；

2)将所有的局部极大值(xmax(t))点、局部极小值(xmin(t))点分别用3次样条曲线连接起来，形成上、下包络线；

3)对包络线上的局部极大值、局部极小值取平均

(1)

4) 移除初始地震记录信号中的平均趋势

d(t)=x(t)-m(t)

(2)

5)移除平均趋势的d(t)如果满足上述两个限定条件，令ci(t)=d(t)作为一个IMF，则可以算出残量r(t)=x(t)-d(t)；反之，如d(t)不满足两个限制条件，则进入第下一步继续筛选；

6)反复运行1)～5)步，让d(t)满足限制条件要求，最终得到多个IMF和残量rn(t)，rn(t)为单调函数或者为常数

x(t)-c1(t)=r1(t)

r1(t)-c2(t)=r2(t)

…

rn-1(t)-cn(t)=rn(t)

(3)

反过来，可以通过n个IMF分量(ci(t))与残量(rn(t))的线性组合得到原始信号

(4)

2 截止周期确定

数字信号处理领域常用数字滤波技术调制频率分量，文献[4]采用频率1.67 Hz作为识别脉冲特征的界限。Rathje等[10-11]通过对地震记录的频谱周期参数对比后发现，加速度反应谱平均周期Tavg(式(5))在反映长周期地震动的低频特性方面具有无可比拟的优势，且采用频谱参数Tavg能将地震记录的高、低频分量分布情况更准确地区分，低频分量更容易被识别。杜东升等[12]研究表明，Tavg的变化与震级的变化具有一致性，Tavg是敏感性更好的频谱参数，在评价长周期地震动时更具优势。由Tavg计算公式可以知道其物理意义表示的是周期关于对应谱值平方的一个加权平均值，反映了地震动频谱在整个计算频域内的分布情况[11]。

0.05 s≤Ti≤10 s

(5)

式中：Ti为加速度谱对应的离散等间隔周期点；Sa(Ti)为周期点的加速度反应谱；PGA为地震动加速度时程对应的峰值。

为了更好地体现Tavg对地震动特性区分的实用性，以Tavg在0.4～5.1 s范围内的10条汶川地震记录为数据基础，结合地震动的速度时程、归一化傅里叶幅值谱和速度谱(图2)，分析地震动频谱特性随Tavg变化而变化的规律：1)从速度时程看，地震动的速度时程曲线随Tavg的增大而越来越稀疏，穿零点越来越少，表示其长周期成分不断丰富，表明Tavg的变化能在一定程度上反映地震动周期的变化；2)从傅里叶谱(0.1～20 Hz)看,灰色背景的主频区域随Tavg的增大而向低频方向平移，低频成分占比逐渐增加，显示出地震记录主要频谱成分随Tavg的变化而变化的趋势，以Tavg=2 s为界，1 Hz以下的低频成分占比迅速增加，1 Hz以上的高频部分占比迅速减小；3)从速度谱看，谱幅值相对较大的区段则随着Tavg的增大向长周期段平移，同样以Tavg=2 s为界，越大长周期成分越丰富，速度反应谱峰值2 s后基本不断向右移动。可见，Tavg=2 s界限区分明显，可作为长周期分量提取的频谱指标。

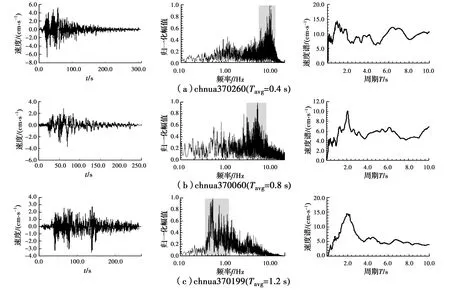
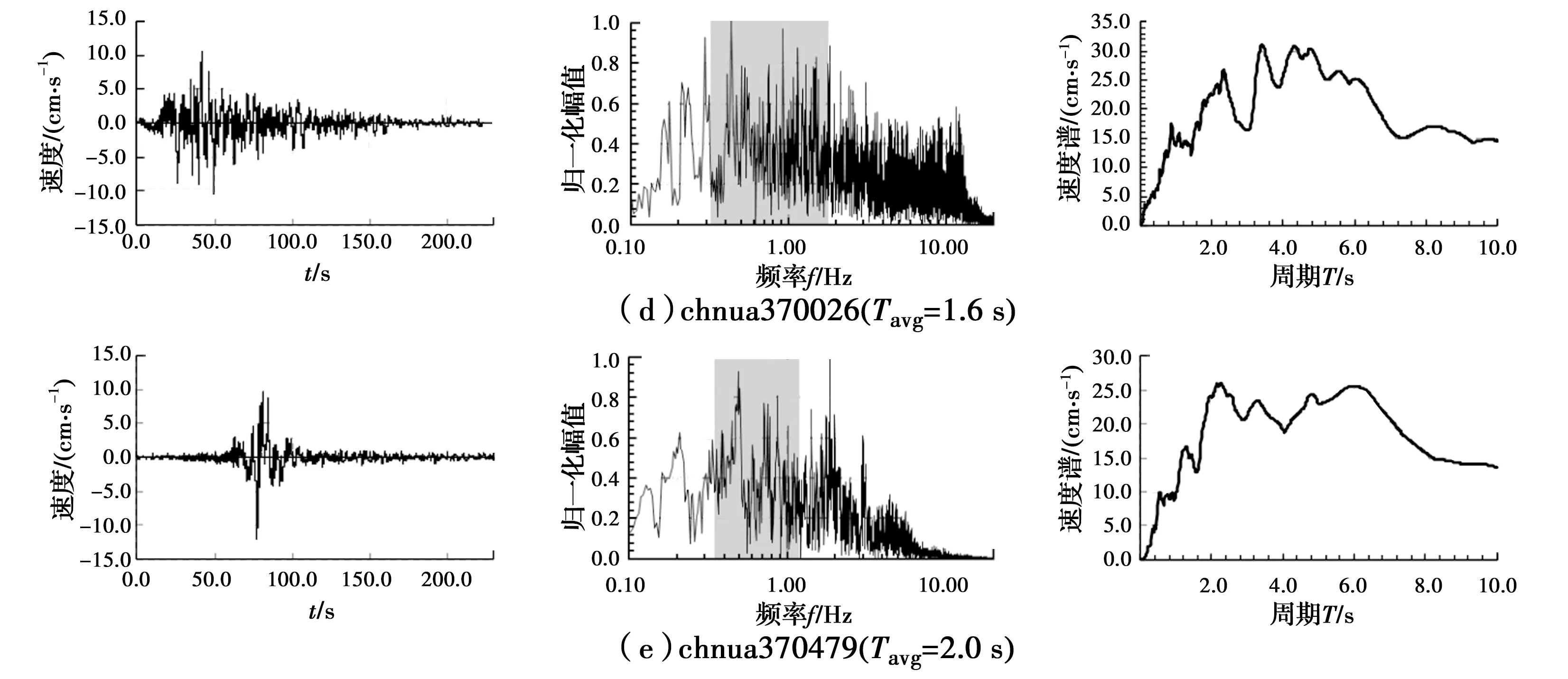
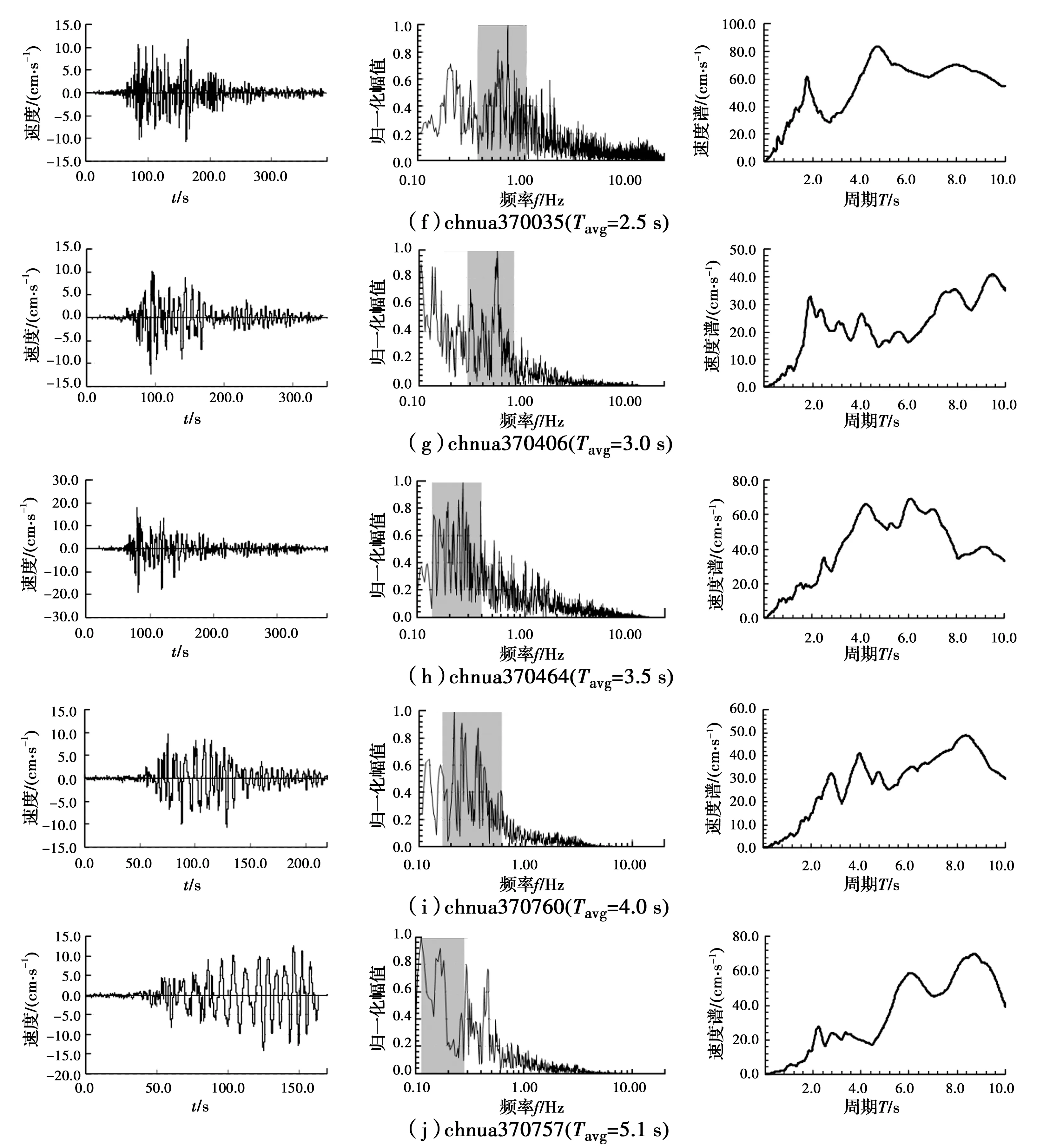
图2 地震记录速度时程、归一化傅里叶谱和速度谱伴随Tavg的变化特征Fig.2 Variation characteristics of velocity time-history, normalized Fourier spectrum and velocity spectrum with vary Tavg

3 分量提取方法步骤

1)地震记录的提取。以汶川地震中的长周期地震动chnua370505为例，其加速度、速度、位移时程曲线见图3(a)，采用EMD方法的步骤对原始地震记录(Original)加速度时程分解，提取地震记录中的IMFs和残余分量(R)，提取的IMFs以I1、I2、I3…I12表示，见图3(b)，通过EMD的步骤可以知道，最终提取的IMFs和R均需符合EMD中的两个限制条件。

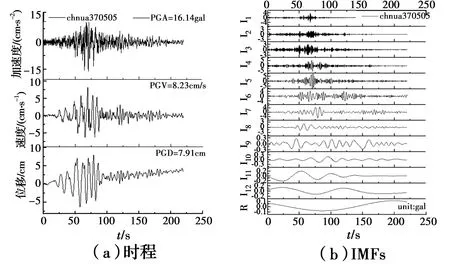
图3 chnua37050时程及IMF分量Fig.3 Time history and IMF components of chnua370505

2)地震动长、短周期分量的重构。基于地震动chnua370505的IMFs求解对应的Tavg值，如表1所示；由于地震记录周期10 s以后不确定性的存在，导致在限定周期范围时仅取值10以内。以Tavg=2 s为界，将提取的2 s及以上的IMFs与R叠加重构为长周期分量(long period components, LPC)，小于2 s的IMFs重新组合为短周期分量(short period components, SPC)。表1显示：地震动的前4个IMFs的Tavg小于2 s，叠加组合为初始短周期分量，后面7个IMFs与R的Tavg大于2 s，重新组合为初始长周期分量，组合后的长、短周期分量时程见图4。根据EMD中地震信号重构公式(4)可知，重构后的加速度LPC与SPC应符合式(6)、式(7)的范式，形成的长、短周期分量与IMFs叠加的误差应在可接受范围内，式中k表示Tavg≤2 s的IMFs最大分量的下标。进一步对加速度分量积分，得到速度分量(图4)，为后续校正做准备。

(6)

(7)

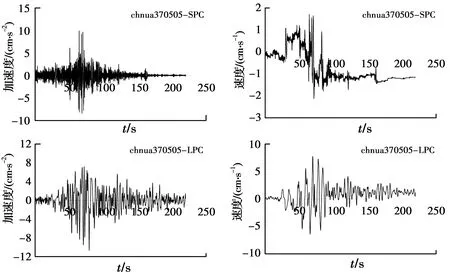
图4 叠加后的加速度与速度分量Fig.4 Acceleration and velocity components after superposition

表1 chnua370505的IMFs对应的Tavg值Table 1 Tavg values corresponding to IMFs of chnua370505 s

3)分量基线漂移的消除。由图4的加速度与速度时程曲线可看出，重新组合的加速度分量时程无基线漂移，速度时程偏移明显。与原始地震动进行基线校正同样的目的，为了消除基线偏移对信号处理结果造成的干扰，保证分析结果的有效性，对重构后的加速度分量时程进行基线校正与滤波，形成校正后最终的加速度长周期分量与短周期分量，积分得到速度分量时程，消除基线漂移后的加速度、速度时程如图5所示。可以看出，基线校正对基线漂移的控制效果明显，速度分量时程的偏向大幅度减小，校正后的地震动分量能更好地代表实际地震动，可将地震动中的干扰因素最大程度地排除。

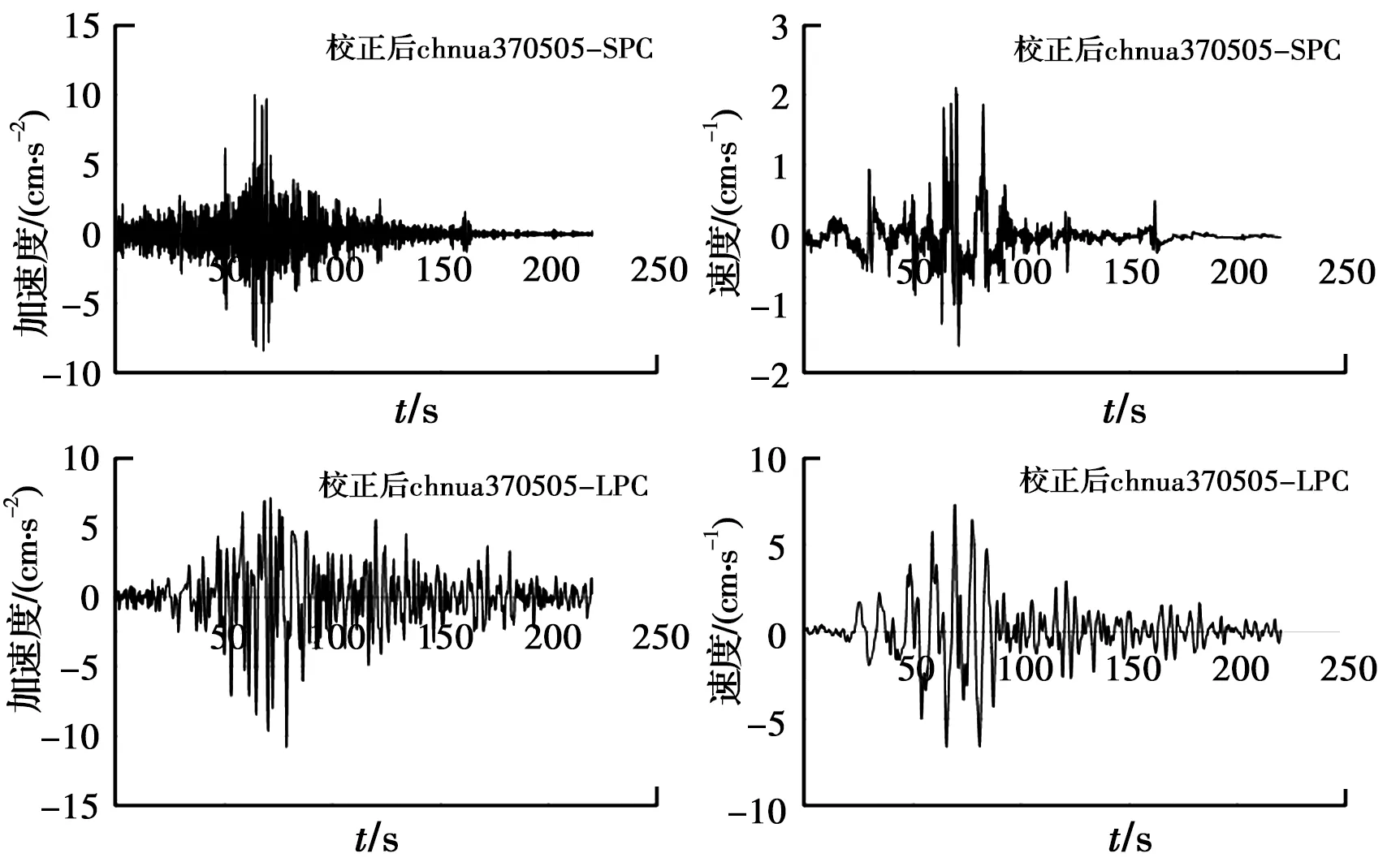
图5 消除基线漂移的分量时程Fig.5 Component time history by eliminating baseline drift

4 长周期分量提取方法的有效性验证

4.1 地震波分量提取

以Chi-Chi地震中的地震记录ILA056-NS与TCU052-EW验证本文提出的提取方法的有效性。基于地震动记录的波形特点，王博等[13]将长周期地震动分为远场长周期地震动与近断层长周期地震动，从而可将ILA056-NS归类于前者，而TCU052-EW归类于后者；图6展示了两条地震记录的加速度与速度时程与其分量。可以看出：在原始记录中，基线漂移均未在加速度时程和速度时程中出现；观察加速度、速度分量的时程，基线偏移在加速度分量中没有出现，而速度分量偏移明显，是对上述分量提取方法二次校正的必要性的进一步确认。

图6 ILA056-NS 、TCU052-EW原地震记录及分量加速度和速度时程Fig.6 Acceleration and velocity time history of original seismic records (ILA056-NS 、TCU052-EW)and their components

4.2 原地震记录与其长周期分量相关性

验证提取分量的代表性和有效性，可以分析地震记录分量与原地震动的相关性。图4与图6显示，未校正的地震记录分量速度时程存在明显基线偏移；对比图5中校正后的分量速度时程，漂移消除效果较好。分析校正后的地震动分量速度时程与原地震动的相关性更可靠。从图7可看出相关性趋势：从地震记录的波形判断，两条地震记录校正后的LPC与原始地震动吻合较好，SPC与原地震动吻合较差，说明长周期地震动的LPC在很大程度上能够代表长周期地震动，而SPC则不能代表，表明上述提取分量的代表性与有效性，同时，表2中的相关性系数计算值也更进一步说明基于速度的LPC与长周期地震动速度时程的相关性更好。

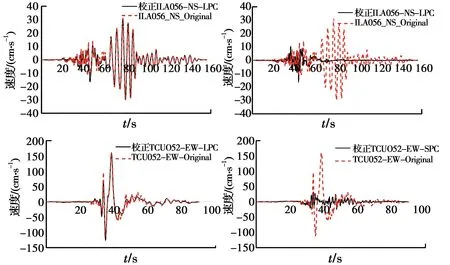
图7 原地震记录与重构校正后分量的相关性Fig.7 Correlation between original seismic records and their reconstructed and baseline drift corrected components

4.3 地震地面运动反应谱的离散性分析

分量提取方法的适用性已经通过相关性验证做出说明，进一步可以通过地震记录分解前后反应谱的变化来验证。在设计反应谱准确估计的影响原因中，基于统计分析的地震反应谱的离散性不可忽视，且加速度反应谱长周期段的离散性更加突出[3]。图8对比了两条原始地震记录与其长、短周期分量的反应谱的吻合程度，ILA056-NS反应谱与长周期分量反应谱在长周期段整体吻合较好，TCU052-EW吻合稍差，短周期分量与两条原地震记录在短周期段吻合，长周期段偏差显著。此种差异，是由远场长周期地震动与近断层长周期地震动的长周期分量更丰富的分布特征决定的。徐龙军等[3]以离散性系数k来评价地震反应谱的离散性，其计算公式见式(8)。借用参数k来评估LPC反应谱与原始地震记录反应谱的离散性。离散系数k与离散性是正相关关系。基于两条地震记录与其分量反应谱，计算得到k，见表3。从表中k的值可判断，长周期分量与原长周期地震动的离散性较小，短周期分量与原长周期地震动的离散性较大，同图8结果一致。

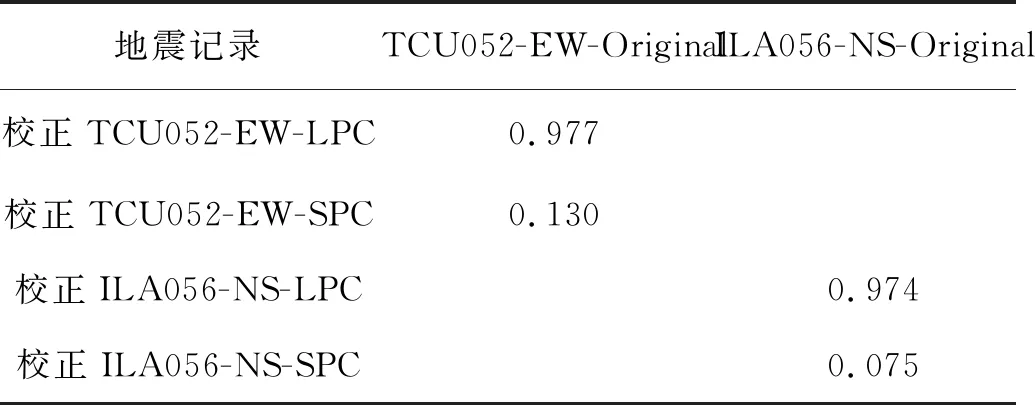
表2 原地震记录与分量速度时程的相关性系数Table 2 Correlation coefficients of velocity time history of original seismic records and their components

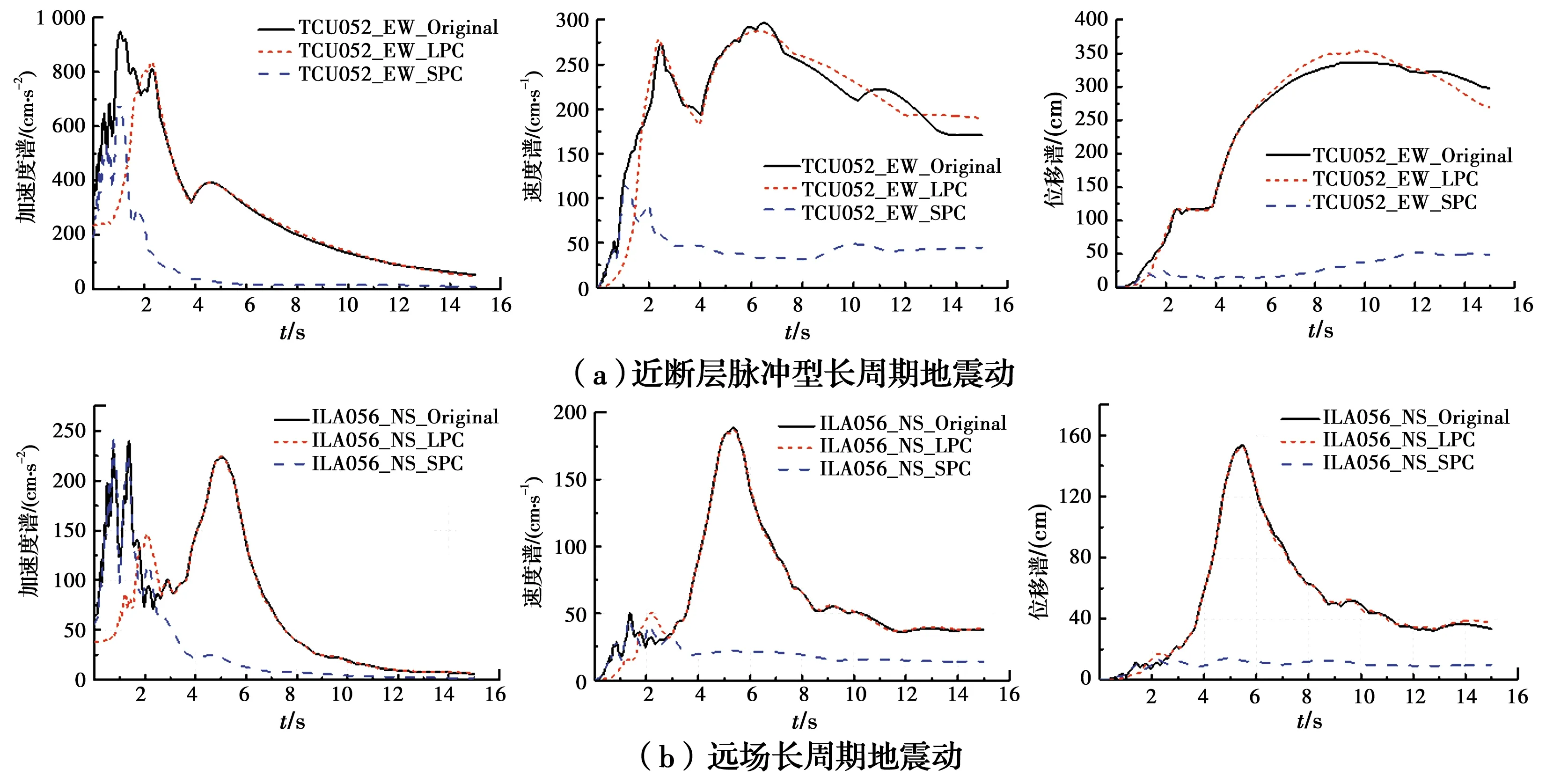
图8 地震记录(ILA056-NS、TCU052-EW)及其长、短周期分量反应谱Fig.8 Seismic records(ILA056-NS、TCU052-EW)and their long , short periodic components response spectra

(8)

式中：S1T为原地震动在周期T时的反应谱值；S2T为各分量在周期T时的反应谱值；ΔT为反应谱的计算周期间距，取为0.02；Ttol为反应谱的计算最大周期，取15 s。

表3 长、短周期分量与原地震记录反应谱的离散性系数Table 3 Discretization coefficients of response spectra of original ground motions and their long, short period components

5 不同分量提取方法的结果对比

Baker[6]对脉冲型地震动进行分量分离时采用了基于小波分析的分量提取方法，小波分析过程中，母波选择多贝西四阶小波，将地震记录分解为15个分量，并计算每个分量的Tavg值,其值大于2.0 s的重构为长周期分量，小于2 s的组合为短周期分量；Farid Ghahari等[8]采用滑动平均滤波方法提取脉冲型分量。其步骤：1)用短时傅里叶变换计算速度时程的卓越周期Tp；2)采用式(9)结合卓越周期Tp得到参数m的值，式(9)中参数α采用文献[8]中的经验取值0.25，dt为地震记录采样点的时间间隔；3)以m值代入式(10)计算截止频率fc，fc取倒数得到截止周期Tc(式(11))；4)利用Tc，结合滑动平均滤波来识别长、短周期分量。将上述两种方法提取的分量反应谱与以EMD方法提取的分量转换反应谱一起与原地震动的反应谱进行吻合性对比，由图9可以看出，基于EMD的长周期分量提取方法提取的长周期分量反应谱在长周期段与原地震动反应谱整体上吻合较好；与基于小波分析的方法相比，在ILA056-NS中，长周期段具有相近的效果，在TCU052-EW中，本文的方法提取效果更好；而与基于滑动平均滤波的方法比，本文方法提取的长周期分量均能更好地预测地震记录和反应谱的趋势。

(9)

(10)

(11)

图9 EMD、MA、Wavelet分量提取结果对比Fig.9 Comparison of component extraction results by EMD、MA、Wavelet

6 结论

研究了基于EMD的长周期地震动分量提取方法，对方法的有效性进行了分析，并与以往的分量提取方法进行对比，主要结论包括：

1)Tavg大于2 s的长周期成分在长周期地震动中起着至关重要的作用。由于对于大多数长周期地震记录，周期高于2 s的速度谱振幅通常比周期低于2 s的速度谱振幅更具优势，2 s以下基本不再出现峰值点。归一化傅里叶谱的频率成分偏向于低频，通过地震动特性分析确定了分量分离的周期参数(Tavg)及取值，该结果被建议作为长周期地震动识别程序中的关键参数。

2)采用经验模态分解方法，将地震动波分解成IMFs；结合截止周期Tavg=2 s，将相应的IMFs分别重组为长周期分量、短周期分量并校正，进而建立地震动长周期分量提取方法，并提出了分量提取实现的程序。

3)基于原地震动与长、短周期分量的相关性，地震动反应谱与长、短周期分量的反应谱的离散性对分量提取方法的有效性进行了验证，并将基于EMD的分量提取方法与基于小波、滑动平均滤波的方法进行了比较，验证了方法的合理性与有效性。提取的长周期分量是长周期地震动识别模型化的数据基础与参数指标来源。