四川省贪污罪量刑实证研究
樊祜玺,先德奇
(1.西南科技大学 四川绵阳 621010;2.西南医科大学 四川泸州 646000)
权力导致腐败,绝对权力导致绝对腐败[1]。作为最严重的贪污贿赂类犯罪之贪污罪,严重侵害了公共财产权和国家工作人员的廉洁性。惩治贪污腐败业已成为世界性难题,各个国家都应当进行有效监管,促进惩治贪污腐败的经验交流[2]。近年来,我国贪污罪的发生严重影响了党和政府机体的健康与活力,必须严厉予以打击。而贪污罪的量刑问题是打击和预防贪污犯罪行为的关键之一,从1997 年《刑法》贪污罪量刑的“犯罪数额中心论”建构,到2014 年《刑法修正案九》(以下简称《修正案九》)关于贪污罪量刑的“犯罪数额+情节”改变,再到2016年《最高人民法院、最高人民检察院关于办理贪污贿赂刑事案件适用法律若干问题的解释》(以下简称《解释》)对贪污罪犯罪数额、情节的细化,学者们在理论和实证方面均有较为详细的研究,主要反映出的是数额论量刑规则下的司法适用偏轻,或者在审判地域和犯罪数额阶梯等方面量刑畸轻畸重现象。在“犯罪数额+情节”论量刑规则下,司法适用相对合理,但也有实证研究指出,罚金刑适用较之旧量刑规则更趋于轻缓。整体而言,贪污罪在量刑中仍存在一定程度的不足,特别是各地法院不易统一把握特定情节的量刑比重和幅度,需要在从严惩处贪污贿赂犯罪的刑事政策指导下,对这些关键量刑情节的比重进行重新分配,均衡不同特定情节对量刑的影响,以保障刑罚目的的实现。为此,本文采用实证分析的方式,对四川省贪污罪一审判决书中所展现的贪污罪量刑现状、特征及规律予以分析和总结,探寻出特定情节在贪污罪量刑中的均衡关系,以期为审判人员提供实际参考,切实将贪污罪量刑推向均衡化的轨道上,更好地打击和预防贪污犯罪。
一、样本的选择及实证研究方法
(一)样本来源及研究对象
在中国裁判文书网以“刑事案件”为案件类型,以“判决书”为文书类型,以“贪污罪”为案由,以“一审”为审判程序,以“四川省”为法院地域,以“2012 年1 月1 日至2018 年5 月1 日”为判决日期,选择全部法院层级,共检索到577 份判决书①。其中有两份判决书不符合日期条件,本文将其从样本中删除。由于存在共同犯罪,为了使实证分析客观科学,本文以判决书所记载的每一个被告人作为一个测量单位进行数据的整理录入[3],共计924 个被告人构成贪污罪。其中,免于刑事处罚123 例,不在贪污罪量刑研究范围内,本文将其删除。所以,本文将构成贪污罪的剩余801 个被告人作为研究对象。
(二)实证研究方法
根据《修正案九》及《解释》,结合《刑法》关于贪污罪的基本理论,本文设置了贪污罪的23 个变量:犯罪所属市、贪污是否最基层、犯罪主体类型、利用职务便利类型、犯罪手段、犯罪对象、贪污数额、案发原因、是否共同犯罪、共同犯罪人数、主从犯划分、是否存在犯罪未遂、犯罪持续时间②、是否退赃、是否自首、是否坦白、是否立功、主刑刑种、刑期、是否缓刑、缓刑考验期、并处罚金或没收财产数额、判决时间。将801个贪污罪被告人的量刑按照以上变量进行归纳整理,运用spss21.0统计软件进行统计分析,综合运用统计描述、t检验、卡方检验、双变量相关分析、多元线性回归分析、Logistic回归分析等统计学方法,对自由刑刑期、财产刑数额以及缓刑适用进行整体分析,从而构建出贪污罪的量刑基础模型。
二、四川省贪污罪量刑基本情况
(一)自由刑适用情况
在四川省801 个贪污罪被告人中,被判处拘役25 人,占总案例数的3.12%,剩余776 人均为有期徒刑,占总案例数的96.88%。由于拘役刑种所占比重较小,为了更加全面地展现四川省贪污罪的刑期长短情况,本文将拘役刑期和有期徒刑刑期数据合并进行统一分析,结果发现(见表1),801个被告人贪污罪量刑均值为28.57个月,中值③为24个月,众数④为12个月,最低刑期为2个月,最高刑期为168 个月。在贪污罪第一档刑期3 年以下有期徒刑或拘役中,选择在法定刑中线18 个月以下进行量刑的案例(包含本数)有379例,占一档刑案例总数的57.16%,占全部案例总数的47.32%,在贪污罪第二档刑期3年以上10年以下有期徒刑中,选择在法定刑中线79个月以下量刑的案例有100例,占二档刑案例总数的79.37%,占全部案例总数的12.48%。从以上分析可知,四川省贪污罪量刑刑期整体偏低,无论是在第一档刑期还是第二档刑期中,选择法定刑中线以下量刑的法官占了较大比例,量刑司法实践表现与从严惩治贪污贿赂犯罪的刑事政策有较大出入。

表1 刑期分段频率分布
(二)缓刑适用情况
在四川省801 个贪污罪被告人中,有465 人适用缓刑,占总人数的58.05%,占第一档刑期量刑人数的70.14%。是否缓刑除了要依照《刑法修正案(八)》的硬性规定外,法官是最后决定者。将不符合《刑法修正案(八)》规定缓刑条件的案例纳入我们的考虑中,结合实际缓刑所占比例,我们不难发现只要是符合《刑法修正案(八)》规定缓刑条件的案例,法官在自由裁量方面几乎都决定适用缓刑。对缓刑考验期进行统计描述发现,四川省贪污罪缓刑考验期均值为26.39个月,中值为24个月,众数为12 个月,最低缓刑考验期为5 个月,最高缓刑考验期为60 个月。其中缓刑考验期19~24个月、25~36个月(见表2)这两个段较其他各段占比较大,占所有缓刑案件的49.03%,与缓刑考验期均值较为接近。因此,从四川省贪污罪缓刑适用表现来看,缓刑适用率过高,与从严惩处贪污贿赂行为的刑事政策相违背,但是从缓刑考验期适用来看,缓刑考验期适用较为均衡。

表2 缓刑考验期分段频率分布
(三)财产刑适用情况
贪污罪的财产刑包括罚金和没收财产,为了使统计更加显著,本文对罚金和没收财产统一进行数据处理。在四川省801 个贪污罪被告人中,有570 个被告人适用了财产刑,财产刑适用率为71.16%,财产刑数额均值为14.4746 万元,中值为10 万元,众数为10 万元,标准差⑥为12.64327 万元,财产刑数额最小值为1万元,最大值为150万元,说明财产刑数额离散程度较小,分布趋向于正态分布,财产刑数额较为均衡,但存在个别财产刑处罚畸重,其中财产刑数额在10 万元以下(包含本数)的案例有382件,占处以财产刑总案例的67.02%(见表3)。根据《修正案九》及两高《解释》中的规定,对贪污罪、受贿罪量刑时应当并处罚金,其中最低10 万元,最高到犯罪数额的两倍以上至没收财产[4]。由此可见,财产刑数额集中值较低,财产刑处罚整体偏轻。

表3 财产刑数额分段频率分布
三、四川省贪污罪量刑特征考察
(一)贪污罪有期徒刑量刑特征考察
1.犯罪持续时间对有期徒刑量刑的影响。将犯罪持续时间与刑期做相关分析得到,犯罪持续时间与刑期的Pearson 相关系数为-0.134,P 值=0.002〈0.01,可以认为犯罪时间与刑期存在负相关性,犯罪持续时间越长,刑期越短。一种可能是本文设置的犯罪持续时间是通过判决时间和犯罪开始时间相减得到,这说明在未被刑事追究之前,发生越早的贪污罪,量刑可能会越轻,很大可能与刑罚预防刑的立法设置有关。距离犯罪结束时间越长,人身危险性越低,再犯可能性越小,预防刑刑期越短,总的刑期也就越短。另一种可能原因在于,“理论上一般认为量刑是一个既要考虑报应与预防,又需权衡各种因素的复杂活动。但实证研究的结论却表明,刑罚裁量是一个以确定行为严重性为导向,仅对有限变量进行笼统评估的过程,量刑呈现出简洁化特征。”[5]本文的双变量相关分析比实务处理更简洁,可能忽略了其他变量对量刑的影响,导致其他变量的相关性错误。因此需要在下面对其他变量的相关性分析中探索,看是否有相反表现的变量,以对两种假设进行验证。
2.贪污金额对有期徒刑量刑的影响。贪污金额与刑期长短显著相关,金额越多,刑期越长。将法院认定的贪污金额与刑期做方差分析得到,统计量F=231.052,P〈0.001,可以认为金额与刑期在α=0.01 的检验水准下存在线性回归关系。回归方程回归系数为0.172,可以认定贪污金额与刑期存在较强相关,贪污金额对刑期长短有着重要影响。
3.是否特定款物对有期徒刑量刑的影响。是否特定款物与刑期有相关关系,贪污特定款物刑期反而比较低。在四川省贪污罪案例中,特定款物⑦所占案例的刑期均值为22.61 个月,中值为15个月,众数为12 个月。非特定款物案例中刑期均值为32.56 个月,中值为26.00 个月,众数为36 个月。可以看出,贪污特定款物所获刑期竟然比贪污非特定款物所获刑期要低,从侧面一定程度可以反映出法院在量刑时可能较少考虑量刑情节中的特定款物。还有,本文所用研究对象横跨了《修正案九》和《解释》的实施日期,也有可能是先前贪污罪量刑犯罪数额中心论向“数额+情节”中心论转向过程中遗留的问题。笔者进一步将是否特定款物与刑期做相关t 检验得到,统计量t=3.628,自由度v=363,P〈0.001,在α=0.05 的检验水准下有统计学意义,可以认为特定款物与非特定款物案例的刑期长短不同,是否特定款物与刑期长短之间有相关关系。前述是否特定款物反映出的均值问题要在《解释》的指导下,在进行有期徒刑量刑模型构建时予以修正,以更好契合《修正案九》和《解释》要求的贪污罪量刑“数额+情节”论。
(二)贪污罪缓刑适用特征考察
1.犯罪持续时间对缓刑的影响。犯罪持续时间与缓刑成负相关,犯罪持续时间越长缓刑适用概率越小。统计结果显示,缓刑组犯罪持续时间均值为5.17 年,非缓刑组犯罪持续时间均值为5.62 年,差值为0.45 年。另外对犯罪持续时间和是否缓刑做t 检验得到,统计量t=2.007,P=0.045〈0.05,进一步证明犯罪持续时间与缓刑在统计学上存在相关关系。缓刑本应面向人身危险性小、再犯可能小的被告人。在犯罪持续时间对刑期的影响分析中,我们得出了两个假设:一个是犯罪持续时间长、人身危险性小,预防刑会减少的假设;另一个是实证研究导致量刑特征简洁化的假设,由此看来,双变量相反的相关表现证明第二种假设成立。因此,犯罪持续时间对刑期和缓刑的统计学影响对实务来说并无相应参考意义,应予以舍弃。
2.其他变量对缓刑的影响。是否坦白、是否自首、是否退赃等因素经过相关性分析发现对是否缓刑有较强影响,这也与缓刑适用的实践考量情节达成一致,在此就不再赘述,相关影响程度在缓刑适用模型构建时予以考量。
(三)贪污罪财产刑适用特征考察
1.是否共同犯罪对财产刑数额的影响。非共同犯罪财产刑数额高于共同犯罪财产刑数额。共同犯罪组财产刑数额均值为13.73 万元,非共同犯罪财产刑数额均值为17.35 万元,在统计学上有明显差异(F=8.394,P=0.004〈0.05),无论从司法理论还是实践层面来说,共同犯罪危害都要比普通犯罪要大,共同犯罪财产刑处罚也应该比普通犯罪要重。此处出现有违与学界和实务界共识的结论,笔者认为是样本选择偏差造成的,前面提到笔者将一例共同犯罪判决书中的每一被告人都当做一个研究对象,此处研究的财产刑数额也是每位被告人被处罚的数额。贪污罪的处罚严重与否又与贪污金额有密切关系,金额越大,处罚越重,总的贪污金额分担到每个被告人身上就会造成共同犯罪中单个被告人处罚整体较普通犯罪轻。
2.贪污金额对财产刑数额的影响。法院认定的贪污金额与财产刑数额存在较强直线相关,金额越大,罚金数额越高。两者Pearson相关系数为0.560,P〈0.001,回归方程的贪污金额回归系数b=0.086。
3.犯罪持续时间对财产刑数额的影响。犯罪持续时间与财产刑数额几乎不存在相关性。两者Pearson相关系数为0.055,P=0.196〉0.05。
4.刑期长短对财产刑数额的影响。判处刑期长短与财产刑数额存在明显直线相关,刑期越长,财产刑数额越高。两者Pearson相关系数为0.663,P〈0.001,回归方程刑期回归系数b=0.384。
贪污是否特定款物、是否退赃、是否悔罪等因素,经相关性分析发现P值均大于0.05,其对财产刑数额均明显无相关影响。
四、四川省贪污罪量刑基准模型的构建
通过对四川省贪污罪量刑基本特征的分析发现,无论是刑期量刑、财产刑量刑,还是缓刑量刑都呈现出较强的规律性。为了使贪污罪量刑更加均衡、公正,笔者进一步探索这种规律,并试图将这种规律以方程式固定下来,从而构建出贪污罪量刑的基准模型。基准模型中最重要的就是变量的选取,结合前文分析,笔者将与量刑存在相关关系的变量作为自变量代入模型中进行筛选,从而得出较为准确的量刑方程式。法官在处理贪污罪案件时,就可以依据方程式得出个案的量刑值,这个值不一定就是宣告刑,而是起到基准线的作用,供法官在此基准线上下自由裁量,避免量刑畸轻畸重。如果缺乏这一条基准线,就没有参照物引导法官的量刑行为,刑罚权就存在失控的可能[6]。另外,模型所使用的数据均来自真实的案例数据,通过前文分析我们了解到实践中刑期裁量过低,缓刑适用率过高,不符合从严惩治贪污犯罪行为的刑事政策。因此,该量刑基准模型还需要进一步修正,以期符合宽严相济的刑事政策。
(一)有期徒刑刑期基准模型的构建、修正及运用
在四川省贪污罪801 个被告人中,有25 人被处以拘役刑期,776 人被处以有期徒刑。因拘役和有期徒刑性质不同,适用条件有所差异,为了使刑期量刑基准模型更加符合实际,这里仅把被处以有期徒刑的776 名被告人当做构建模型的实际研究对象。通过前文分析可知,776 名研究对象刑期范围涉及贪污罪的第一档刑期、第二档刑期以及第三档刑期,贪污罪档期的确定由贪污数额和情节决定,模型的构建过程中已经把贪污数额和相应情节纳入统计考虑之中,模型中已经包含档期的区分,所以在此就不分别单独建模了。贪污罪存在共同犯罪问题,为了使模型更加科学笔者将样本区分为共同犯罪和非共同犯罪两个部分,分别建立贪污罪有期徒刑的量刑模型。
1.有期徒刑刑期基准模型的构建。
(1)非共同犯罪案件的有期徒刑刑期基准模型的构建。将法院认定的贪污数额、是否基层贪污、贪污是否特定款物、是否退赃、是否认罪悔罪、是否坦白、是否自首、是否立功作为自变量,将有期徒刑刑期作为因变量代入回归模型中。初步回归模型显示(见表5)贪污金额、是否退赃、是否基层贪污作为有统计学意义(P〈0.05)的自变量留在了回归方程中,但是我们发现是否基层贪污这一自变量的回归系数为负值,即是否基层贪污取值越大,则刑期就会相应减少,在进行数据数值化的过程中,非基层贪污赋值为1,基层贪污赋值为2,因此当是基层贪污的时候,即取值为2的时候刑期减少了。通过统计数据得知,发生在基层贪污的犯罪对象大多数是补偿款这类的特定款物,根据《解释》的规定,犯罪对象为特定款物的认为是贪污的一种加重情节,刑期应该增加,不应减少,在之前分析量刑特征的时候我们也发现了是否特定款物与刑期负相关,与《解释》的司法目标相反,为了保证量刑的准确,应将此类变量予以剔除。经过对剩余自变量进行多次回归分析并考虑二分类变量可能的共线性筛选,贪污金额与是否退赃这两个自变量最终留在了回归模型中(见表6),所以非共同犯罪案件的有期徒刑量刑模型为:Y=82.891+0.15*X1-28.942*X2(其中Y 表示贪污罪的量刑刑期,单位为月;X1 表示贪污金额,单位为万元;X2 表示是否退赃,退赃取值2,未退赃取值1)。

表5 非共同犯罪案件有期徒刑刑期初步回归模型

表6 非共同犯罪案件有期徒刑刑期回归模型
(2)共同犯罪案件的有期徒刑刑期基准模型的构建。将个人贪污金额、主从犯、是否基层贪污、贪污是否特定款物、是否退赃、是否认罪悔罪、是否坦白、是否自首、是否立功作为自变量,将有期徒刑刑期作为因变量代入回归模型中。同非共同犯罪案件有期徒刑刑期量刑模型构建步骤,个人贪污金额、主从犯、是否坦白三个自变量留在了回归模型中(见表7)。所以共同犯罪案件的有期徒刑量刑模型为:Y=39.202+0.806*X1-3.091*X2-6.039*X3(其中Y表示贪污罪的量刑刑期,单位为月;X1表示个人贪污金额,单位为万元;X2表示主从犯,主犯取值为1,未区分主从犯取值为2,从犯取值为3;X3表示是否坦白,坦白取值为2,未坦白取值为1)。
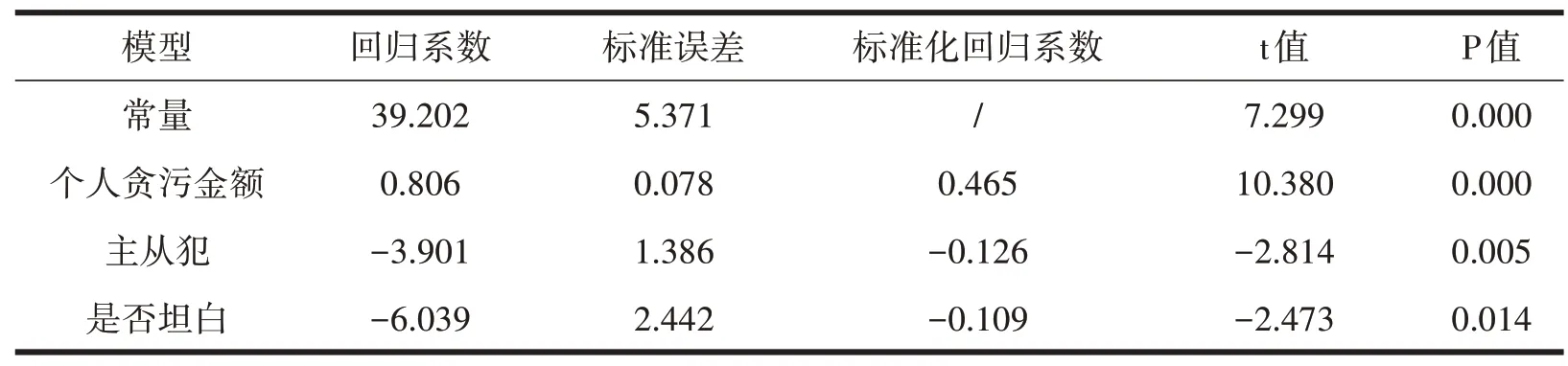
表7 共同犯罪案件有期徒刑刑期回归模型
2.有期徒刑刑期基准模型的修正。前文提到,所有的统计数据均来自于贪污罪实务案例,经统计发现(见表2),贪污罪实务案例的量刑过轻,大部分宣告刑都低于法定刑中线,不符合从严惩治贪污犯罪行为刑事政策的要求。裸刑均值普遍低于法定刑中线已是既成事实,即使有理由改变也应渐进而行[7]。所以笔者将贪污罪刑期均值定量为每一档刑期法定刑中线值来修正刑期量刑模型。本文研究数据涉及贪污罪三档刑期,每档刑期的法定刑中线值分别为18 个月、78.5个月、180 个月⑧。修正等式可列为:B=(M*N)/A(B 为每档实际刑期应乘的修正倍数;M 为每档刑期的法定刑中线值,单位为月;N 为每档刑期的实际案件数;A 为每档所有刑期的合计值)。进行修正时按照每档刑期分别进行,当出现M*N 的值小于A 值时,则证明该档期不用修正,符合宽严相济的刑事政策。另外当修正后的刑期值超出了所在的档期最大值时,则取档期最大值为修正后的刑期值。
非共同犯罪案件的有期徒刑量刑修正模型为:Y=93.569+0.177*X1-34.145*X2(其中Y 表示贪污罪的量刑刑期,单位为月;X1 表示贪污金额,单位为万元;X2 表示是否退赃,退赃取值2,未退赃取值1)(见表8)。

表8 非共同犯罪案件有期徒刑刑期修正模型
共同犯罪案件有期徒刑量刑修正模型为:Y=45.02+0.943*X1-4.726*X2-7.883*X3(其中Y表示贪污罪的量刑刑期,单位为月;X1 表示个人贪污金额,单位为万元;X2 表示主从犯,主犯取值为1,未区分主从犯取值为2,从犯取值为3;X3表示是否坦白,坦白取值为2,未坦白取值为1)(见表9)。

表9 共同犯罪案件有期徒刑刑期修正模型
3.有期徒刑刑期基准模型的运用。由于考虑到实证研究无法把所有的可能影响量刑的情节纳入到模型中,所以不可避免的会导致模型量刑的简洁化,所有必要在此对模型的运用做一个说明。首先,有期徒刑刑期的基准模型仅是给法官提供量刑参照的作用,并不能代替法官裁量的过程。其次,“法律规定每个量刑幅度内的数额范围及相对应的刑罚范围,言下之意,一定量的贪污数额大致对应着一定量的刑期。”[8]如果在使用模型过程中超出了贪污金额相对应的刑期范围,那么这个值在没有其他加重情节下,是不能作为量刑参考值的。最后,因为该量刑并未涉及无期徒刑案件,且10 年以上有期徒刑案件也涉及较少,所以在使用该模型时,对于一些极端案件,采用该模型进行参照时,应当慎重。
(二)财产刑数额基准模型的构建、修正及运用
1.财产刑数额基准模型的构建。《解释》第19 条对贪污罪的财产刑做了具体的规定⑨。由此可见财产刑数额范围和刑期范围是相匹配的,呈现一定的线性关系,而刑期长短又代表情节轻重,所以为了不重复评价贪污犯罪行为的量刑情节,仅将刑期作为自变量代入回归模型中进行构建财产刑数额模型。在《解释》实施之前,财产刑处罚数额没有明确标准参照,法官裁量范围大,所以为了使模型更加科学,笔者将构建模型所需要的研究对象限定在《解释》实施以后判决的贪污罪案件。将刑期作为自变量,财产刑数额作为因变量代入线性回归方程中,得到财产刑数额基准模型为:Y=2.012+0.569*X1(其中Y表示财产刑数额,单位为万元;X1表示刑期,单位为月)(见表10)。

表10 财产刑数额回归模型
2.财产刑数额基准模型的修正。刑罚具有威慑作用,财产刑处罚也不例外。贪贿犯罪作为贪利性犯罪,本质上不能脱离“贪利性”[9]。被告人不劳而获的逐利思想直接导致了贪污罪的发生,有效合理的运用财产刑,可以震慑犯罪分子的贪腐思想。由于刑罚本身的威慑力是抽象的,强加于罪犯,必须使其信服或不再质疑,刑罚忽轻忽重很可能导致公众对罪犯的情感从“谴责”到“同情”,会导致犯罪人及潜在犯罪人产生怀疑[9]。这种怀疑不仅会降低财产刑的震慑作用,而且还会直接浪费作用财产刑上的司法资源。所以财产刑处罚的数额标准要合理,过轻过重都不利于威慑贪腐分子。如前所述,目前司法实践对贪污罪财产刑数额处罚较轻,数额基本上选取固定在每档财产刑的最低值。白建军教授指出实务量刑过轻,即使加重也要循序渐进,不能一蹴而就。所以笔者决定采用修正后的刑期值代替实际刑期值来修正财产刑数额模型比较合理。修正后的财产刑数额模型为:Y=2.902+0.503*X1(其中Y表示财产刑数额,单位为万元;X1表示刑期,单位为月)(见表11)。又因为贪污罪财产刑属于应当并处刑罚,财产刑数额最低为10万元,该模型中最低财产刑数额为3.405 万元,所以应当进一步修正模型,将其最低值调成10 万元,得出最终财产刑数额修正模型为:Y=9.497+0.503*X1。

表11 财产刑数额修正模型
3.财产刑数额基准模型的运用。贪污罪的财产刑处罚属于限额制财产刑,使用模型值进行参考时,超出限额额度的值应当舍弃,是否取额度最高值为参考值还需要考量具体情节来进行确定。
(三)缓刑适用基准模型的构建、修正及运用
1.缓刑适用基准模型的构建。依据我国《刑法》第72条、第73条规定,缓刑是指被判处拘役、3年以下有期徒刑的犯罪人,由于犯罪情节较轻,有悔罪表现,没有再犯罪的危险,暂不执行刑罚对所居住的社区没有重大不良影响,就可以规定一定的考验期,暂缓刑罚的执行[10]。用一个公式表示就是,缓刑的适用条件=刑期条件+对象条件+实质条件[11]。刑期条件要求必须是被人民法院判处拘役、3 年以下有期徒刑的宣告刑;对象条件表现为应当适用与不应当适用的表述:对犯罪时不满18 周岁的犯罪分子、审判时怀孕的妇女以及已满75 周岁的老年人满足适用缓刑条件的应当适用缓刑,并且强调累犯与犯罪集团的首要分子不得适用缓刑,实质条件聚焦于轻型犯罪,即必须情节较轻,属于轻型刑事犯罪,有悔罪表现,不具有再犯可能性[11]。所以本文将所有符合缓刑刑期条件、实质条件的案件筛选出来,再剔除符合对象条件的案件,将剩余案件作为构建缓刑适用模型的研究对象。所以缓刑适用模型构建其实就是将符合缓刑条件的案件,通过对各种犯罪情节及犯罪后表现的量化把控来模拟法官裁量的过程。因此我们将可能影响缓刑适用的犯罪情节和犯罪后表现等变量纳入到回归模型的构建中,通过多次Logistic 回归分析进行自变量的筛选,最终得到缓刑适用的基准模型为:
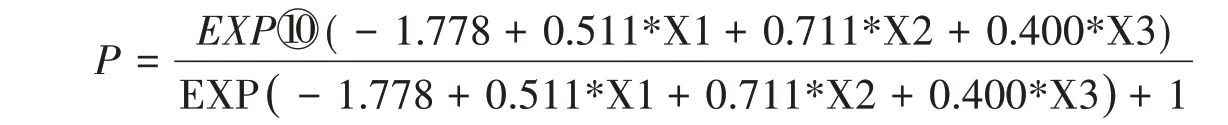
P(取值范围0~1)代表缓刑适用结果,当P≥0.5 时,应当适用缓刑,P〈0.5 时,不应适用缓刑。X1代表坦白,未坦白取数值1,坦白取数值2。X2 代表是否基层贪污,非基层贪污取数值1,基层贪污取数值2。X3代表是否自首,非自首取数值1,自首取数值2。
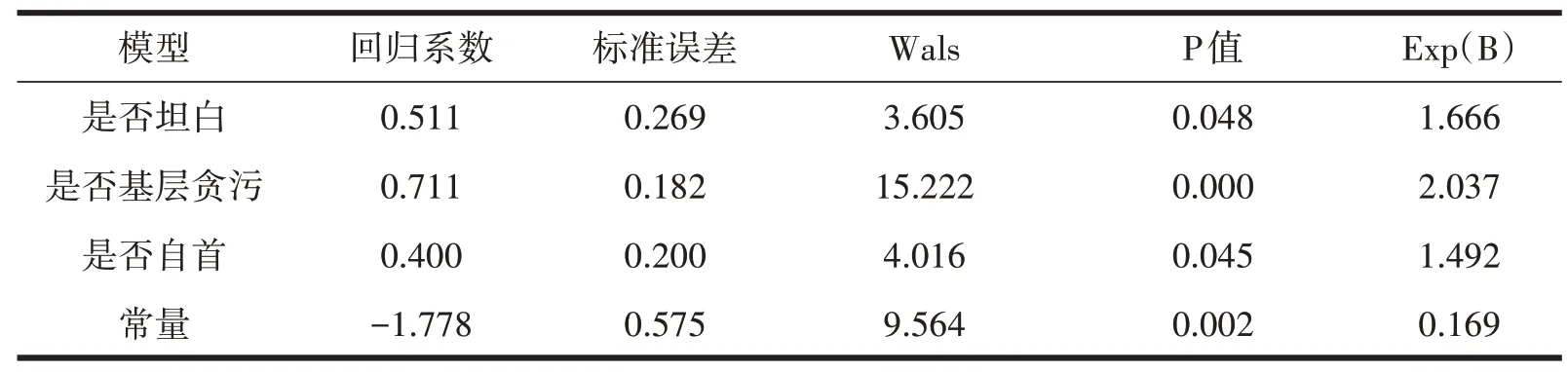
表12 缓刑适用基准模型
2.缓刑适用基准模型的修正和运用。通过表12我们可得知,影响缓刑的犯罪情节以及犯罪后表现经Logistic 回归模型多次筛选后,是否坦白、是否基层贪污、是否自首这三个变量具有统计学意义留在了缓刑模型中。模型表现从侧面反映出法官在衡量是否缓刑的过程中,较多的参考了是否坦白、是否基层贪污、是否自首这三个变量,对其他犯罪情节诸如是否共同犯罪、主从犯等可能未予评析,这也是导致缓刑率高的一个原因。从而也会不可避免地导致缓刑模型的简洁化,很可能在运用过程中产生偏差。笔者认为对缓刑模型修正应该人为加入可能遗漏的犯罪情节来全面评析被告人的再犯可能性和危险性。但由于笔者不能穷尽考虑这些情节因素对缓刑的影响,所以只能提高应当适用缓刑的P值来进行粗略修正。经过变量数值代入发现,缓刑模型的P值范围(近似范围)为:0.46≤P≤0.74,P 的中间值为0.60,如果是否缓刑P 值临界点取值0.60,此时实际缓刑率降低了近乎50%,为了与宽严相济的刑事政策相一致,笔者认为将缓刑率降低30%为宜,得出是否缓刑P的临界值为0.54,所以当P≥0.54时应当适用缓刑,P〈0.54时不应使用缓刑。另外考虑到该缓刑模型未能将其他可能因素纳入最终的考量范围,导致模型过于简洁化,缓刑适用模型结果作为法官是否缓刑的参考为宜,也可以作为衡量缓刑适用是否过于宽泛的衡量标准。
五、结论
从1997 年刑法到《修正案九》《解释》的实施,贪污罪经历了从立法完善向司法完善方向的转变。贪污罪刑罚方面的演进主要体现为刑罚配置与量刑标准、情节的改变,目的在于使得贪污罪的刑罚具有更强的适应性,满足打击贪污的现实需要[12]。《修正案九》和《解释》提高了贪污罪定罪与量刑金额,并且将相关情节纳入到贪污罪量刑占比中,以解决贪污罪司法适用不均、量刑畸轻畸重的困境。从实证研究结果来看,《修正案九》和《解释》实施以来,贪污罪量刑整体均衡,量刑力度平稳,但是这种均衡是低力度的均衡,打击效果没有明显提升。贪污罪被告人自由刑刑期大多数低于法定刑中线值,财产刑数额均接近于每档最低值,缓刑适用率较高。实证研究结果表明,《修正案九》和《解释》的司法实践效果并未达到刑事政策的目标要求。
在贪污罪自由刑方面,贪污罪“犯罪数额”论向“犯罪数额+情节”论转变过程中,司法审判人员不能很好把握特定情节对量刑的影响,例如是否特定款物对刑期的影响理应成正相关,但实证研究数据表明,当犯罪对象属于从重情节的特定款物时,自由刑刑期反而有一定程度的下降趋势。因此,应加强司法审判人员对特定情节的关注度,以及建立司法审判人员对把握特定情节在量刑中影响的培训制度,适当提高特定情节在量刑中的比重。
在贪污罪财产刑方面,“一直以来,理论界都在积极呼吁在贪污贿赂犯罪中增加以强制缴纳金钱为内容的罚金刑。”[13]《修正案九》增设了贪污贿赂犯罪的罚金刑,既是对理论界的回应,又符合经济快速发展下惩治贪污罪的需要。在这之后《解释》又规定了每档罚金、没收财产数额的范围。实证研究发现,在罚金和没收财产的选择上,司法审判人员并没有相应规定可循,出现了到底是适用罚金还是适用没收财产的困境。在财产刑数额的选择上,司法实践呈现出“低档低罚”,“高档也低罚”的局面。原因在于《解释》规定的数额范围差值较大并且不同档次之间存在数额交叉的问题,使得司法审判人员难以根据具体的情节选择合理的财产刑的数额。而笔者在前文建立的财产刑修正模型也只能一时性地解决财产刑数额偏低问题,要想从根本上解决问题,还得根据不同情节重新修正不同档次的财产刑数额范围。
在贪污罪缓刑适用方面,贪污罪实际缓刑率较高,在可以使用缓刑的情况下,法官基本上都选择了缓刑,对此,笔者认为应加强对审判人员从严惩治贪污犯罪政策思想的贯彻,从根本上使法官从严、慎重适用缓刑。
[注释]:
①所有判决书均于2018年5月在http://wenshu.court.gov.cn/网站收集。
②犯罪持续时间这里指从犯罪开始到判决日期所经历的时长。
③中值(又称中位数)是指将统计总体当中的各个变量值按大小顺序排列起来,形成一个数列,处于变量数列中间位置的变量值就称为中位数。
④众数(Mode)是指在统计分布上具有明显集中趋势点的数值,代表数据的一般水平,也是一组数据中出现次数最多的值。
⑤为了统计方便,79是贪污罪第二档刑期的法定刑中线的近似值,实际值为78.5。
⑥标准差(Standard Deviation),中文环境中又常称均方差,是离均差平方和的算术平均数的平方根,用σ 表示。在概率统计中最常使用作为统计分布程度上的测量。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
⑦我国在政府财政支出中特别设立民政事业费一项,包括救灾、抢险、防汛、优抚、扶贫、移民、救济款物,以便帮助人民群众战胜自然灾害,解决生活中的具体困难。
⑧这里笔者选取10年以上有期徒刑的最高刑期为20年。
⑨判处3年以下有期徒刑或者拘役的,应当并处10万元以上50万元以下的罚金;判处3年以上10年以下有期徒刑的,应当并处20万元以上犯罪数额二倍以下的罚金或者没收财产;判处10年以上有期徒刑或者无期徒刑的,应当并处50万元以上犯罪数额二倍以下的罚金或者没收财产。
⑩高等数学里以自然常数e为底的指数函数。

