一种安全高效的VANET 无证书聚合签名改进方案*

久美草，王 迪，刘芳芳，芦殿军

（青海师范大学 数学与统计学院，青海 西宁 810008）

0 引言

智能交通系统利用传感、控制、通信和数据分析等技术来提供创新性的服务，可以有效解决传统交通系统中固有的与交通相关的问题。近年来，配备有称为车载单元（On Board Units，OBU）的通信设备的车辆正在出现，且在很多路边和十字路口部署了路边单元（Road Side Units，RSU），以实现车辆和基础设施间的通信。这种模式创新了一种自组织网络，称为车载自组织网（Vehicular Ad-hoc Network，VANET）。如图1 所示，一般来说，VANET 由一个可信机构（Trusted Authority，TA）、安装了OBU 的车辆和RSU 组成。车辆之间以及RSU 和OBU 之间的通信利用DSRC 协议[1]实现；TA、RSU 和应用服务器（Applications Servers，AS）之间利用安全的有线信道[2]进行通信。根据VANET 的需求，每个OBU 能在100～300 ms[3]内频繁广播与交通相关的消息。RSU 可以从OBU 收集这些数据，并验证其真实性和完整性，最后将有效的数据传输给AS 进行分析。

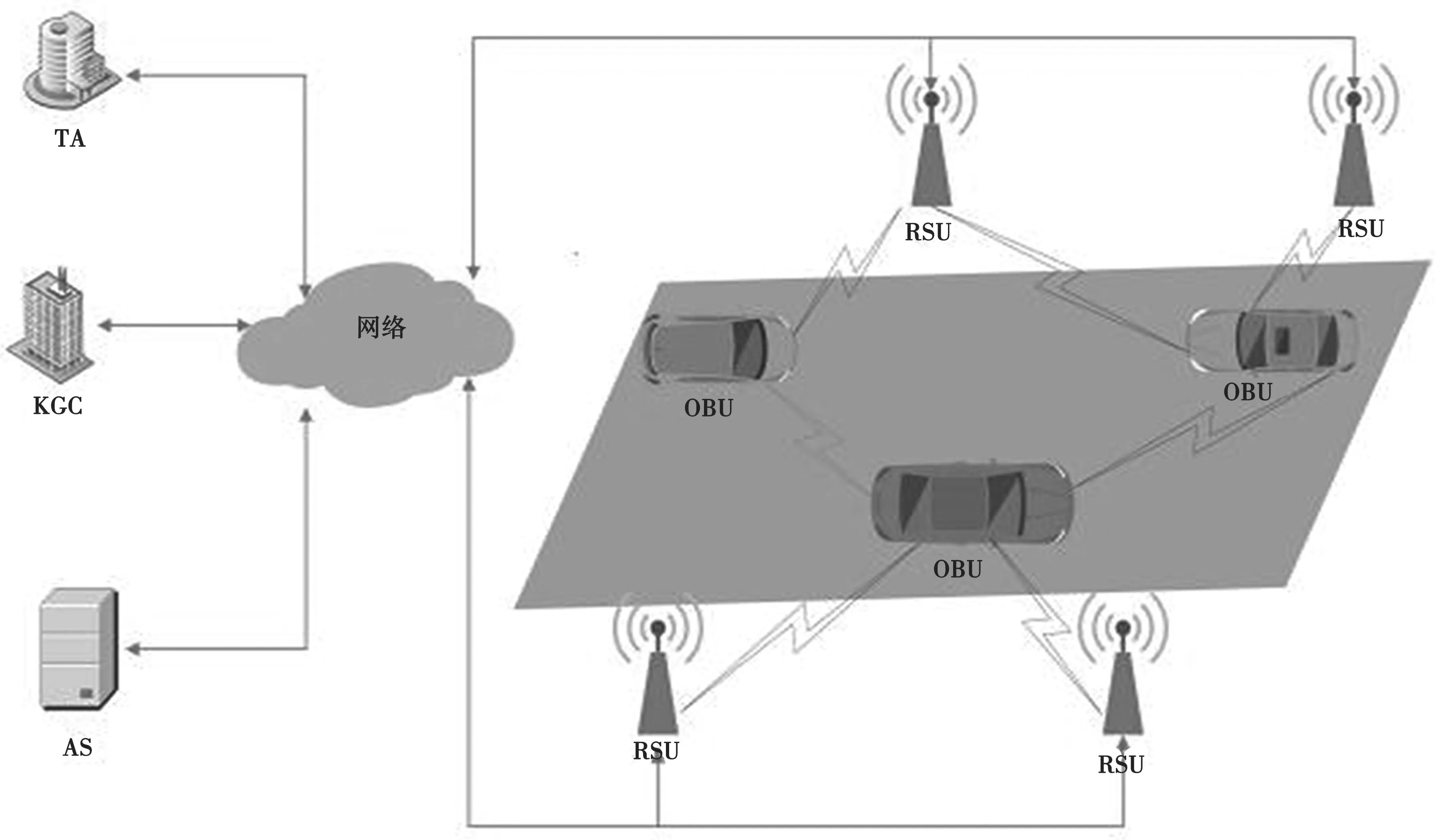
图1 VANET 系统模型

在实际部署VANET 时，安全和隐私是需要认真关注的两个问题。安全的车辆通信可以提供多种好处，如交通监控、避免交通事故、缓解交通拥堵、减少温室气体排放以及提供与交通相关的信息。因此，必须保护VANET 通信免受敌手和未经授权用户的攻击。此外，用户的隐私必须得到保护，因为用户的私人信息如旅行路线、身份、位置等暴露给未经授权的用户，可能会导致用户被跟踪和危害。由于VANET 中传输的消息性质特殊，通过数字签名实现的消息认证是VANET 确定和过滤未经授权用户的关键安全需求。由于大多数智能设备只拥有有限的存储空间和电力资源，传统的密码体制不适用于VANET，因此人们更关注设计轻量级和安全的密码协议。

在数字签名方案中，签名者用私钥对消息进行签名，验证者用相应的公钥对签名进行验证。签名者是唯一持有密钥的人，因此也是唯一能够产生签名的人，这是保证签名有效性的依据。作为签名者身份的重要见证，公钥的合法性保障至关重要。在传统的公钥密码体制中，用户的公钥和身份存储在某些可信机构颁发的证书中，而管理证书需要大量的存储空间和计算时间。基于身份的公钥密码体制[4]消除了复杂的证书管理问题。在该密码体制中，用户的电子邮件地址等身份信息直接用作公钥，而相应的私钥由密钥生成中心（Key Generation Center，KGC）根据系统主密钥和用户身份生成。此时，KGC 能够以系统中任何用户的名义解密和签署消息，给该体制带来了密钥托管问题。为了解决上述两个问题，AI-Riyami 和Patterson 引入了无证书公钥密码的概念。该密码体制中虽然有第三方KGC，但此时的KGC 只提供用户的一部分私钥，另一部分私钥由用户自己生成。用户的公钥通常是根据用户自己选择的秘密值计算的，因此该密码体制中不存在以上两个问题，更适用于VANET 环境。

Al-Riyami 和Paterson[5]提出了第一个无证书签名方案，并定义了其安全模型，之后无证书签名方案得到了广泛关注。文献[6]给出了无证书签名方案的通用结构。文献[7]指出Al-Riyami 和Paterson的CLS 方案无法抵抗两类敌手的攻击。之后，Yap等人[8]设计了一种新的CLS 方案，但Park 等人[9]证明了该方案在公钥替换攻击下是不安全的。Liu等人[10]提出了第一个标准模型下的CLS 方案，但该方案容易受到第Ⅱ类敌手的攻击。Hu[11]等人给出了CLS 方案的简化定义，之后有很多学者提出多种新的CLS 方案[12-15]。聚合签名[16]允许一种有效的算法将n个不同消息的n个签名从n个不同的用户聚合成一个签名，由此产生的聚合签名可以使验证者相信n个用户确实对n个消息进行了签名。这一特性对于资源受限设备的认证非常有吸引力。Zhang 等人[17]给出了无证书集合签名方案的概念和安全模型，并设计了一种安全有效的无证书聚合签名方案。同年，Zhang 等人[18]提出设计了两种无证书聚合签名方案，这该两个方案各有优缺点。之后，有很多安全高效的无证书聚合方案被提出[19-21]。

无证书聚合签名方案由于其自身的特点，比其他数字签名方案更适用VANET。CUI 等人[22]针对VANET 受带宽和存储约束的性质，提出了一种基于椭圆曲线无配对的无证书聚合签名方案，在计算和通信成本方面比之前的VANET 认证方案要低。但是，Ogundoyin[23]发现该方案在现有安全模型下是不安全的，且提出了一种新的基于椭圆曲线加密的无证书聚合签名方案，不仅满足VANET 的隐私性和安全要求，而且支持批量处理验证、自主性和有条件的隐私保护。Wang[24]等人为了实现VANET中车辆节点间信息传输的安全认证，设计了一种无证书聚合签名方案，并模拟了VANET 环境中的交通密度与消息验证时间延迟之间的关系。结果表明，该方案满足消息认证、匿名性、不可伪造性和可追溯性，更适合于动态的VANET。Kumar 等人[25]提出了一种基于无证书聚合签名的VANET 安全认证方案，保留了条件隐私，其中由车辆生成的消息被映射到一个不同的伪身份，并在随机预言模型中证明了该方案对自适应选择消息攻击的安全性。Thorncharoensri 等人[26]为了提供云存储中数据共享的完整性、真实性、权限和隐私性，提出了一个可指定验证者的无证书聚合签名方案，可以为VANET 提供有效的隐私保护。Li 等人[27]针对现有方案存在的缺点，如许多方案不安全，攻击者可以伪造签名，以及即使有些方案安全但计算开销较大的问题，提出了一种新的无配对无证书聚案。该方案可以实现对车辆的隐私保护，同时方案的聚合签名长度是恒定的，可大大减少通信和存储开销，且在计算开销和通信成本方面优于最近的相关方案。本文在文献[30]的基础上提出了一个安全高效的VANET 无证书聚合签名方案，如图2 所示。

1 预备知识

1.1 椭圆曲线离散对数问题

对于椭圆曲线离散对数问题，假设G是一个q阶椭圆曲线加法群，其中q是大素数，P∈G是生成元，给定椭圆曲线上任意一个点Q∈G，对于Q=aP和，从Q计算出a是困难的。

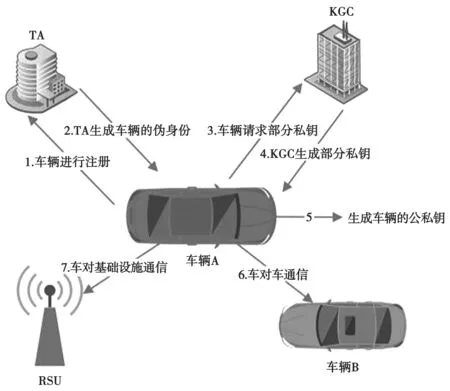
图2 本文方案所包含的步骤

1.2 CLAS 方案的安全模式

在CLAS 方案中有两种敌手Adv1和Adv2。Adv1模拟外部攻击者，没有系统主密钥和每个用户的部分私钥，但可以选择一个值来替换任意用户的公钥。Adv2充当恶意但被动的KGC，持有系统主密钥，但无法替换目标用户的公钥。

CLAS 方案的安全模型是由挑战者ξ和敌手Adv1、Adv2进行以下两个游戏来模拟。

游戏1 涉及到的实体是挑战者ξ和第一类敌手Adv1，他们的交互如下。

（1）系统初始化。由挑战者ξ执行，产生一个系统主密钥s和系统参数params，并将params发送给敌手Adv1，秘密保存主密钥s。

（2）询问阶段。敌手Adv1能够主动查询以下预言。

定义1：如果在游戏1 和游戏2 中没有敌手Adv1和Adv2能够在多项式时间内以不可忽略的优势获胜，则CLAS 方案在适应性选择消息攻击下是不可伪造的。

2 回顾Thumbur 等人的方案

Thumbur 等人的无证书聚合签名方案包含9 个算法。

2.1 系统初始化算法

对于给定的安全参数λ和大素数p，KGC 生成一个椭圆曲线E:y2+ax+bmodp和E上的q阶加法循环群G，其中且(4a3+b)modp≠0。KGC随机选择s∈Zp*作为系统主密钥，计算Ppub=sP作为相应的公钥。TA 随机选择b∈Zp*作为其主密钥，计算Tpub=bP作为相应的公钥。KGC 选择3 个安全的Hash 函数H1,H2,H3:{0,1}*→Zp*，并发布系统参数params={P,p,q,E,G,H1,H2,H3,Ppub,Tpub}。

2.2 伪身份生成算法

2.3 部分私钥生成算法

2.4 设置秘密值算法

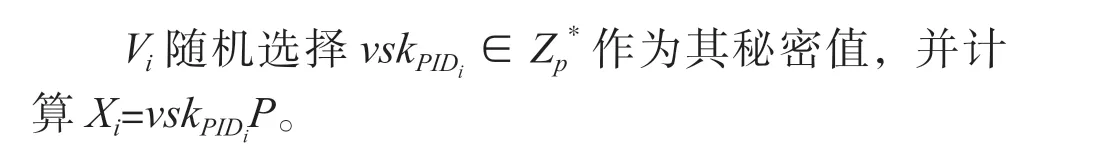
2.5 车辆密钥生成算法

2.6 签名生成算法

2.7 签名验证算法

2.8 聚合签名生成算法

2.9 聚合签名验证算法

3 Thumbur 等人CLAS 方案的安全隐患

从上面的签名伪造和验证过程中可以发现，伪造的签名是有效的，即第Ⅰ类敌手对Thumbur 等人方案的签名伪造攻击是可行的。

4 改进的方案

改进的CLAS 方案包括如下9 个步骤，其中符号和注释如表1 所示，本文方案如图3 所示。

表1 符号及其注释

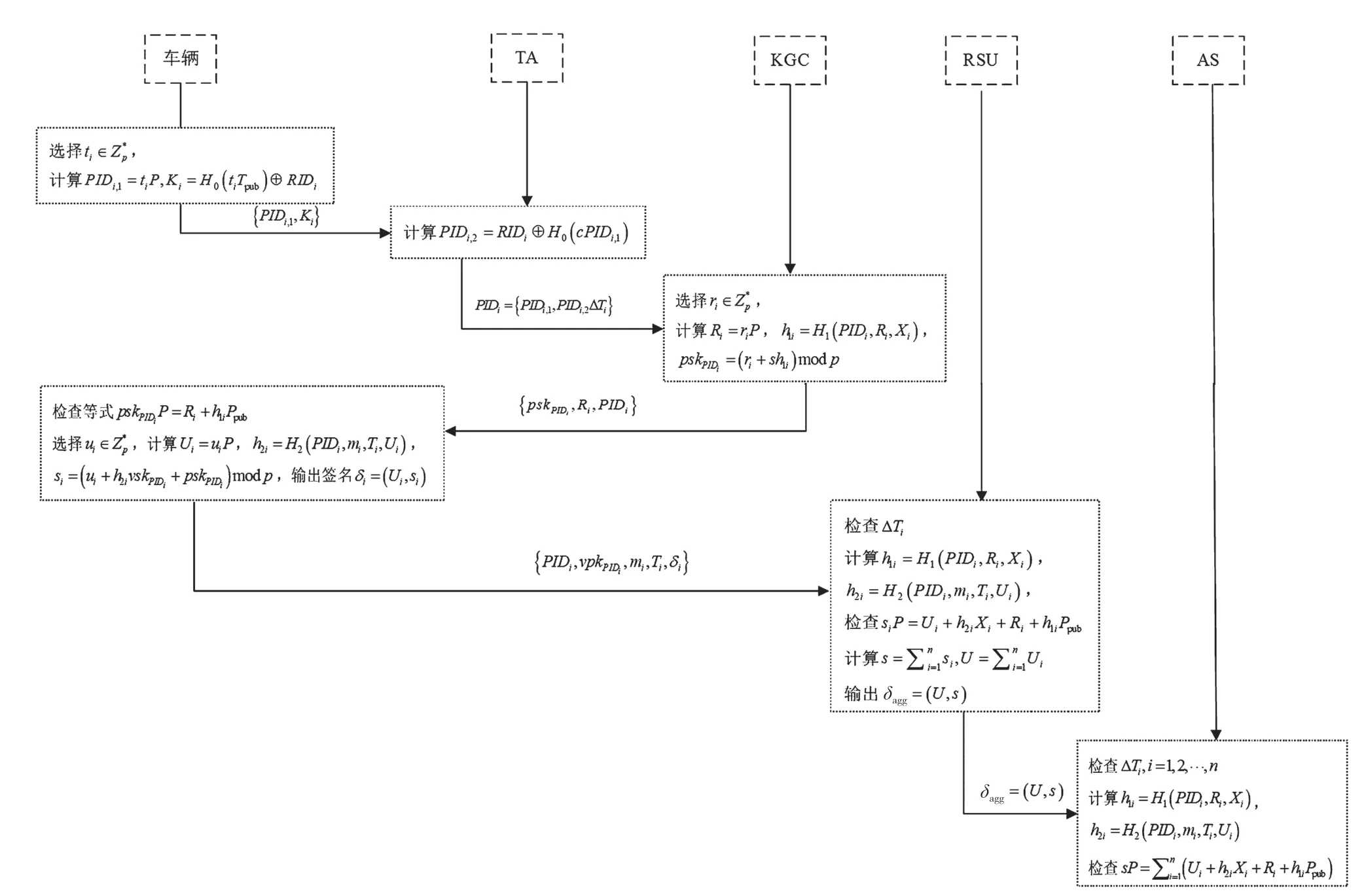
图3 本文方案

5 安全性分析

本节针对第Ⅰ类敌手和第Ⅱ类敌手，证明本文CLAS 方案的安全性。

定理1：假设不存在多项式时间算法解决椭圆曲线群中的椭圆曲线离散对数问题，那么本文CLAS 方案在第Ⅰ类敌手Adv1的自适应性选择消息和身份攻击下是存在性不可伪造的。

证明：假设ξ是椭圆曲线离散对数问题的挑战者，Adv1是一个第Ⅰ类多项式时间的敌手。Adv1可以通过在游戏1 中与ξ进行交互来伪造消息的有效聚合签名。假设ξ给出椭圆曲线离散对数问题中的一个实例(P,Q=sP)，ξ的目标是在与Adv1进行交互后找到s，ξ将PID*作为对消息m*的Adv1的目标身份。

（1）系统初始化阶段。ξ算法设置Ppub=Q=sP，执行执行系统初始化算法来生成params={q,G,P,Ppub,H0,H1,H2}，并将params发送给Adv1，秘密保存s。

（2）询问阶段。在这个阶段Adv1进行一系列询问，而ξ自适应地对其进行回答。

定理2：假设不存在多项式时间算法解决椭圆曲线群中的椭圆曲线离散对数问题，那么本文CLAS 方案在第Ⅱ类敌手Adv2的自适应性选择消息和身份攻击下是存在性不可伪造的。

该定理证明过程类似于定理1，不再进行证明。

6 效率分析

下面评估本文方案与其他5 个无配对VANET无证书聚合签名方案的效率。为了具备与1 024 位的RSA 相同级别的安全性，本文选择了一个非奇异椭圆曲线E:y2+ax+bmodp，其中a,b∈Zp*，G是E上的q阶加法循环群，且p和q是160 位的素数。不同操作的运行时间如表2 所示。

表2 不同操作的运行时间

6.1 计算成本

如图4 和表3 所示，文献[23]和文献[28-29]和本文的方案是安全的，文献[22]和文献[30]的方案存在安全缺陷。本文在签名阶段需要执行1 个点乘运算、1 个Hash 运算、1 个模乘运算以及2 个模的加法运算，在验证阶段需要执行3 个点乘运算、3 个点的加法运算以及2 个Hash 运算。该方案的总计算量为1.776 8 ms，比文献[22]和文献[30]的方案减少了19.8%，比文献[29]的方案减少了20%。就总计算成本而言，比Thumbur 等人的方案增加了0.07%。

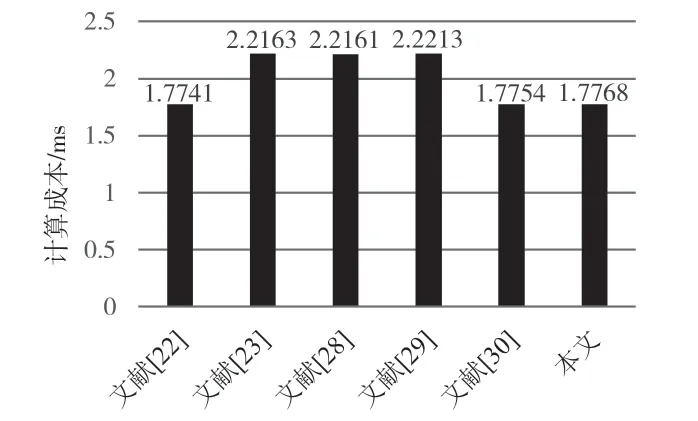
图4 计算成本比对

表3 计算成本比对

6.2 通信成本

本文考虑签名长度来评估本文方案与其他5 个方案的通信成本。如表4 所示，本文方案的聚合签名长度恒为480 位，通信成本与文献[23]一样，不会随着参与者的人数发生变化。

表4 通信成本比对

7 结语

由于其本身的优势，CLAS 在许多领域得到了广泛应用。为了设计一种安全有效的CLAS 方案，以满足VANET 的应用需求，本文首先对Thumbur等人的CLAS 方案进行了安全性分析，并证明了他们的CLAS 方案容易受到签名伪造攻击，后提出了一种新的无配对无证书聚合签名方案，并在随机预言模型中证明了其安全性，最后进行了效率分析和比较。安全性分析和效率分析表明，本文的新方案能够以更低的计算成本和通信成本获得更高的安全，且新方案的聚合签名长度恒定，大大降低了通信和存储开销，更适用于VANET 环境的实际部署。