基于KNN 的网络流量异常检测研究*

张 凡，高仲合，牛 琨

（曲阜师范大学，山东 曲阜 273165）

0 引言

随着互联网和移动设备的广泛使用，网络安全问题也越来越突出。要解决网络安全问题，需要准确地检测到恶意网络行为[1]。近年来异常检测在网络监控、捕获特征和流量分布等方面发挥越来越重要的作用。异常检测本质是一种数据的分类任务，对于分类任务来说，机器学习算法在这一领域已经取得了很明显的效果[2]。机器学习广泛用于网络异常检测中，例如，支持向量机（Support Vector Machine，SVM）、随机森 林（Random Forest，RF）、K-均值聚类（K-means）、K-最近邻算法（K-Nearest Neighbor，KNN）等。其中KNN 算法简单易于实现，并且支持特征的高维度计算，能在异常检测中展现较好的效果[3]。但传统KNN 算法在计算样本之间的距离时将属性的贡献看作是相同的，计算样本距离时权重是固定的，但在实际情况下，每个样本的属性贡献程度不同，这就会造成实际结果与预测结果严重偏离的问题。当数据分布不均匀时，样本数多的类别可能会有分类优势，这就会导致此类别中包含的属性参数频率相应的提高，从而当不同类别的近邻样本数相等时，很有可能因k的取值范围不同而错误分类。所以及时有效地检测到网络异常在网络安全领域具有重大意义[4]。

1 网络流量异常检测相关算法

1.1 KNN 算法

K-最近邻算法是著名的模式识别统计学方法，在机器学习分类算法中占有重要地位。KNN 算法中，首先计算给定测试对象与训练集中每个对象的距离，其次选定距离最近的k个训练对象作为测试对象的近邻，最后根据这k个近邻归属的主要类别来对测试对象分类。通常，KNN 在分类任务中使用“投票法”，即选择k个实例中出现次数最多的标记类别作为预测结果。在衡量样本距离时使用欧氏距离计算相似度。

设样本的类别由n个属性决定，即待测样本是n维向量，假设样本i的表示方法为表示样本i的第j个属性，因此可得到任意两个样本之间的欧氏距离：

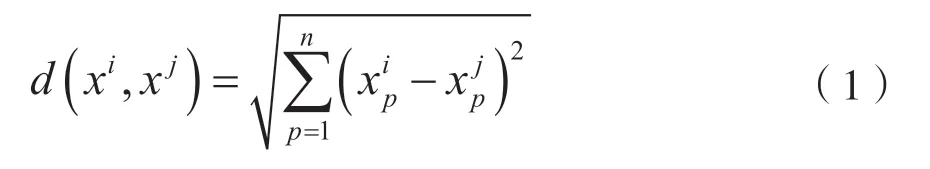
1.2 随机森林特征选择算法

随机森林是集成学习Bagging 类方法的一种，也是最早的集成学习算法之一。随机森林算法（Random Forest，RF）是利用多棵决策树对样本进行训练并集成预测的一种分类器[5]。它采用Boot-Strap 重抽样技术从原始样本中随机抽取数据构造多个样本，然后对每个重抽样本采用节点的随机分裂技术来构造多棵决策树，最后将多棵决策树组合，并通过投票得出最终预测结果。

使用随机森林选择特征的算法，利用特征重要性度量值作为特征排序的重要依据，特征重要性度量是基于袋外样本（Out-Of-Bag，OOB）的。通过分别在每个特征上添加噪声对比分类正确率的方式，来衡量特征的重要程度，当一个特征很重要时，添加噪声后，预测正确率会明显下降，若此特征是不重要特征，则添加噪声后对预测的准确率影响微小。在选择特征方面随机森林法已具有较好的效果，也有研究使用卷积自动编码器来进行特征降维，通过无监督学习剔除不重要特征，但无法得到属性的重要程度[6]。本文希望根据网络流量特征对于异常分类的贡献程度，赋予特征适当的权重。因此，计算特征的重要性度量和权重大小是一个关键的问题。为了消除数据不均衡带来的大偏差影响。

设原始数据集为D，特征个数为N，使用随机森林Bagging 方法对原始数据集进行Boot-Strap 取样，对原始数据集取样M次生成M个子数据集，在M个数据集上构造M棵决策树，则将数据集D划分为{D1,D2,…,DM}，根据划分后的数据集构造M棵决策树{T1,T2,…,TM}。在每一棵决策树上，通过给特征添加噪声对比分类正确率，得到一个特征的重要性度量。

设第j个属性的特征的重要性度量为θj，即对特征添加噪声前分类正确的个数RjF与添加噪声后分类正确的个数RjB之差，把每个子数据集再分别划分为五份，采用五折交叉验证计算特征的重要性度量。第j个特征的重要性度量IMij是由5 次产生的平均差值来决定。

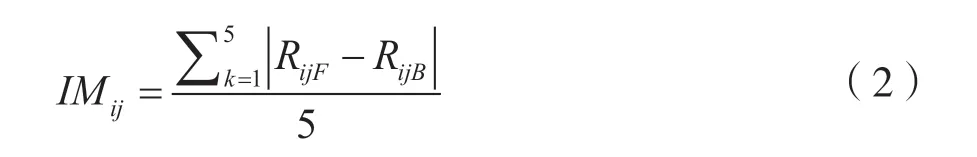
式中，RijF代表第i个子数据集第j个属性在添加噪声前分类正确的个数，RijB代表第i个子数据集第j个属性在添加噪声后分类正确的个数。

假设测试数据集有Q个样本，分成M个子数据集构造M棵决策树，每个决策树生成一个预测结果，M棵决策树的预测结果综合投票得到对于样本的集成结果。第i棵决策树的权重可由式（3）获得：

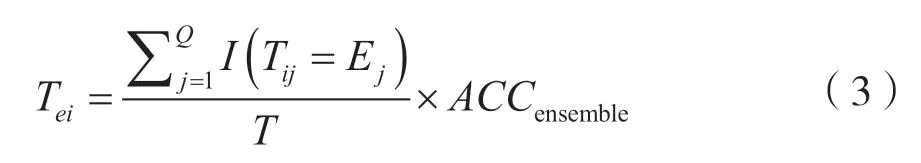
式中，Tij代表第i棵决策树对第j个样本的预测结果，Ej代表所有决策树对第i个样本的集成预测结果，ACCensemble代表集成预测的准确率。所以第j个属性的重要性度量值计算方法为：

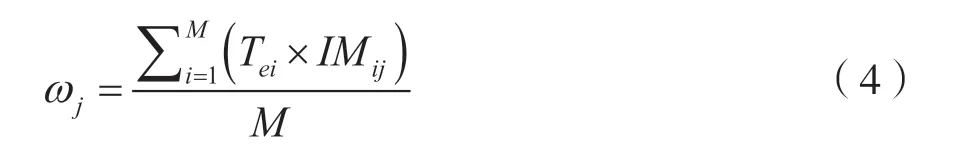
1.3 改进的KNN 算法思想

使用高斯函数对KNN 算法自适应地取K值，可以解决样本空间分布不均问题[7]。传统KNN 算法在分类时给予每个属性的权重是一样的。为区分属性重要性，本文用随机森林的算法判断属性重要程度并根据重要程度赋予其权重。在计算属性重要度时，它利用随机重采样技术Boot-Strap 和节点随机分裂技术构建多棵决策树，通过投票得到最终分类结果。算法采用属性与样本距离组合加权（Combined Weighted）的思想，提出了基于KNN的组合加权算法（CW-KNN），提高了异常检测率。在对样本距离加权时采用Gaussian 函数进行不同距离的样本权重优化，如果训练样本与测试样本的距离较远，该距离值权重就较小。也就是给更近的邻居分配更大的权重，而较远的邻居的权重相应地减少。

异常检测流程图如图1 所示。算法使用随机森林特征加权，那么计算距离公式为：

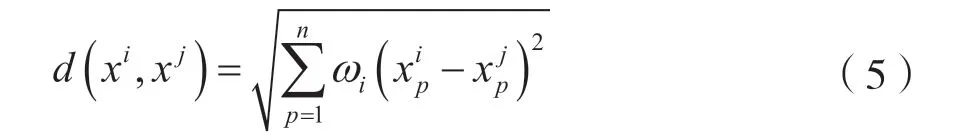
获得经过属性加权后的距离值，取距离最近的前k个元素，使用高斯函数对样本距离加权，在处理离散型数据时，将k个数据用权重区别对待，预测结果为与第n个数据的标签相同的概率：

在处理数值型数据时，对k个数据取加权平均，将每一项的距离乘对应的权重，然后将结果累加，求得总和后，再对其除以所有权重之和：

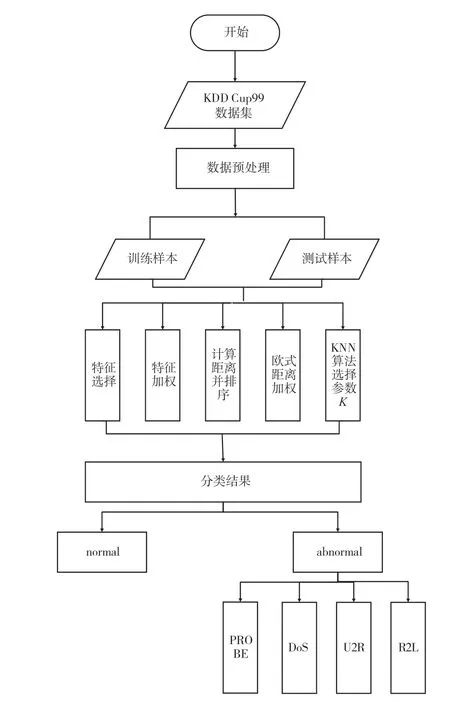
图1 基于KNN 的网络异常检测流程

高斯函数在距离为0 时，权重为1，随着距离增大，权重减小，但不会变为0，符合本算法对距离加权时的需求。高斯函数为：

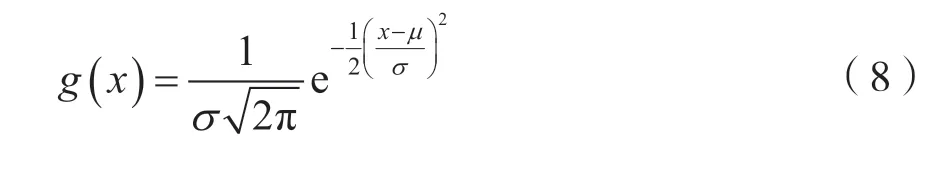
2 异常检测算法设计及数据预处理

异常流量检测是网络异常检测的重要研究内容，异常流量是在网络中与正常流量偏移较大的情形，正常流量会随着网络环境和用户的行为发生变化。因此，异常流量需要与运行在相同网络状态下的正常流量进行比对，才能判断出不正常的预期行为[8]。在流量检测的过程中，DoS 攻击的Bwd Packet Length Std 特征与其他类型的流量有较大的差异。正常流量与其他类型的攻击流量（除DoS）该特征值大部分为0，而DoS 攻击流量具有较大的数值。因此，通过学习流量的特征，就能正确识别正常流量与异常流量[9]。

2.1 算法设计

网络异常检测模型由数据收集及预处理模块，特征选择模块，流量分类模块组成。数据收集及预处理模块将KDD Cup99 数据集进行预处理，包括将字符型特征转化成数值型特征、数值标准化、数值归一化。特征选择模块使用随机森林算法判断属性重要程度并根据重要程度去除无关特征，按照属性重要程度进行加权。流量异常检测模块根据待测样本与训练样本加权距离，通过改进KNN 算法进行分类，以确定是否为攻击流量以及攻击类型。

2.2 数据集以及预处理

本实验使用KDD Cup99 数据集，共有311 029条数据，实验训练集与测试集比例为2:8。

KDD Cup99 数据集是从一个模拟的美国空军局域网上采集来的9 个星期的网络连接数据，分成具有标识的训练数据和未加标识的测试数据[10]。在训练数据集中包含了1 种正常的标识类型normal 和22种训练攻击类型，另外有14 种攻击仅出现在测试数据集中。KDD Cup99 训练数据集中每个连接记录包含了41 个固定的特征属性和1 个类标识，标识用来表示该条连接记录是正常的，或是某个具体的攻击类型。在41 个固定的特征属性中，9 个特征属性为离散（Symbolic）型，其他均为连续（Continuous）型。这41 个属性可以分为4类：TCP 连接基本特征、TCP 连接内容特征、基于时间的网络流量统计特征和基于主机的网络流量统计特征。数据集中异常数据类型分为DoS、PROBE、U2R 和R2L 共4 类。

3 算法实验与结果分析

3.1 实验设计

本节评估本文提出的算法的性能，所有的实验均在Windos10 操作系统中实现，选用KDD Cup99数据集，利用Python3 编译环境，结合Pycharm 编辑器实现对CW-KNN 异常检测算法的仿真。

3.2 实验评估指标

检测率（Detection Rate，DR）和误报率（False Alarm Rate，FAR）是决定异常检测算法检测精度的重要指标。检测率是指正确检测的异常数目占实际异常数目的百分比。误报率是指错误检测的异常数目占检测异常数目的百分比。基于混淆矩阵度量方程如下，其中TP是数据为异常且预测为异常的数量，TN是数据为正常且预测为正常的数量，FP是数据为正常但预测为异常的数量，FN是数据为异常但预测为正常的数量。本文利用以上指标对本文提出的异常检测方法进行验证。

检测率和误报率定义如下：

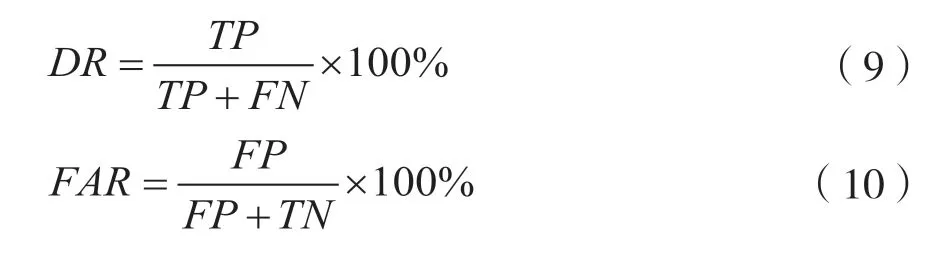
3.3 实验分析

本节重点评估结合KNN 算法，使用随机森林降维并为特征加权的方法进行异常检测所获得的结果。为了展示所建模型的有效性，使用KDD Cup99数据集进行了大量实验。实验效果与原始KNN 和基于距离加权的KNN（DIS-KNN）算法进行对比，验证CW-KNN 算法的实验有效性。从原始数据集中选取训练数据和测试数据的样本，为了表明提出的方法的有效性进行了广泛的实验，将K的参数取值范围确定为1、3、5、7、9、11，在一定程度上改变了最近邻居的数量，能有效地对比实验效果。结果如表1 所示。

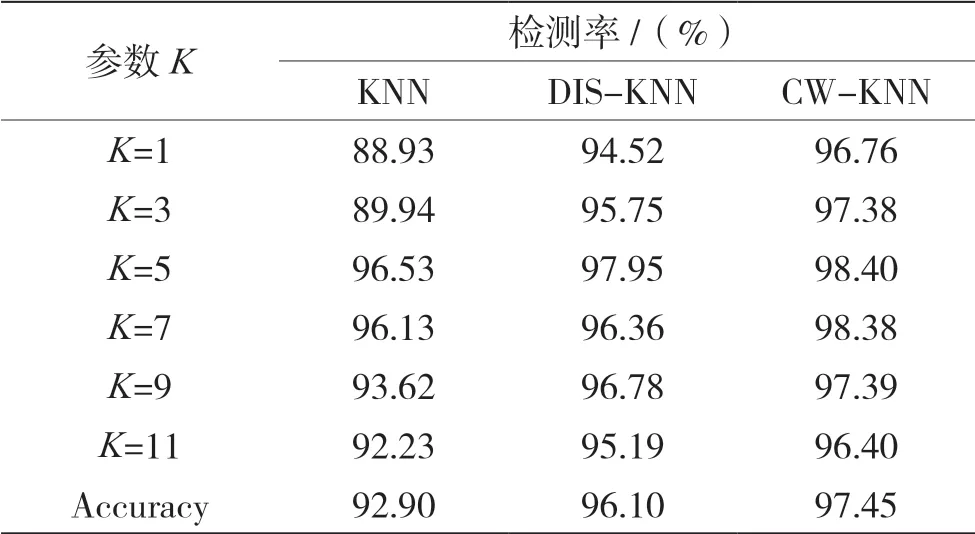
表1 不同K 值下检测算法的检测率对比

由表1 可以看出随着K的取值变化，3 种异常检测模型的检测准确率也随之波动，与KNN 与DISKNN（基于距离加权的KNN 算法）相比。CW-KNN算法的异常检测模型检测率较高，并能有效降低误报率和漏报率。可以看出，CW-KNN 取得了较好的检测率并相比较其他两种方法也更稳定。

由此可以分析：参数K取值在3～5 时，检测率有大幅度提升；当K＞9 时，各算法检测率逐渐降低；当参数K=5 时，CW-KNN 能取得最高检测率。整体来看，CW-KNN 能取得较高的检测率。

表2 和表3 验证了攻击类别的高发现率，对DoS 攻击的检测率可达到100%。与KNN 算法相比，在检测率方面CW-KNN 算法具有明显优势，由此可以验证CW-KNN 算法在网络数据流异常检测中的准确性。与原始KNN 算法和单一的距离加权的方法（DIS-KNN）相比，组合加权的KNN 方法具有较高的检测率。对于4 种攻击类型的检测率效果也比较理想，由于U2R 攻击类型在测试集中占比重较小，因此检测率较低，对DoS 攻击的检测率能达到100%，因此可以证明算法的有效性。

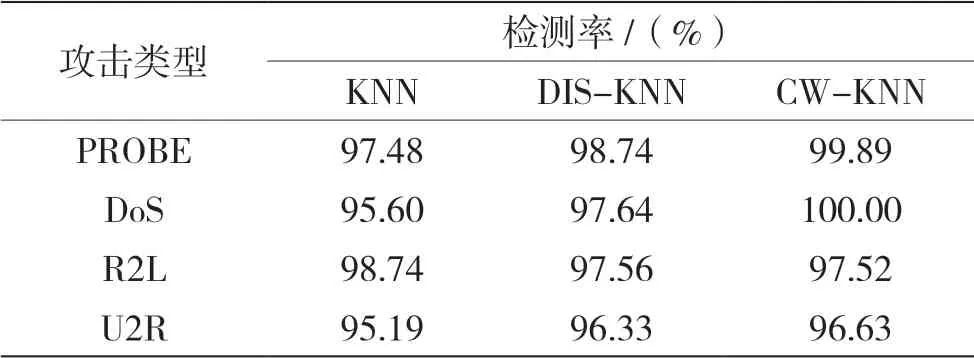
表2 CM-KNN 算法对于各攻击类型检测结果

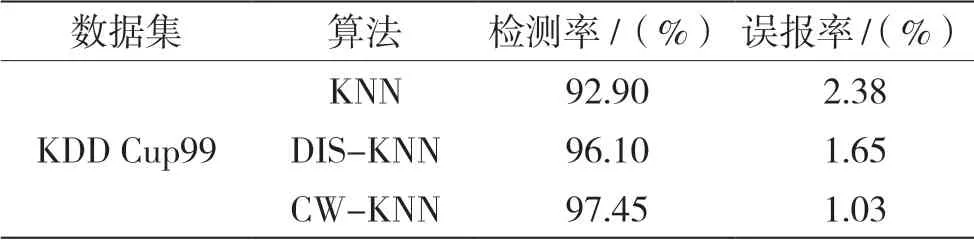
表3 各算法的检测率和误报率对比

4 结语

针对现在的网络异常检测方法检测精度不高，网络环境动态不稳定的问题，本文提出基于KNN的网络流量异常检测模型。使用基于KNN 的属性加权与距离加权相结合的方法进行流量异常检测，属性加权使用随机森林算法对属性重要性排序并对其加权，距离加权使用高斯距离加权。本文方法较好地优化了算法性能，提高了检测率，能有效检测各类攻击行为。由于KNN 算法对于高维数据计算量大，检测效率有待提高，下一步的研究重点是将无监督学习应用于异常检测，提高算法的健壮性和效率。