基于Abaqus 的某球铰翻边工艺仿真

刘建林 罗承俊 廖 勇 朱锦荣

（博戈橡胶塑料（株洲）有限公司，湖南 株洲412000）

1 概述

翻边工艺是球铰类产品生产过程中的一道重要成型工艺，将芯轴与橡胶硫化之后压装入球铰金属外套内，再经过模具的挤压，金属外套边缘发生卷曲变形之后得到最终产品。该工艺的一个重要目的在于保证球铰在受到额定大小的轴向力（简称为轴向窜出力）时，芯轴与外套不会发生脱离。翻边工艺的关键在于通过模具的挤压使球铰金属发生合理的卷曲变形，过大的卷曲变形会形成较大的残余应力，同时外套边缘易与橡胶发生剪切作用，影响球铰的使用寿命；卷曲变形程度过小通常难以满足球铰产品的轴向窜出力要求。翻边工艺的另一个关键在于变形量的确定。翻边后球铰的高度必须满足严格的尺寸要求，因此翻边前预留的金属外套高度及模具的形状与行程必须满足一定的要求。实际生产中，通常根据生产经验与现场试验结合的方式确定翻边工艺参数，存在产品设计周期长，生产成本高的问题[1-2]。随着计算机模拟技术的发展，通过对塑性变形过程进行模拟计算，可获得变形过程中成形材料及相关工模具热力学参数变化规律，从而为变形工艺的制定和工模具的设计提供依据[3-4]。本文拟针对某型球铰在翻边试制过程中存在高度尺寸超差的缺陷，采用有限元仿真分析技术对翻边工艺进行模拟仿真，得到翻边后球铰外套的应力应变分布与变形，并与试制结果对比验证了模型的准确性，同时根据分析结果调整工艺参数，分析数据表明工艺改进后的产品符合要求。

2 数值模拟

2.1 翻边工艺有限元计算理论

翻边工艺属于大变形问题，考虑与变形历史有关大变形问题采用增量方法：首先离散时间成某个时间序列，然后求解各个时间点上的数值解。这些数值解的计算方法，依照参考构形的区别可分为总体拉格朗日法（T.L.法）和更新拉格朗日法（U.L.法）。由T.L.法得到的有限元方程如式1 所示：

对上式展开求解，便可得到翻边工艺成型过程中的各项力学参数，具体的求解方法有隐式算法和显式中心差分法，本文选用隐式算法直接迭代求解，稳定性更好[7]。

2.2 几何模型与边界条件

图1 为翻边工艺试制的几何模型，主要几何尺寸如下：翻边前金属外套高度75mm，金属外套边缘外径、内径分别为56.8mm、52.8mm，模具的行程为11mm，支撑套高度h=42.5mm，要求翻边后产品的高度在68.5-68.9 之间。生产过程中，固定下模与支撑套，上模为主动模具，在外力持续作用下以1mm/s 的速度匀速向下运动，直到与支撑套接触。金属外套在上、下模具的挤压作用下发生卷曲变形，达到所需形状。

图1 翻边几何模型

2.3 计算模型及计算数据

翻边工艺属于轴对称问题，为缩减计算规模，将翻边工艺简化为如图2 所示的二维轴对称模型。为进一步提高计算效率，本文忽略上、下模具、芯轴以及支撑套在翻边过程中的微小变形，有限元模型中将这些部件设置为解析刚体[8-9]。运用Abaqus 中的CAX4R 单元模拟金属外套，CAX4H 模拟橡胶部分。本文分析的球铰外套为45 钢，弹性模量为2.1E5MPa，泊松比为0.3，屈服应力为375Mpa。翻边工艺属于大变形问题，因此为精确模拟金属外套在整个过程中的变形，需要输入该部件材料在塑性阶段的力学性能参数。橡胶胶料硬度为60sha，材料本构模型选用Mooney-Rivlin 模型，具体参数来自于TMT 材料数据库。

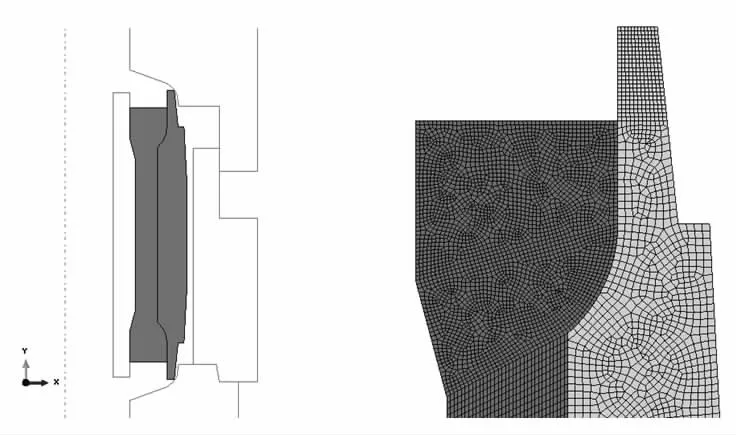
图2 翻边有限元模型

3 模拟结果与实验对比分析

翻边结束后金属外套的等效应力分布如图3 所示，变形集中于金属外套两端，最大应力为862.3MPa，位于金属外套边缘，如图3 中A 处所示。同时图3 中B 处金属外套边缘过于尖锐，在轴向动载荷工况下易与橡胶部分发生剪切作用而产生橡胶裂纹，降低球铰的使用寿命，建议增加倒角。利用Abaqus 软件测得翻边后球铰高度为69.81mm，产品试制结果实测为69.5mm，计算结果与实际误差不超过0.4%，一定程度上验证了模型的准确性。但翻边后球铰高度不满足68.5-68.9mm 范围，因此需要修改模具参数使其满足要求。

图3 翻边后金属外套的等效应力分布

由图1 直观分析可知，翻边后球铰高度尺寸与模具形状、行程有关。相对于修改模具形状，通过调整支撑套高度尺寸h 来改变模具的行程从而改变翻边后球铰高度尺寸更为经济，因此本文通过分析计算，在固定模具形状的前提下，研究球铰高度与支撑套高度h 之间的关系。通过一系列计算，将翻边后球铰高度与支撑套高度h 之间关系绘制成曲线，如图4 所示，近似为线性关系。

为使翻边后球铰高度尺寸满足68.5-68.9mm 范围要求，根据图4 选取h 为41.5mm；同时为减小图5 中B 处橡胶受到的金属外套边缘的剪切作用，对金属外套边缘倒圆角，根据工艺经验取R 为0.8mm。

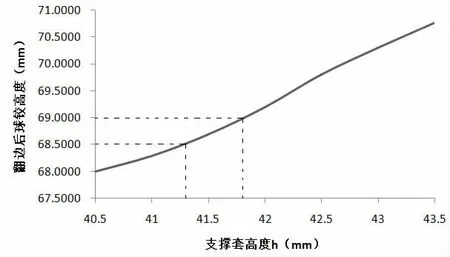
图4 翻边后球铰高度与支撑套高度关系

调整参数后的球铰翻边计算结果如图5 所示，球铰高度计算结果为68.7mm，满足尺寸要求，同时图5 中B 处所示外套边缘金属与橡胶接触更加平滑，橡胶受到的剪切作用大大减小，有利于提高产品的疲劳性能。

图5 调整参数后金属外套的等效应力分布

4 结论

4.1 通过仿真计算可以预测金属外套的变形与应力分布，并与实验吻合程度较高，分析结果可以为模具设计提供理论参考，从而达到减少产品试制次数，提高开发效率的目的。

4.2 经过仿真分析，得出支撑套高度与球铰高度之间关系，可以通过调整支撑套高度来获得满足尺寸要求的球铰。

4.3 适当增大金属外套边缘处圆角可以减少金属外套对于橡胶的剪切作用从而延长球铰产品的使用寿命。