基于小样本人工冻土冻胀率智能预测方法

姚兆明，左维亚，高亚飞

(1.安徽理工大学土木建筑学院，安徽 淮南 232001；2.陕西省一八五煤田地质有限公司，陕西 榆林 719000)

冻胀是寒区工程面临的主要工程病害，因此冻土冻胀变形的研究对工程建设和维护具有深远意义。国内外学者对此进行了深入研究。文献[2]考虑产生冻胀的各种因素，提出了一维条件下计算土体冻胀量的方法。文献[3]采用灰色关联理论分析了含水量、有机质、含盐量、土质和干密度对天山达板乔尔玛至那拉提公路延线冻土冻胀率的影响。文献[4]分析了含水量、初始干重、冻透率、地下水位、可塑性指数对冻胀率的影响，建立了预测冻胀率的统计模型。文献[5]对兰新高铁沿线四个断面进行了冻胀预测，测得其最大冻胀率，为了解高速铁路路基提供冻胀机理。文献[6]研制了1种测井测斜仪的简易斜臂仪，为研究冻融土壤的传热传质过程提供依据。

目前在岩土工程应用的智能方法有神经网络、支持向量机、遗传算法、鱼群算法、粒子群算法等。支持向量机(SupportVectorMachine，SVM)是由Vapnik等人在统计学习理论的基础上提出的，是在统计学习理论发展起来的基于结构风险最小化原则的机器学习理论，其具有较高的泛化能力。SVM可以较好逼近非线性复杂系统，能够有效解决过学习、维数灾难以及局部最小等问题。

目前支持向量机广泛应用于岩土工程领域尤其是冻土领域。如文献[9]基于多类支持向量机对土壤纹理进行分类。文献[10]利用机器学习模型SVM等分类器的预测，提出了1种新混合分类器集成，为岩土工程的其它分类问题提供了新方法。文献[11]采用主要成分分析法结合粒子群算法优化的支持向量机建立冻融土壤蒸发量的预报模型。本文采用支持向量机计算模型对冻胀率进行训练预测，对试验值和模型训练值、预测值进行对比、拟合、分析，以期为工程计算提供新的智能方法。

1 冻胀率试验

1.1 试验方案

文献[4]进行了不同土质参数的冻胀率试验。主要仪器设备包括试样盒、恒温箱、温度控制系统、温度监测系统、补水系统、变形监测系统和加压系统。土样为黏土、砂土、粉质黏土。三种土的粒径分级、极限含水量和总离子含量见文献。三种土样品直径均为11cm，红外光谱长度为130～150cm，在给定一定边界温度、初始干容重、含水量、地下水位条件下进行了69组土样冻胀率试验，得出试验结果。

1.2 冻胀率模型改进

文献[4]根据上述试验方案测得的冻胀率建立考虑了含水率、初始干重、地下水位、可塑性指数、冻透率对冻胀率的影响模型。该模型是基于最小二乘法拟合得到模型参数，参数缺少相应的物理意义，而且数学关系式很难控制多个变量，因此建立参数较少的数学模型很难解决此类问题，且试验方法求取冻胀率时会出现难度大、耗时、不经济的现象。因此可尝试一些机器学习方法，通过计算机来建立模型算法，本文将采用支持向量回归模型进行人工冻土冻胀率预测模型的构建。

2 冻胀率支持向量机回归模型

2.1 支持向量回归原理

支持向量机回归原理的基本思想就是寻找一个最优分类超平面，不仅将两类样本尽量正确分开，在保持较高分类精度的同时最大化分类间隔，而且使得样本的类内离散度尽可能的小。SVM将求解的问题最终归结为一个线性约束的凸二次规划问题，求出的解是全局最优的唯一解。

2.2 训练样本和测试样本

在支持向量机回归模型预测中，将已知数据看作一个大集合且分成两部分，其中一部分作为训练集，用来评价分类算法从而求出决策函数，剩余的部分作为测试集，测试所得决策函数的准确率，最后用得到的准确率作为评价算法优劣的标准。根据上述各个集合的目的及作用，将上述实验数据作为样本，由这些数据的学习训练建立映射关系。采取随机选取的方式从1～69组试验数据中选取10组试验数据作为测试样本，剩下的59组试验数据作为训练样本。试验数据来源于文献[4]，采用的支持向量机回归模型预测过程为： 输入参数为含水量

ω

、干重度

γ

、冻透率

V

、水头

H

、塑性指数

I

；输出参数为冻胀率

η

。 在训练及验证支持向量机回归模型时，对影响因素冻胀率因素采用公式(1)进行归一化处理，同时对冻胀率采用相同方法归一化处理。

(1)

2.3 核函数的确定

1)核函数的选取

核函数的选择不仅对支持向量机模型推广性能有很重要的影响，也对支持向量机模型精度有影响。现在常用的核函数包括线性核函数、高斯径向基核函数、多项式核函数、sigmoid核函数及自定义核函数等。

在以上几种常见的核函数中，线性核函数形式简单且误差比较容易估计，适用于低维且影响因素单一的小样本下的训练。多项式核函常用于一些经过正交归一化处理后的数据中。径向基核函数的收敛域相对较宽，无论是低维、小样本的训练样本还是高维、大样本的训练样本，径向基核函数都适用，是一种比较理想的分类、回归函数。根据各种核函数的形式、适用范围及本文的应用领域，选取多项式核函数(见公式(2))，和径向基核函数(见公式(3))对冻胀率进行模拟及预测。

多项式核函数

k

(

x

,

y

)=(

x

·

y

+1)

(2)

式中:

d

是整数，是自定义的参数。

径向基核函数

k

(

x

,

y

)=exp(-‖

x

-

y

‖/2

σ

)

(3)

式中：

x

为空间中任意一点；

y

为核函数中心；

σ

为函数的宽度参数。

2)两种核函数验证和对比

径向基核函数的惩罚系数

c

取21 000，多项式核函数的

c

取10。分别进行模型训练、预测。采用误差、均方误差以及平方相关系数对实验结果进行评价，其中均方误差计算如下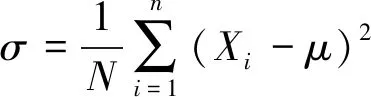

(4)

式中：

X

为变量，

μ

为总体均值，

N

为测试样本数。当支持向量回归模型的误差、均方误差越小，平方相关系数越接近1时，则模型的预测效果越好。径向基核函数和多项式核函数训练数据预测值和试验值如表1所示，预测数据预测值和试验值如表2所示。

表1 两种核函数训练数据预测值与试验值对比表 %

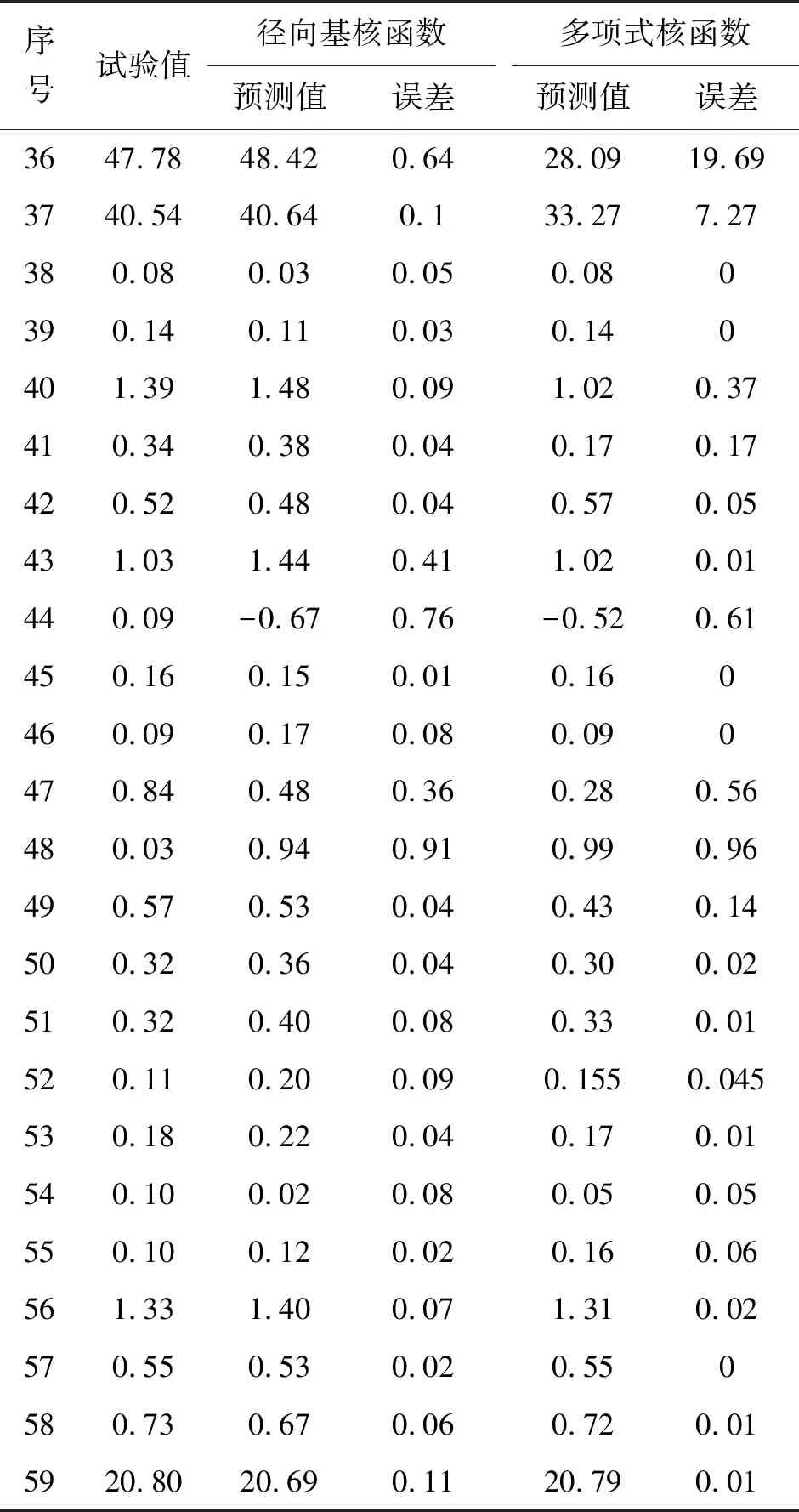
序号试验值径向基核函数预测值误差多项式核函数预测值误差3647.7848.420.6428.0919.693740.5440.640.133.277.27380.080.030.050.080390.140.110.030.140401.391.480.091.020.37410.340.380.040.170.17420.520.480.040.570.05431.031.440.411.020.01440.09-0.670.76-0.520.61450.160.150.010.160460.090.170.080.090470.840.480.360.280.56480.030.940.910.990.96490.570.530.040.430.14500.320.360.040.30 0.02510.320.40 0.080.330.01520.110.20 0.090.1550.045530.180.220.040.170.01540.100.020.080.050.05550.100.120.020.160.06561.331.40 0.071.310.02570.550.530.020.550580.730.670.060.720.015920.8020.690.1120.790.01

表2 两核函数预测数据预测值与试验值对比表 %

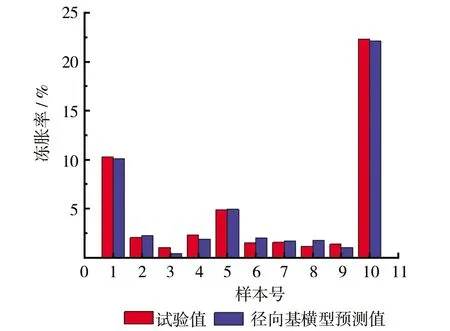
图1 径向基核函数模型预测值与试验值对比柱状图

图1为径向基核函数10组预测值的数值及试验值对比柱状图。通过对比柱状图中两数值可以看出两数值相差较小，拟合度也相对较高。

图2 多项式核函数模型预测值与试验值对比柱状图

图2为多项式核函数模型预测值与试验值对比柱状图，从中可以看出多项式核函数预测值与试验值相差较大，只有第1组和第8组数据较吻合。

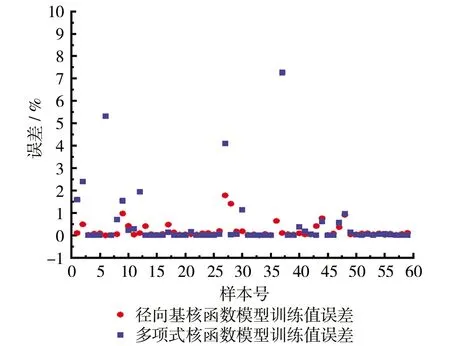
图3 两种核函数模型训练值与试验值对比散点图

图3为两种核函数模型训练值与试验值对比散点图，其中两种核函数预测的训练值与试验值走向均一致，两种核函数模型预测值均与试验值有差距，但和多项式核函数模型的差距更大。

图4 两种核函数模型预测值与试验值对比散点图

图4为两种核函数模型预测值与试验值对比散点图，图中表明径向基核函数预测值与试验值拟合度相对较高，而多项式核函数模型的预测值与试验值差别较大。

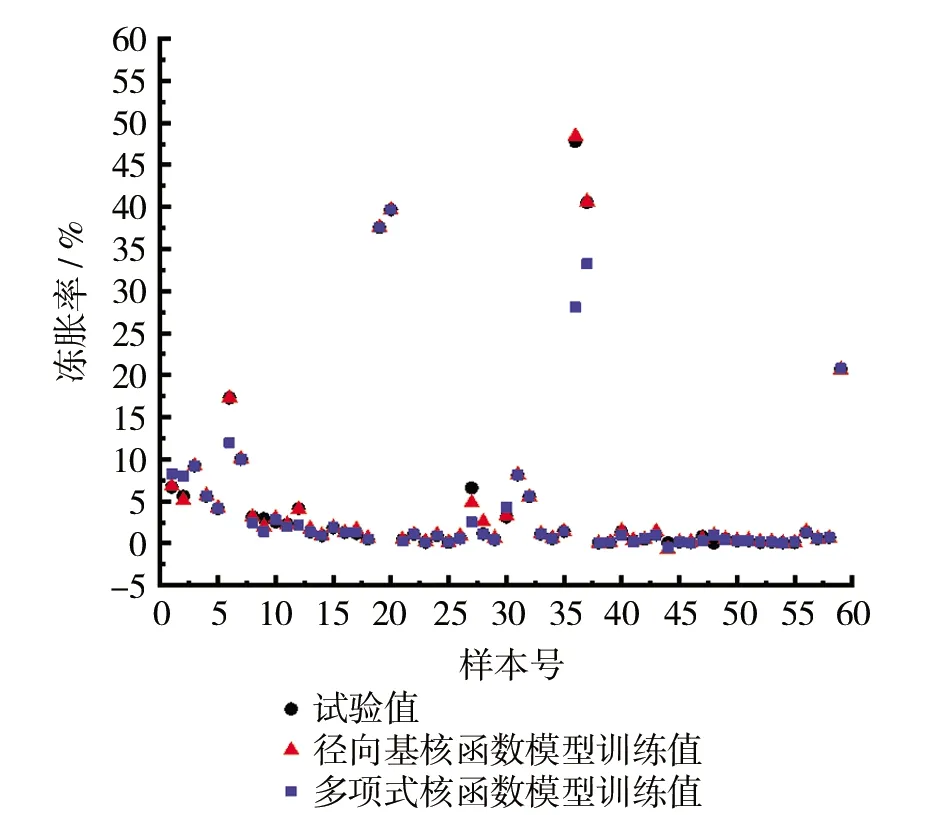
图5 两种核函数模型训练值误差对比散点图

图5为两种核函数模型训练值误差对比散点图，从中可以看出两核函数的误差相对较小，只有个别误差稍大。从图中可以看出，多项式核函数的训练误差与径向基核函数的训练误差相比，前者稍大一点且相差较小。

图6 两种核函数模型预测值误差对比散点图

图6为两种核函数模型预测值误差对比散点图，图中表明径向基核函数模型预测值误差相对较小，但多项式核函数模型预测误差值误差相对较大，且明显比径向基核函数误差大的多，尤其是第4个样本、第5个样本、第9个样本相的较多。

通过对比多项式核函数和径向基核函数的支持向量机模型训练、预测的误差对比表、点状图及柱状图，可以看出两核函数的平均误差较小。根据表1、表2可算得径向基核函数的预测的平均误差为0.31%，训练的平均误差为0.20%，均方误差为0.15，平方相关系数为0.998 6。多项式核函数的预测的平均误差为1.03%，训练的平均误差为0.84%，均方误差为7.55，平方相关系数为0.939 2。对比两核函数的训练平均误差、预测平均误差、平方相关性系数，可得采用径向基核函数的支持向量机模型的预测效果更好。

3 结论

研究发现径向基核函数支持向量机回归模型的预测效果更好。建立的冻胀率计算模型将支持向量机在人工冻土方面应用进行了拓展，模型提供了冻胀率计算一种新的智能方法。但支持向量机回归模型结果的准确性和可靠性取决于所选用训练样本的数量和质量。要做到对人工冻土冻胀率精准预测，需要进一步开展人工冻土冻胀率试验研究。