基于改进滑模变结构的加筋板振动控制研究
马天兵,丁威海,周 青,杜 菲
(安徽理工大学机械工程学院,安徽 淮南 232001)
随着工业领域对于材料各项性能要求的提高,高强度、强耐用性的加筋板结构的应用也愈发广泛。但是当加筋板结构受到外力扰动时,会产生振动,并带来一系列不利影响,因此对其振动的控制十分必要。加筋板控制系统中常采用反馈控制、线性二次高斯(LQR)、鲁棒控制等方法,其中,滑模变结构控制广受国内外研究学者的青睐。
滑模变结构控制算法属于非线性控制算法范畴,此控制策略与其他方法不同之处在于系统是动态变化的,控制过程中无需系统在线识别,并且不受系统参数的影响,这就使得滑模变结构控制具有一定的抗干扰能力,具备鲁棒性。文献[10]利用自适应滑模变结构控制方法,解决航天器姿态控制系统中的强非线性位姿控制问题,并且消除了外界不确定扰动力对于航天器飞行姿势形态的干扰。该方法很好地凸显了滑模变控制算法具有的较优的抗扰动效果。文献[11]对PWM整流器模型预测控制稳态波纹大、采样频率高、开关频率不固定等问题,结合了滑模控制,研究了一种新的种改进的模型预测控制方法。相对于传统的模型预测控制,改进后的方法能够显著地减小功率脉动,增强系统的动态性能和稳态特性,取得了不错的效果。文献[12]在研究磁悬浮轴承转子系统时,结合该系统的强非线性特征,提出一种Terminal滑模变结构控制算法,并设计了4输入4输出的控制策略,使得磁悬浮轴承转子系统有了更高效的控制。此方法与传统的PID控制器的控制结果相比,具有很好的抗干扰能力,并且在很短的响应时间内减弱抖振现象。文献[13]对于汽车制动过程中防抱死制动系统具有的非线性、时变性和不确定性的问题,设计了以最佳滑移率为目标的滑模变结构控制器,并且采用径向基神经网络实时调整滑模变结构控制器参数,削弱了滑模变结构控制中的抖振现象,并能使车辆具有良好的制动效果。尽管滑模变结构控制具有很好的抗扰动能力,但控制抖振现象在滑模变结构控制中一直存在,但抖振的产生与控制的抗扰动能力是相关的,需要权衡两者以达到较好的稳态。
针对滑模变结构控制中的抖振问题,文献[14]在滑模算法控制电机的基础上加入了模糊切换增益控制,不但没有影响滑模控制响应速度快的优点,并且相对于单纯的滑模控制电机,加入模糊切换增益算法,有效的减少了电机跟踪正弦曲线的抖动。文献[15]利用神经网络与滑模变结构相结合的复合控制方法来解决这一问题,并在伺服系统的时变性问题上得到了应用。但大部分学者通过研究如何改进滑模变结构中的趋近律,来减弱抖振现象。文献[16]在研究永磁同步电机的转矩波动问题时,设计一种新型滑模趋近律,对比电机在传统指数趋近律下的转矩抖动,该方法使抖动得到了很大的改善。并且该新型趋近律下的控制系统具有抖动小,自适应性强等优点。文献[17]提出一种将分数阶PI与变速趋近律相结合的改进型PI趋近律,基于该改进趋近律下的滑模控制算法减弱了系统输出的抖振问题,并且鲁棒性强。综上,研究学者们在看中滑模变结构控制具有抗干扰优势的同时,通过对趋近律进行改进来获取抖振小、鲁棒性强的控制系统成了振动研究的热门与趋势。
针对滑模控制系统抖振等问题,本文选择压电加筋板作为研究对象,对传统趋近律进行改进,并证明其收敛性,为验证改进趋近律控制效果,搭建加筋板仿真控制系统和实验平台,仿真与实验验证改进算法的控制有效性和优越性。
1 滑模变结构原理及收敛性证明
抖振问题是滑模变结构控制中一直存在的问题,也是历来人们研究的重点,其特点在于它可以削弱但不可消除,如果消除了抖振,也就消除了变结构控制对外界抗扰动的能力,从而失去鲁棒性。为了削弱控制的抖振问题,同时又要在有限时间内到达切换面,并且快速趋近滑动模态,那么,可以从趋近律方面入手,进而改善运动轨迹的动态品质。目前较为常见的有
(1)指数趋近律

(1)
式中:s
为超曲面,k
是趋近律,ks
为指数趋近项,sgn为符号函数,ε
为速度。其中,ks
为指数趋近项,当s
较大时,即运动点离切换面较远,系统能快速趋近切换面,并且指数趋近律还能使运动点在即将到达切换面时速度较小。同时为了保证有限时间内抵达切换面,满足切换面上存在滑动模态的条件,式中等速趋近项 的作用就是使运动点接近切换面时,速度是 而不是0,保证有限时间内趋近。(2)幂次趋近律

(2)
式中:α
为常数。另一方面,在执行过程中要坚持以人为本,讲究实事求是。管理者要对制度内容和要求了然于胸,对于组织成员要一视同仁,奖罚分明。其他组织成员要对管理制度清晰认识,遵守制度。对于违反管理制度的成员要惩处,树立制度的权威,促使组织成员从上到下自觉维护,保证制度对管理工作的高效作用。
同样为了较快进入滑动模态,幂次趋近律可以调整 值大小,使运动点离滑动模态较远时以较快的速度向它靠近,靠近滑动模态(s
较小)时,则保持较小的控制增益,可以降低抖振。结合考虑传统幂次、指数趋近律的优缺点对趋近律进行改进,改进趋近律如下
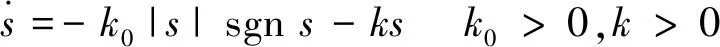
(3)
改进的趋近律可以看成在指数趋近律的基础上把速度项改成k
|s
|,使系统接近切换面即s越小时,趋近速度越小,减少抖振;也可以看成对幂次趋近律增加了一个指数项-ks
,使运动点离切换面较远时以一个较快的速度趋近切换面,保证快速趋近,这样就满足了快速趋近和较少抖振的需求。“滑模”区域上的点都是终止点,运动的点在该区域运动将会被“吸引”在该区域,该区域附近的点都将满足

(4)
为了说明改进趋近律的运动点也具有这一特性,需要对其进行验证。首先,根据实际被控对象压电加筋板模型

(5)
式中:x
代表结构振动位移,f
(x
,t
)是加筋板振动函数,b
为常数,u
(t
)为控制输出电压,d
(t
)为外界干扰。以及跟踪误差:e
(t
)=x
(t
)-x
(t
),其中,x
(t
)和x
(t
)分别是参考模型的位移以及加筋板的实际位移。对其进行滑模函数设计为
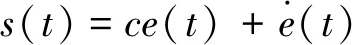
(6)
对式(6)进行求导,可以得到如下

(7)
由式(3)和式(7)可以得到等式

(8)
将上式化简,则可以得到

(9)
对于干扰d
(t
),由于是未知,我们可以利用干扰界来进行设计。将d
(t
)取为d
,其中d
为跟干扰界相关的正实数。则
(10)
将式(12)代入式(8)中并化简得到

(11)
假使对于d
(t
)干扰的上下界为d
和d
,则d
≤d
(t
)≤d
(12)
那么对于实数d
的选取,如下

d
进行设计如下
(13)

2 改进滑模变结构仿真控制
2.1 加筋板模态参数识别
搭建加筋板实物作为后续控制研究对象,具体为尺寸为400mm×600mm×1.2mm的壁板。主要控制的是加筋板的第一阶模态振动。实验中的扫频信号采用60~300Hz的正弦信号对加筋板进行扫频激励,利用实验模态分析方法获取的一阶模态振动频率为f
=213.4Hz,运用半功率带宽阻尼分析法得第一阶阻尼比为ξ
=-0.012 9,通过实验测得δM
=0.1m,其中δ
为力因子,为一阶模态下的模态质量。综合上述结果可得一阶模态的空间状态方程为
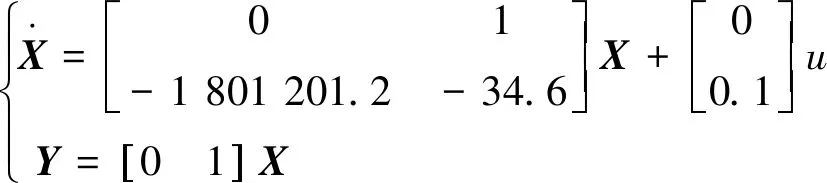
(14)
2.2 仿真结果及分析
在MATLAB里编写指数趋近律、幂次趋近律和改进趋近律3种滑模控制器程序,为保证对比有效性,其中共同参数选择相同值,令k
=100、c
=50、k
=1 000、b
=0.07; 而不同算法内的独属参数则选择效果最佳参数,多次实验下发现取值ε
=2、α
=1.5时效果最佳。分别对不同趋近律控制器下的系统进行仿真控制,激励信号设置相同,系统中积分初始值均取0,仿真时间为0.5s,经过仿真控制系统运行,3种不同控制算法下控制前及控制后的振动位移对比结果如图1~图3所示。

图1 基于指数趋近律的滑模控制仿真结果

图2 基于幂次趋近律的滑模控制仿真结果
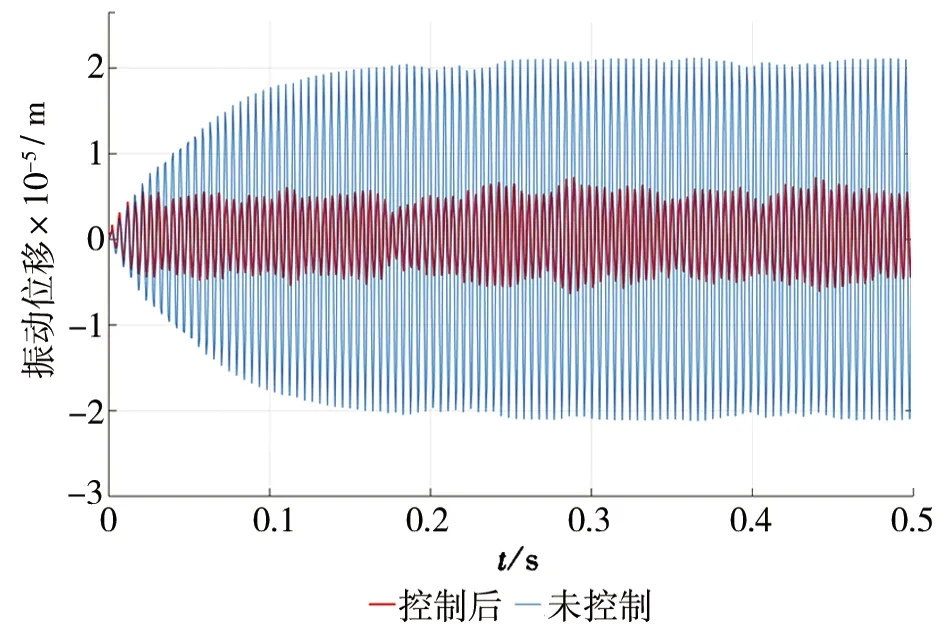
图3 基于改进趋近律的滑模控制仿真结果

图4 不同方法控制效果局部放大图
根据图1~图3仿真控制结果可知,三种控制均达到了振动控制的效果,但控制效果的好坏存在差异。3种控制方法在未控制前的振动位移均稳定在2.11×10m左右,在分别基于指数趋近律、幂次趋近律以及改进趋近律的3种滑模控制器下,振动位移分别被控制至6.70×10m、7.52×10m、4.95×10m,可以看出,基于改进趋近律控制下的控制结果振动位移最低,振动控制效果最佳。根据振动控制波形结果可知,改进趋近律的滑模控制可使被控振动信号更快进入稳定状态,根据图4可知,相对于指数趋近律和幂次趋近律,采用改进趋近律控制后的抖振现象不显著,说明该方法对抖振实现了较好的抑制作用。仿真效果综合来看,基于改进趋近律的滑模控制器能够很好地实现振动控制,并且具有一定的优越性。
3 改进滑模变结构振动控制实验
3.1 实验平台搭建
本压电加筋板振动主动控制实验是在CompactRIO(CRIO)平台下的振动控制实验,所用压电传感片和压电作动片的尺寸规格是50mm×50mm×0.2mm,粘贴于加筋板一阶模态振动最大处前后对称位置。由信号发生器输出正弦激励信号,激励信号的频率设置为加筋板一阶模态频率213Hz,经过功率放大器放大后,通过激振器作用于加筋板上,CRIO的信号采集模块采集压电传感片振动响应信号,经过CRIO实时分析运算后由输出卡输出控制制加筋板振动,实验平台如图5所示。

图5 振动控制实验平台
3.2 实验结果与分析
在信号发生器中设置正弦激励信号,频率为213Hz,通道采样率设置为10k,根据模态分析中的内容,加筋板参数取上文求取的模态参数。控制器参数按照仿真中选取的参数设定。实验时首先运行控制程序,待程序运行起来并且前面板中出现信号波形图,然后打开信号发生器,设定好激励信号后选择输出,驱动激振器进行激励,然后逐步缓慢调节功率放大器,调节输出控制信号的放大倍数直至运行稳定,并确保每种趋近律下的未控制前的电压幅值一致,经多次实验得到不同趋近律下的振动控制结果如图5~图7所示。为更好的说明控制效果,频谱选择包含213Hz振动频率的100~500Hz频段结果进行显示,由于频率分辨率的影响,该频段主要振动频率较为显著。
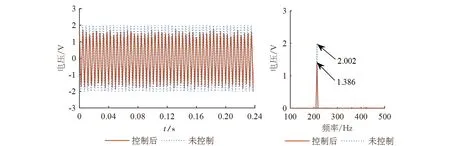
图6 基于指数趋近律的振动控制效果

图7 基于幂次趋近律的振动控制效果
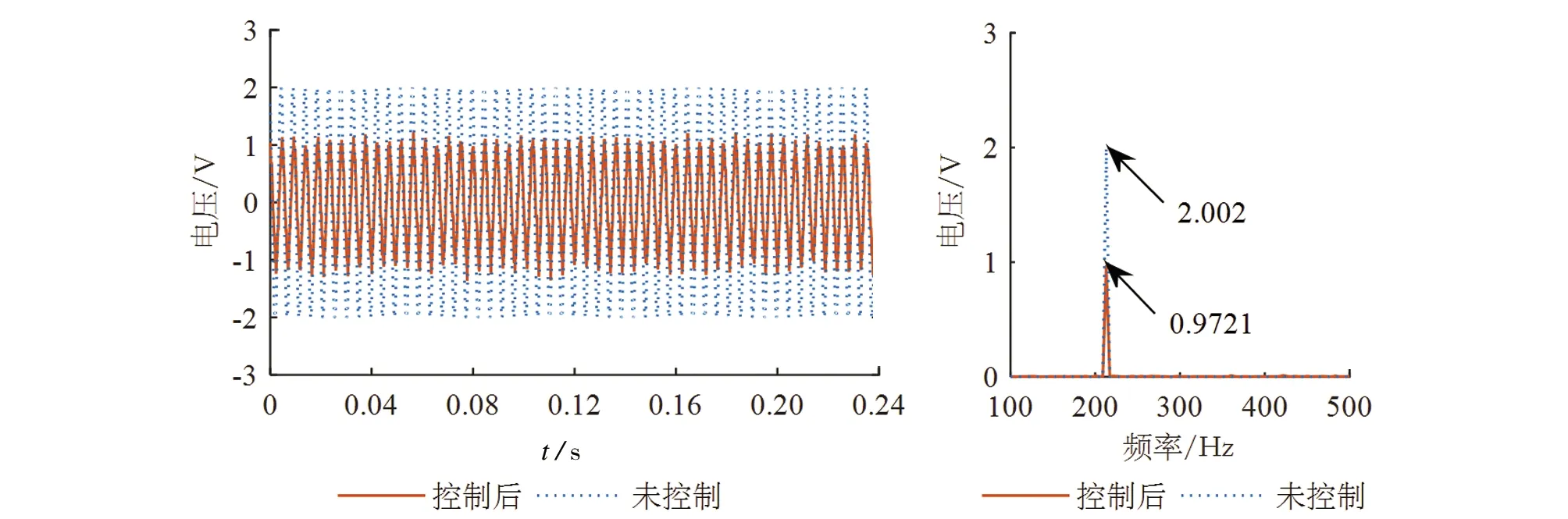
图8 基于改进趋近律的振动控制效果
根据图6~图8实验的时频域结果可知,基于改进趋近律的滑模变振动控制算法实现了振动控制,由未控制的2.002V下降至了0.972 1V,降低了51.4%,相较于指数趋近律30.7%以及幂次趋近律的36.4%的控制效果,明显较优。相对于指数趋近律以及幂次趋近律,基于改进趋近律抖振的高频振荡也得到了一定程度的削弱。
4 总结
本文综合考虑传统幂次、指数趋近律的优缺点,并在传统趋近律的基础上作了改进,得到新的改进趋近律,推导出基于改进趋近律的滑模控制器函数,并验证了其稳定性。在Simulink中设计振动控制仿真实验系统,仿真结果表明,相对传统指数趋近律和幂次趋近律滑模控制,改进趋近律的控制效果较佳,振动控制进入稳态较快,振动抑制效果也有所改进。此外,设计并搭建压电加筋板振动实验平台进行振动控制,实验结果同样表明,基于改进趋近律的滑模控制器控制效果可达到51.4%,能够较好地实现振动控制,能在一定程度上削弱抖振,并且相较于传统趋近律控制也具有明显的优越性。

