渭北旱塬黄土边坡稳定性分析及治理措施研究
——以三原县清河国家湿地公园为例
巨 龙,王瑞科,马 骥
(1.中国电建集团西北勘测设计研究院有限公司,西安 710065;2.河海大学,南京 210024)
0 引 言
黄土作为第四纪的沉积物,具有较强的结构性。土层中裂隙较发育,使黄土边坡的整体强度差。黄土天然含水量普遍较低,颗粒间的胶结物质耐水性差,土体含水量增大会弱化加固粘聚力的作用,使黄土的强度降低,导致许多工程破坏。
针对黄土边坡的特殊性,众多学者对黄土边坡的破坏机理及治理措施展开了大量的研究,所采用的研究方法不尽相同。杨海红等[1]在层次分析法的基础上建立AHP模型,用来对治理方案进行评价和优化。刘宝生等[2]采用现场调查、室内实验、理论分析和案例对比的方法对黄土边坡滑坡的成因机制进行分析,并提出有效的处理措施。随着数值模拟方法的不断发展,其在黄土边坡加固研究中也开始应用[4-6],众多研究成果证明数值模拟方法在黄土边坡研究中的可行性、有效性。
本文以陕西省渭北旱塬三原县清河湿地公园黄土边坡为研究对象,利用数值模拟方法对黄土边坡开挖及降雨过程的边坡稳定性影响进行计算分析,分析边坡的破坏过程和变形机理,提出加固措施,并对加固后的边坡稳定性进行分析,验证其加固效果,为黄土边坡的工程治理提供借鉴。
1 研究区域概况
研究区域位于泾河北岸渭河支流清河中游,河谷两侧发育河漫滩,一级阶地不发育,零星可见。两侧边坡高20~30 m,自然坡角上部近直立,下部35°~55°。三原县多年平均降水量536.6 mm,最大降水量829.7 mm,最小365.3 mm。降水量在时空上分配不均,主要集中在5—8月,占年全年降雨量的52%左右。根据GB18306-2015《中国地震动参数区划图》划定:工程区地震动峰值加速度0.15g,地震动反应谱特征周期为0.35 s,其相应地震基本烈度为Ⅶ度。
2 强度折减法
相比传统的极限平衡法,强度折减方法能够全面满足应变相容条件、静力平衡准则以及非线性本构关系,适用于材料不均匀且形状复杂的边坡,并且不需预先假定滑动面。
折减后的抗剪强度参数可分别表达为:
(1)
(2)
式中:C、φ分别为土体抗剪强度参数;Cm为土体粘结力;φm为土体内摩擦角;Fr为强度折减系数。
利用有限元强度折减法计算边坡稳定性时边坡失稳的判别依据常用的包括3种:以数值计算收敛与否作为评价标准;以是否形成连续的贯通区作为评价标准;以特征部位点的位移拐点作为评价标准。前两种方法影响因素较多,第3种方法的物理意义较为明确,便于理解。因此本次在使用有限元强度折减法对黄土边坡进行稳定性判定时,以特征部位点的位移拐点作为评价标准。
3 边坡稳定性计算分析
3.1 计算模型建立
在三原县清河湿地公园治理范围内,选取1个典型断面进行分析,在Abaqus中建立黄土边坡的二维模型。模型如图1(a)所示:总高度50 m,总宽度107 m,边坡高度24.7 m,坡顶宽度50 m,河谷宽度30 m。设计开挖分为两级边坡,上级边坡高12.3 m,下级边坡12.4 m,平台宽度2 m,如图1(b)所示。土体本构模型选用Mohr-Coulomb模型,剖分单元使用CPE3三节点三角形平面应变单元。
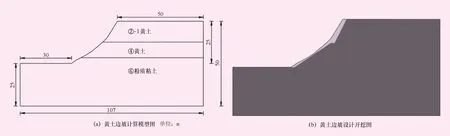
图1 黄土边坡计算模型图
3.2 计算参数及边界条件
模型边界条件:左右边界控制横向位移(U1=0),底部边界控制横向和纵向位移(U1=U2=0)。


表1 岩土物理力学参数表
3.3 渗流计算模型
土-水特征曲线是描述土体基质吸力和土体含水量之间的关系曲线,也可以描述土体的强度和渗透之间的一些特性。针对不同土体有多种土-水特征曲线的拟合模型,本次采用VG模型。
(1) Van Genuchten(VG)模型
该模型于1980年被Van Genuchten 提出,针对非饱和土体而言,表达式为:
(3)
式中:a、n、m分别为拟合参数;ψ为基质吸力,kPa。
本次计算得VG模型参数参考了《降雨入渗条件下非饱和黄土高填方边坡稳定性研究》一文中推算的黄土VG模型参数[3],具体参数如表2所示:

表2 VG模型拟合参数表
3.4 安全级别
滑坡治理范围处于三原县清河湿地公园内,坡脚范围有景观亲水平台,坡顶有居民房屋。边坡垮塌后可能造成人员伤亡或财产损失。根据GB50330-2013《建筑边坡工程技术规范》确定边坡工程安全等级为3级,边坡设计安全系数详见表3。

表3 边坡设计安全系数表
3.5 计算方案
本文设置了4种计算工况:天然工况、开挖不支护工况、正常运行工况、地震工况。各工况具体情况如下:
(1) 天然工况
按照现状地形,根据地勘资料及试验数据进行模拟计算。
(2) 开挖工况
拟通过两步对边坡进行开挖,第1级边坡开挖高度约12.3 m,坡比为1∶0.5;第2级边坡开挖高度约12.4 m,坡比为1∶1.5,上下级边坡之间保留2 m宽的平台。
(3) 正常运行工况
对边坡采用锚杆+格梁措施支护后,评价边坡稳定性。
(4) 地震工况
边坡支护后,按照工程区Ⅶ度地震烈度进行模拟计算,评价边坡稳定性。
(5) 降雨工况
对天然及开挖边坡模拟施加降雨,本次降雨模拟中采用的降雨强度32 mm/d(大雨)进行计算。在本次数值模拟过程中,边坡的坡比分别为1∶1.5和1∶0.5两种,通过转换可得到各个坡比下边坡的单位流量边界条件。
3.6 计算结果分析
3.6.1天然工况
(1) 天然工况模型
利用强度折减法对天然工况边坡进行计算分析,得到如下结果:
由图2可知,边坡滑动面较陡,符合黄土高陡边坡破坏时滑动面陡峭的特性以及黄土垂直节理发育的特征。如图3所示,该边坡的安全系数为1.15,边坡处于稳定状态,但不满足安全标准。

图2 天然工况水平位移云图
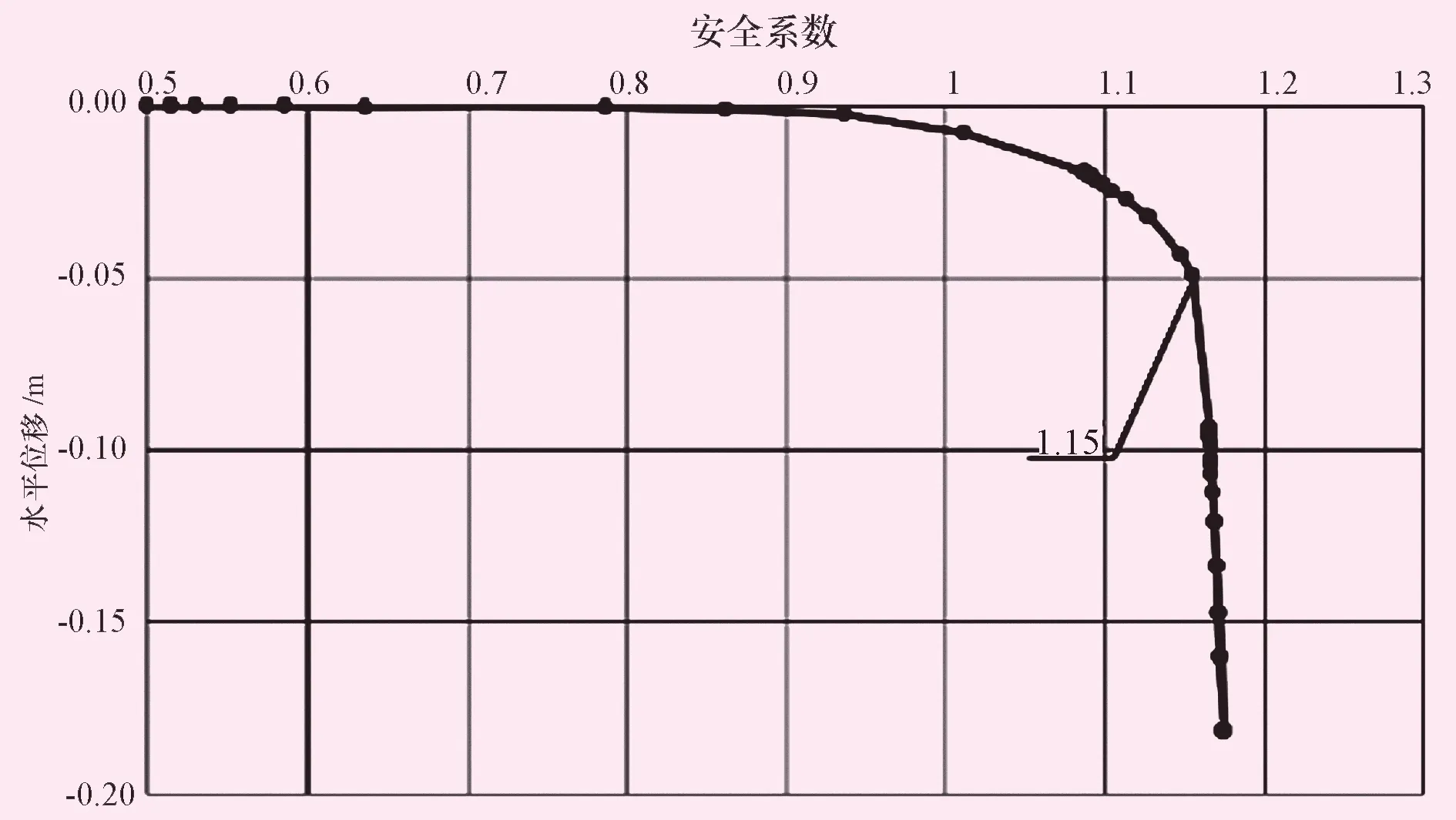
图3 天然工况水平位移随安全系数变化图
(2) 初始应力分析
利用强度折减法在Abaqus中对该模型进行分析,得到的边坡初始状态的应力分布云图。从边坡的初始应力云图中可以发现,边坡的坡脚和边坡中部应力值较大,分别选取边坡坡面上的部分节点来分析边坡应力分布,具体如图4、表4所示。
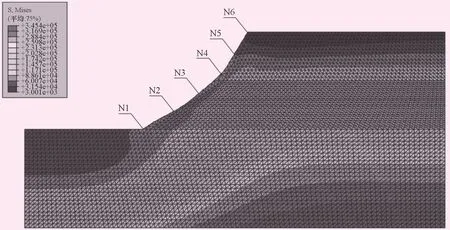
图4 黄土边坡初始应力云图
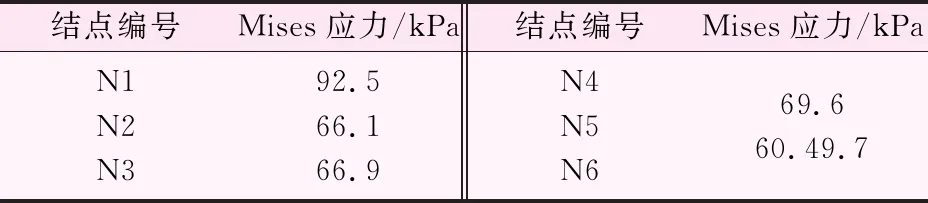
表4 边坡节点应力值表
3.6.2开挖不支护工况
(1) 开挖应力分析
对边坡两步开挖进行有限元分析,得到了两步开挖之后的黄土边坡应力云图,如图5、6所示。
第1步开挖后,下级边坡坡脚应力值由92.5 kPa变为86.5 kPa,应力值相比开挖前下降。主要是由于上级边坡削坡减荷作用影响,使得下级边坡坡脚处应力值降低。但是由于上级边坡坡度较陡,边坡坡率为1∶0.5,上级边坡坡脚应力会比较集中,开挖后上级边坡坡脚应力达到89.7 kPa,该处边坡应力值与开挖前N4节点应力值69.6 kPa相比有明显增大。平台左端位置应力值下降明显,开挖前应力值为72.4 kPa,开挖之后该处应力值为11 kPa。这主要是因为开挖之后该处以上的土体被直接清除导致。

图5 第1步开挖应力分布图

图6 第2步开挖应力分布图
第2步开挖后,应力变化主要在平台处,平台左端应力值为30.7 kPa,下级边坡坡脚应力值为90.7 kPa,应力均有所增加,这主要有两方面的原因:① 下级边坡开挖方量很少,主要是以缓坡为主,而且开挖前后边坡的坡率变化小,所以削坡带来的减荷作用较小,这点在边坡坡脚应力的变化值上可以较为明显得表现出来,两次开挖后边坡坡脚应力由92.5 kPa变为90.7 kPa,变化幅度很小;② 由于第2步开挖之后平台宽度减小,上级边坡对下级半坡的应力影响明显增大,详见表5边坡开挖应力分布情况表。
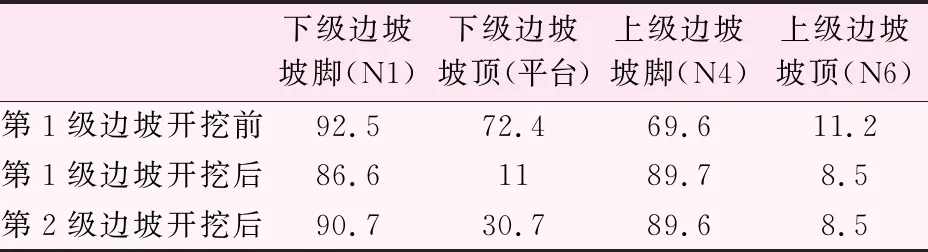
表5 边坡开挖应力分布情况表 /kPa
综合上述分析可以发现,两次开挖对边坡应力的分布影响相对较小。第1步开挖后,上级边坡的坡度较陡,坡脚应力较大,对边坡稳定性的改善非常有限,需通过其他支护方式对上部边坡进行进一步治理。第2步开挖之后,由于开挖量较小,平台宽度减少,上部边坡对下级边坡的应力影响增大,导致下级边坡坡脚的应力增大。

图7 边坡开挖后水平位移云图
(2) 开挖变形分析
通过对边坡分级开挖过程进行模拟计算,得到如下计算结果:
由图7可知,第1级及第2级边坡开挖后,第1级边坡坡脚水平位移向坡外分别为8.7 mm、9.1 mm。第1级开挖对边坡扰动更大。在开挖过程中应重点考虑上部边坡的稳定性,建议边开挖、边支护。

表6 边坡开挖最大水平位移变化情况表 /mm

表7 边坡开挖安全系数统计表
(3) 支护后应力分析
以边坡关键节点在水平方向发生位移突变作为模型收敛的依据。由表6可知,第1级边坡开挖后下滑力减小,安全系数提高;第2级边坡开挖后阻滑段减小,同时中部平台宽度减少,安全系数降低。由表7可知,削坡卸荷能够提高边坡稳定性,但安全系数不能满足规范要求。
3.6.3施工工程及治理后正常运行工况
(1) 边坡支护方案
通过边坡稳定性分析可知,研究区域边坡在天然状况及施工开挖存在安全隐患,为排除边坡对公园游人和坡顶居民的安全威胁,综合考虑技术和经济的合理性,采用锚杆+格梁的加固方式,布置示意图如图8所示。
锚杆布置:第1级边坡锚杆等长布置,长度为12 m直径Ø28 mm,锚杆与水平面夹角为30°,锚杆水平间距和竖直间距均为3 m,第1级边坡布置4排锚杆;第2级边坡锚杆等长布置,长度为9 m,锚杆与水平面夹角为30°,锚杆水平间距和竖直间距均为3 m,第2级边坡布置6排锚杆。
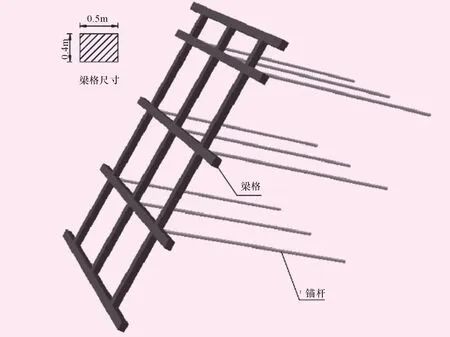
图8 锚杆+格梁布置示意图
(2) 计算模型及参数
通过数值模拟对支护后的边坡进行计算分析。在原有模型的基础上增加锚杆和格梁,梁格使用弹性材料,采用B32梁单元模拟。梁格与边坡坡面采用硬接触方式。锚杆采用Truss单元进行模拟,网格使用T2D2二节点二维桁架网格,锚杆与边坡土体采用内置接触方式进行模拟。
锚杆参数:由于本模型为二维模型,所以在选取锚杆参数时需要对锚杆参数的弹性模量进行等效转化。采用线性缩放材料属性的方法,即直接将被等效体的材料属性除以布置间距,其等效方法为刚度等效。等效之后的锚杆及各梁参数如表8所示。
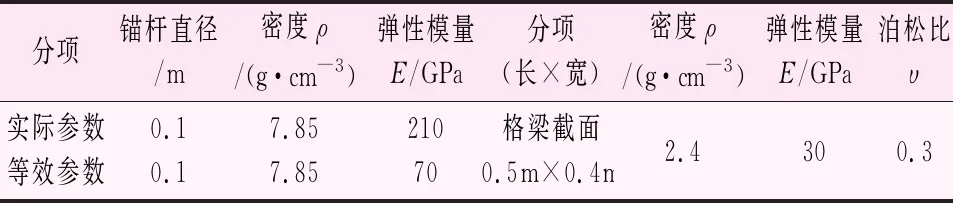
表8 锚杆计算参数表
按照边开挖边支护的方式对边坡进行支护模拟,利用Abaqus对支护过程进行数值分析得到边坡支护后的应力情况,两次支护后边坡的应力分布如图9所示:

图9 边坡支护后水平位移云图
由表9可知,通过对边坡两步支护过程中边坡应力变化分析可以发现,锚杆支护可有效减小边坡坡脚应力,提高边坡稳定性。
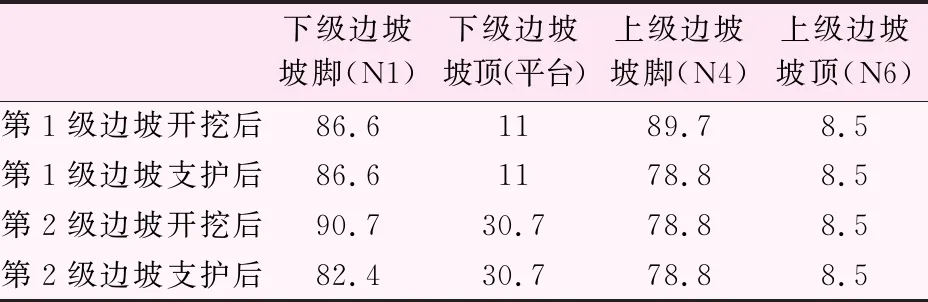
表9 边坡支护应力分布情况表 /kPa
(4) 支护后位移分析
通过边坡分级开挖及支护过程进行模拟计算,得到计算结果见图10。
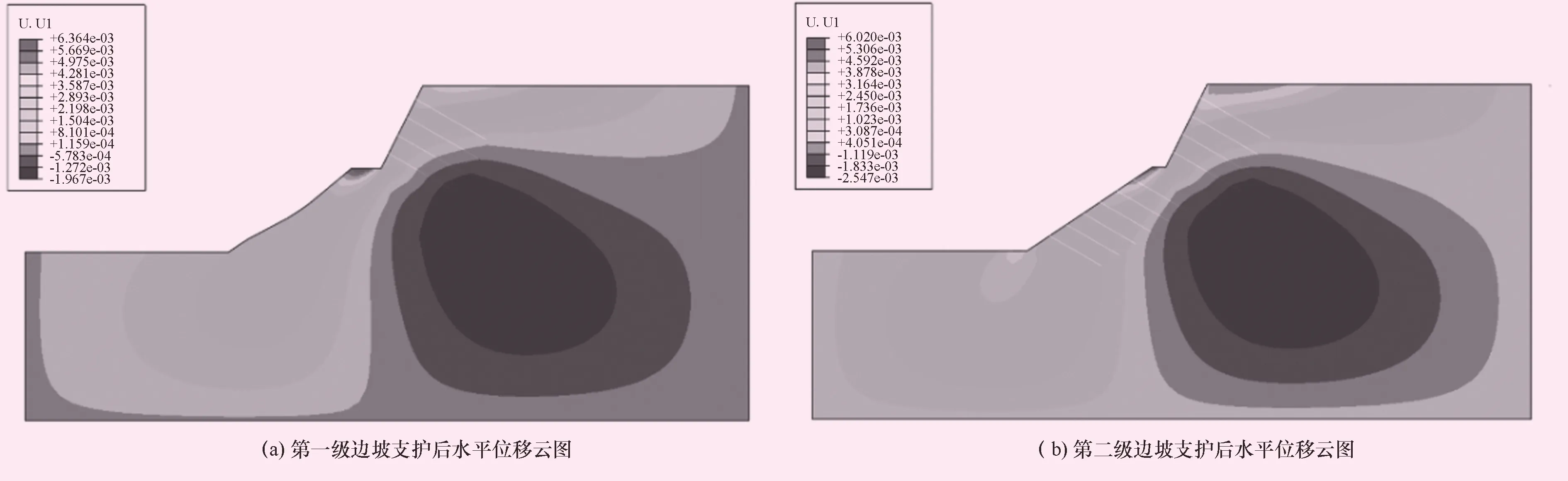
图10 边坡支护后水平位移云图
边坡支护后,水平位移计算结果如图10、表10所示。第1级及第2级边坡加固后坡脚的水平位移分别为0.5 mm、1.8 m,对比加固前边坡坡脚水平位移明显减小。

表10 边坡开挖最大水平位移变化情况表 /mm

表11 边坡加固后安全系数表
以黄土边坡特征点的水平位移发生突变作为模型收敛的评判依据,得到施工过程及支护后运行时边坡安全系数如表11所示,均满足规范要求。
综上所述,边坡加固后安全系数进一步提高,稳定性增强,加固方案合理可行。
3.6.4地震工况
对支护后边坡按照地震动峰值加速度0.15g,地震动反应谱特征周期0.35 s,Ⅶ度地震烈度进行分析计算。边坡安全系数为1.39,大于规范要求的1.05,满足设计要求。
3.6.5降雨工况
通过对边坡降雨工况下的边坡稳定性分析,计算无降雨情况、降雨无支护情况及降雨有支护情况的边坡安全分析,如图11所示。

表12 降雨情况下边坡安全系数表
通过图11与表12可以看出无支护情况下,降雨对边坡稳定影响较大,安全系数严重降低;通过锚杆+格梁支护方式有效防治边坡在降雨工况下滑动面由深层向浅层发展的过程,提高了边坡安全系数。
4 结 论
以三原县清河黄土边坡某典型断面为研究对象,根据勘探资料和试验结果,利用数值模拟法对其稳定性进行计算分析,结论如下:
(1) 黄土边坡由于垂直节理发育的特点,容易形成高陡边坡,在自然状态下保持着长期的稳定。在对长期处于稳定状态的黄土边坡进行治理时,设计坡型应尽量与原始坡型相接近,可以减少黄土边坡的开挖方量,避免过多的人为扰动。

图11 边坡滑动面位置图

图12 边坡治理后效果图
(2) 由于削坡开挖引起的边坡内部土体应力释放,使得边坡产生位移变形。数值模拟分析发现在上级边坡开挖后最大位移出现在上级边坡坡脚处,开挖之后边坡安全系数从1.15提高到1.24。在对下级边坡开挖后,边坡安全系数下降到1.2。由于下部边坡较缓,开挖之后边坡的阻滑段抗滑力减小;而且在下部开挖之后,边坡中间平台宽度减小,上级边坡土体对下级边坡坡脚的应力影响增大,所以导致边坡安全系数降低。建议采用边开挖、边支护的方法保证边坡治理施工过程安全。
(3) 通过对比开挖工况和支护后的计算结果发现,采用锚杆+格梁对黄土边坡进行支护,可以有效减小边坡水平位移。对第1级边坡进行支护后,边坡的稳定性明显提高,边坡安全系数为1.40。第2级边坡进行支护之后,边坡安全系数提高到1.46,满足规范设计要求。

