基于正交设计和灰色关联理论的混杂纤维ECC优化设计
高英力,裴甘鹏,徐艺珅,冷 政
(1.长沙理工大学交通运输工程学院,湖南 长沙 410114;2.佛山市交通科技有限公司,广东 佛山 528000;3.中建西部建设湖南有限公司,湖南 长沙 410004)
混凝土被广泛地应用在桥梁、隧道等工程基础设施中,但混凝土材料具有易裂、延性差、拉伸强度不足等问题,严重影响结构的耐久性,已成为阻碍其发展的关键工程问题[1]。工程用水泥基复合材料(Engineering Cementitious Composite,ECC)是为了克服水泥基材料易裂、脆性大、变形差等而发展的多重稳态开裂材料[2-3],其用低于2%体积掺量的高强度高弹性短纤维进行增延,极限拉应变可达到3%~5%,具有应变-硬化和稳态开裂特征[4],展现出较好的耐久性和韧性。但是ECC的高成本限制了其在建筑工程中的大规模应用。为了得到一种价格低廉、性能优越的ECC材料,部分学者开始利用混杂纤维改性ECC材料[5-6]。Y.PAN等[7]利用玻璃纤维和聚乙烯醇(Polyvinyl Alcohol,PVA)纤维混杂制备一种新型ECC机场道面材料,可以接受3万次冲击,大大延长了机场道路的服役时间。S.DEB等[8]将原纤化和单丝聚丙烯(Polypropylene,PP)纤维混杂制备了新的纤维组合ECC材料,其抗拉性能和延性得到提高,但弯曲性能提升不明显。Q.Zhang 等[9-10]将PP纤维和丙烯酸乳胶结合制备了一种超轻型ECC,通过单丝拔出试验发现聚合物可以明显提升纤维和基体的黏结性,其黏结能力相比常规ECC提升144%,能够更好地改善钢结构的耐火性及抗冲击能力。H.MA等[11]用碳酸钙晶须(Calcium Carbonate Whisker,CW)改性常规ECC,改性后的混杂纤维ECC材料较常规ECC材料抗压强度提升了23%,抗拉强度和拉应变分别提升了53%和114%。张聪等[12]通过对比钢-PVA纤维、钢-PVA-CW的力学性能,发现CW与其他纤维混杂能够提升抗拉强度和拉伸韧性。目前,混杂纤维基本聚焦于钢-PVA纤维、钢-PP纤维、玄武岩-PVA纤维,其改性是基于纤维本构关系的混杂,但是水泥基材料本身是多相态材料,内部结构复杂,其破坏过程是多层次的,纤维的加入应为多种纤维的混杂[13]。笔者在大纤维上选择了压痕处理的国产改性PP纤维(Modified Polypropylene,MPP),小纤维选取国产PVA纤维,微米级纤维选取国产碳酸钙晶须,同时为了解决PP纤维锚固力不足,选用乙烯-醋酸乙烯聚合物(EVA)进行改性,以获得一种性能优越的混杂纤维ECC材料。通过正交试验设计,探究水胶比、PVA纤维、CW及MPP纤维对HFRECC性能的影响。并在此基础上,以流动度、经时损失S30、立方体抗压强度、抗折强度、劈裂抗拉强度作为优化指标,利用组合加权-灰色关联分析方法研究对HFRECC综合性能影响的最主要因素,从而得到综合性能最优的设计参数。
1 试 验
1.1 原材料
(1)基体材料
水泥:湖南南方水泥集团有限公司生产;粉煤灰:湖南岳阳电厂生产,比表面积430 m2/kg;硅灰:比表面积1.5×104m2/kg;石英砂:0.15~0.075 mm;减水剂采用聚羧酸高效减水剂,减水率40%,掺量为胶凝材料的0.8%。
(2)纤维及聚合物材料
PVA纤维:上海影佳公司出产,表面经特殊处理,易于分散;MPP纤维:山东省凯瑞达建材有限公司生产,表面经压痕处理;CW:海峰竺有限公司生产。各纤维的基本参数如表1所示。EVA表观密度495 kg/m3,掺量为胶凝材料质量分数的4%。由于EVA的加入,会引入大量气泡,故加入胶凝材料质量分数为0.17%的有机硅高效消泡剂。

表1 纤维材料的性能参数Table 1 Physical and mechanical properties of each fiber
1.2 试验方法
笔者采用胶砂比0.36,m(水泥)∶m(粉煤灰)∶m(硅灰)=0.3∶0.6∶0.1,选取水胶比A、PVA体积分数B、CW体积分数C和MPP体积分数D为影响因素设计正交试验L9(34)(见表2)。
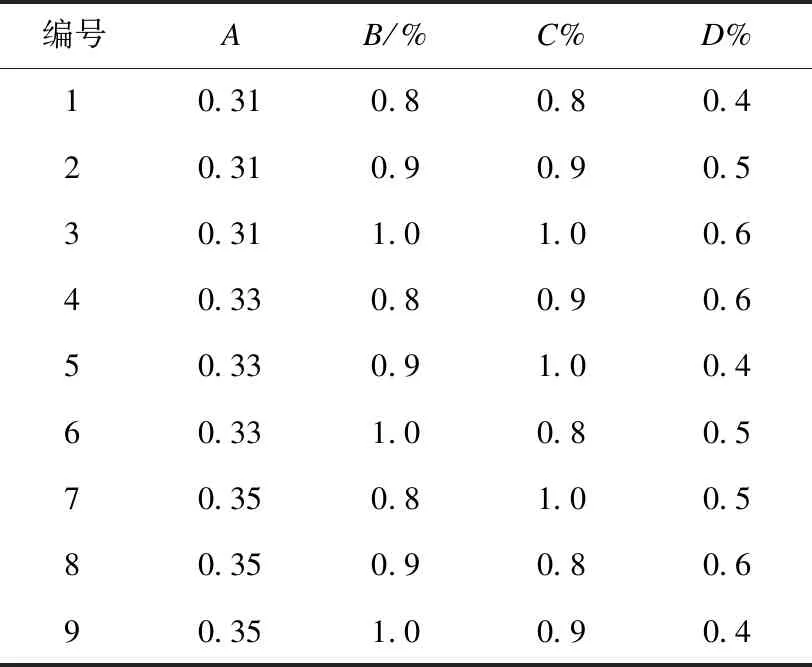
表2 正交试验方案Table 2 Orthogonal test scheme
参照国内外的ECC材料成型方式及其他纤维混凝土成型模式[14-15],将砂石、胶材、EVA、CW及适量PVA纤维进行干拌5 min,再加水、SP减水剂和消泡剂搅拌5 min,最后加入MPP纤维和剩余PVA纤维进行全拌6 min。根据《水泥胶砂流动度检测方式》(GB/T 2419—2005)测新拌混合物流动度D0,同时进行流动度的经时损失试验,分别测试10、30、60 min后对应的流动度Dn,计算对应的经时损失率Sn。将按正交表制备的HFRECC试件在温度为(20±2)℃,湿度为95%以上的标准养护室内养护,分别测试其抗压强度、抗折强度及劈裂抗拉强度。
(1)
1.3 基于正交试验的组合加权-灰色关联配合比优化设计
正交试验仅能得到单一性能最优的配合比,无法得到综合性能最佳的配合比;而利用灰色关联分析可得到综合性能最佳的配合比。但是不同指标在测试结果中的重要性不同,评价方法有两种:主观加权法和客观加权法。主观加权法很难避免评估结果的主观任意性。客观加权法包括熵权法,均方差法和偏差法,客观加权法依赖样本,不能体现各指标自身价值的重要性。因此,笔者通过主观加权法和熵权法确定相关指标的权重,结合灰色关联分析对正交试验的结果进行评价,得到综合性能最优的配合比[16-17]。
1.3.1 指标标准化处理
为了消除数据值域和单位带来的影响,将各指标数据进行标准化处理。
对于值越小,效果越优的性能指标,即效益指标进行标准化处理:
(2)
对于值越大,效果越优的性能指标,即成本指标进行标准化处理:
(3)
式中:(yi)max为第i个指标的最大值;(yi)min为第i个指标的最小值;yij为第i个评价对象的第j个指标值;rij为标准化后的指标值。
1.3.2 确定权重
(1)客观加权法-熵权法
客观赋权法认为,当各项性能指标之间的差异比较大时则认为该项性能指标对综合性能的影响比较大,因此该项性能指标所分配的权重也应该更多。
熵权法的基本思路是根据指标变异性的大小来确定客观权重,计算指标变异性即信息熵ej;根据得到的信息熵,计算得到客观权重ω1j。
(4)
(5)
式中:ej为指标j的信息熵;ω1j为第j个指标的权重。
(2)主观加权法
主观加权法ω2j通过主观判断来确定权重,考虑各指标在目标中的重要性进行主观分配权重。
(3)组合加权法
结合主观权重和客观权重计算综合权重ωj。这样既能避免仅考虑客观权重的片面性,又能够考虑主观与客观权重相比的重要性。
(6)
1.3.3 组合加权灰色关联法
对各指标赋予相应的综合权重,然后计算出最终的灰色相关度。
(7)
(8)
式中:dij为第i个评价对象的第j个指标值的灰色关联系数;r0j为第j个指标最优值;ρ为分辨系数,0<ρ<1,通常ρ取0.5。
2 结果与分析
不同配比的HFRECC流动度、立方体抗压强度fcu、抗折强度fcf和劈裂抗拉强度fts如表3所示。为探究不同因素对HFRECC性能的影响程度,利用SPSS软件对正交试验的结果进行极差和方差分析,其结果如表4、表5所示。
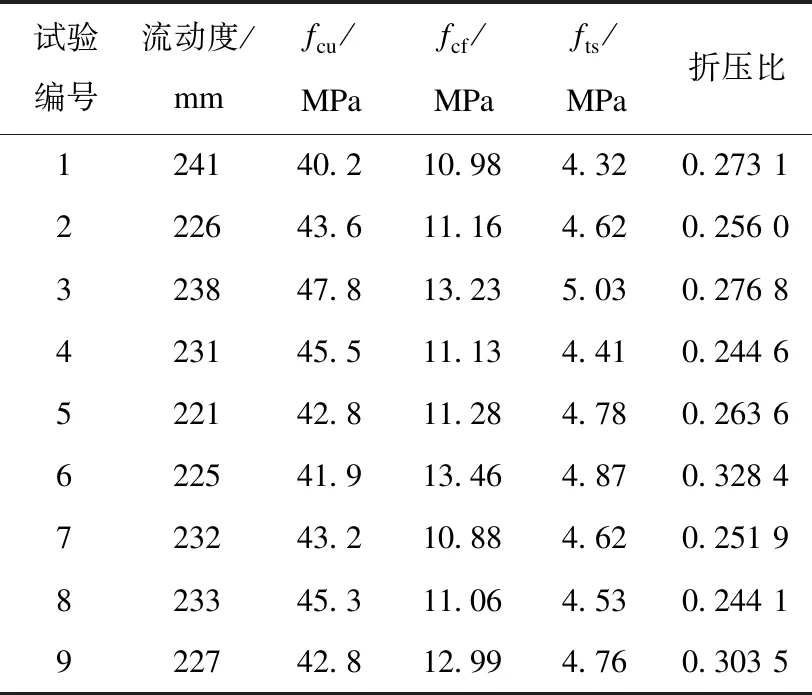
表3 正交试验结果Table 3 Results of orthogonal test
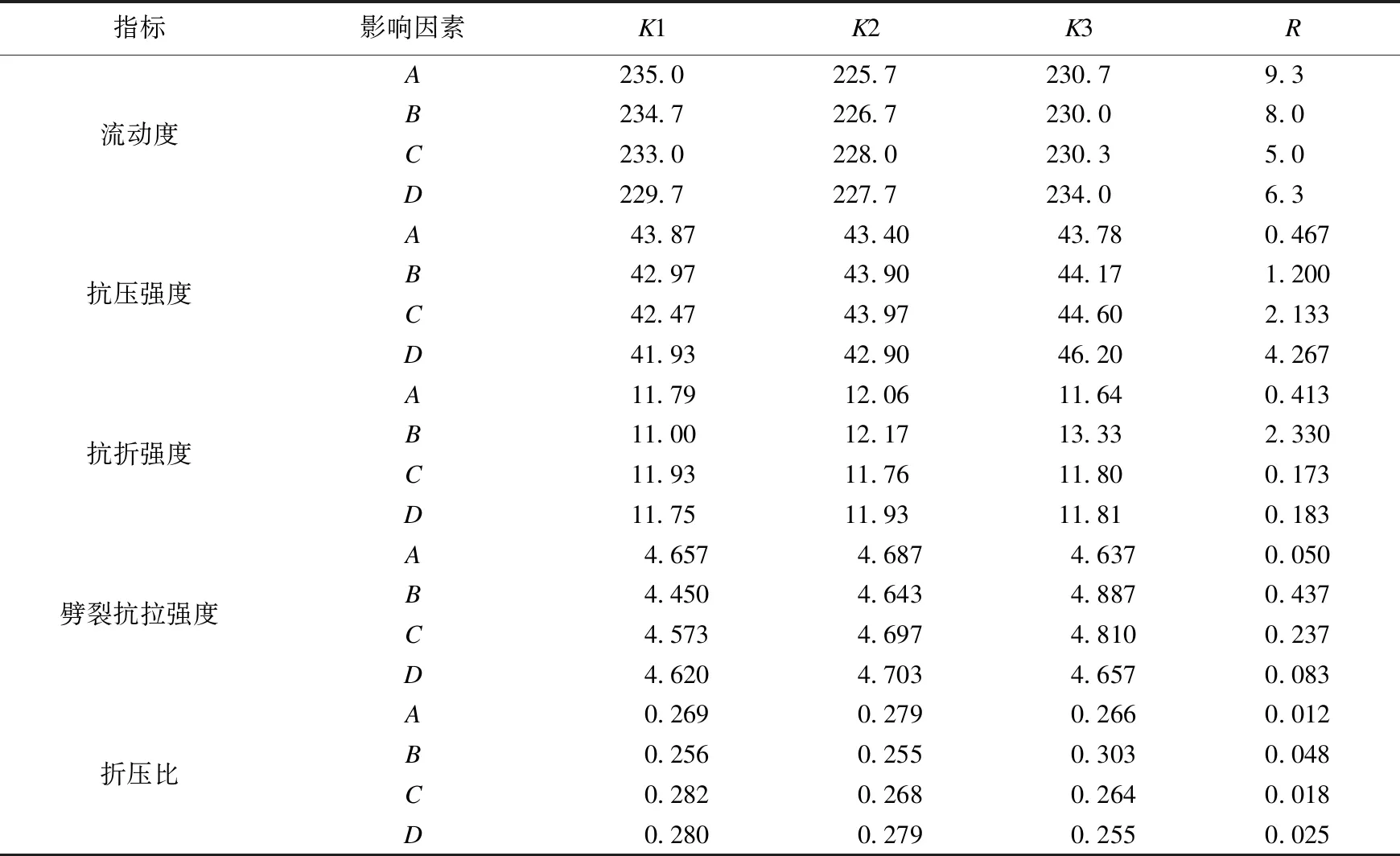
表4 试验结果极差分析Table 4 Range analysis of the test results
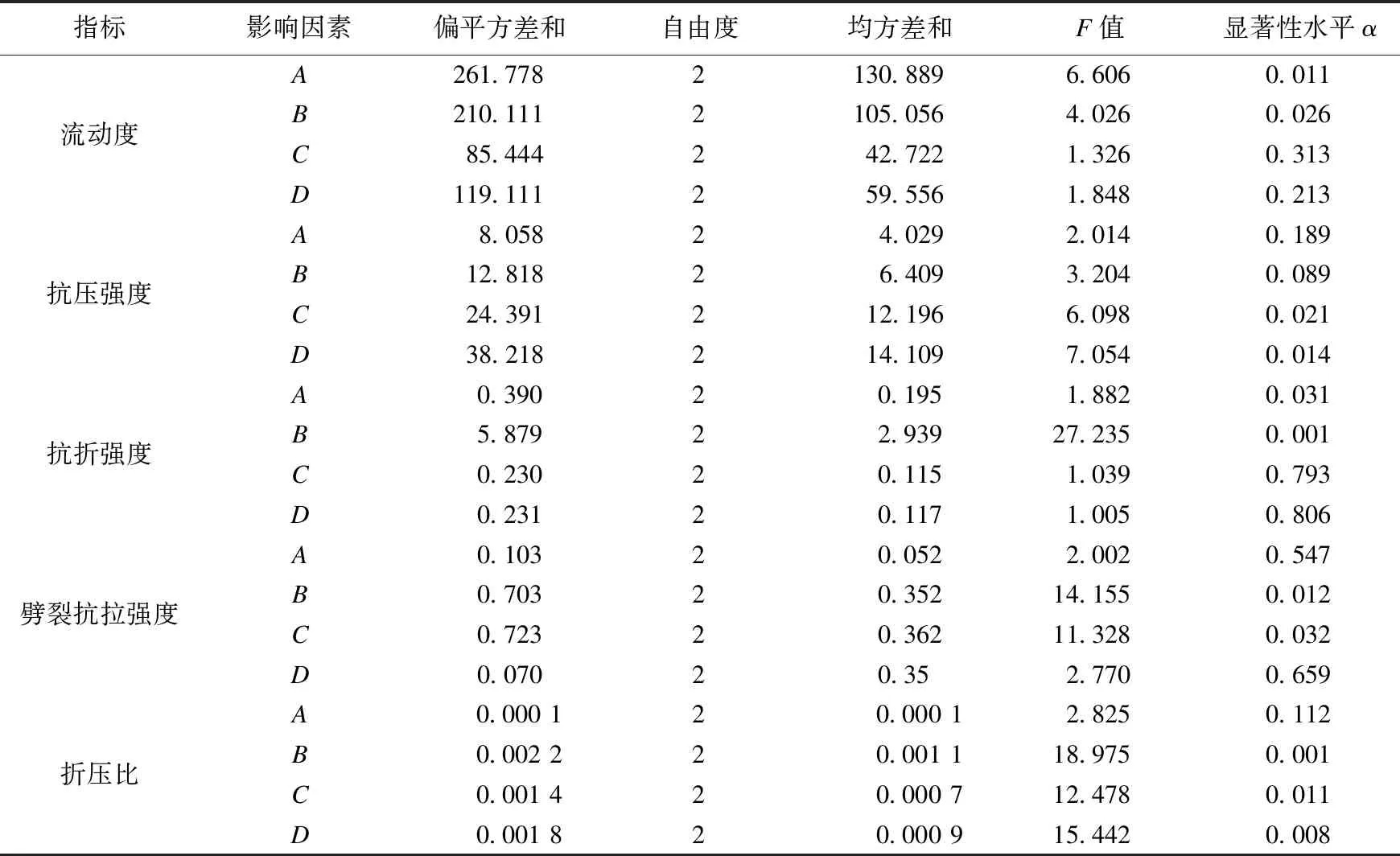
表5 试验结果方差分析Table 5 Variance analysis of the test results
2.1 流动度
从表3可知,不同配比的HFRECC流动度均大于220 mm,3种纤维的混杂提高了流动性。从表4极差分析结果可知,影响HFRECC流动度的因素大小依次为A、B、D、C,最佳组合为A1B1D3C1。随着因素水平的提升,流动度均呈先降后升的趋势,其中因素A、B随水平提升流动度变化明显,说明水胶比和PVA纤维体积分数是影响HFRECC流动度的主要因素。从表5可知,水胶比和PVA体积分数是流动性的显著性影响因素,与极差分析一致。拌合物经时损失如图1所示。在0~30 min,HFRECC流动度的经时损失率仅为1%~4%,60 min经时损失率为8%~15%,S60为S10的4~15倍,但S30仅为S10的1~3倍。建议HFRECC拌和到施工时间保持在30 min为宜,不宜超过1 h。

图1 拌合物经时损失率Fig.1 Rate of fluidity loss over time
2.2 立方体抗压强度
由表4可知,HFRECC试件立方体抗压强度影响因素的主次顺序依次为D,C,B,A,最优配比为D3C3B3A1。A从0.31增加至0.33,fcu降低1.1%;从0.31增加至0.35,fcu降低0.2%,说明水胶比对抗压强度的影响并不明显。B从0.8%增加至0.9%,fcu提高2.2%;从0.8%增加至1.0%,fcu仅提高2.8%。C从0.8%增加至0.9%,fcu提高3.5%;从0.8%增加至1.0%,fcu提高5.0%。D从0.4%增加至0.5%,fcu提高2.3%;从0.4%增加至0.6%,fcu提高10.2%。随着MPP、CW及PVA掺量的增加,HFRECC的抗压强度有所提高,且因素C、D是其抗压强度的主要影响因素。由表5可知,因素C和D的显著性水平小于0.05,因此CW体积分数和MPP纤维体积分数是HFRECC抗压强度的显著性影响因素,结果与极差分析一致。
2.3 抗折强度
从表4可知,HFRECC抗折强度影响因素的主次顺序依次为B,A,D,C,仅从抗折强度考虑,最优组合为B3A2C1D2。A从0.31增加至0.33,fcf增加2.3%;A从0.31增加至0.35,fcf降低1.2%,说明不能仅从降低水胶比来提升抗折强度。B从0.8%增加至0.9%,fcf提高10.6%;从0.8%增加至1.0%,fcf提高21.2%。C从0.8%增加至0.9%,fcf降低1.4%;从0.8%增加至1.0%,fcf降低1.1%,说明CW的掺入会影响抗折强度,CW不宜过量。D从0.4%增加至0.5%,fcf提高1.5%;从0.4%增加至0.6%,fcf提高0.5%。从抗折试验可知PVA纤维对试件抗弯起主要作用,其他纤维的加入起到协同增韧作用。PVA纤维体积分数对HFRECC抗折强度的影响程度远大于水胶比、MPP纤维体积分数及CW体积分数,其中后二者对抗折强度影响程度相近。由表5可知,A的显著性水平小于0.05,B的显著性水平小于0.01,结果表明PVA纤维体积分数是HFRECC抗折强度的极显著因素,水胶比是HFRECC抗折强度的显著因素。
2.4 劈裂抗拉强度
由表4可知,各因素对HFRECC劈裂抗拉强度的影响程度从大到小依次为B,C,D,A,最优组合为B3C3D2A2。B从0.8%增加至0.9%,fts提高4.3%;从0.8%增加至1.0%,fts提高9.8%。C从0.8%增加至0.9%,fts提高2.7%;从0.8%增加至1.0%,fts提高5.2%。D从0.4%增加至0.5%,fts提高1.8%;从0.4%增加至0.6%,fts提高0.8%。A从0.31增加至0.33%,fts提高0.9%;从0.31增加至0.35,fts降低0.4%。PVA纤维体积分数对HFRECC劈裂抗拉强度的影响程度与抗折强度相近。从表5中劈裂抗拉强度方差分析可知,PVA纤维体积分数和CW体积分数为HFRECC劈裂抗拉强度的显著性影响因素。
2.5 折压比
由表4可知,4个因素对折压比的影响程度从大到小依次为B,D,C,A,仅从折压比考虑,较优组合为B3D1C1A2。从表5中HFRECC折压比的方差分析可知,PVA纤维体积分数、CW体积分数和MPP纤维体积分数是折压比的显著性影响因素,PVA纤维体积分数对折压比贡献远大于CW体积分数和MPP纤维体积分数。
3 基于正交试验的组合加权-灰色关联配合比优化设计
以流动度、经时损失S30、立方体抗压强度、抗折强度、劈裂抗拉强度作为优化指标,通过组合加权-灰色关联法对正交试验的结果进行处理,获得最佳的配合比设计参数。
经时损失S30是成本指标,初始值由式(3)处理,而其他4个指标是效益指标,初始值由式(2)处理。并根据式(4)和式(5),计算出5个指标的客观权重。
W1j=[0.145 7 0.136 4 0.130 9 0.380 4 0.206 6]
工作性能与力学性能同等重要,工作性能由两个指标代表,力学性能由3个指标代表,这5个指标的主观权重设置结果为
W2j=[0.250 0 0.250 0 0.166 7 0.166 7 0.166 6]
根据式(6),流动度、经时损失S30、立方体抗压强度、抗折强度及劈裂抗拉强度的组合权重计算结果为
Wj=[0.191 5 0.179 3 0.114 7 0.333 4 0.181 1]
根据式(7)和式(8),计算出不同测试方案的灰度相关度。灰色关联度随各因素变化而变化的趋势如图2所示。各因素关联度分别为HFRECC综合性能最佳的组合为水胶比0.31,PVA体积分数1.0%,CW分数0.8%,MPP体积分数0.6%。
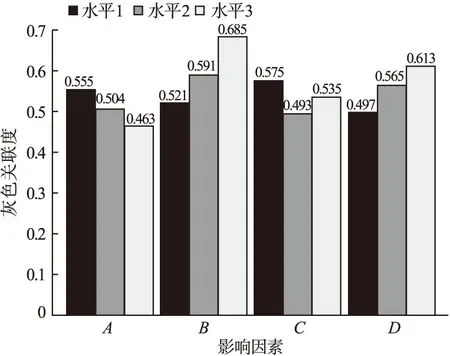
图2 基于灰色关联分析的参数优化Fig.2 Optimization of mix proportion parameters based on grey relational analysis
由组合加权-灰色关联分析得到最优配比不在正交试验组中,故按最优配比重新制作试件R,测其工作性能及力学性能。同时为了验证试验的可行性按照日本可乐丽公司推荐ECC配方设置了试验组L,其胶砂比0.36,水胶比0.31,m(水泥)∶m(粉煤灰)=0.5∶0.5,日本PVA掺量为2%,R组和对照组L的结果如表6所示。在此配合比下,流动度为238 mm,仅次于最大组(241 mm),经时损失S30为3%,相较于基准组L,最优配比R的力学性能有很大提高,抗压强度提高了23%,抗折强度提高了42.4%,劈裂抗拉强度提高了34.4%,折压比提高了17.8%,流动度提升了28.6%,抗折强度及劈裂抗拉强度的大幅度增长说明改性后的ECC变形能力有了较好的改善。

表6 最优组合R组及对照组L的工作性能及力学性能Table 6 Work performance and mechanical properties of optimal mixtures of R and control group L
4 结 论
(1)进行混杂纤维ECC的正交试验,不同配比拌合物流动度均大于220 mm,远高于基准组,拌合物的流动性有较好地改善。且HFRECC拌和到施工时间保持在30 min为宜,不宜超过1 h。
(2)PVA纤维体积分数分别是HFRECC流动度和抗折强度、劈裂抗拉强度的显著性影响因素,CW体积分数分别是抗压强度、劈裂抗拉强度的显著性影响因素,MPP纤维体积分数是抗压强度的极显著影响因素,综合分析其工作性能,3种纤维混杂对HFRECC强度的影响表现正混杂效应。
(3)通过组合加权-灰色关联度分析,解决了多因素多水平正交试验确定最优参数时主观性大的问题,实现对混杂纤维ECC的配合比综合优化设计。

