新疆果园深施散体厩肥离散元参数标定研究

韩树杰 戚江涛 坎 杂 李亚萍 蒙贺伟

(1.石河子大学机械电气工程学院， 石河子 832003； 2.农业农村部西北农业装备重点实验室， 石河子 832003)

0 引言

新疆地区厩肥资源较为丰富，施用厩肥可促进果园土壤微生物的生命活动，对提高土壤肥力、改善土壤结构、补充土壤养分和创造良好的土壤生态环境具有重要作用[1-3]。

近年来，随着计算机技术的发展，离散元法(Discrete element method, DEM)在农业装备研究上应用越来越广泛[4-8]。利用离散元法全面、系统研究散体物料和机械装置之间的相互作用机理和物料的运动状态，不仅可以优化机械装置的结构参数和工作参数，而且可以提高研发效率、改善机械作业性能、节约成本。物料离散元参数标定是研究物料与机械装置之间相互作用的基础。GRIMA等[9]利用崩塌试验中的颗粒堆休止角对干颗粒在离散元仿真中所需滚动摩擦因数进行了标定；BOAC等[10]运用离散方法模拟了精选油籽颗粒的材料和相互作用特性；温翔宇等[11]对颗粒肥料进行离散元仿真，标定了颗粒肥的摩擦因数；袁全春等[12]对有机肥散体颗粒离散元模型进行参数标定，仿真休止角与实际休止角的相对误差仅为0.42%；罗帅等[13]基于JKR粘结模型标定了蚯蚓粪基质的离散元参数，休止角仿真结果与实际试验结果较为接近；文献[14-17]分别对粘性土壤、沙土颗粒土壤的模型参数进行了标定，结果表明，虚拟仿真结果与实测值之间差异较小。

本文在以上研究基础上，以新疆果园深施散体厩肥为研究对象，采用仿真试验与物理试验相结合的方法，对散体厩肥的离散元参数进行标定，从而获得散体厩肥的离散元模型，以期为全面、系统研究肥料和施肥装置之间的相互作用机理以及物料的运动状态提供参考。

1 材料与方法

1.1 试验材料

试验所用厩肥为新疆生产建设兵团第八师一二一团葡萄园用厩肥，由纯牛粪发酵，发酵时间为3～4个月。前期试验结果表明，为保证施肥机作业性能，提高施肥机施肥均匀性和稳定性，施肥前需对厩肥进行粉碎处理。用环刀法测定所选厩肥的密度；选取500 g厩肥作为试验样本，使用土壤标准粒径筛(筛孔直径0.25～5 mm)确定其粒径分布情况；用MH45型含水率测定仪(质量测量精度0.001 g,含水率测量精度0.01%)测定厩肥的含水率；堆积角试验中所用钢板材质为45号钢，参照文献[18-20]确定所选材料的泊松比、剪切模量，材料的基本性质如表1所示，本征参数如表2所示。

表1 厩肥基本性质Tab.1 Basic properties of manure

表2 厩肥、钢本征参数Tab.2 Intrinsic parameters of manure and steel plate

1.2 试验方法

肥料颗粒的自然堆积角能反映其流动、摩擦等特性[21],本文采用物理试验与仿真试验相结合的方法[22-23]对厩肥离散元模型参数进行标定，采用注入法对厩肥进行堆积角试验，并在EDEM离散元仿真软件中进行仿真，应用Design-Expert 8.0.6软件进行Plackett-Burman多因素显著性筛选试验与分析，得出对堆积角有显著性影响的参数；在此基础上，通过Box-Behnken响应面分析法建立并优化厩肥堆积角与显著性参数的回归模型，以实际堆积角为目标值对回归方程求解寻优，得到显著性参数最优值。最后在最优参数下进行仿真试验，对比厩肥仿真堆积角和实际堆积角，验证标定的厩肥离散元模型参数的准确性。

1.3 物理模型

结合文献[24-26]对堆积角的相关研究，试验参照GB 11986—89/ISO 4324—1977《表面活性剂粉体和颗粒休止角的测量》，采用注入法测量散体厩肥的堆积角，测量装置如图1所示，漏斗下口内径为10 mm，锥度为60°，托盘直径为100 mm，高度为25 mm，漏斗的下端口与托盘上表面距离为75 mm。试验时，漏斗中的厩肥颗粒经漏斗口落于托盘上，最终在托盘上形成稳定的颗粒堆，在侧面对堆积角拍照，采用Matlab对图像进行处理以获得厩肥颗粒的堆积角。重复5次试验取其平均值，试验得到厩肥的堆积角为35.47°。

2 厩肥堆积角仿真试验

2.1 颗粒间接触模型

在EDEM接触模型理论中，Hertz-Mindlin with JKR Cohesion模型是一个凝聚力接触模型，该接触模型在Hertz接触理论的基础上结合JKR理论，考虑湿颗粒间粘结力对颗粒运动的影响，适用于模拟颗粒间因水分发生明显粘结和团聚的物料[14]。在该模型中，法向弹性接触力的实现基于Johnson-Kendall-Roberts理论，切向弹性力、法向耗散力和切向耗散力均与Hertz-Mindlin(no slip)接触模型中的计算方法一致，在Johnson-Kendall-Robert理论中，JKR法向弹性力的实现基于重叠量δ、相互作用参数和表面能。计算式为

(1)

(2)

其中

(3)

(4)

式中FJKR——JKR法向弹性力，N

α——相互接触2个颗粒的接触圆半径，m

γ——表面能，N/m

E*——等效弹性模量，Pa

R*——等效半径，m

Ei、Ej——相互接触2个颗粒的弹性模量，Pa

vi、vj——相互接触2个颗粒的泊松比

Ri、Rj——相互接触2个颗粒的半径，m

当γ=0时，力变为Hertz-Mindlin法向力

(5)

即使颗粒并不是直接接触，该模型也提供吸引凝聚力，颗粒间具有非凝聚力的最大间隙为

(6)

(7)

式中δc——颗粒间具有非凝聚力时的法向最大间隙，m

αc——2个颗粒的接触半径，m

当颗粒并非实际接触并且间隙小于δc时，凝聚力达到最大值

(8)

摩擦力的计算和Hertz-Mindlin(no slip)接触模型不同，其取决于JKR法向力的正向排斥部分。因此，该模型在接触力的凝聚力分量更大时提供一个更大的摩擦力。

因此，经过处理后的厩肥具有散粒体的物料特性，厩肥颗粒之间受水分子和化学物质的影响也具有粘结力特性。为了更准确地模拟厩肥的真实状态，本文选择Hertz-Mindlin with JKR Cohesion 模型进行仿真模拟。

2.2 几何模型建立

在仿真过程中，颗粒和装置模型对仿真结果有很大的影响，在保证仿真模型尺寸与物理模型一致的基础上，建立了简化的厩肥和漏斗装置模型。经过粉碎处理的散体厩肥颗粒近似球形，将厩肥颗粒模型设置为球形。在SolidWorks软件中根据物理试验模型建立仿真模型，把模型转换为STL格式，导入EDEM 2.7软件中作为漏斗装置仿真模型，本文采用EDEM软件内置的Hertz-Mindlin(no slip)接触模型作为颗粒与装置之间的接触模型，颗粒模型及漏斗模型如图2、3所示。

2.3 仿真参数设置

根据试验所测定的厩肥颗粒粒径分布范围，为确保仿真结果准确性的同时提高仿真效率，仅生成粒径分布占比较大区间的颗粒。在EDEM中采用随机分布，将生成的球颗粒半径限制在0.5～1.25倍的初始球半径之间。仿真中，动态生成漏斗中颗粒，在漏斗正上方建立颗粒工厂，设置为虚拟，生成总质量为0.6 kg，生成速率为0.2 kg/s，数据保存时间间隔为0.01 s，固定时间步长是瑞利时间步长的20%，网格尺寸取2倍最小球形单元尺寸。基于EDEM内嵌Hertz-Mindlin with JKR Cohesion模型进行厩肥接触参数的仿真标定，其模型参数(JKR表面能)是表征所研究物料含水率效果的重要参数。通过大量预试验确定了JKR表面能的取值范围。综合对比文献[12,18-20]中所研究肥料、土壤与本文所研究厩肥特性的差异，确定厩肥仿真接触参数的取值范围，如表3所示。

表3 仿真参数取值范围Tab.3 Simulation parameters

2.4 仿真试验与结果分析

2.4.1Plackett-Burman筛选试验

Plackett-Burman筛选试验通过考察目标响应与各因子间的关系，比较各个因子2水平间的差异性来确定因子显著性。本文Plackett-Burman试验设计以厩肥堆积角为响应值，对仿真接触参数及接触模型参数进行筛选。试验接触参数高水平设置为低水平的2倍，根据文献[13-14]中因素高低水平取值方法，确定本文因素水平如表4所示。

表4 因素水平Tab.4 Factors and levels

Plackett-Burman试验方案及结果如表5所示，A～G为因素水平值，H～L为空白列，利用Design-Expert 8.0.6软件[27-28]对该结果进行方差分析，得到接触参数和接触模型参数显著性如表6所示。由表6可知，JKR表面能、厩肥-厩肥恢复系数、厩肥-钢恢复系数的P<0.05，对厩肥堆积角的影响显著；而其他参数的P>0.05，对厩肥堆积角影响不显著。

表5 Plackett-Burman试验方案及结果Tab.5 Scheme and results of Plackett-Burman test

表6 Plackett-Burman试验结果显著性分析Tab.6 Significance analysis of Plackett-Burman test results

为方便后续试验，在Box-Behnken试验[29-30]中只考虑3个影响显著的参数，不显著因素取值分别为厩肥-厩肥静摩擦因数0.65、厩肥-厩肥滚动摩擦因数0.3、厩肥-钢静摩擦因数0.53、厩肥-钢滚动摩擦因数0.3，进行响应面试验设计。

2.4.2Box-Behnken响应面试验及回归模型

根据响应面设计原理，选取显著性参数的低、中、高3个水平进行试验设计，试验选取5个中心点对误差进行评估。Box-Behnken试验参数取值如表7所示。

表7 Box-Behnken试验参数取值Tab.7 Parameter value of Box-Behnken test

Box-Behnken试验方案及结果如表8所示，重点考察3个对厩肥堆积角影响显著参数，即JKR表面能、厩肥-厩肥恢复系数、厩肥-钢恢复系数。应用Design-Expert软件建立堆积角θ与3个显著性参数的二阶回归方程为

θ=30.92+1.75A+0.88D+3.23G-0.21AD- 1.07AG+0.46DG-0.63A2+0.041D2+0.69G2

(9)

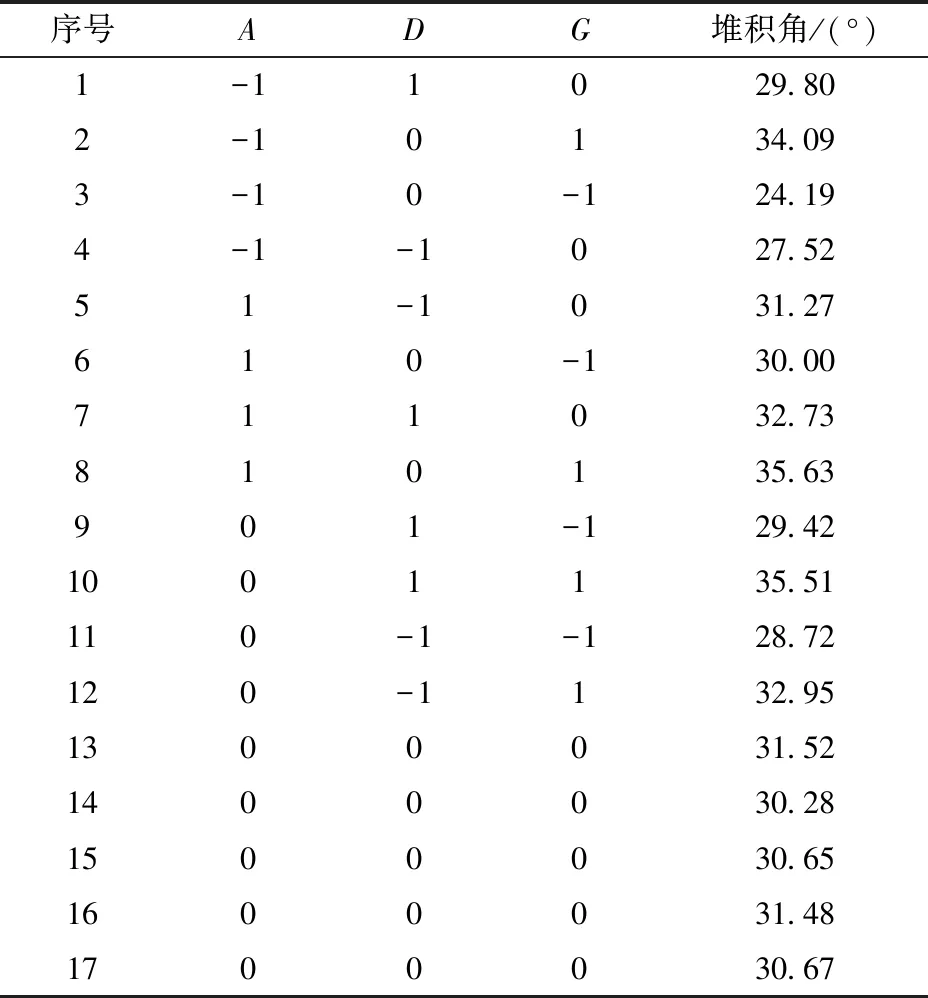
表8 Box-Behnken试验方案及结果Tab.8 Design and results of Box-Behnken test

Box-Behnken试验模型方差分析结果如表9所示，由表9可知，该拟合模型P=0.000 3，拟合度较好；厩肥-厩肥恢复系数(A)、JKR表面能(G)P值均小于0.01；厩肥-钢恢复系数(D)、厩肥-厩肥恢复系数和JKR表面能交互项(AG)P值均小于0.05，说明各个参数对堆积角的影响显著，表明回归模型的有效性。失拟项P=0.114 7>0.05，表明所得回归方程与实际拟合中非正常误差所占比例小，没有弯曲失拟现象发生，拟合性较好。试验中变异系数为2.65%，说明试验有较高的可靠性。决定系数为

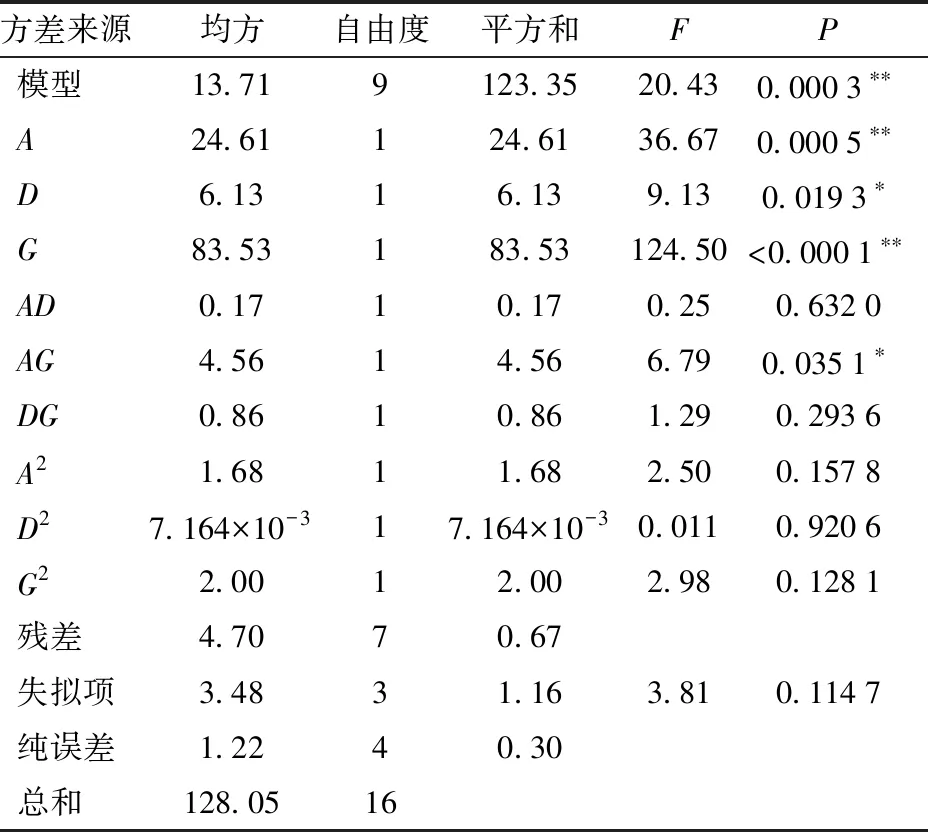
表9 Box-Behnken试验模型方差分析Tab.9 ANOVA of quadratic polynomial model of Box-Behnken test

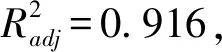
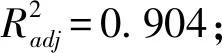
θ=30.97+1.75A+0.88D+3.23G-1.07AG

(10)

表10 Box-Behnken试验优化回归模型方差分析Tab.10 ANOVA of modified model of Box-Behnken test

2.4.3回归模型交互效应分析

根据优化回归模型方差分析结果，可知厩肥-厩肥恢复系数和JKR表面能的交互项(AG)对厩肥的堆积角影响显著(P<0.05)。当厩肥-厩肥恢复系数为0.35时，应用Design-Expert软件绘制厩肥-厩肥恢复系数和JKR表面能交互作用(AG)的响应曲面(图4)，可以直观地看出两个参数之间的交互效应。由AG曲面可知，随着两个参数取值的增加，厩肥堆积角均呈现上升趋势，相对于厩肥-厩肥恢复系数(A)，JKR表面能(G)的效应面曲线比较陡，表明其对堆积角影响较为显著。

3 最佳参数组合确定与仿真验证

应用Design-Expert软件对优化后的回归方程进行寻优求解，当JKR表面能为0.02 J/m2，厩肥-钢恢复系数为0.49，厩肥-厩肥恢复系数为0.34，其余非显著性参数选取中间水平(厩肥-厩肥静摩擦因数0.65，厩肥-厩肥滚动摩擦因数0.3，厩肥-钢静摩擦因数0.53，厩肥-钢滚动摩擦因数0.3)时，仿真结果与实际堆积角相对误差最小。为验证最优参数组合的准确性，采用上述参数值，其他参数设置不变，应用EDEM 2.7软件进行堆积角仿真试验，3次重复仿真所得厩肥堆积角分别为34.8°、35.0°、33.7°。厩肥堆积角3次平均值为34.5°。与厩肥实际堆积角35.47°的相对误差为2.73%，并且，从图5a可以直观看出，利用标定后的厩肥参数得到的堆积边界与厩肥物理试验堆积结果比较接近，说明所得厩肥参数的最优值准确可靠，仿真试验与物理试验的对照如图5b、5c所示。

4 结论

(1)通过Plackett-Burman筛选试验，得到对厩肥堆积角具有显著影响的接触参数和接触模型参数为厩肥-厩肥恢复系数、厩肥-钢恢复系数、JKR表面能，而厩肥-厩肥的静摩擦因数和滚动摩擦因数、厩肥-钢的静摩擦因数和滚动摩擦因数对堆积角无显著性影响。

(2)通过Box-Behnken响应曲面试验，得出对厩肥堆积角影响显著的参数，建立显著性参数与堆积角之间的二次回归模型，并对其进行优化，根据其方差分析得出，3个显著性参数的一次项(厩肥-厩肥恢复系数、厩肥-钢恢复系数、JKR表面能、厩肥-厩肥恢复系数和厩肥表面能的交互项对厩肥堆积角影响显著。

(3)通过对优化后的回归模型求解可知，当JKR表面能为0.02 J/m2、厩肥-钢恢复系数为0.49、厩肥-厩肥恢复系数为0.34，非显著性参数选取中间水平时，仿真试验和物理试验得到的厩肥堆积角无显著性差异(P>0.05)，说明采用响应面方法分析标定厩肥接触参数和接触模型参数可行。