一种基于SVDCKF的无人机动态自适应航姿算法
杨跃, 刘小雄, 章卫国, 刘旭航, 郭一聪
(西北工业大学 自动化学院, 陕西 西安 710129)
近些年来,无人机应用在许多领域,如空中监视[1]、三维地图重构[2]、搜索救援[3]等。其中,航姿参考系统(attitude and heading reference systems,AHRS)作为无人机自主飞行系统的关键部分,主要由航姿传感器(陀螺仪、加速度计、磁力计)和微处理器组成,利用传感器融合算法解算无人机航姿,并且无需其他传感器辅助。本文重点是对低成本航姿传感器的小型无人机航姿解算进行研究。
目前,小型无人机航姿解算算法主要包括互补滤波[4]、卡尔曼滤波[5]等。其中,互补滤波依靠传感器之间的频率互补特性,融合传感器数据来计算航姿。梯度下降滤波通过一种迭代的方式寻找最优值,具体的实现过程是根据目标函数斜率的负方向搜索解。不过这两种方法都没有考虑低成本航姿传感器噪声对航姿解算精度的影响。相较于互补滤波和梯度下降滤波,卡尔曼滤波是将带有噪声的多种传感器进行融合的线性最小方差估计方法,同时在建模过程中也会考虑噪声的影响。通常在高斯噪声分布系统中,卡尔曼滤波被看作是一种最佳估计器,经常用作处理线性系统模型。不过在实际应用中,无人机航姿系统是非线性模型。此时卡尔曼滤波处理非线性模型会导致航姿解算精度下降,甚至发散,因此一些改进的非线性卡尔曼滤波[6]逐渐被用作无人机航姿解算。针对无人机航姿解算问题,文献[7]提出了一种扩展卡尔曼四元数航姿算法,使用扩展卡尔曼滤波对建立的非线性航姿模型进行处理,并且将四元数和陀螺仪随机偏差作为状态估计参数。文献[8]利用多级可变扩展卡尔曼滤波算法,使用低成本惯性器件、磁力计以及GPS导航系统等多种传感器,设计出一种可以实时估计无人机航姿的滤波估计器。 扩展卡尔曼滤波是一种对非线性函数进行一阶泰勒展开的近似方法,这样会使得模型存在舍入误差。所以一些基于确定采样型的非线性卡尔曼滤波相继被提出,主要包括无迹卡尔曼滤波[9]、容积卡尔曼滤波[10]、粒子滤波[11]等。文献[12]提出了一种基于自适应无迹卡尔曼滤波的四元数航姿滤波算法,相比于扩展卡尔曼滤波,该算法可以将非线性航姿模型精确到二阶及二阶以上的精度,并且无需对模型进行雅可比矩阵显式计算。容积卡尔曼滤波采用容积加权采样点,对非线性函数模型的逼近可以达到三阶及三阶以上,精度较无迹卡尔曼滤波进一步提高。粒子滤波是一种基于贝叶斯采样估计的重要性序列采样滤波方法,虽然与无迹卡尔曼滤波和容积卡尔曼滤波相比精度更高,但是粒子滤波计算量大,实时性较差。同时在滤波过程中,容易出现粒子退化问题,导致滤波器发散。
实际上,当无人机在进行飞行时,航姿模型统计特性会受到一些不确定因素的影响,导致航姿解算的鲁棒性下降。文献[13]提出一种新的卡尔曼航姿滤波用于估计姿态四元数,同时设计了一种自适应滤波方法用于减少系统噪声特性中的模型误差,提高了滤波抗扰性。文献[14]设计了自适应增益方法来调节航姿测量噪声方差,并且消除了不确定性误差的影响,解算出可靠的无人机航姿。
本文首先建立了无人机非线性航姿系统模型,将姿态四元数和航姿传感器随机偏差作为状态向量估计参数。针对航姿模型系统的非线性和滤波过程中协方差矩阵出现的非正定问题,设计了奇异值容积卡尔曼滤波,提高了航姿解算精度。考虑到飞行过程中三轴加速度对无人机航姿解算的影响,设计了一种动态自适应调节因子,改善了加速度测量噪声方差。最后通过仿真和实验结果表明该算法可以提高无人机航姿解算的精度和鲁棒性。
1 航姿数学模型
1.1 四元数姿态更新模型
在无人机捷联姿态表示方法中,通常用单位四元数进行姿态更新和刚体转换的快速计算。

(1)
式中:qw是四元数实部;qv是四元数虚部且有qv=qxi+qyj+qzk;θ是旋转角;e是旋转轴且e=[ex,ey,ez]T。
四元数连续乘法运算可以定义如下
(2)式和(3)式中,⊗表示四元数乘法算子。q-1是q的可逆四元数,同时四元数必须满足(4)式的正交原则。

(4)
本文利用单位四元数进行无人机姿态更新,对四元数姿态微分方程使用一阶毕卡迭代法进行求解,并给出离散模型。
q(tk)=q(tk-1)⊗q(Δt)
(5)
式中:q(tk)和q(tk-1)分别是在时间点tk-1和tk的单位四元数;q(Δt)由陀螺仪三轴角速度进行更新。
(6)
式中,Ωw是陀螺仪三轴角速度的反对称矩阵,具体形式如下
(7)
式中,w=[wx,wy,wz]T是陀螺仪在机体系下的三轴角速度。
(8)
1.2 航姿传感器模型
航姿解算离不开航姿传感器的测量值。本文使用低成本航姿传感器,主要包括陀螺仪,加速度计和磁力计。这些传感器固联在小型无人机机体重心,并且传感器的三轴之间在理想条件下相互正交。
(9)

1.3 航姿问题表述
无人机航姿模型在实际情况中是非线性系统,因此本文建立了高斯离散状态下航姿非线性系统模型。
(10)
式中:xk是航姿状态估计参数;f(·)是非线性动力学函数;vk-1是航姿传感器输入参数;zk是航姿观测参数,h(·)是非线性观测函数。其中,mk-1和nk分别是系统动态噪声和观测噪声,假设两者都是零均值高斯白噪声且互不相关。
1.4 非线性航姿模型
对于无人机航姿解算,建立无人机航姿模型是非常有必要的。根据对四元数姿态更新、航姿传感器模型以及航姿问题的分析,本文设计了一种非线性四元数航姿模型系统。(11)式是航姿系统动力学方程,其中航姿状态参数x(tk)包括四元数q(tk)以及航姿传感器偏差[bω(tk),ba(tk),bm(tk)]T。
(11)
式中,mq(tk-1),mw(tk-1),ma(tk-1)和mm(tk-1)是系统过程噪声且满足以下条件
在系统观测模型中,对于加速度计和磁力计数据采样频率不一致的问题,可以考虑单独设计相应航姿传感器系统观测模型。(12)式是观测传感器为加速度计的非线性观测方程。
(12)

在解算无人机偏航角时,使用磁力计测量当地磁场强度数值,并且将计算得到的航向角作为观测值。(13)式和(14)式为偏航角非线性观测方程。
(13)
zm(tk)=atan2(mx,my)+nm(tk)
(14)

2 非线性航姿SVDCKF滤波
针对非线性航姿滤波问题,本文采用CKF滤波方法,较之于EKF和UKF有更好的解算精度。利用Cholesky 分解状态协方差矩阵P且P=UTU,U是三角矩阵。不过使用Cholesky分解会出现一些问题:
1) Cholesky分解状态协方差矩阵P时,P必须满足正定或者对称正定的性质,这样做限制了P的取值范围,导致航姿解算不稳定;
2) 状态协方差矩阵在航姿滤波算法运行期间可能会成为稀疏矩阵,破坏了Cholesky分解对P的要求。
因此本文利用奇异值分解(singular value decomposition,SVD)来代替Cholesky分解,使得状态协方差矩阵P可以克服上述问题。
P=USVT
(15)
(15)式为奇异值分解,其中P为m×m维的任意矩阵,U和V是单位正交矩阵。S是对角矩阵,并且S矩阵对角线上的元素称为“奇异值”。
(16)
将SVD奇异值分解和CKF滤波结合,设计一种航姿SVDCKF滤波算法,图1是非线性航姿滤波框图,具体步骤如下:
(17)

(18)
式中:n是滤波状态维数;m是cubature采样点个数。本文航姿状态维数n=13,cubature采样点个数m=26。
step 2 航姿滤波状态预测。
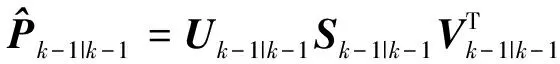
(19)
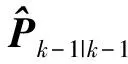
计算cubature采样点Xi,k-1|k-1(i=1,2,…,m)。
(20)
将cubature采样点Xi,k-1|k-1通过非线性航姿系统动力学方程进行传递预测。

(21)
计算航姿状态预测值和状态协方差预测值。
(22)
step 3 航姿滤波状态修正。

(23)
计算cubature采样点Xi,k|k-1(i=1,2,…,m)。

(24)
将cubature采样点Zi,k|k-1通过非线性航姿观测方程进行更新修正。
Zi,k|k-1=h(Xi,k|k-1)
(25)

(26)
计算航姿滤波增益矩阵Kk。
(27)
计算航姿状态更新值和状态协方差更新值。
(28)

图1 非线性航姿滤波框图
3 动态自适应调节因子
无人机在不同的飞行条件下,加速度计的三轴加速度会发生很大变化,特别是某些有害的加速度或异常测量值可能会对加速度数值产生影响。此外,在无人机飞行期间,机体抖动和气流扰动也会使加速度数值具有不确定性。因此本文在自适应调节传感器噪声方差的基础上,设计了一种动态自适应调节因子来改善加速度计观测噪声方差,并且将无人机的飞行条件分为静态条件、低动态条件和高动态条件。图2是动态自适应SVDCKF滤波框图,其中动态加速度因子可以由(29)式定义。

(29)
式中,[afx,afy,afz]T是加速度计在机体系的三轴加速度,g是当地重力加速度。

图2 动态自适应SVDCKF滤波框图
3.1 静态条件
无人机起飞之前,在水平地面的飞行状态可以假定为静态条件。此时三轴加速度仅受当地重力加速度和机体轻微抖动的影响。由于本文使用低成本惯性器件,器件本身带有很大的传感器噪声。

(30)
(31)

3.2 低动态条件
无人机在飞行过程中,受到机体抖动和气流扰动的影响,传递到加速度计中产生有害加速度,这些有害加速度会污染三轴加速度数值,进而导致无人机姿态解算失败。

(32)
如果动态加速度因子∂满足(32)式,那么无人机加速度处于低动态条件,阈值Ta通过实验测试进行设定。加速度噪声方差可以通过(33)式进行调节。
(33)
3.3 高动态条件
无人机在飞行过程中可能会受到一些糟糕的因素干扰,例如强风、乱流以及鸟类。这些突然且急剧的变化都会造成三轴加速度无法使用。
∂>Ta
(34)
如果动态加速度因子满足(34)式,那么无人机加速度处于高动态条件,此时加速度测量噪声需要设置成较大的数值,这样可以消除一些异常的加速度对无人机姿态解算的影响。
(35)
4 仿真和实验结果分析
4.1 实验平台
本文使用图3的实验平台采集无人机航姿传感器数据。其中航姿传感器包括MPU6500惯性测量单元以及HMC5893磁力计。实验过程中,使用图3a)旋翼无人机采集静态条件和低动态条件的航姿传感器数据,使用图3b)固定翼无人机采集高动态条件的航姿传感器数据。

图3 无人机航姿实验平台
4.2 实验结果分析
为了更好地验证所提出的航姿滤波算法的性能,利用采集到的航姿传感器数据,在仿真软件上对算法进行分析,并且与EKF和CKF航姿滤波进行对比。
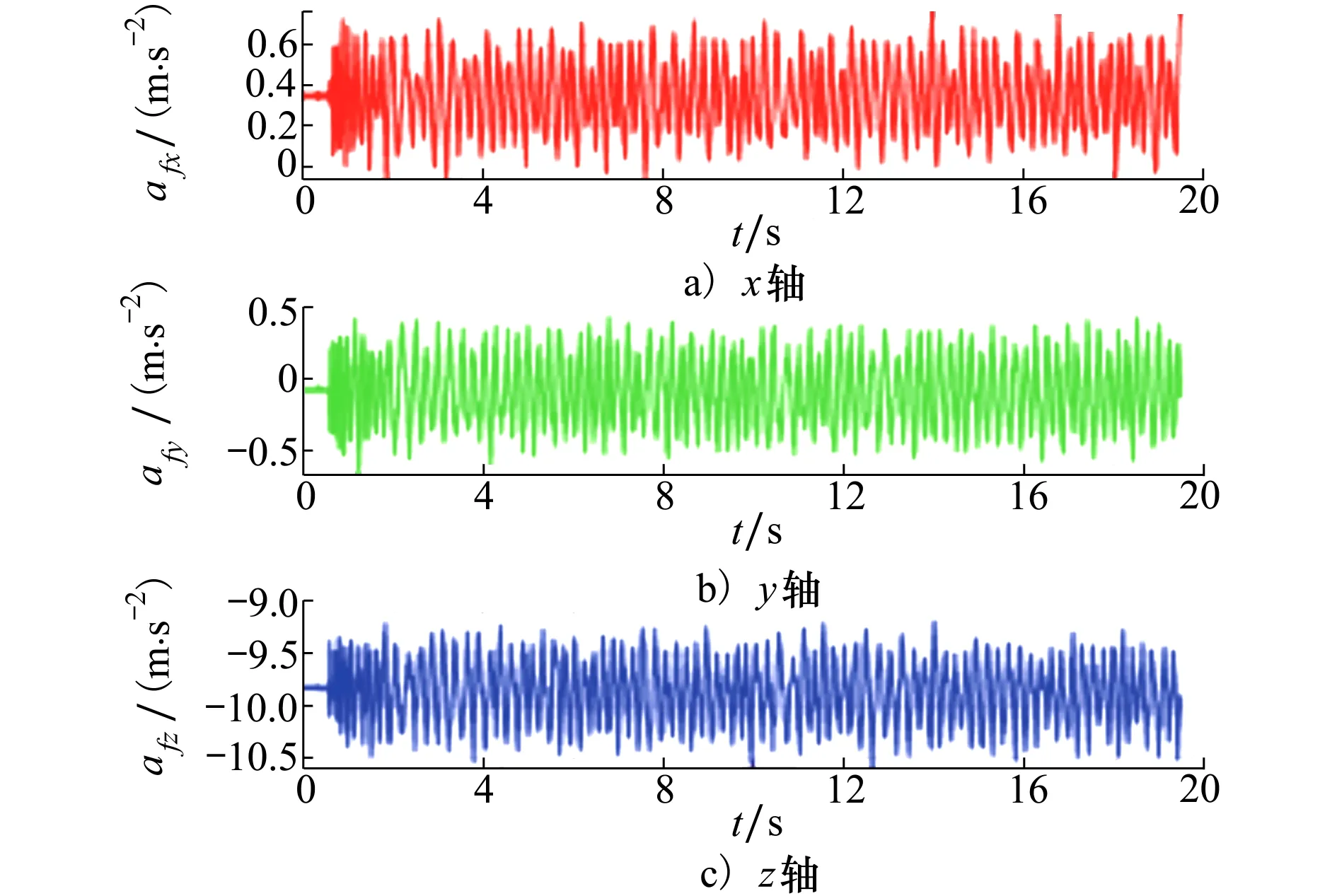
图4 静态条件下的三轴加速度数值变化图
·静态条件
图4描述了无人机在静态条件下的三轴加速度变化,其中X轴的变化范围为[-0.05,0.6]m/s2,Y轴的变化范围为[-0.55,0.5]m/s2,Z轴的变化范围为[-10.5,-9.5]m/s2。从图5至图7可以看出,相比于EKF和CKF,所提出的航姿滤波算法的姿态误差最小。由于静态条件下三轴加速度变化比较稳定,因此测量噪声对航姿精度的影响较小。此时精确的非线性航姿模型和高维的非线性航姿滤波算法将影响航姿精度的解算。本文设计了一种13维航姿估计的模型和高维奇异值容积卡尔曼滤波,提高了航姿滤波精度,同时减少了一些不确定因素的干扰。
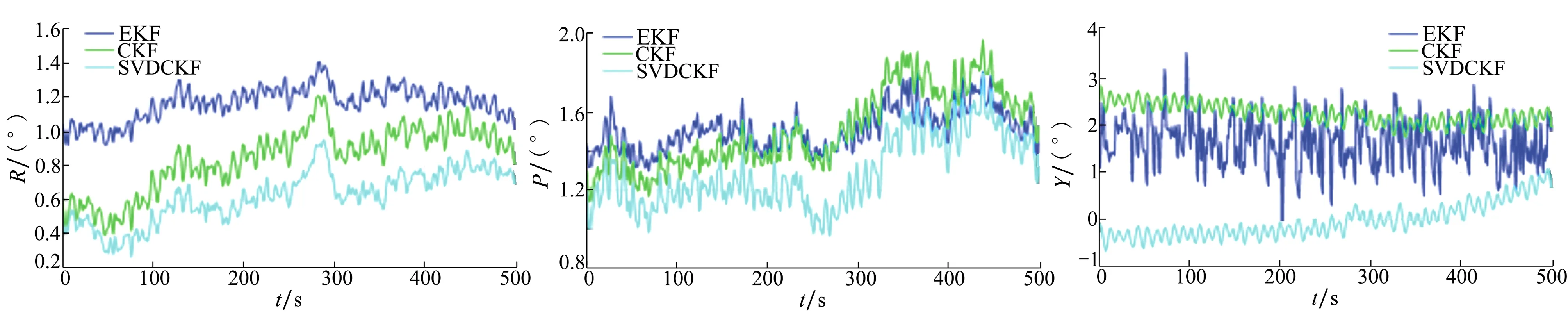
图5 静态条件下的滚转角误差图 图6 静态条件下的俯仰角误差图 图7 静态条件下的偏航角误差图
为了更加直观地比较3种滤波算法的航姿解算精度,表1提供了无人机静态条件下EKF、CKF和SVDCKF航姿精度的平均绝对误差(mean absolute errors,MAE)、标准偏差(standard deviation,STD)以及均方根误差(root mean square errors,RMSE)。从表1中可以看出,对于低成本航姿传感器姿态解算精度而言,本文所提出的算法在航姿解算精度方面优于EKF和CKF,可以更好地处理无人机非线性航姿模型。

表1 EKF、CKF以及SVDCKF航姿精度对比
·低动态条件
图8描述了无人机在低动态条件下的三轴加速度变化,其中X轴的变化范围为[-2,4]m/s2,Y轴的变化范围为[-2,2]m/s2,Z轴的变化范围为[-10.5,-8.5]m/s2。

图8 低动态条件下的三轴加速度数值变化图
从图9至图11中可以看出,在低动态条件下,EKF航姿滤波姿态误差最大,主要是因为EKF对非线性航姿模型的一阶截断描述引入了舍入误差,进而传递到航姿解算,放大了航姿解算的误差。虽然CKF航姿解算误差要小于EKF,但是在低动态飞行过程中,三轴加速度测量值会受到一些不确定因素的干扰,此时加速度量测噪声将会不断变化。CKF由于设置的是恒定的加速度量测噪声方差,无法消除这些干扰带来的影响。因此本文设计了动态自适应调节因子∂,通过∂来不断地调节加速度噪声方差,减少了航姿误差。
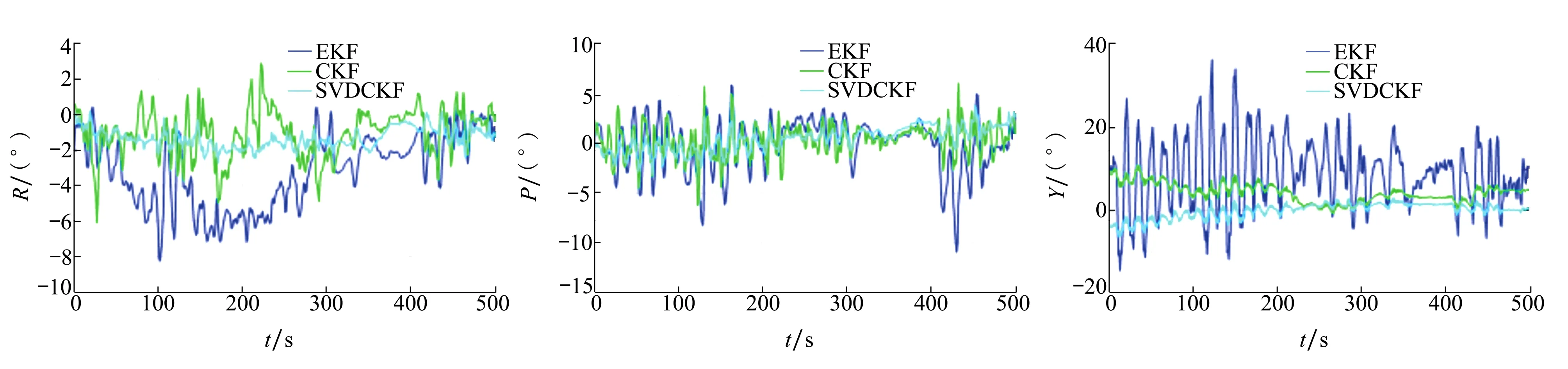
图9 低动态条件下的滚转角误差图 图10 低动态条件下的俯仰角误差图图11 低动态条件下的偏航角误差图
表2提供了无人机低动态条件下EKF、CKF和SVDCKF航姿精度的平均绝对误差、标准偏差以及均方根误差。从表2中可以看出,带有动态自适应调节因子的SVDCKF航姿滤波算法精度要优于EKF和CKF,提高了算法的鲁棒性和抗扰性。

表2 EKF、CKF以及SVDCKF航姿精度对比
·高动态条件
图12描述了无人机在高动态条件下的三轴加速度变化,其中X轴的变化范围为[-10,10]m/s2,Y轴的变化范围为[-6,1]m/s2,Z轴的变化范围为[-10.5,-4.5]m/s2。本文使用固定翼无人机采集高动态飞行条件下的航姿传感器数据。与旋翼无人机相比,固定翼无人机飞行速度快、机动灵活。从图13至图15中可以看出,EKF航姿滤波的姿态误差在40 s后急剧变化,这是因为高动态条件下,航姿模型的非线性程度增强,引起EKF一阶截断带来的舍入误差越来越大。在高动态条件下,带有动态自适应调节因子的SVDCKF相比于CKF,对加速度量测噪声的处理效果更好,消除了非加速度对航姿解算的影响,提高了解算精度。
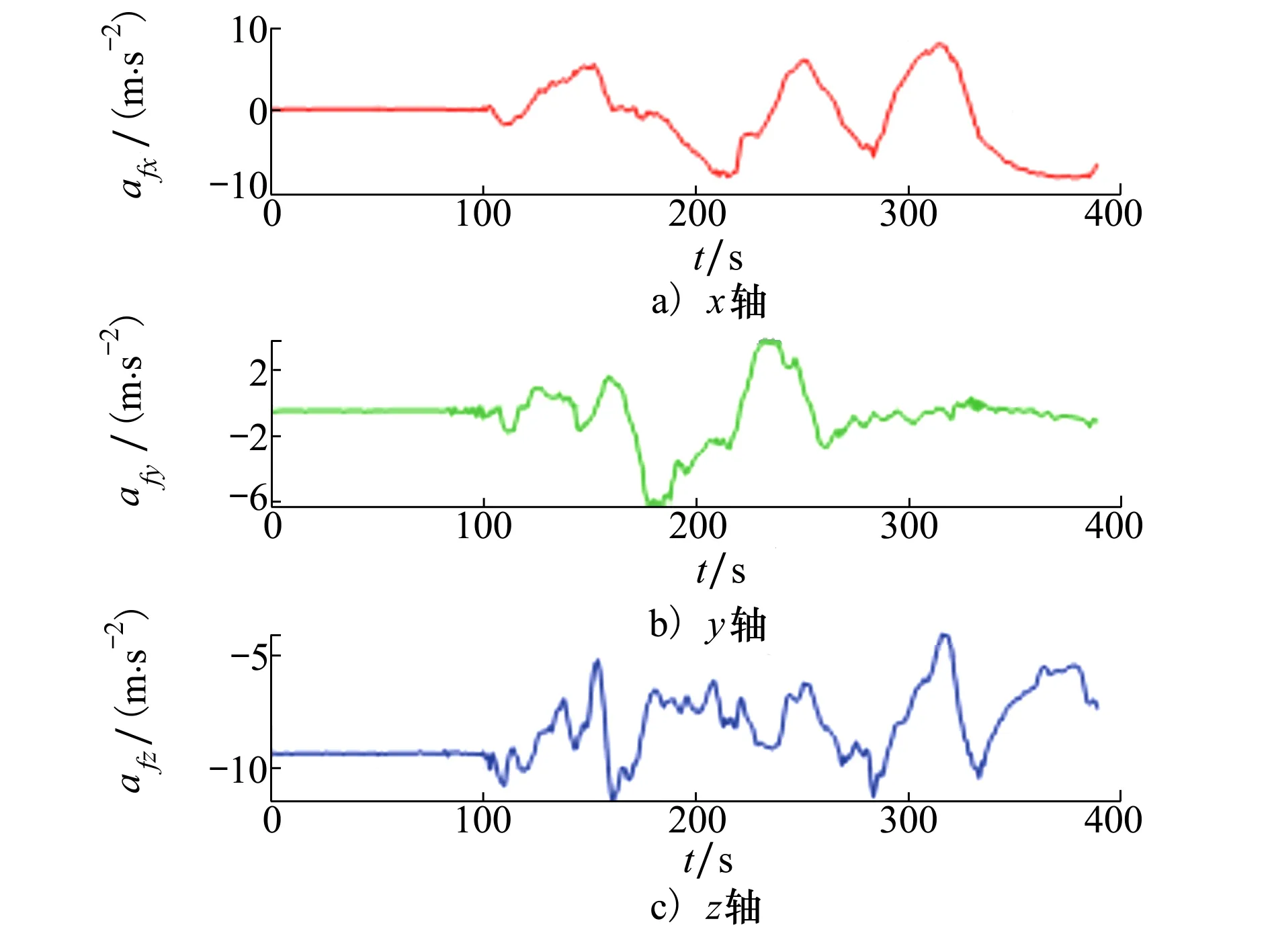
图12 高动态条件下的三轴加速度数值变化图

图13 高动态条件下的滚转角误差图 图14 高动态条件下的俯仰角误差图图15 高动态条件下的偏航角误差图
表3提供了无人机高动态条件下EKF、CKF和SVDCKF航姿精度的平均绝对误差、标准偏差以及均方根误差。从表3中可以看出,本文所提出的航姿滤波算法在高动态条件下通过调节动态自适应因子,降低了航姿解算误差,提高了航姿解算的鲁棒性。

表3 EKF、CKF以及SVDCKF航姿精度对比
5 结 论
本文提出了一种带有动态自适应调节因子的SVDCKF非线性航姿滤波算法,以小型无人机为研究对象,对无人机飞行时的航姿解算需求进行了分析和设计,提高了无人机航姿解算精度和鲁棒性。相比于其他航姿算法,本文提出的航姿算法主要有以下优点:
1) 设计了一种航姿状态的非线性航姿系统模型,将陀螺仪、加速度计以及磁力计随机偏差作为状态估计参数,消除了航姿传感器随机误差对航姿解算精度的影响。
2) 针对无人机航姿模型的非线性问题,以及在滤波过程中状态协方差出现的矩阵非正定问题,用奇异值分解代替Cholesky分解,然后与容积卡尔曼滤波结合,对非线性航姿模型进行处理,提高了航姿解算精度。
3) 对于无人机在复杂条件飞行时,三轴加速度的变化对航姿解算的影响,设计了一种动态自适应调节因子对加速度量测噪声方差进行处理,提高了航姿滤波的鲁棒性和抗扰性。

