边棱音管乐器发音机理与音效的分析

张婷玉，姜 晶，杨 虹

（北京信息科技大学，北京 100101）

弦乐器、管乐器和打击类乐器是常见的三种乐器，其中，管乐器占有重要的地位。一般而言，管乐器发出的乐音是由管内空气柱做周期性的振动形成驻波而产生的。实际上，管乐器的音效会受多重因素的影响，需要对此进行深入探索。

管乐器的发展历史悠久，种类繁多，宋元时期便有了双凤管、双管、七星管、骆驼管[1-2]等。根据声学性质，一般可以将管乐器划分为开管乐器和闭管乐器两大类。常见的管乐器中，如竹笛、大管的管子等，都属于开管乐器，而单簧管、巴乌等属于闭管乐器。不同的管乐器，其演奏效果有很大差别，比如笛子的音色清脆、明亮，演奏技巧很丰富，表现力强，可以演奏不同风格的乐曲，而箫的音色则是圆润、柔和的[3-4]，适合吹奏悠长、抒情的乐曲。

即便对于同一种管乐器，由于演奏技巧的差异，也会产生不同的音效，由此也就展示了不同流派（吹奏大师）在音乐表现上的独特魅力。这些独特的技巧包含对气流高超的掌控能力，这就是艺术。了解管乐器的发音机理，并研究音效与气流流速、吹角、吹口位置等多重因素之间的复杂关系，便是悟理。从术到理，可以更好地指导演奏者吹奏乐器，提升演奏表现能力。

本文从设计边棱音管到拾取音频信号，并对音频信号进行分析处理，结合CFD模拟对气流流速与音效之间的关系进行深入探索。

1 边棱音管乐器的发音机理

边棱音管乐器的发音，是由管口处气源形成的稳定气流，撞击管口边缘产生边棱音，同时激发管中空气柱做周期性振动，并耦合放大后产生的[5-6]。具体原理为：当吹口喷出连续、稳定的气流，以一定角度射向对侧的管边棱时，气流沿着边棱的上下两面逐渐扩张，与原来静止的气流混合，并一同产生旋转波动，当振动着的气流被边棱中分时，便会形成两股上下分离的气体涡旋[7]，由于气流受到阻碍，改变了其各个质点的流速，并且产生了压强差, 流速小的压强大，流速大的压强小，压强大的质点就会向压强小的质点方向移动[8-9]。因此，在气压的作用下，涡旋之间产生空吸现象，涡旋之间相互吸引碰撞，在气流连续不断地产生时，涡旋也将持续碰撞发出声音，即产生边棱音[10-16]。

边棱音本身是非常微弱的，需要通过与边棱音管的振动耦合放大，才能发出声音，其耦合过程为：边棱音刚产生时，频率非常高，在激发边棱音管中的空气柱振动后，空气柱又反作用于边棱音，将其频率拉低到空气柱的固有频率附近，当边棱音与空气柱的固有频率很接近时，便会发出稳定的声音，此声音信号频率与空气柱的理论频率有些许差异。而在管口处脱离的涡旋，由于内部不稳定性与流体粘性的作用，在向下运动过程中，不断撞击管的腔体后侧，产生扰动，向管内的声场传递能量[17]，同时，该扰动又反馈回腔体前缘，影响之后涡旋的形成，形成一个具有谐振特性的能量反馈回路[18-19]（图1）。

图1 气流驱动空腔振荡能量反馈回路

本文选取流速这一因素，分别从实验和模拟仿真的角度，探究流速变化对边棱音频率的影响，以及耦合之后对边棱音管乐器发音效果的影响。

2 边棱音数值模拟

2.1 几何模型和变量控制

本文应用CFD软件，基于有限体积法（Finite volume method, FVM）求解器，对边棱音管乐器管口边棱在吹嘴发出的不同流速的射流作用下的流场进行数值计算，从而辅助说明边棱音管的谐振频率随吹速变化的现象。由于边棱音是短促、微弱、不稳定的效应，达到稳定状态后，将与管内空气柱的谐振耦合。为了研究边棱音的振动频率，需要去掉谐振腔部分进行变量控制，建立的吹嘴与管口边棱二维几何模型如图2所示。吹嘴出口到直角边棱的距离l为20 mm，吹嘴直径d为3 mm，吹嘴中心点与边棱尖端处于同一条水平线上。本文数值计算中，保持l不变，通过改变吹速v，研究涡流形态及边棱音频率的变化。流体设置为25 ℃空气，密度为ρ= 1.185 kg/m3，动态黏度系数为μ= 1.831×10-5kg/ms。流体的雷诺数（Reynolds numbers）Re= ρvd/μ，本文中假设流体的流动形态为层流，且不可压缩。

2.2 数值计算结果与讨论: 吹嘴流速对边缘音的影响

由图2可知，吹嘴发出的射流抖动并在边棱处发生涡旋脱落，形成一系列交替分布的涡街。图2所示边棱上方监测点处，在不同吹速下的声压信号如图3（a）（c）（e）所示，对声压信号的稳态响应经快速傅里叶变换（FFT）计算得到频谱如图3（b）（d）（f）所示。由图3可知，不同吹速下的声压信号是由多个频率的信号叠加形成的复杂波形。把不同频率区间的信号称为频率阶段，以下对频率阶段的出现及其原因进行讨论。

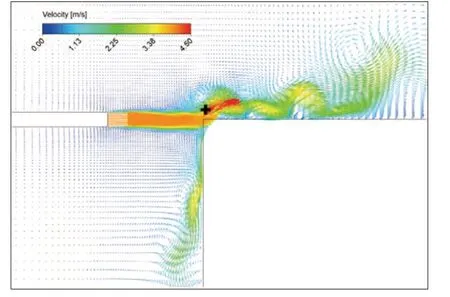
图2 管口边棱气流速度矢量图

边棱音的振动频率取决于两个主要因素，吹速v和吹嘴与边棱的距离l。若连续改变吹速v，边棱音的频率将连续发生变化。在一定范围内，边棱音频率将出现突然跳变到另一个频率阶段的现象。频率阶段的出现是由于喷嘴出射的射流和边棱需要保持特定相位关系，在一定范围内，频率的连续小幅度变化不足以满足该相位关系，从而产生频率的跳变[20]。当边棱音频率发生阶跃时，涡流形态也发生变化。基于图3所示的频谱，提取出频率峰值。如图4所示，当射流流速较低时，频谱中只有一个频率峰值，此时为边棱音的第一阶段。当吹速增大到1.25 m/s时，边棱音频率由29 Hz跳变为60 Hz，频谱中出现两个频率峰值，此时为边棱音的第二阶段。由图4可知，当边棱音频率由第一阶段向第二阶段跳变时，第一阶段并未消失，新的第二阶段与第一阶段共存。继续增大吹速，吹速增加为4 m/s时，频率跳变为318 Hz，出现边棱音的第三个阶段，此时，边棱音三个阶段共存。如图4所示，在各个频率阶段，边棱音的振动频率f随着吹速v的增加而提高。

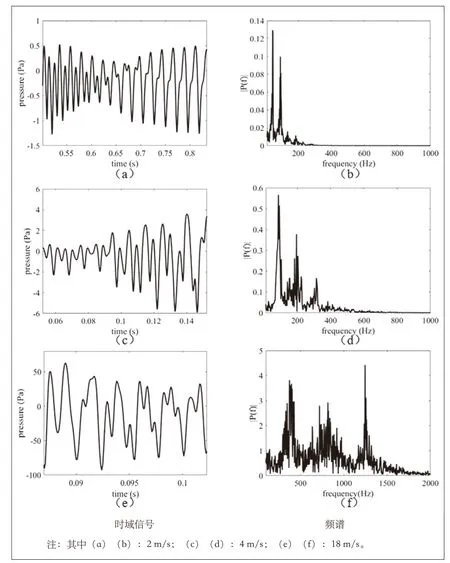
图3 不同吹速的声压信号

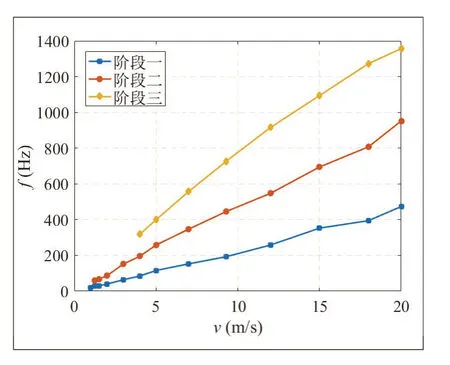
图4 边棱音频率与吹速关系

以上通过数值模拟，展示了吹嘴发出的射流在管口边棱处发生涡旋脱落产生边棱音，以及边棱音频率随着射流流速增加出现的阶跃现象。在每个频率阶段，边棱音的振动频率随着吹速的增加而增加。由于边棱音通常微弱而短促，边棱处的边棱音将与边棱音管内空气柱的谐振耦合，其振动频率与边棱音管的固有频率互相影响。以下通过实验，研究边棱音与边棱音管乐器空气柱谐振之间的耦合现象。

3 实验探究边棱音管乐器的音效

3.1 边棱音管发音拾音装置

本文设计了一套实验装置，实现边棱音管的发音、拾音与音效分析。实验时，采用气泵驱动边棱音管发出稳定的声音信号，用G.R.A.S. 40PP CCP Free-field QC Microphone振动传感器拾取音频信号，用LabVIEW编写音频信号测试系统，结合MATLAB软件，对音频信号进行分析处理。

音频信号测试系统界面如图5所示，可采集声音信号，提取声音信号的频率、幅值，并对音高进行标定，以音分为单位进行偏离校对。系统也可以直观地显示基频、倍频等物理量。

实验条件：边棱音管内管径D内=44.1 mm，外管径D外=50.3 mm，管长L=800.0 mm，温度为24℃，湿度为30%。

3.2 不同流速对音效影响的探究

实验获得的不同流速条件下的边棱音管声谱图，如图6所示。在0 s～8 s时段，气体流速U1为19.8 m/s，流速较低，在管口边棱处形成稳定气流，此时边棱音的频率到达管内空气柱基频附近。经过耦合，边棱音管的主导频率便为[206.5，208.0] Hz的基频，但幅值较小，此时的二次谐波和三次谐波虽然也存在，但其幅值远小于基频；随着射流速度的进一步增大，8 s～16 s时段，气体流速U2增至59.5 m/s，边棱音频率也不断向高频发展，并且产生阶跃现象，此时边棱音频率增加到空气柱的二倍频附近。故经耦合后的边棱音管的主导频率便突增到二倍频，为[413.0，416.0] Hz，且幅值最大，同时二次谐波与一次谐波共存（见图6区域Ⅰ），基频幅值逐渐减弱；继续增大流速，16 s～20 s时段，流速U3增为79.4 m/s，边棱音的频率又经历了一次阶跃，到达空气柱三倍频的区域附近，此时耦合后的管频增大到三倍频，为[618.5，624.0] Hz，并且边棱音管的各次谐波同时存在（见图6区域Ⅱ）。

图5 音频信号测试界面

图6 不同流速下的边棱音管声谱图

由仿真模拟部分可知，边棱音的振动频率随着吹速的增加而增加，并且在一定范围内，边棱音的频率阶段会随着流速的增加而跳变到更高的阶段。由于边棱音管的频率是经过边棱音与空气柱耦合之后所得，因此，边棱音管频率的变化应由以上两种变化的综合效应影响所得。

4 结语

边棱音管乐器的发音是由气流撞击管壁产生边棱音，进而和管体振动耦合形成的。实验和模拟仿真均表明，气流的流速大小会影响边棱音管的音效，包括音量、音调和音色等。气体的流速越大，边棱音的振动越充分，振幅也随之变大，音量也就越大。气体流速变化会产生音频信号频率阶段跳变的现象，流速越大，频率越高。在管乐器的演奏中，有一种“超吹”的技巧，即管的基频被抑制，某一泛音被突出的现象，便是这一结论的充分体现。可见，气体流速对管乐器发音的影响是至关重要的。

影响管乐器音效的因素还包括吹角、吹口位置、管材及形制等，多种因素共同影响管乐器的发音。本文采用实验与模拟手段相结合，可为下一步研究和应用提供方向性指导，从而得出一套多重因素对管乐器音效影响的更系统科学的结论。