薄平板断面气动自激力振幅效应数值模拟

刘志文　张瑞林　陈政清

摘   要：为研究振幅对桥梁主梁断面气动自激力的影响，以薄平板断面为研究对象，采用计算流体动力学（Computational Fluid Dynamics，CFD）方法进行氣动自激力振幅效应研究. 首先采用强迫振动数值模拟方法，研究了不同振幅下薄平板断面颤振导数与气动力迟滞相位，分析了薄平板断面气动力的频谱特性;然后采用自由振动数值模拟方法，研究了薄平板断面的颤振响应演变规律.薄平板断面强迫振动数值模拟结果表明：扭转振幅对薄平板断面颤振导数影响较大，在高折算风速下，颤振导数A*

2随着振幅的增大由负转正，竖向振幅对薄平板断面颤振导数影响相对较小;扭转振幅的增大引起薄平板断面气动力迟滞相位正弦值发生了较大变化;当扭转振幅大于8°时，薄平板断面气动力存在较为明显的高次谐波分量，主要为三阶与五阶分量，竖向振幅引起的薄平板断面气动力高阶分量不明显.薄平板断面自由振动数值模拟结果表明：薄平板断面在颤振发散过程中，其瞬时频率、瞬时阻尼比与竖向扭转位移相位差均随振幅变化.

关键词：薄平板断面;气动自激力;振幅;颤振;数值模拟

中图分类号：U441.3                               文献标志码：A

Numerical Simulation of Amplitude Effects on

Aerodynamic Self-excited Forces of Thin Plate Section

LIU Zhiwen1，2?，ZHANG Ruilin1，CHEN Zhengqing1，2

（1. Hunan Provincial Key Laboratory for Wind and Bridge Engineering （Hunan University），Changsha 410082，China;

2. College of Civil Engineering，Hunan University，Changsha 410082，China）

Abstract： In order to study the amplitude effects on self-excited aerodynamic forces of the bridge main deck section，a thin plate section was taken as the research object，and the amplitude effects of aerodynamic self-excited forces were studied by using computational fluid dynamics（CFD） method. First，the numerical simulation method of forced vibration was used to investigate the flutter derivatives and aerodynamic hysteresis phases of the thin plate section under different amplitudes. The aerodynamic spectrum characteristics of the thin plate section were analyzed. Then，the numerical simulation method of free vibration was used to study the flutter response evolution characteristics of the thin plate section. The numerical simulation results of forced vibration for the thin plate section show that the torsional amplitude has significant effects on the flutter derivatives of the thin plate section. At high reduced wind speed，the flutter derivative A*

2 changes from negative to positive as the amplitude increases. The effect of vertical amplitude on the flutter derivatives of the thin plate section is relatively small. As the torsional amplitude increases，the sinusoidal value of aerodynamic hysteresis phase of the thin plate section changes significantly. When the torsional amplitude is larger than eight degrees，there are obvious high-order harmonic components in the aerodynamic forces of the thin plate section，mainly for the third and fifth order components. The high-order components of aerodynamic forces of the thin plate section caused by the vertical amplitude are not obvious. The numerical simulation results of the free vibration of the thin plate section show that the instantaneous frequency，damping ratio and the phase difference between the vertical displacement and torsional displacement change with the vibration amplitude during the process of flutter divergence.

Key words：thin plate section;self-excited aerodynamic forces;amplitude;flutter;numerical simulation

1940年，舊塔科马桥在19 m/s左右的风速下发生大幅振动，扭转振幅大约为35°，并在长时间振动下因吊杆断裂导致垮塌[1]. 此后，桥梁结构气动稳定性问题受到广泛关注，Scanlan等[2]将航空领域的颤振导数概念加以推广，建立了适用于桥梁主梁断面的线性颤振理论，为现代大跨度桥梁抗风设计提供指导.随着桥梁跨度的进一步增加，大跨桥梁主梁在强风作用下可能会出现大幅振动现象，传统的Scanlan线性颤振理论难以适用于桥梁主梁大幅振动情况. 国内外许多学者开始关注振幅对桥梁主梁断面的颤振性能影响.

桥梁主梁断面气动力在大振幅条件下存在高次谐波分量. 陈政清等[3]通过强迫振动风洞试验研究发现钝体桥梁主梁断面存在明显的高次谐波分量. Diana等[4-5]通过墨西拿海峡大桥主梁断面风洞试验研究，发现气动力存在高次谐波分量和气动力的迟滞效应. 王骑[6]通过风洞试验研究发现大振幅下薄翼断面与流线型箱梁断面气动力存在显著的高次谐波

分量. 唐煜[7]采用计算流体动力学方法（Computational Fluid Dynamics，CFD）进行了薄平板断面与流线型箱梁断面强迫振动研究，结果表明：大振幅下气动力存在高次谐波分量，并且振幅越大，高次谐波分量越明显. 熊龙等[8]、Lin等[9]分别进行了流线型箱梁断面与B/H=5矩形断面（B、H分别为矩形断面的宽度与高度）强迫振动风洞试验研究，结果表明：较大扭转振幅下流线型箱梁断面与B/H=5矩形断面气动力存在显著的高次谐波分量. Gao等[10]、Zhang等[11]分别在双边肋主梁断面与流线型箱梁断面极限环颤振中发现气动力存在二阶与三阶分量.

颤振导数是表征桥梁结构断面气动力的主要参数，为此部分学者进行了典型断面颤振导数的振幅效应研究. Noda等[12]通过风洞试验研究了宽高比B/H=13与150的薄矩形断面在不同振幅下的颤振导数，研究表明：扭转振幅对薄矩形断面颤振导数A*

2影响较大. 熊龙等[8]、Lin等[9]分别进行了流线型箱梁断面与B/H=5矩形断面大振幅的强迫振动风洞试验研究，结果表明：扭转振幅对流线型箱梁断面与B/H=5矩形断面颤振导数影响较大，其中对A*

2的影响最为明显. Zhang等[11]采用CFD的方法进行了流线型箱梁断面的强迫振动研究，结果表明：箱梁断面颤振导数具有显著的振幅相关性，而对竖向扭转模态耦合因素不敏感.

综上所述，国内外许多学者开展了主梁断面气动力的振幅效应的试验与数值模拟研究，已有研究表明：大振幅下气动力存在高阶分量，而且随振幅的增大颤振导数会发生改变. 但目前对桥梁断面气动力幅值与迟滞相位随振幅变化以及非线性气动力作用下颤振位移响应演变规律的研究较少.

为此，本文选取薄平板断面作为研究对象[3，7，13]，采用CFD方法进行薄平板断面气动自激力的振幅效应研究. 首先采用强迫振动数值模拟方法，比较了不同振幅下的薄平板断面颤振导数与气动力迟滞相位，分析了薄平板断面气动力的频谱特性，然后采用自由振动数值模拟方法，分析了薄平板断面的颤振响应演变规律. 此外，为验证本文CFD数值模拟结果的可靠性，将颤振导数与颤振临界风速结果与理想平板理论解以及已有文献试验结果进行了对比.

1   数值计算方法

1.1   流体力学控制方程

目前，在桥梁结构风工程领域，基于雷诺平均法（RANS）的数值模拟方法被广泛采用[14-15]，其原理是将瞬态方程中的场变量分解为时均值和脉动值：

? = [?] + ?′       （1）

式中：?为通用变量，可以代表速度、压力等求解变量;[?]与?′分别为场变量在某时间步内的平均值和脉动值. 对于二维不可压缩流体，其控制方程为：

= 0       （2）

+=-+μ-    （3）

式中：[u]i为某时间步内的速度分量平均值;xj为笛卡尔坐标;[p]为某时间步内的压力平均值;ρ为空气密度，ρ = 1.225 kg/m3;μ为动力粘性系数，在标准大气压、温度为20 ℃条件下取μ = 1.789 4×10-5 kg/（m·s）.

1.2   求解与计算

本文采用大型商业软件ANSYS Fluent求解流场，采用剪应力输运湍流模型（SST k-w）以使流体控制方程封闭，基于有限体积法求解控制方程.空间离散采用二阶迎风格式，时间离散采用二阶隐式时间积分. 基于SIMPLEC算法处理压力-速度耦合.

数值模拟计算在DELL Precision 7920 Tower工作站进行，采用4个核并行计算，网格数量约为8.57万，计算效率约为1 h/千步.

1.3   强迫振动与自由振动数值模拟方法

采用大型流体力学分析软件ANSYS Fluent动网格技术，通过动网格驱动宏（DEFINE-CG-MOTION）实现结构断面运动. 对于结构强迫振动，指定结构断面相应速度即可实现结构运动状态更新. 对于结构自由振动，通过求解结构振动方程得到结构振动的位移响应，再通过动网格实现结构运动状态的更新. 结构在升力和升力矩作用下的振动方程为：

m（[h] + 2ξh0 wh0 [h]+ w2

h0h） = Lse    （4）

I（[a] + 2ξa0 wa0[a] + w2

a0a） = Mse    （5）

式中：m为单位长度质量;ξh0为竖向运动阻尼比;wh0为竖向运动圆频率;I为单位长度惯性矩;ξa0为扭转运动阻尼比;wa0为扭转运动圆频率;Lse、Mse分别为升力与升力矩. 结合Fluent动网格技术，通过用户定义函数（UDF）将Newmark-β数值算法嵌入Fluent中以求解式（4）（5），计算薄平板断面自由振动响应.

1.4   薄平板断面及计算域

薄平板断面宽度B为0.45 m，高度H为0.001 m，宽高比B/H为450 ∶ 1. 计算域设为40B×20B（B为薄平板断面宽度）. 图1所示为薄平板断面形状以及计算域与边界条件. 计算域与边界条件如下：计算域左侧为速度入口边界（Velocity inlet），计算域右侧为压力出口边界（Pressure outlet），计算域上下侧为对称边界（Symmetry），薄平板断面为固定壁面边界（Wall）.

1.5   網格无关性与时间步无关性验证

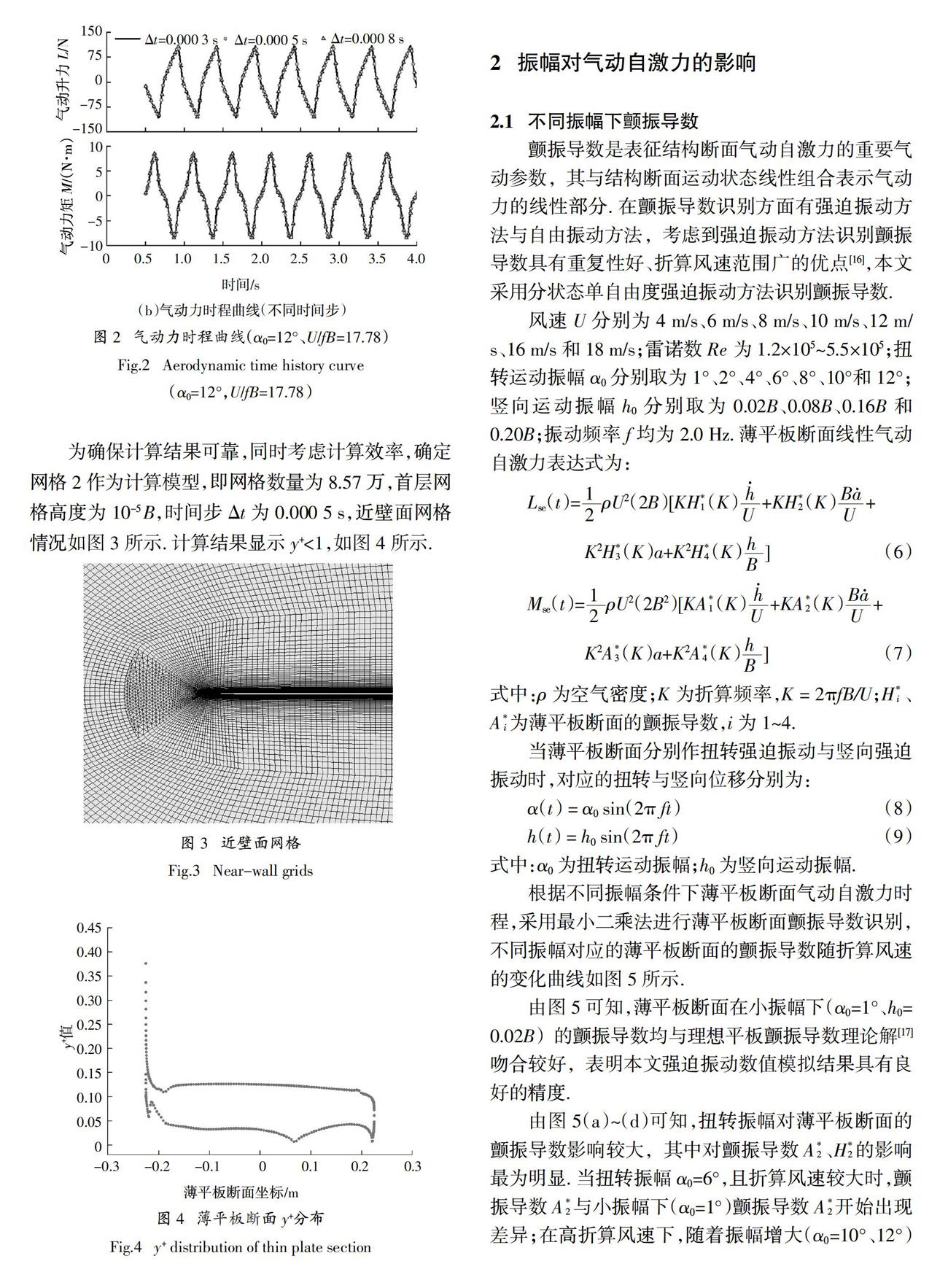
以扭转振幅α0 = 12°、折算风速U/fB = 17.78的强迫振动为例进行网格无关性与时间步无关性验证. 不同网格划分方案如表1所示，图2（a）所示为气动升力与力矩时程计算结果，其中时间步Δt均为0.000 5 s. 由图2（a）可知不同网格方案计算得到的气动升力与力矩时程曲线几乎完全一致. 对网格2进行时间步无关性验证，时间步Δt分别为0.000 3 s、0.000 5 s与0.000 8 s，图2（b）所示为气动升力与力矩时程计算结果，由图2（b）可知不同时间步计算得到的气动升力与力矩时程曲线几乎完全一致.

为确保计算结果可靠，同时考虑计算效率，确定网格2作为计算模型，即网格数量为8.57万，首层网格高度为10-5 B，时间步Δt为0.000 5 s，近壁面网格情况如图3所示. 计算结果显示y+<1，如图4所示.

2   振幅对气动自激力的影响

2.1   不同振幅下颤振导数

颤振导数是表征结构断面气动自激力的重要气动参数，其与结构断面运动状态线性组合表示气动力的线性部分. 在颤振导数识别方面有强迫振动方法与自由振动方法，考虑到强迫振动方法识别颤振导数具有重复性好、折算风速范围广的优点[16]，本文采用分状态单自由度强迫振动方法识别颤振导数.

风速U分别为4 m/s、6 m/s、8 m/s、10 m/s、12 m/s、16 m/s和18 m/s;雷诺数Re为1.2×105～5.5×105;扭转运动振幅α0分别取为1°、2°、4°、6°、8°、10°和12°;竖向运动振幅h0分别取为0.02B、0.08B、0.16B和0.20B;振动频率f均为2.0 Hz. 薄平板断面线性气动自激力表达式为：

式中：ρ为空气密度;K为折算频率，K = 2πfB/U;H*

i、A*

i为薄平板断面的颤振导数，i为1～4.

当薄平板断面分别作扭转强迫振动与竖向强迫振动时，对应的扭转与竖向位移分别为：

α（t） = α0 sin（2π ft）     （8）

h（t） = h0 sin（2π ft）     （9）

式中：α0为扭转运动振幅;h0为竖向运动振幅.

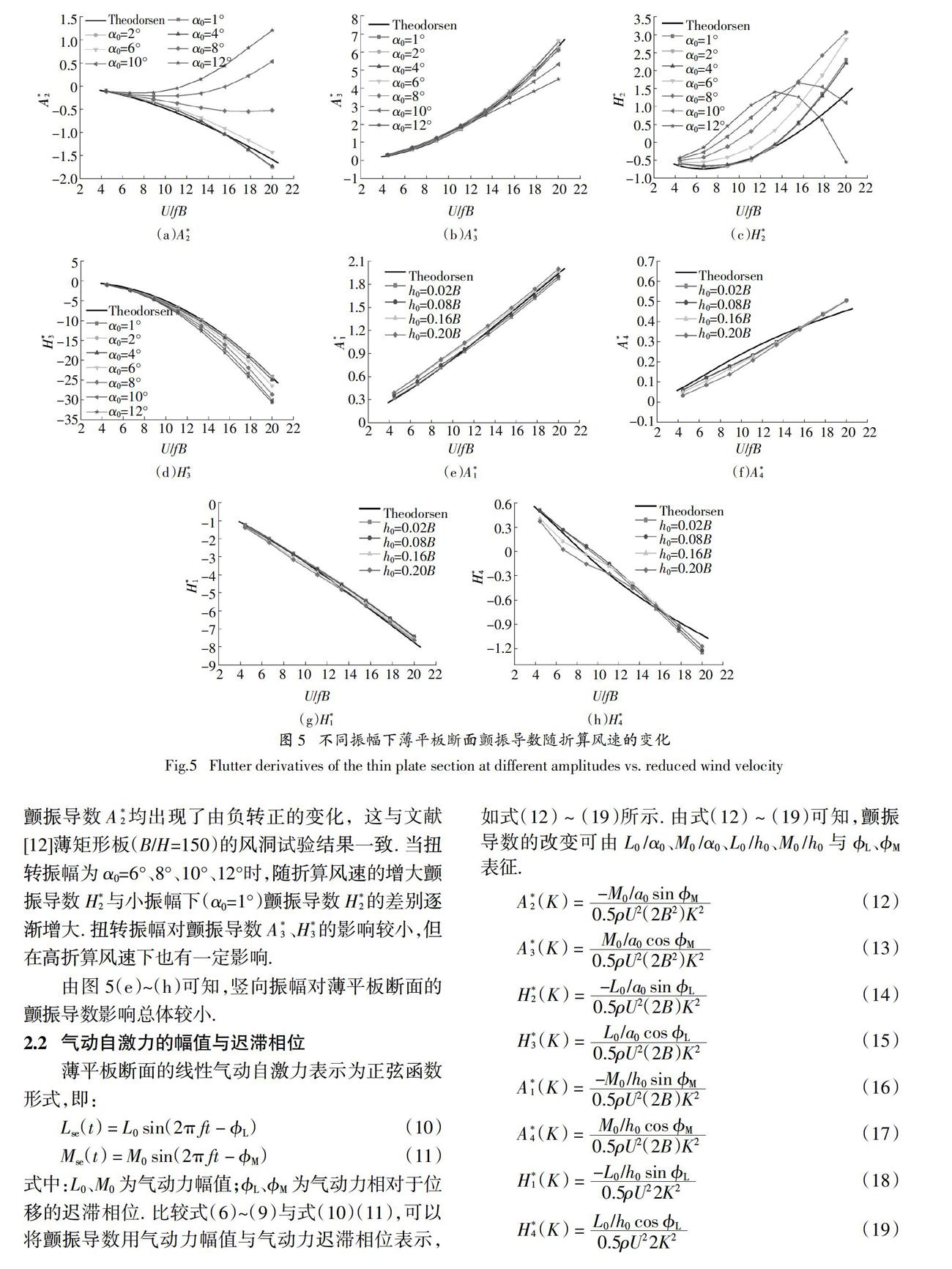
根据不同振幅条件下薄平板断面气动自激力时程，采用最小二乘法进行薄平板断面颤振导数识别，不同振幅对应的薄平板断面的颤振导数随折算风速的变化曲线如图5所示.

由图5可知，薄平板断面在小振幅下（α0=1°、h0=0.02B）的颤振导数均与理想平板颤振导数理论解[17]吻合较好，表明本文强迫振动数值模拟结果具有良好的精度.

由图5（a）～（d）可知，扭转振幅对薄平板断面的颤振导数影响较大，其中对颤振导数A*

2、H*

2的影响最为明显. 当扭转振幅α0=6°，且折算风速较大时，颤振导数A*

2与小振幅下（α0=1°）颤振导数A*

2开始出现差异;在高折算风速下，随着振幅增大（α0=10°、12°）颤振导数A*

2均出现了由负转正的变化，这与文献[12]薄矩形板（B/H=150）的风洞试验结果一致. 当扭转振幅为α0=6°、8°、10°、12°时，随折算风速的增大颤振导数 H*

2与小振幅下（α0=1°）颤振导数H*

2的差别逐渐增大. 扭转振幅对颤振导数A*

3、H*

3的影响较小，但在高折算风速下也有一定影响.

由图5（e）～（h）可知，竖向振幅对薄平板断面的颤振导数影响总体较小.

2.2   气动自激力的幅值与迟滞相位

薄平板断面的线性气动自激力表示为正弦函数形式，即：

Lse（t） = L0 sin（2π ft - ?L）     （10）

Mse（t） = M0 sin（2π ft - ?M）     （11）

式中：L0、M0为气动力幅值;?L、?M为气动力相对于位移的迟滞相位. 比较式（6）～（9）与式（10）（11），可以将颤振导数用气动力幅值与气动力迟滞相位表示，如式（12） ～ （19）所示. 由式（12） ～ （19）可知，颤振导数的改变可由L0 /α0、M0 /α0、L0 /h0、M0 /h0与?L、?M表征.

根据薄平板断面强迫振动模拟所得的气动力，分别对式（10）（11）进行最小二乘拟合，可得到薄平板断面的气动力幅值与迟滞相位，具体结果如图6所示.

由图6（a）～（f）可知，对于扭转运动，L0 /α0、M0 /α0随振幅变化较小. 升力与力矩的迟滞相位的正弦值sin ?Lα、sin ?Μα随振幅变化较大，其中sin ?Mα在折算风速U/fB为20.0时，其值在1°振幅时为0.28，在12°振幅时为-0.26，这也引起了颤振导数A*

2在高折算风速下，随着振幅的增大发生了由负转正的变化. 升力与力矩的迟滞相位余弦值cos ?Lα、cos ?Μα随振幅变化不明显，且其绝对值大多大于0.94，所以迟滞相位并没有引起颤振导数A*

3、H*

3发生较大变化.

由图6（g）～（l）可知，对于竖向运动，L0 /h0、M0 /h0随振幅变化较小. 升力与力矩的迟滞相位的正弦值sin ?Lh、sin ?Μh 变化亦较小，且其绝对值大多大于0.96，所以颤振导数A*

1、H*

1随振幅变化較小. 升力与力矩的迟滞相位的余弦值cos ?Lh、cos ?Μh在低折算风速下略有变化，高折算风速下变化不明显，这引起颤振导数A*

4、H*

4在低折算风速下有较小变化.

2.3   气动自激力频谱特性

采用快速傅里叶变换方法（Fast Fourier Transform，FFT）对薄平板断面单自由度强迫振动得到的气动自激力进行频谱分析，图7为折算风速U/fB为17.78的薄平板断面气动力频谱图.

由图7（a）（b）可知，当薄平板断面的扭转振幅为12°时，升力与力矩均存在明显高阶分量，主要为三阶、五阶等奇数倍频分量;由图7（c）（d）可知，竖向振幅为0.20B时，气动力同样存在高阶分量，主要为三阶分量，与扭转运动相比，竖向运动引起的薄平板断面的气动力高阶分量则相对较小.

为进一步分析扭转振幅对薄平板断面气动力分量的影响，定义气动力分量幅值比Ri：

Ri =  × 100%     （20）

式中：Fi为i阶气动升力或力矩幅值;f为频率;Ff为频率f对应的气动力幅值. 由式（20）计算不同扭转振幅下薄平板断面气动力一阶、三阶与五阶分量的幅值比，结果如图8所示.

由图8可知，随着扭转振幅的增大，薄平板断面气动力一阶分量所占比例不断下降，当扭转振幅大于8°时，薄平板断面气动力出现较为明显的三阶与五阶分量.

3   颤振位移响应演变规律

3.1   颤振临界风速

采用自由振动方法进行薄平板断面颤振稳定性的直接计算[18-19]，薄平板断面自由振动计算特征参数采用文献[1]中的相关参数，如表2所示.

颤振临界状态附近不同计算风速下薄平板断面位移时程曲线如图9所示. 薄平板断面颤振临界风速与频率的计算结果及其与频域理论解如表3所示. 由表3可知，CFD计算误差较小，表明本文自由振动数值模拟结果具有良好的精度.

3.2   颤振位移响应演变规律

非线性气动力作用下，结构振动的频率和阻尼比不是一个常数，而是随振幅变化，可根据薄平板断面自由振位移响应时程计算得到：

ξ（ti） =     （21）

ω（ti） =        （22）

?hα（ti） = ?h（ti） - ?α（ti） = （tαi - thi）wα（ti）   （23）

式中：Q（ti）为第i个位移峰值;ti为第i个位移峰值对应的时间;ξ（t）为瞬时阻尼比;ω（t）瞬时圆频率;?hα（t）为竖向与扭转振动位移相位差. 另外，瞬时阻尼比为系统阻尼与气动阻尼两者共同作用的结果.

图10为薄平板断面在风速U为17.0 m/s（U/fa0B =12.49）时自由振动位移响应时程曲线. 根据位移响应时程由式（21）～（23）计算得到薄平板断面竖向与扭转振动对应的瞬时频率、瞬时阻尼比以及竖向与扭转振动位移相位差随时间变化曲线，如图11所示.

由图11（a）可知，竖向与扭转瞬时频率在小振幅（α0<1.44°）下不随振幅变化，且两者为同一数值. 随着振幅的增大，两者均呈现了减小的趋势，在减小过程中竖向瞬时频率略大于扭转瞬时频率，换言之，是扭转瞬时频率下降略早于竖向瞬时频率. 由于薄平板断面为弯扭耦合颤振，竖向与扭转频率变化趋势具有一致性，但在变化过程中两者频率不是同一个数值. 值得说明的是瞬时频率存在一定跳跃性，这是由时间离散引起的数值误差.

由图11（b）可知，竖向与扭转瞬时阻尼比绝对值随着振幅增大而不断增大，说明颤振发散速率越来越大. 这与颤振导数随振幅变化有关，随着扭转振幅的增大颤振导数A*

2逐渐变小，再变为负值，导致随着扭转振幅的增大颤振导数 提供的气动正阻尼逐渐减小，再变为提供气动负阻尼. 薄平板断面颤振为竖向与扭转耦合的振动形式，所以竖向与扭转瞬时阻尼比的绝对值均随振幅的增大而增大，且竖向与扭转瞬时阻尼比基本保持一致.

由图11（c）可知，扭转振幅α0 > 1.44°时，竖向与扭转位移相位差随着振幅增大不断增大. 竖向位移相位超前于扭转相位，又由于竖向瞬时频率略大于扭转瞬时频率，导致竖向与扭转位移相位差进一步增大.

4   结   论

以薄平板为研究对象，采用计算流体动力学方法进行强迫振动与自由振动研究，分析了气动自激力的振幅效应，得到如下主要结论：

1）扭轉振幅对薄平板断面颤振导数影响较大，其中对A*

2的影响最为明显，在高折算风速下A*

2随着振幅的增大由负转正;竖向振幅对薄平板断面颤振导数影响较小;扭转振幅对气动力迟滞相位正弦值影响较大，而对气动力迟滞相位余弦值影响较小.

2）当扭转振幅大于8°时，薄平板断面气动力存在较为明显高次谐波分量，主要为三阶与五阶分量;竖向振幅引起的薄平板断面气动力高阶分量成分相对较小.

3）薄平板断面颤振发散过程中，竖向与扭转瞬时频率在小振幅（α0 < 1.44°）下基本不随振幅变化，随着振幅进一步增大两者均呈现减小的趋势;竖向与扭转瞬时阻尼比绝对值随着振幅增大而不断增大;扭转振幅α0 > 1.44°时，竖向与扭转位移相位差随着振幅增大不断增大.

参考文献

[1]    项海帆，葛耀君，朱乐东，等. 现代桥梁抗风理论与实践[M]. 北京：人民交通出版社，2005：1—3.

XIANG H F.GE Y J，ZHU L D，et al. Theory and practice of wind resistance of modern bridges [M]. Beijing：China Communications Press，2005：1—3. （In Chinese）

[2]    SCANLAN R H，TOMKO J. Airfoil and bridge deck flutter derivatives[J].  Journal of Engineering Mechanics，ASCE，1971，97 （6）：1717—1737.

[3]    陈政清，于向东. 大跨桥梁颤振自激力的强迫振动法研究 [J].  土木工程学报，2002，35（5）：34—41.

CHEN Z Q，YU X D. A new method for measuring flutter self-excited forces of long-span bridges [J].  China Civil Engineering Journal，2002，35（5）：34—41. （In Chinese）

[4]    DIANA G，RESTA F，ZASSO A，et al. Forced motion and free motion aeroelastic tests on a new concept dynamometric section model of the Messina suspension bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics，2004，92（6）：441—462.

[5]    DIANA G，RESTA F，ROCCHI D. A new numerical approach to reproduce bridge aerodynamic non-linearities in time domain[J]. Journal of Wind Engineering and Industrial Aerodynamics，2008，96（10/11）：1871—1884.

[6]    王骑. 大跨度桥梁断面非线性自激气动力与非线性气动稳定性研究[D].  成都：西南交通大学，2011：53—70.

WANG Q. The study on nonlinear motion-induced aerodynamic force and nonlinear aerodynamic stability of long-span bridge girder[D].  Chengdu：Southwest Jiaotong University，2011：53—70. （In Chinese）

[7]    唐煜. 流线型箱梁断面非线性自激力与非线性颤振响应研究[D].  成都：西南交通大学，2015：55—63.

TANG Y. Nonlinear self-excited forces of streamlined box deck and nonlinear flutter response[D].  Chengdu：Southwest Jiaotong University，2015：55—63. （In Chinese）

[8]    熊龙，王骑，廖海黎，等. 振幅对流线型箱梁自激气动力的影响[J].  实验流体力学，2017，31（3）：32—37.

XIONG L，WANG Q，LIAO H L，et al. Influence of vibration amplitude on motion-induced aerodynamic force of a streamline box girder[J].  Journal of Experiments in Fluid Mechanics，2017，31（3）：32—37. （In Chinese）

[9]    LIN S Y，WANG Q，NIKITAS N，et al. Effects of oscillation amplitude on motion-induced forces for 5 ：1 rectangular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics，2019，186：68—83.

[10]  GAO G Z，ZHU L D，HAN W S，et al. Nonlinear post-flutter behavior and self-excited force model of a twin-side-girder bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics，2018，177：227—241.

[11]  ZHANG M J，XU F Y，ZHANG Z B，et al. Energy budget analysis and engineering modeling of post-flutter limit cycle oscillation of a bridge deck[J].  Journal of Wind Engineering and Industrial Aerodynamics，2019，188：410—420.

[12]  NODA M，UTSUNOMIYA H，NAGAO F，et al. Effects of oscillation amplitude on aerodynamic derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics，2003，91（1/2）：101—111.

[13]  祝志文，陈政清，顾明. 薄平板气动导数的数值仿真技术[J].  湖南大学学报（自然科学版），2005，32（5）：11—15.

ZHU Z W，CHEN Z Q，GU M. Evaluation flutter derivatives of the thin plate by applying the numerical simulation method [J].  Journal of Hunan University（Natural Sciences），2005，32（5）：11—15. （In Chinese）

[14]  陈政清. 工程结构的风致振动、稳定与控制[M]. 北京：科学出版社，2013：602—610.

CHEN Z Q. Wind-induced vibration，stability and control of engineering structures [M]. Beijing：Sciences Press，2013：602—610. （In Chinese）

[15]  祝志文，夏昌. 基于两种湍流模型的橋梁颤振导数识别研究及比较[J].  湖南大学学报（自然科学版），2010，37（11）：6—11.

ZHU Z W，XIA C. Comparative study of two turbulence models based on the identification of flutter derivatives of bridges [J].  Journal of Hunan University（Natural Sciences），2010，37（11）：6—11. （In Chinese）

[16]  于向东，陈政清. 桥梁主梁断面颤振导数的强迫振动识别法[J].  中国公路学报，2001，14（2）：36—39.

YU X D，CHEN Z Q. Forced vibration method for identifying flutter derivatives of bridges sectional modal [J].  China Journal of Highway and Transport，2001，14（2）：36—39. （In Chinese）

[17]  THEODORSON T. General theory of aerodynamic instability and mechanism of flutter[R]. Washington：National Advisory Committee for Aeronautics，1935：291—311.

[18]  刘小兵，陈政清，刘志文. 桥梁断面颤振稳定性的直接计算法[J].  振动与冲击，2013，32（1）：78—82.

LIU X B，CHEN Z Q，LIU Z W. Direct computation method for flutter stability of bridge deck [J].  Journal of Vibration and Shock，2013，32（1）：78—82. （In Chinese）

[19]  刘志文，谢普仁，陈政清，等. 大跨度流线型箱梁悬索桥颤振稳定性气动优化[J].  湖南大学学报（自然科学版），2019，46（3）：1—9.

LIU Z W，XIE P R，CHEN Z Q，et al. Aerodynamic optimization of flutter stability for a long-span streamlined box girder suspension bridge [J].  Journal of Hunan University（Natural Sciences），2019，46（3）：1—9. （In Chinese）