峡谷和垭口地形条件下输电线路风偏特性

刘春城，孙红运

(东北电力大学 建筑工程学院，吉林 吉林 132012)

我国是一个多山国家，两条山脉并排形成峡谷和垭口是常见的山地地形。峡谷和垭口会形成的天然通道，受狭管效应[1]的影响，风速显著增大。对于跨越峡谷和垭口的输电线路而言，风的加速效应会导致导线风荷载加大，对线路风偏产生不利影响。目前针对山地地形中输电线路抗风偏设计，我国规范相关规定比较简单，没有详细考虑到一些地形因素(如山脉长度，山脉坡度，山脉间距)的影响。仅规定线路跨越峡谷、河道或位于暴露的山脊、顶峰等线路区段，其风速值应适当增加，如无可靠资料时，一般可按附近平地风速增加10%[2]来考虑。这种过于笼统的规定会导致风偏计算结果与实际相差较大，不利于线路安全运行。

国内外学者针对山地风场下输电线路风偏研究很少有涉及，大多数关于输电线路风偏响应的研究都基于平坦地貌边界层风场[3-8]。Bullard等[9]研究了峡谷走向对气流运动趋势的影响。Bowen等[10-12]研究了山体坡度，风向角，山体粗糙度等因素对加速效应的影响，但山体模型都是过于简单的山丘，并未考虑山体长度。孙毅等[13]提出了新的脉动风及平均风分布模型。李正良等[14]提出了复杂山地风场平均及脉动风速均方根计算修正模型。李天昊等[15-19]较系统地研究并分析了峡谷长度、山顶间距、山脉坡度3种地貌因素对平均风加速效应的影响。总的来看，目前对于山地线路风偏的研究过于简单笼统，并未考虑地形因素。因此获得不同地形因素下峡谷和垭口输电线路风速特性，准确计算线路的风偏响应，对于架设在山地中输电线路抗风偏设计具有重要的借鉴和指导意义。

本文建立了不同地形因素下峡谷和垭口风场，得到线路各点的平均横向和竖向风速随山脉地形因素的变化规律。计算了线路在山地风速和平地风速下的风偏响应，通过风偏角增大百分比来量化山地地形对线路风偏的影响。最后，用响应面方法得到山脉长度、坡度、间距三种因素和风偏角增大百分比的二次回归方程，并得到最不利地形的参数。研究结果为指导山地地形下输电线路抗风偏设计提供技术参考。

1 峡谷和垭口地形风场的数值模拟

1.1 峡谷和垭口地形模型

本文山体横断面选用余弦型山体。峡谷和垭口的三维模型及线路走向如图1和图2所示。其中：H表示山体高度(本文中山体高度统一取100 m)，D表示山脉底部直径，则山脉的坡度可表示为2H/D。

图1 峡谷模型Fig.1 Canyon model

图2 垭口模型Fig.2 Puerto model

1.2 CFD数值模拟

1.2.1 计算域及网格划分

利用ANSYS软件中的SPACECLAIM建立峡谷和垭口模型，并用ICEM划分网格。其中计算域高度为6倍模型高度，计算域长度：山前取3倍模型长度，山后取5倍模型长度，宽度为3倍模型迎风宽度[20-21]。计算域采用结构化六面体网格，山体表面最大网格尺寸为5 m，增长率为1.1，竖向网格首层高度取为1 m，增长率为1.05。计算域模型及网格划分如图3所示。

(a) 计算域模型

1.2.2 入口边界条件

入口剖面包括平均风剖面和湍流风剖面，参照我国GB 50009—2012《建筑结构荷载规范》[22]中使用的指数率模型，平均风剖面的计算公式为

(1)

式中：U(z)为离地高度z处的平均风速;Ur为参考高度zr处的平均风速;α为地面粗糙度指数。

湍流风剖面计算包括湍动能和耗散率两个参数，为实现入口剖面的自保持性，对湍流动能k和耗散率ε分别采用式(2)和(3)来计算

k(z)=0.3[I(z)×U(z)]2

(2)

(3)

式中：k=0.42;Cμ=0.09;I(z)为z高度处湍流度;Lu为湍流积分尺度。

这两个参数均采用日本规范[23]中的公式：(Zg为梯度风高度，B类地貌下Zb=5 m)

(4)

(5)

1.2.3 其余参数

湍流模型采用Realizablek-ε湍流模型，选用非平衡壁面函数，计算域入口为速度入口，出口为自由出口，两侧和顶部为对称边界，平地和山体表面为固定壁面。其中Fluent软件中粗糙度高度(roughness height)ks与空气动力学中粗糙度长度Z0的换算关系为ks=20Z0，这里取山体和平地的粗糙高度分别为1 m和0.5 m。

2 输电线路参数和计算工况

2.1 输电线路参数

线路走向如图1或图2中所示，采用“耐张塔-直线塔-直线塔-耐张塔”组成三跨线路，跨内无转角。线路电压等级为500 kV，B类地区，基本风速v0为30 m/s，耐张塔呼称高36 m，直线塔呼称高39 m，导线型号4×LGJ-400/35，绝缘子型号XWP2-160。为便于比较不同地形导线各点风速，每档导线均划分45个单元，整条线路节点个数为136。

2.2 导线风荷载及风偏响应模拟

在有限元软件中模拟导线风偏时，将4分裂导线等效为一根导线，并将截面积、风荷载等参数做等效化处理。将导线离散成多段索单元，计算每个单元所承受的风荷载，作为静力施加到节点上。每个单元所受风荷载计算公式

(6)

式中：Fx为单元所受风荷载;vh为单元所在高度h处的风速;μsc为导线体型系数，取1.1;βc为风荷载系数，计算风偏时取1;d为导线直径;l为单元长度。

2.3 计算工况

为定量分析山地风场下加速效应对绝缘子风偏位移的影响，本文设置2种计算工况。

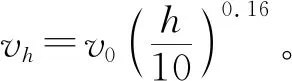
工况二：风速vh取峡谷和垭口地形的横向风速。

基于不同工况下直线塔绝缘子串风偏角，定义风偏角增大百分比为

η=(θ2-θ1)/θ1

(7)

式中，θ1，θ2分别为工况1，2的直线塔绝缘子风偏角计算结果。

3 峡谷地形输电线路风偏特性

3.1 模型工况

峡谷指的是山顶间距(W)大于或等于山脉底部直径(D)的地形。此种地形下研究的地貌因素包括山脉长度，山顶距离，山脉坡度。所有涉及到的数值模拟地形工况如表1所示。

表1 峡谷模型参数Tab.1 Canyon model parameters

3.2 线路架设位置

输电线路在横跨峡谷时，可能架设在山脉中的任意位置。当风向为顺峡谷时，由于峡谷中风场的复杂性，不同位置处的线路所承受的风速也不同。因此，在山脉长度300 m的峡谷中每隔50 m架设一条线路，共七条线路，如图4所示。每条线路所在位置横向风速由图5所示。图中边跨和靠近山顶处的线路风速随着到入口距离的增加先减小后增大。在距离入口200 m处达到最小，这是因为由于风越过山顶后是一段平坦的山脉，且这两部分的线路距离山体表面较近，空气的流动受山体表面摩擦的影响较大，导致线路上风速的减小。但是在峡谷的后半段线路上风速却在增大，这是因为空气穿过峡谷后是开阔的平地，有利于峡谷中空气的流出，所以导致后半段的风速会有小幅的提升。线路中跨中点处的风速并非在入口处最大，而是在距入口50 m处最大，这是因为峡谷中轴线上的风速在入口处仍然处在一个加速的过程，在50 m处达到最大，而后由于山体的摩擦逐渐变小。综合边跨和中跨的风速来看，在距离入口150～200 m处线路风速最小，但是由于风向的不确定性，建议在线路选线时在峡谷中部跨越峡谷更为保守。峡谷入口处风的加速效应最大，所以入口处线路是风偏最不利的线路，也是受地形因素影响最大的位置。因此在研究峡谷地形因素的影响时，线路的位置均架设在峡谷入口处。

图4 线路架设位置Fig.4 Line erection position

3.3 山脉长度的影响

3.3.1 山脉长度对风场的影响

不同的山脉长度会对来流风的加速效应产生不同影响，处于峡谷入口的线路也会根据山脉长度的不同而承受不同的风速。不同山脉长度入口处输电线路所受横向风速，及平地风速如图6所示。由图6可知，峡谷对风的加速效应很明显，相同高度时，峡谷中输电线路所受风速要高于平地风速。随着峡谷长度的逐渐增大，峡谷对风的加速效应逐渐减小，线路所承受的风速也逐渐变小。图中山脉长度在达到300 m后，间隔从100 m变成300 m时风速的变化与之前相同，说明山脉长度的影响在逐渐减小，最后趋于稳定。因此在山脉长度达到一定程度后，再增加长度也不会对风速产生影响。不同山脉长度输电线路所受竖向风速，及平地竖向风速如图7所示。由图7可知，不管峡谷长度多少，整条线路的竖向风速都很小，最大处仅有3.8 m/s，这是因为当风向为顺峡谷时，峡谷的受风面积小，流动的空气可以顺利从山脉两侧绕过去，不会产生大面积的爬升。因此，整条线路上的竖向风加速效应不显著。

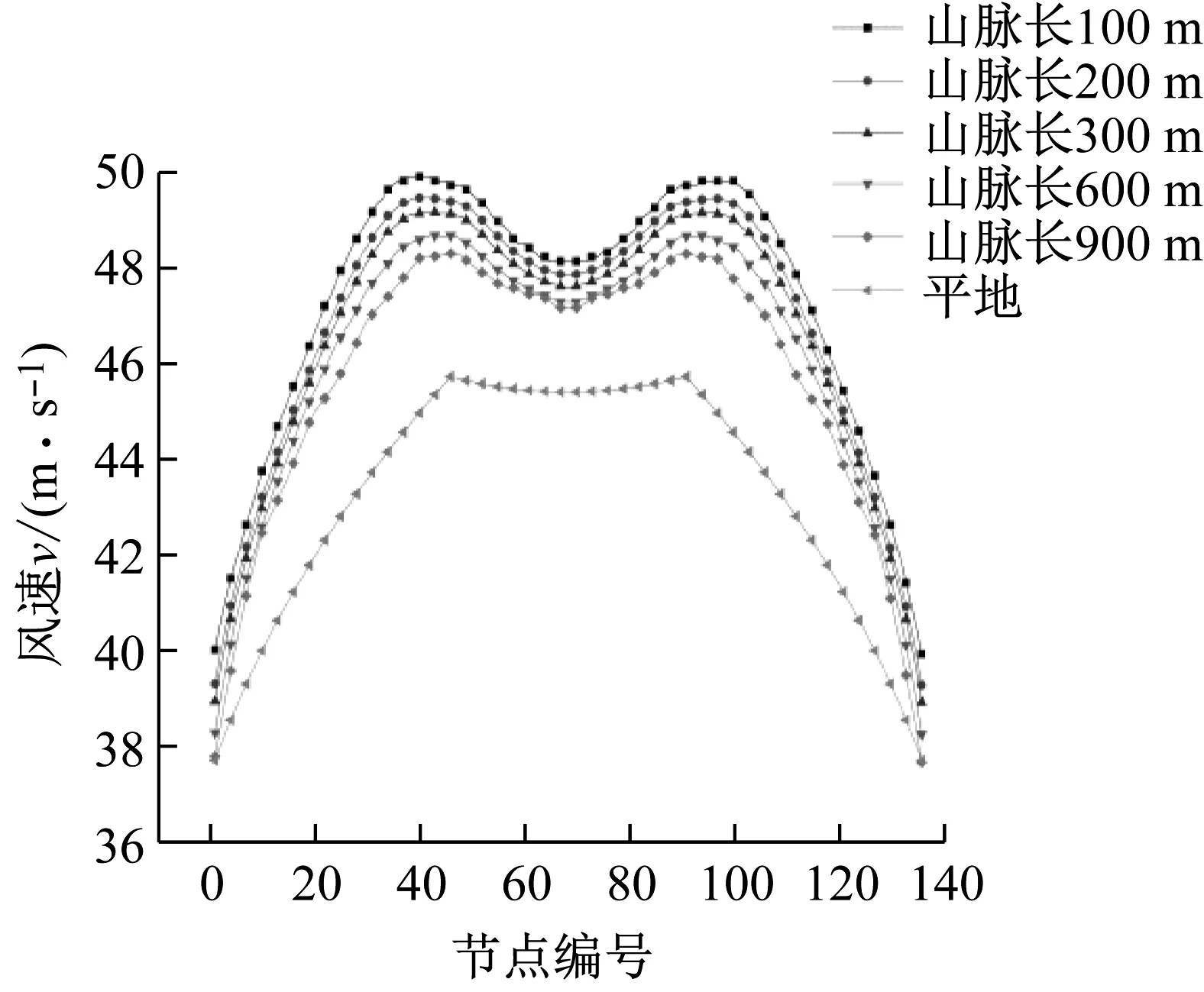
图6 不同山脉长度横向风速Fig.6 Cross wind speeds of different mountain lengths

图7 不同山脉长度竖向风速Fig.7 Vertical wind speeds of different mountain lengths

3.3.2 山脉长度对线路风偏的影响

由图6可知，峡谷风速要大于平地风速，在此基础上，可以进一步计算出不同山脉长度下输电线路风偏角增大百分比的变化情况。如图8所示，在山脉长度为100 m时，山顶直线塔的风偏角要比平地大7.58%，当山脉长度增大时，风偏角增大百分比变小。说明山脉长度越长，峡谷地形对线路风偏的影响越小。

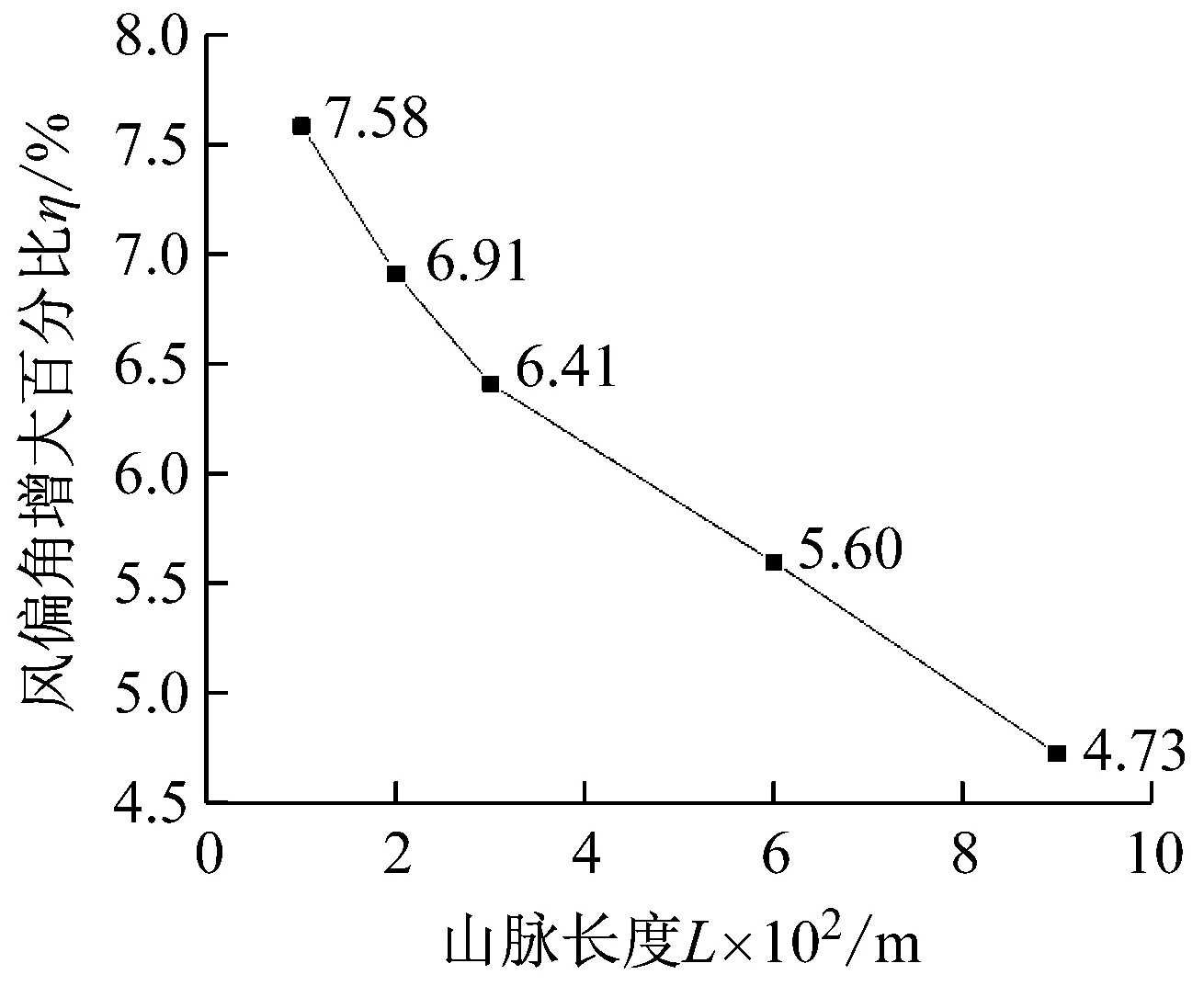
图8 不同山脉长度的风偏角增大百分比ηFig.8 The η of different mountain lengths

3.4 山顶间距的影响

3.4.1 山顶间距对风场的影响

山顶间距也会对峡谷内风场产生影响，导致峡谷内输电线路所承受的风速有所差异。不同山顶间距线路横向风速，及平地风速如图9所示。当山顶间距变化时，线路边跨上的风速不变，说明峡谷中两个山脉之间的距离并不影响山脉外侧的风场。而对于线路中跨，风速随着山顶间距的增大而减小。造成这种结果的原因一方面是由于山顶间距越大，线路档距增大，导线弧垂越大，导线高度变小，风速就会变小。另一方面是因为山顶间距变大，导致峡谷中的空间更加开阔，对风的加速效应减小，风速变小。对比峡谷风速和平地风速可以发现，不同山顶间距时，数值模拟的风速结果变化更大，印证了山脉间距会对峡谷内风场产生影响。不同山顶间距线路竖向风速，及平地风速如图10所示。由图可知，不论山顶间距多大，线路上的竖向风速都很小，因此整条线路上的竖向风加速效应不显著。

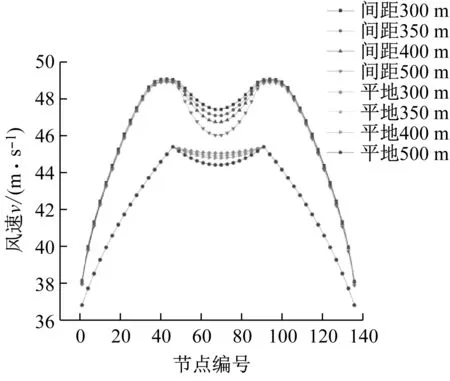
图9 不同山脉间距横向风速Fig.9 Cross wind speeds of different mountain spacing

3.4.2 山顶间距对线路风偏的影响

进一步计算山脉间距对线路风偏的影响，如图11所示。风偏角增大百分比随着间距的增大而减小，在两条山脉山脚相接时最大。间距从300 m增加到500 m时，η变化范围并不大，说明山脉间距对线路风偏的影响较小。

图11 不同山脉间距的风偏角增大百分比ηFig.11 The η of different mountain spacing

3.5 山脉坡度的影响

3.5.1 山脉坡度对风场的影响

本小节研究峡谷中不同山脉坡度对风场的影响，本文是通过改变山脉底部直径来改变坡度，而峡谷的定义是山顶间距W≥底部直径D。因此，在改变山脉底部直径的同时改变山顶间距，使W=D，即两条山脉的山脚相接。不同山脉坡度线路横向风速，及平地风速如图12所示。线路边跨的风速随着山脉坡度的减小而减小，这是因为坡度越小，地势越平缓，对风的加速效应越小。而山顶的风速随着坡度的减小先增大后减小。出现这一结果是因为山顶的风速是由山脉体型和山脉坡度共同作用的。一方面坡度的变化会导致山脉体型的变化，坡度越大，山体越显得细长，空气就越容易在山的两侧产生绕流，而很难爬升到山顶。坡度越小，山体越显得宽厚，空气不易绕流，继续爬升到山顶而导致山顶风速变大，在底部直径为400 m时达到最大。另一方面随着坡度减小到一定程度，平缓的地势对山顶的风速起到了主导作用，因此山顶风速会越来越小。线路中跨在靠近山脉的部分与山顶风速规律和原因基本相同。而线路中跨中间部分随着山脉坡度的减小而减小，一方面由于山顶间距越大导致导线弧垂越大，导线高度越小，风速越小。另一方面坡度越小，峡谷内的空间越大，狭道的加速效应越小导致风速变小。不同山脉坡度线路竖向风速，及平地风速如图13所示。不论山脉坡度多大，线路上的竖向风速都很小，因此整条线路上的竖向风加速效应不显著。

图12 不同山脉坡度下的横向风速Fig.12 Cross wind speed of different mountain slopes

图13 不同山脉坡度下的竖向风速Fig.13 Vertical wind speed of different mountain slopes

3.5.2 山脉坡度对线路风偏的影响

进一步计算山脉坡度对线路风偏的影响，如图14所示。各个坡度的风偏角增大百分比，随着坡度的逐渐减小先变大后减小，在直径为300 m时达到最大，说明当峡谷的山脚相接时，山脉的坡度为2/3时，对线路风偏的影响最大。

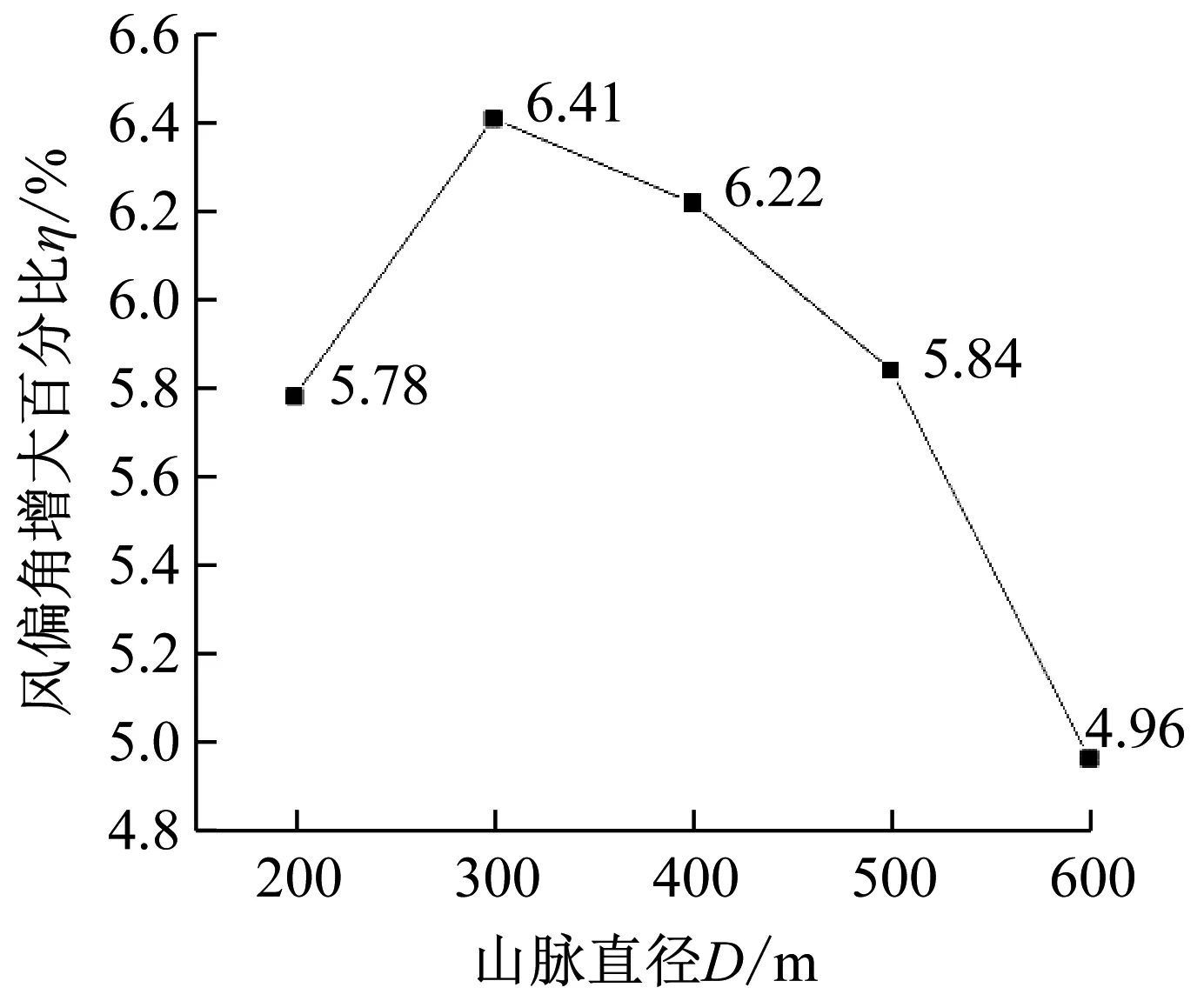
图14 不同山脉坡度的风偏角增大百分比ηFig.14 The η of different mountain slopes

4 垭口地形输电线路风偏特性

4.1 模型工况

垭口地形指的是山顶距离W小于山底直径D的地形，不同于峡谷之处是两个山脉交叠在一起，在山脉之间形成一个低凹的地势。此种地形下研究的地貌因素包括山脉长度，山顶间距，山脉坡度。所有涉及到的数值模拟地形工况如表2所示。

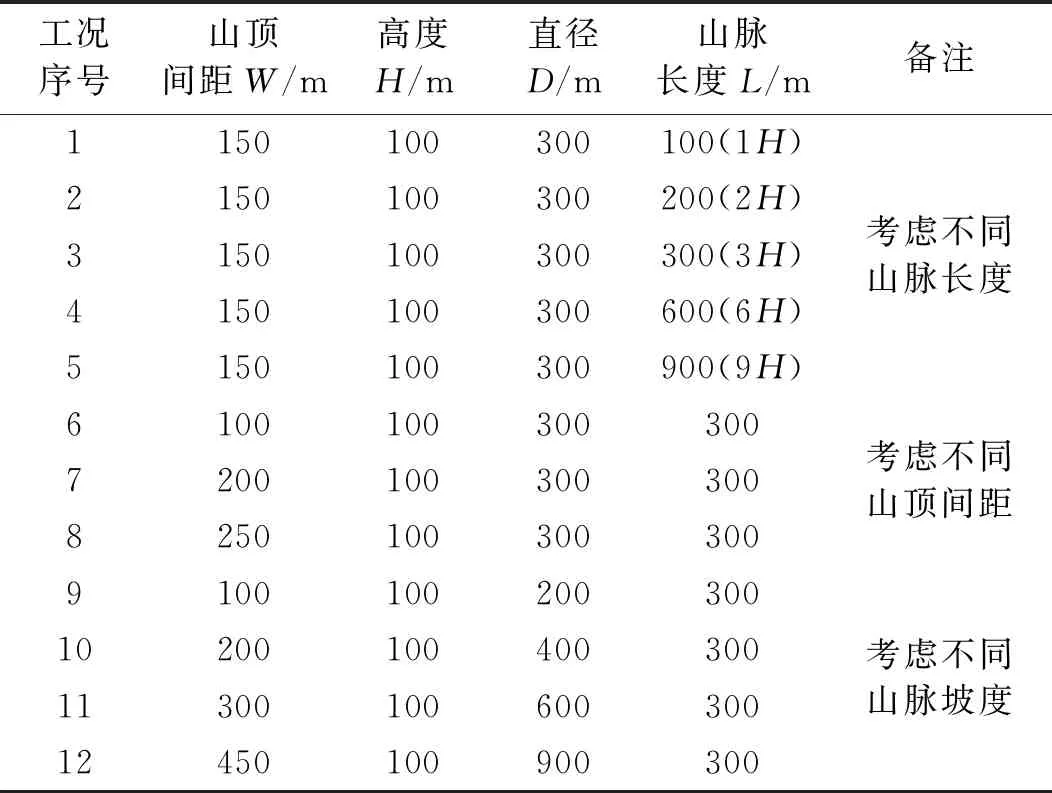
表2 垭口模型参数Tab.2 Puerto model parameters

4.2 线路架设位置

线路可在任意位置跨越垭口，风向为顺垭口时，垭口中不同位置的线路风速也不同。在山脉长300 m的垭口地形中，每隔50 m架设一条线路共7条线路，如图15所示。每条线路所在位置横向风速如图16所示。虽然垭口地形两山间距相比峡谷变小了，但是图中线路边跨，山顶风速规律与峡谷基本相同，都是先减小再增大，在距入口200 m时最小，其原因也同峡谷一样，在此不再赘述。说明两山之间的间距并不影响山脉外侧的风场。线路中跨中间部分与峡谷不同，在入口处风速最大，然后依次减小。原因是垭口地形两条山脉距离很近，导致低凹处空间狭小。且导线架设处距离山体很近，使在两侧山体绕流的空气更加迅速的吹向导线。来流风吹向垭口时，空气迅速涌进入口导致入口风速突增，然后由于山体的摩擦平稳减小。图中可以看到中跨中间部分风速会有一个小突起。这是由于山脉之间的交叠使低凹处形成一个夹角，由于此处空间过于狭小，使风速略大于周围，且在夹角上方一定高度内风速都会受到影响。而且这个突起会随着线路到入口距离的增加而变大，这是因为突起处导线距离山体表面较远，风速受山体摩擦的影响没有附近线路的大，导致风速差距越来越大。由于边跨和中跨导线到山体表面的距离相比于峡谷差别更小，所以风速受山体表面摩擦作用相近，风速变化的程度也想近。综合来看，线路跨越垭口时，在距入口200 m处的风速最小，但是由于风向的不确定性，架设在垭口中间更为保守。垭口在入口处风的加速效应最大，所以入口处线路是风偏最不利的线路，也是受地形因素影响最大的位置。因此在研究垭口地形因素的影响时，线路的位置均架设在垭口入口处。

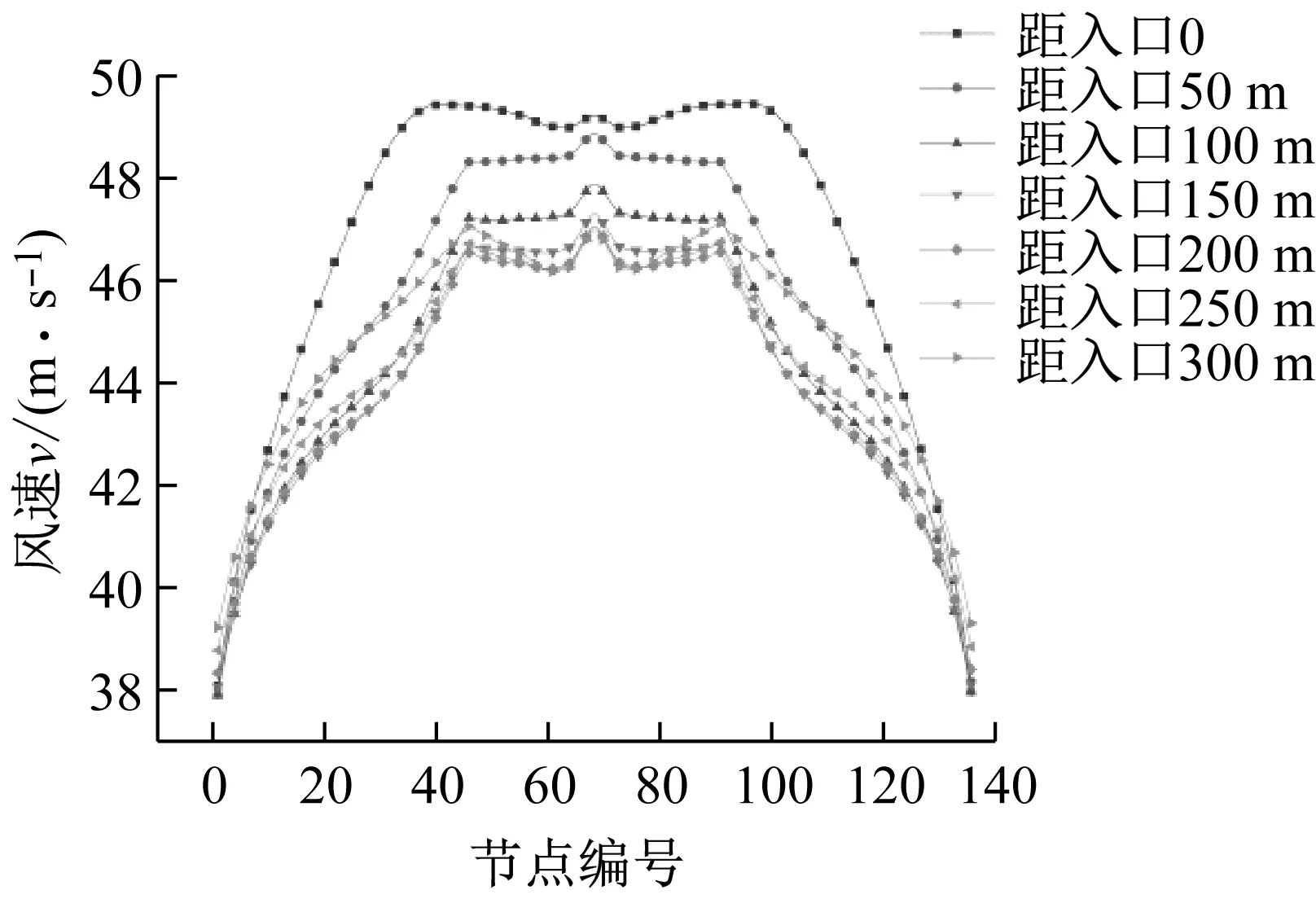
图16 线路各点风速Fig.16 Wind speed at each point of the line

4.3 山脉长度的影响

4.3.1 山脉长度对风场的影响

不同山脉长度入口处输电线路所受横向风速，及平地风速如图17所示。由图可知，与峡谷地形风速相比，峡谷的中跨风速要比山顶略小，而垭口地形线路中跨风速与山顶风速基本相同。但是风速变化规律和峡谷相同，都是随着山脉长度的增加而减小。图中山脉长度由100 m到200 m时，风速减小的程度略大于其他。说明垭口的长度不大时，长度的变化对风的加速效应更加敏感。不同山脉长度入口处输电线路所受竖向风速，及平地风速如图18所示。垭口的竖向风速相比于峡谷地形，虽然中跨导线更接近于山体，使竖向风速略有增加，但是最大竖向风速也仅有4.9 m/s，所以竖向风加速效应不显著。

图17 不同山脉长度横向风速Fig.17 Cross wind speeds of different mountain lengths

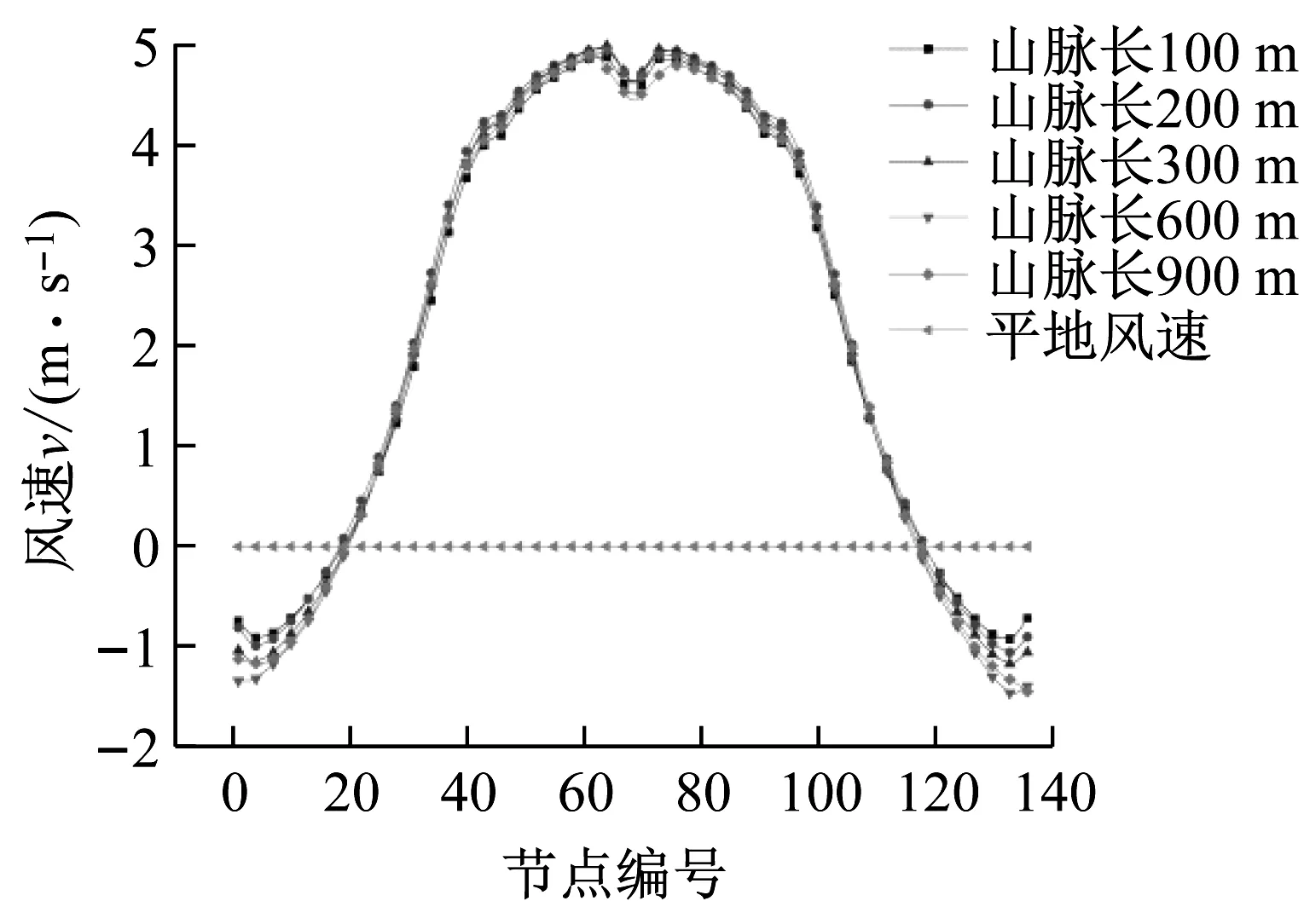
图18 不同山脉长度竖向风速Fig.18 Vertical wind speeds of different mountain lengths

4.3.2 山脉长度对线路风偏的影响

计算出垭口不同山脉长度下输电线路风偏角增大百分比的变化情况。如图19所示，在山脉长度为100 m时，山顶直线塔的风偏角要比平地大7.92%，当山脉长度增大时，风偏角增大百分比变小。且曲线逐渐趋于平缓，随着山脉长度的增加，风偏角增大百分比会趋近与一个固定值。

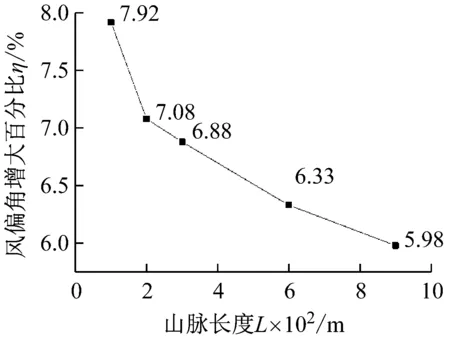
图19 不同山脉长度的风偏角增大百分比ηFig.19 The η of different mountain lengths

4.4 山顶间距的影响

4.4.1 山顶间距对风场的影响

不同山顶间距线路横向风速，及平地风速如图20所示。图中可以看出线路边跨的风速并不随着间距的变化而改变，说明垭口地形山脉之间的间距不影响山脉外侧的风场，这一点和峡谷地形相同。线路整个中跨的风速随着间距的增大而减小，出现这个结果的原因一部分是由于中跨的弧垂随着档距的增大而增大，导致导线高度减小风速减小。但是对比平地风速变化的程度，垭口的风速变化范围更大，这是由于地形变化导致的。间距的增大，导致垭口低凹处空间变开阔，对风的加速效应减小。随着垭口间距的逐渐变小，线路中跨的风速越来越接近山顶的风速。这是因为间距的减小使垭口内地表的高度不断升高接近山顶，使垭口看起来更像是一个孤立山脉，所以导线风速更接近于山顶。间距很小时，导线中跨中间的风速有一个小突起，但随着间距的增大突起逐渐消失直至凹陷。这是由于山体二维轮廓形状的特性导致的，间距越小，山体交叉点的高度越高，山体轮廓的斜率越大，导致低凹处的夹角越小。由4.2节可知，低凹处的夹角会导致其上方一定高度内风速略大于周围风速。但随着间距的增大，山体轮廓逐渐平缓，交叉处的夹角也变大，且导线距离夹角的高度变高，所以，交叉处对于导线风速的影响变小。不同山顶间距线路竖向风速，及平地风速如图21所示。图中可以看出山顶间距最小时线路竖向风速最大，但仅有5.2 m/s，所以竖向风加速效应不显著。

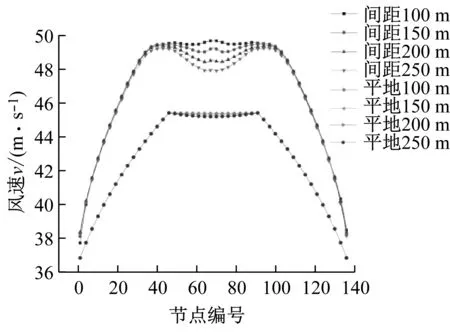
图20 不同山脉间距横向风速Fig.20 Cross wind speeds of different mountain spacing

图21 不同山脉间距竖向风速Fig.21 Vertical wind speeds of different mountain spacing

4.4.2 山顶间距对线路风偏的影响

不同山顶间距的风偏角增大百分比如图22，在山顶间距100 m时达到最大，随着间距的增大，η逐渐变小。但是垭口的风偏角增大百分比普遍大于峡谷地形，说明垭口对线路风偏的影响更加明显。

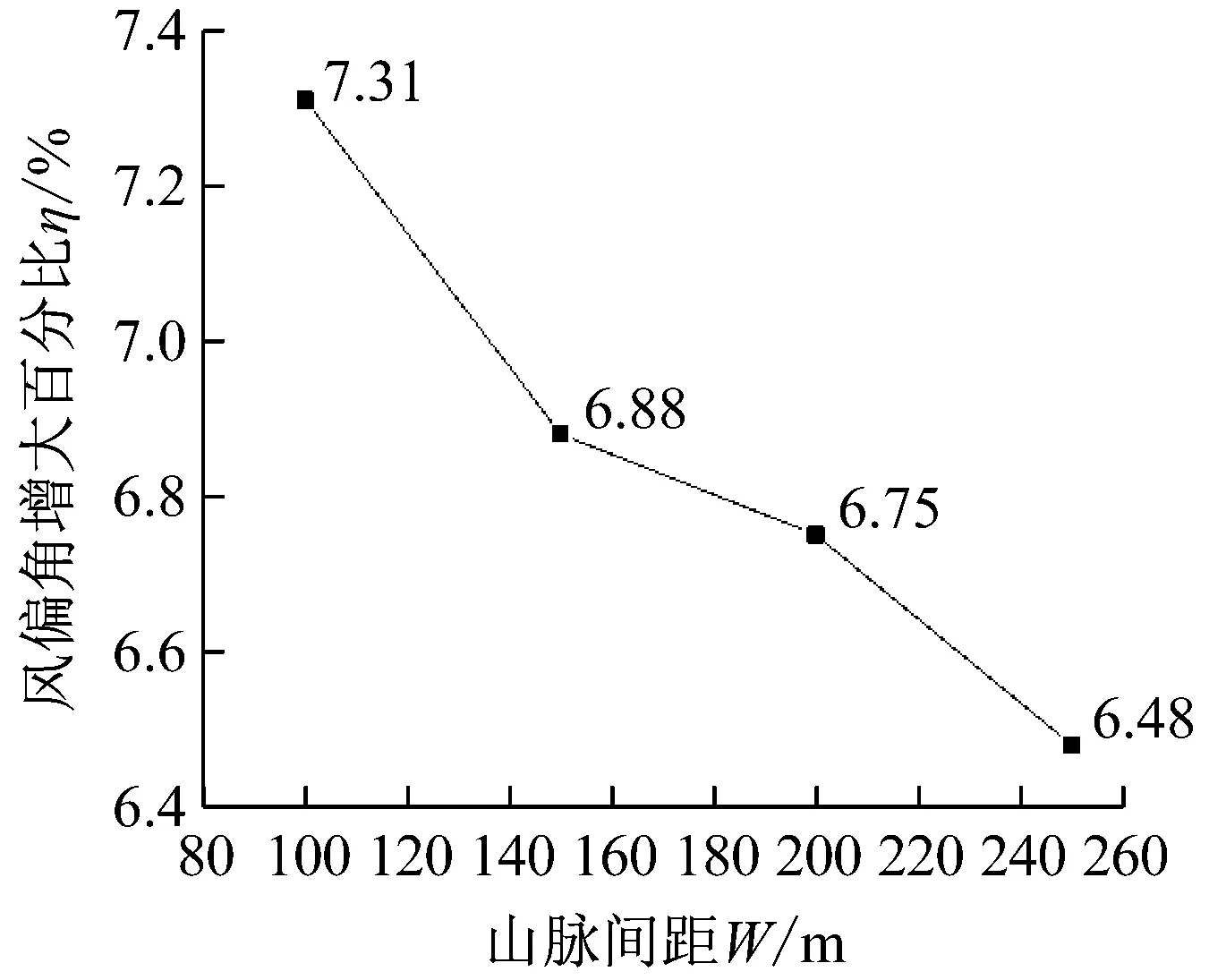
图22 不同山脉间距的风偏角增大百分比ηFig.22 The η of different mountain spacing

4.5 山脉坡度的影响

4.5.1 山脉坡度对风场的影响

对于垭口地形，山脉坡度的改变将影响整个垭口的形状。因此为了排除不同山顶间距的影响，将每个模型的山顶间距取底面直径的一半，即每个模型两条山脉的交点都在50 m高度处。不同山脉坡度线路横向风速，及平地风速如图23所示。图中横坐标采用和峡谷同样的方法表示。线路边跨风速随着坡度的减小而减小，这是因为坡度越小，地势越平缓，对风的加速效应越小。甚至在底面直径900 m时，有一部分线路的风速要小于平地风速。虽然垭口两条山脉的距离相比峡谷来说很近，但是在山顶和山顶附近风速变化规律和峡谷相同，都是随着坡度的减小先增大在减小，在底面直径400 m时最大。说明山脉距离的改变并不影响山脉顶部及附近的风场，这一点与3.4.1中的结论相同。但是对于线路中跨中间部分风速，垭口和峡谷是有差异的。峡谷地形中此处风速随着坡度的增大而减小，垭口地形中是先增大再减小。这是因为峡谷地形中两条山脉并不相交，可以看成两个孤立山脉。线路中跨中部可以看做处于两条山脉中间，其下方和前方基本可以看做平地，所以此处的风速只与狭道的大小有关。但是对于垭口，两条山脉相互交叠，不可看做独立的山脉，而是一个整体。线路中跨中部处于山体中央，此处的风速受山脉坡度和山脉体型的共同影响。坡度越大，加速效应越明显，但是在山体坡度很大时，山体的体型很瘦小，遮挡面积很小，所以风速不会过大。随着底面直径的增加，遮挡面积变大，所以风速普遍变大。但是随着底面直径不断增大，山脉的地势越来越平缓，接近平地时，山脉坡度又起到了主导作用，风速会越来越小。综合山脉坡度和体型的影响，导致线路中跨中部风速在底面直径300～400 m时最大。不同山脉坡度线路竖向风速，及平地风速如图24所示。图中山脉坡度越大竖向风速越大，但是最大也只有5.2 m/s，所以竖向风加速效应不显著。

图23 不同山脉坡度下的横向风速Fig.23 Cross wind speed of different mountain slopes

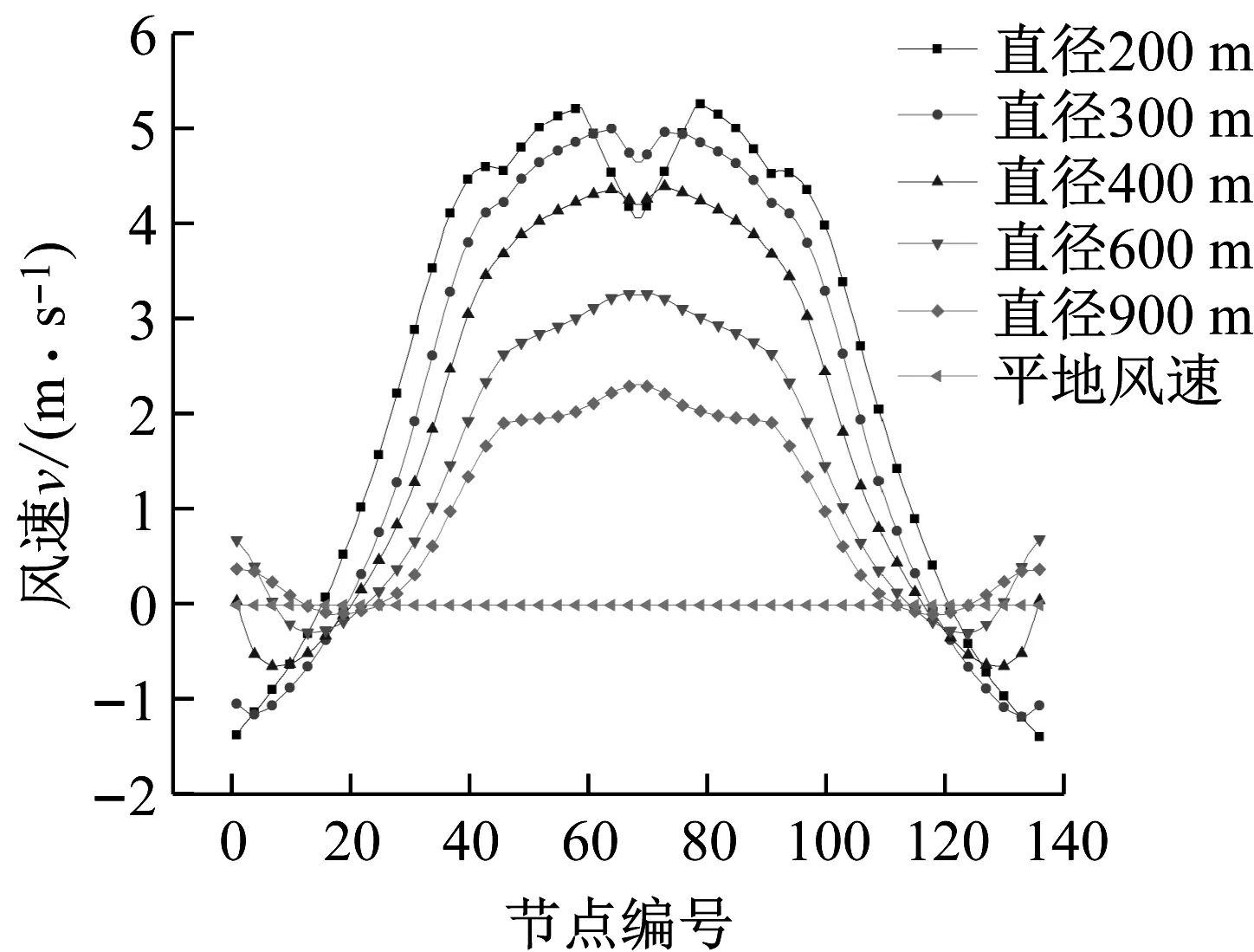
图24 不同山脉坡度下的竖向风速Fig.24 Vertical wind speed of different mountain slopes

4.5.2 山脉坡度对线路风偏的影响

不同山脉坡度的风偏增大百分比如图25，随着坡度的减小，η先增大再减小。当两条山脉山顶间距为底面直径一半时，山脉坡度为2/3时，对线路风偏的影响最大。

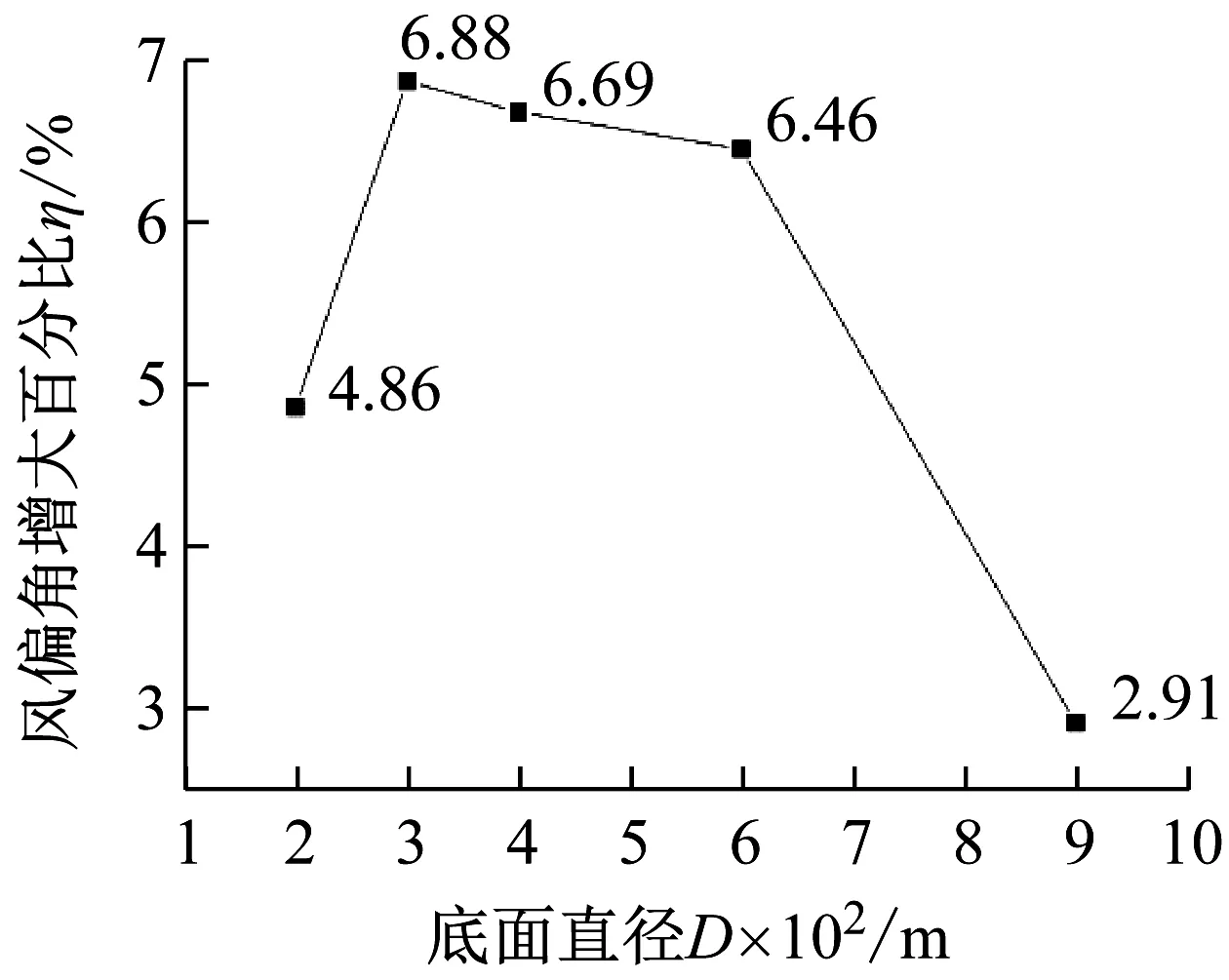
图25 不同山脉坡度的风偏角增大百分比ηFig.25 The η of different mountain slopes

5 地形因素与风偏角增大百分比η的响应面分析

5.1 响应面回归方程的建立

由于现实中山地地形复杂多变，无法通过数值模拟计算出每个地形的η。因此本文采用Box-Behnken方法进行仿真工况设计，以风偏角增大百分比为响应值(Y)，选用山脉长度(A)，山脉坡度(B)，山脉间距(C)为影响因素，其中山脉坡度用底面直径表示。运用Design-Expert软件进行多项拟合回归分析，得到二次响应面回归方程为

(8)

5.2 仿真分析因素及水平及仿真结果分析

仿真分析因素及水平见表3，响应面分析仿真结果见表4，响应面回归模型方差分析结果见表5。

表3 仿真分析因素及水平Tab.3 Simulation analysis factors and levels

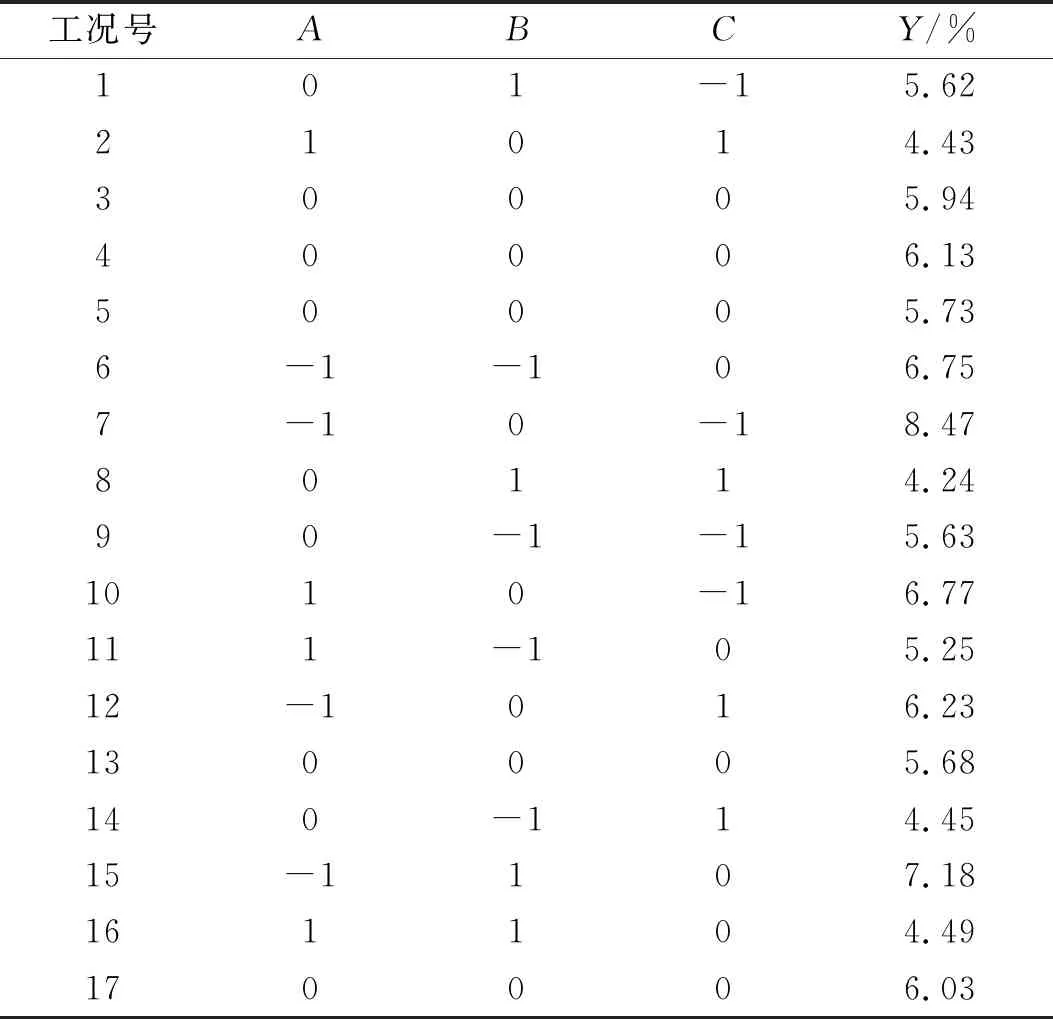
表4 仿真结果Tab.4 Simulation results

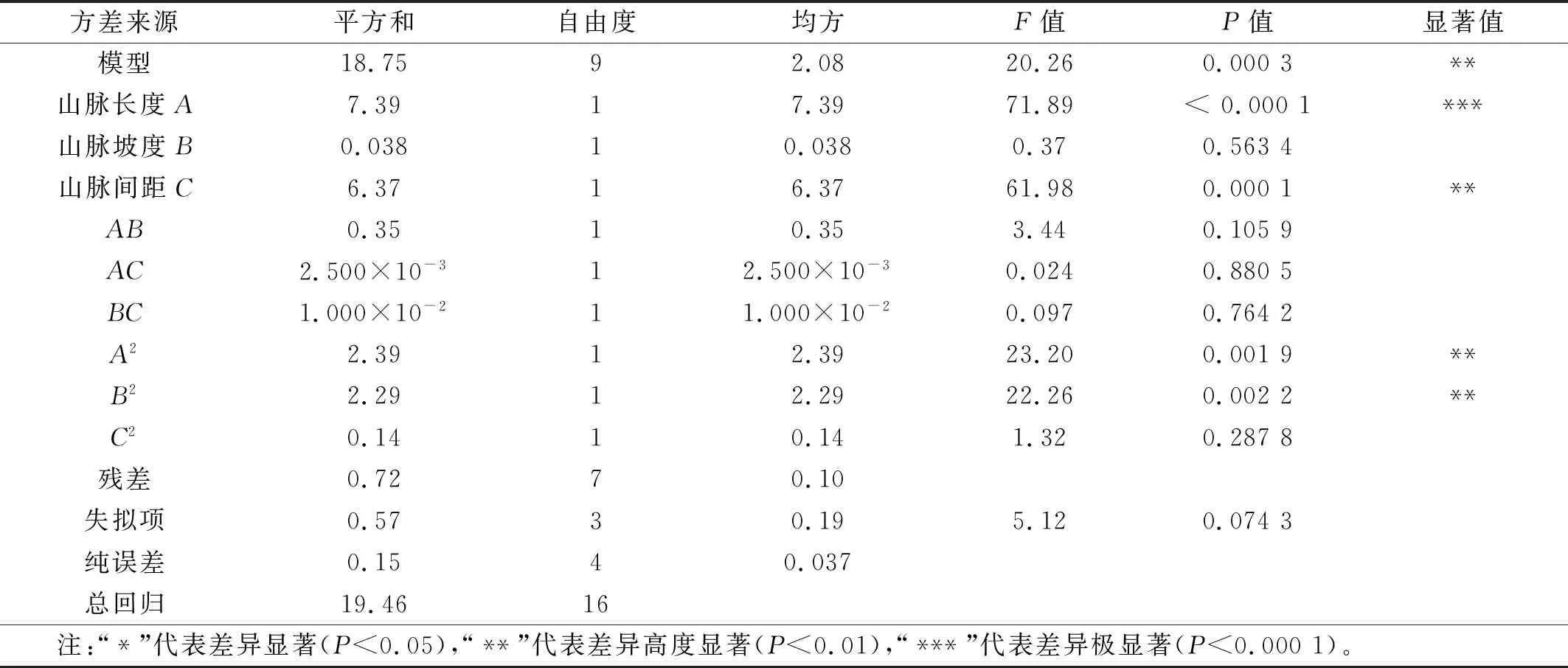
表5 回归模拟的方差分析Tab.5 Variance analysis of regression model

通过模型显著性检验(P<0.05)，表明该模型具有统计学意义。其自变量一次项A极显著(P<0.000 1)，C，A2，B2高度显著(P<0.01)。失拟项用来表示所用模型与仿真拟合的程度，P值0.074 3>0.05，无失拟因素存在，因此可用该回归方程代替仿真真实点对仿真结果进行分析。相关系数R2=0.963 0，AdjR2=0.915 5，均大于0.8，说明模型拟合优度较好。

5.3 各因素交叉相互作用分析

图26～28直观显示了各个因素交互作用的响应值，图中各因素的边线越平坦则该因素对风偏角增大百分比η的影响越小，边线越陡则该因素对风偏角增大百分比的影响越大[24]。图中显示，各因素的陡峭程度为A>C>B，与方差分析结果一致。

5.4 最大风偏角增大百分比

结合数值模拟和响应面分析结果，可以发现山脉长度越短，山脉间距越近越不利于线路风偏。由于本文设置了长度和间距的下限，所以根据回归模型得到最不利于线路风偏的地形参数为：山脉长度100 m，山脉坡度0.46，山脉间距100 m。最大风偏角增大百分比为8.33%。

6 结 论

(1) 线路跨越峡谷和垭口时，所受风速随着线路至山脉入口距离的增加，先减小后增大。所以山脉入口处风加速效应最为显著，不利于线路安全运行，建议线路从山脉中部跨越峡谷和垭口。

(2) 峡谷和垭口中线路上的竖向风速可以忽略不计。峡谷中η随着山脉长度，山脉间距的增大而减小，并且η会趋近与一个固定值。当山脉重叠部分相同时，η随着山脉坡度的减小先增大再减小，在坡度为2/3时最大。

(3) 垭口中η受地形因素的影响规律与峡谷相同，但是由于山脉间距更近，η值会普遍大于峡谷。

(4) 山脉长度、山脉坡度、山脉间距三种因素对风偏角增大百分比影响的灵敏度从大到小依次为山脉长度、山脉间距和山脉坡度。在本文研究的模型范围内，山脉长度100 m，山脉坡度为0.46，山脉间距100 m时，风偏角增大百分比达到8.33%。