基于多层感知机模型的天线方位角诊断
陈向荣
(中国移动通信集团福建有限公司,福建 福州 350001)
1 引言
随着移动互联网的高速发展,通过移动蜂窝网络接入互联网的用户数持续增长,用户对移动网络的需求日益增大,访问网络的数据量也随之高速增长,而且用户对网络质量的要求逐步提升。保障一个良好的网络环境,提高用户使用感知,成为移动网络优化工作的重中之重,这给网络优化的工作效率和质量的保证带来了巨大的挑战。在移动网络优化工作中,天线方位角的严重偏差将会很大程度上影响到网络优化效果和网络服务质量,作为日常网络优化基础数据的天线方位角,其准确性与否将直接导致网络优化质量的好坏。
当前,天线工参的数据大多依赖人工通过罗盘、坡度仪等工具进行测量,数据的准确性与工作人员的测量技术的熟练度和细心程度有很大的关系,时常出现数据的漏报和误报情况。过分依赖人工的检测,既无法保障测量数据的实时性,测量效率也很低。天线方位角作为天线工参中极为重要的一部分信息,核查的方法主要是通过工程优化人员到达基站现场,利用指南针贴近天线下沿进行方位角读取测量并手工记录,同时,结合室外天线、RRU(ra2io remote unit)和室内BBU(base ban2 unit)的线缆连接查询,最终完成小区的天线覆盖方向确认,而对于铁塔和壁挂类型的天线方位角的测量,则由持有登高证的工作人员对天线方位角进行确认,由此,天线方位角的测量和确认工作需要投入大量的人工成本,且数据的准确性和及时性无法保障。随着网络规模的日益增大以及多制式多频段多层网络的出现,持有登高证的工作人员核查天线方位角的工作量急剧增加,人工测量的方法已极大地影响网络维护、网络优化等工作的效率及质量,进而降低了用户使用网络感知,也增加了用户的投诉概率。如何利用大数据挖掘技术手段,实现天线方位角自动采集及异常预警,是当下亟须解决的问题。
2 多层感知机
2.1 多层感知机模型结构
多层感知机最主要的特点是有多个神经元层,因此也叫深度神经网络(2eep neural network,DNN)。第一层称为输入层,最后一层称为输出层,中间层称为隐层,其中,隐层的数量和输出神经元的个数可根据具体应用进行选择。3 层感知机的网络结构如图1 所示。
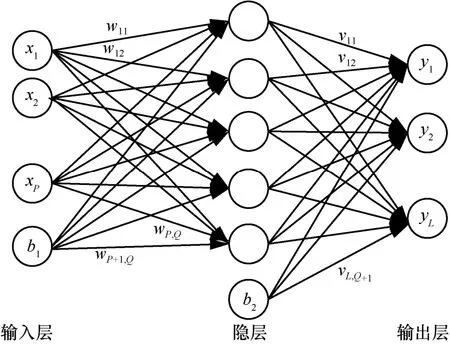
图1 3 层感知机的网络结构

前向传播即网络处于学习阶段,其学习过程为:首先,根据当前各层的权向量的值,对每个样本(即输入)作前向计算;然后,计算该网络的输出结果与期望值的差值,并与限定值进行比较,若小于限定值,则学习过程结束,否则反向传播逐层调整权向量值的大小,直到差值小于限定值。由此,多层感知机神经网络有以下几个优点:
• 对于具有高度非线性的问题,多层感知机神经网络能够以任意精度逼近任何非线性连续函数;
• 具有很强的容错性和很快的处理速度,因为在神经网络中信息是分布存储和并行处理的;
• 具有较好的泛化能力,因为神经网络在训练时,可以从输入和输出的数据中发现规律性的特征,并逐层调整各权值大小,具有较强的自学习和自适应能力;
• 具有较强的数据融合能力,多层感知机神经网络可以同时处理定量特征变量和定性特征变量;
• 无须考虑各个子系统间的解耦问题,MLP神经网络并没有明确限定隐层的数量和输出层神经元的个数,可根据实际应用选择相应的层数和输出层神经元的个数,因此对于单变量系统和多变量系统有通用的描述方式。
(2)促凝增强剂投加量的确定。取3号样品加入AP2.0%、水泥20.0%及相应添加剂,CA投加量不同,考察固化改良后浸出液主要指标,试验结果见表7。通过数据分析可以看出,当CA加量达到5.0%时,改良固化后的COD值较低47.5mg/L、抗压强度较高,达到1.76MPa。再增加加量固化效果变化不大,因此选择CA投加量为5.0%。
2.2 BP 算法
BP 神经网络的学习过程由信号的正向传播过程与误差的反向传播过程组成。正向传播过程是输入信号通过隐层和输出层节点的处理计算得到的网络实际输出值进一步与期望输出值进行对比,计算它们的差值,将其作为误差,若误差不在限定范围内,则转入学习过程的另一个阶段,即误差的反向传播过程。误差的反向传播过程是指将计算的误差通过隐层向输入层逐层地进行反传,并将误差分摊给各层的所有单元,以此作为调整各层权向量的值的根据,并反复地进行该过程。各层权向量的值不断修正的过程,即BP 神经网络的学习过程。在输出的误差值减小到限定范围内或迭代的次数达到限定学习的次数时,BP 神经网络的学习过程将会停止。
由此,BP 神经网络算法是把样本集学习与训练的问题转化为代价函数的无约束最优化问题。对于本文的3 层感知机网络,设该网络从(P+ 1)维输入空间RP+1到L维输出空间RL的非线性映射为:G:y=g(x),其中x=[x1,x2, …,xP]T为扩展的输入向量,y=[y1,y2, …,yL]T为输出向量。图1中的3 层感知机网络所对应的非线性映射G可收敛于在闭区间内的连续函数或非线性映射,这在参考文献[18-19]中得到了证明。假定训练样本集则感知机网络对该训练样本集进行学习,即寻找最优的各层网络权值,且在一定代价函数的条件下,非线性映射G是映射M的最优逼近,常用的代价函数表达式如下:
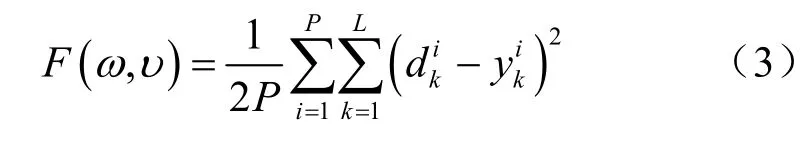
则上述最优化问题为:求使得代价函数到最小所对应的最优权向量ωopt和υopt的值,即:

对于3 层感知机网络的隐层网络,一般采用SBPM 算法调整权值。对于输出层网络,本文采用Kalman 滤波算法[20-21]调整权值。
BP 神经网络的学习过程主要有4 个步骤。
步骤1组成输入模式并由输入层通过隐层向输出层的正向传播过程,即BP 神经网络中的正向传播的过程。
步骤2计算网络实际输出值与期望值的差值,并作为误差,若误差不在限定范围内,则误差信号由输出层通过隐层向输入层逐层反向传播,从而调整各层权值的“误差反向传播”过程。
步骤3由“正向传播”与“误差反向传播”反复进行的网络“记忆训练”过程。该过程主要是不断更新各层权向量,直到找到最优权向量ωopt和υopt的值。
步骤4网络趋向收敛即网络的总体误差趋向极小值的“学习收敛”过程。
在训练阶段中,训练实例重复通过网络,同时修正各个权值,改变各层权值的目的是最小化训练集误差。继续网络训练直到此过程一直进行到网络输出的误差值减小到限定范围内或迭代的次数达到限定学习的次数时停止训练。因此,训练的终止条件可以为使网络收敛到最小的误差,也可以是设定的最大重复次数。本文BP 算法的具体流程如图2 所示。
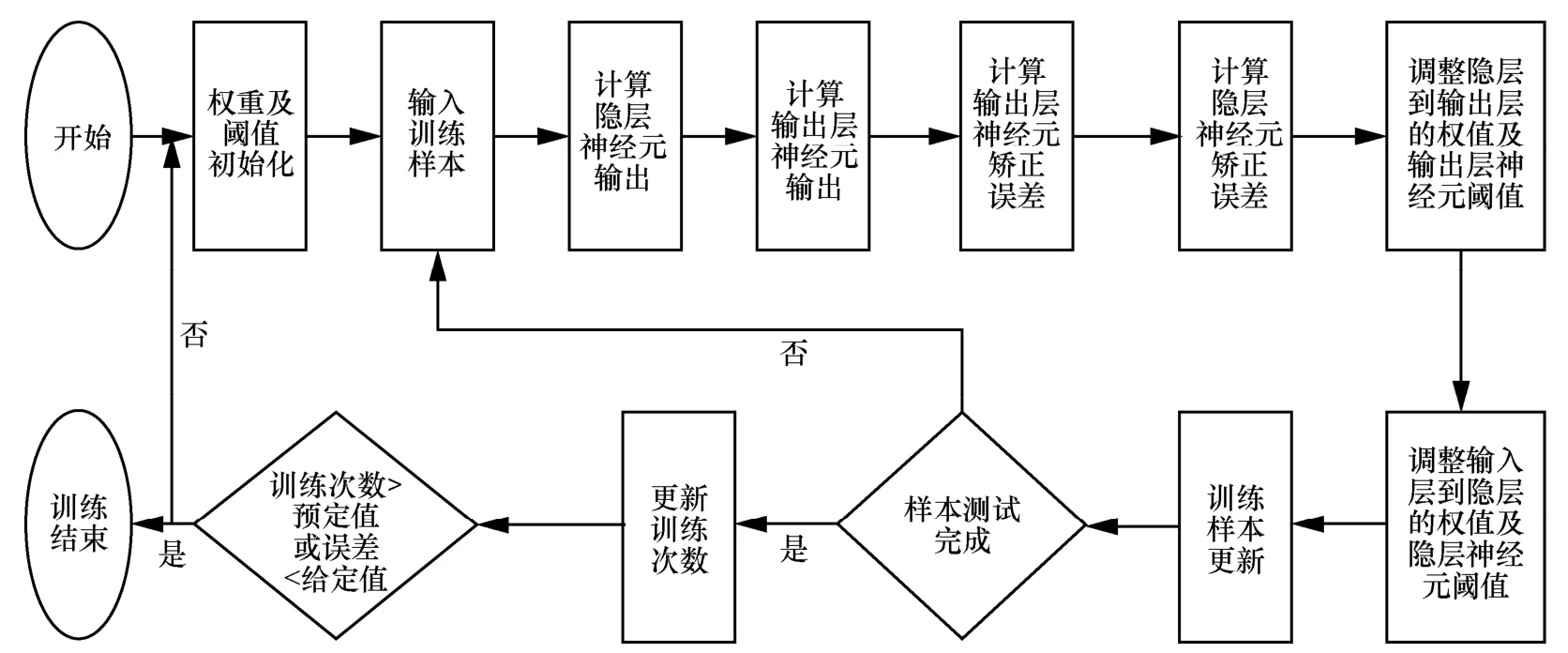
图2 BP 算法流程
3 数据实验与分析
3.1 实验设计
本文针对东南某省份2018 年1 月—6 月的OTT 数据和实际测量的天线方位角进行训练和测试,共计26 854 条数据。首先利用测量的方位角值将方位角方向划分为12 个区间,每个区间覆盖30°范围,进而构建分类标签;然后对数据进行栅格化处理;为了验证模型的预测效果,将数据集分为训练集和测试集两部分,其中训练集数据占比70%,共计18 798 条数据。最后,利用多层感知机深度神经网络算法,对训练数据集构建模型,并对测试集的方位角的方向类别进行分类预测。将预测结果与真实标签进行对比验证,评估模型效果。本文基于多层感知机的神经网络的天线方位角诊断流程如图3 所示。
3.2 数据预处理
每个小区的OTT 特征数据存在一定的差异性,其值的大小范围并不完全相同,且有的小区上报的采样点数量较多,有的则较少。为了能够将每个小区的特征数据转化为一条训练数据,则需要对每个小区的数据进行处理。首先对于各小区OTT 数据特征中和正常数据差别很大的少量异常数据,利用孤立森林(isolation forest,IF)算法进行识别并剔除;然后以小区经纬度为中心点构建大栅格,以距离小区经度或纬度的最大距离乘以2 作为大栅格的长度。对于每个小区900 个特征变量(不包含标签字段)的一条数据, 即30×30 的栅格,也可以看作大小为30×30 的图像。将大栅格按照30×30 划分成一个个小的栅格,并给每个栅格填充此栅格中分布采样点的RSRP 平均值,由于每个小区的RSRP 峰值并不相等,所以本文不采用常规的归一化方法,而是对每个小区单独进行处理。针对每个小区的栅格数据,将每个栅格的平均RSRP,除以最大的栅格平均RSRP,将栅格列表中的平均电平值数据单独取出,并组成向量,在900 个栅格中, 发现共有87个栅格有采样点分布。由于神经网络激活函数对处理数据的范围有要求,且在梯度下降的过程中,如果每个维度的数据分布不同,使用相同的学习率很难迭代到最优值。因此本文将栅格化的数据进行了归一化处理。
对于标签变量,本文将小区工参中的方位角按照正北方向为0°,并以顺时针方向计算,对方位角方向划分为12 个区间,每个区间覆盖30°范围,即“0”表示[0, 30°),“1”表示[30°, 60°),…,“11”表示[330°, 360°),以此构建天线方位角分类标签。数据预处理流程如图4 所示。

图3 基于多层感知机的神经网络的天线方位角诊断流程

图4 数据预处理流程
3.3 实验结果分析
本文基于预处理后的训练数据集利用多层感知机的反向传播算法构建天方位角诊断模型,并对测试数据集进行分类预测,得到准确率为92.6%,分类准确性较高。为了与本文基于多层感知机模型的天线方位角分类效果进行对比,这里还分别利用了常用的分类算法随机森林和逻辑回归两种算法对相同的数据集进行训练和测试,得到准确率分别为68.7%和73.4%。为了更清晰地了解12 类方位角基于多层感知机模型的预测效果,本文利用混淆矩阵计算各类别的查准率(Precision)、查全率(Recall)以及F1 得分(F1-score),从而对基于多层感知机深度神经网络算法预测的每类的结果进行了评估。评估结果见表1。

表1 基于多层感知机的天线方位角预测的评价指标
其中,查准率Precision = TP/(TP+FP),TP 表示真正例,即被模型预测为正的正样本,FP 表示假正例,即被模型预测为正的负样本,查全率Recall = TP/(TP+FN),FN 表示假负例,即被模型预测为负的正样本,F1 得分F-score =2×Precision×Recall /(Precision + Recall)。
由表1 可知,将天线方位角分为12 个区间,并利用多层感知机深度神经网络算法,对方位角进行诊断预测,整体效果较好,其中预测最差的类别为5(即方位角区间为[150,180°)),准确率为88.91%,召回率为80.33%,F1 得分为0.844 0,召回率略低,但比随机森林和逻辑回归两种算法的整体准确率都要高很多,预测最好的类别为10(即方位角区间为[300, 330°)),准确率为97.03%,召回率为95.89%,F1 得分为0.964 6。
4 结束语
本文基于多层感知机深度神经网络的方法对天线方位角的范围进行分类判别,分类准确率较高。结果表明,将天线方位角分为12 个类别,利用多层感知机的模型能够精准地预测天线方位角的范围类别。该方法已在东南某省份大数据平台上完成部署,并对现网的天线方位角进行诊断,取得了较好成果,该方法能够快速精准地识别异常天线方位角范围,为无线网络优化工作提供了有效的数据支撑。
为了更精准地核查效果,下一步将针对天线方向角的合理性给出建议值,在判断天线方位角是否偏移的同时考虑判断天线俯仰角是否偏移。

