一种动态特征匹配的部分重叠点云配准方法
杜辉,郑长亮,苗春雨,张小孟
(1. 北京电子科技职业学院电信工程学院,北京 100176;2. 杭州安恒信息技术股份有限公司,浙江 杭州 310051)
1 引言
随着无人机、激光雷达等技术的不断发展,建筑物、山地、医学、无人驾驶等场景都需要对实体进行三维重建[1-3]。三维重建研究中点的云配准与拼接技术是重点研究内容,随着用户对三维模型精度需求的提升,点云处理算法的可靠性要求也逐步提高。由于测量设备(如激光雷达)很难一次性完成对一个三维物体的点云数据采集,因此需要在多个角度分别采集三维物体的不同面,最后将不同角度采集的点云配准、拼接,才能得到一个完整的三维模型。综上所述点云的配准与拼接准确率将直接决定建模的精度。高精度的三维重建算法在未来5G、6G 等通信领域具有重要的作用,如采用三维重建算法可应用于5G、6G 等研究中的建模问题[4-5]。
目前国内外学者在三维重建领域已取得丰厚的成果,如Karg 等[6]通过捕获车辆第一、二矩阵边界并确定第一、第二矩形是否为同一辆车的边界,最后根据第一、二矩形和侧面方向完成对车辆的三维重建。陈佳舟等[7]针对图像点云存在噪声干扰问题,提出一种文物三维重建点云误差点的自动剔除方法,利用三维重投影方法计算三维点在图像中的可见概率并剔除噪声点,然后基于空间扩散聚类方法去除图像冗余点,完成对文物的三维重建。Rao 等[8]提出了一种基于莫尔斯理论中的3 种临界点的快速且精确的点云仿射不变特征检测和匹配方法,该方法定量评估重建模型的准确性。实验结果表明构建的三维模型精确率更高。Lan 等[9]针对前端数据关联中幸存的异常特征匹配和闭环会导致大规模点云三维重建局部最优问题,提出了一种在出现异常值时进行稳健的后端优化概率方法。该方法利用Cauchy 分布抑制离群特征匹配,以及利用Cauchy-Uniform 混合模型抑制离群闭环约束,实验结果表明在公共点云数据集上具有更好的重建效果。徐斌等[10]提出了残肢表面三维重建算法,利用深度相机扫描残肢得到点云数据,并计算该点云的特征直方图(FPFH),然后利用采样一致性初始配准(SAC-IA)和迭代最近点算法(ICP)完成残肢点云的粗配准和精配准,实现残肢表面的三维重建。张一等[11]针对传统SLAM 算法仅能重建稀疏点云等不足,提出一种特征法视觉SLAM 逆深度滤波的三维重建方法,利用视频序列影像实时、增量式地构建相对稠密的场景结构。丁忠军等[12]提出一种载人潜水器的深海地貌线结构光三维重建方法,通过改进Steger 算法,利用直接标定法求得水下地形二维空间坐标,再将获得的二维点云与多元传感器的数据进行融合,并以姿态传感器的数据矫正点云数据, 最终获得地貌的三维点云数据,最后对三维点云数据进行配准。
上述方法当点云间重叠比例较大或点云间规模大小接近时能够取得较好的三维重建效果,然而三维实体(如房子、街道等)的点云数据很难一次性采集,如果在点云数据采集过程中,激光雷达(点云采集设备)更换了位置或者角度进行连续采集时,得到的点云数据可能存在角度或大小上的变化,尤其是点云间重叠率比较低时,后续就很难进行点云的配准与拼接,从而严重影响建模精度。本文利用欧氏距离分割法和动态时间规整算法(DTW),能有效解决点云重叠率低和点云规模不一致的配准问题。
2 相关概述
点云是通过测量仪器(如激光扫描仪等)得到的实物外观表面的点数据集合,由一系列二维或三维的点组成,能够真实地反映物体表面信息。悉尼城市目标数据集[13]中的一个卡车点云如图1所示。

图1 点云示意图
要获得一辆卡车完整的点云,需要在卡车周围选择若干个位置进行数据采集,然后将采集的点云帧进行组合拼接。由于相邻位置采集的两帧点云存在部分重叠,如果找到这些重叠的点,然后对这两帧点云进行平移、旋转操作,即可完成两帧点云的拼接。点云拼接如图2 所示,图2 中使用两个激光雷达扫描长方体,激光雷达1 可以扫描到的范围为矩形RTaeh2,激光雷达2 可以扫描到的范围为矩形RTbfgc,而矩形RTbehc可以同时被两个激光雷达扫描,因此两个激光雷达扫描的点云能够覆盖长方体的正前方和右侧面,如果将两个雷达扫描得到的点云进行配准和拼接,即可完成对长方体正前方和右侧面的重建。而重建过程中最重要的就是找到这两帧点云的重叠部分,即图2 中RTbehc位置的点云,且重叠区域RTbehc的大小会影响点云拼接的效果。
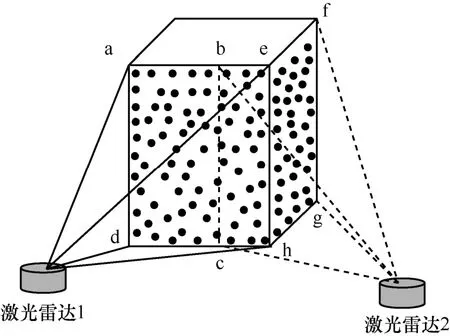
图2 点云拼接
3 点云处理
本节主要介绍如何完成两帧点云重叠区域的映射问题。首先介绍了基于欧氏距离的点云分割方法;然后提取子点云的特征值,最后考虑不同位置获取的点云规模不一致,采用DTW 算法完成子点云的映射。为降低点云映射的计算复杂度,将不同激光雷达采集的点云映射到二维平面上,点云二维平面映射过程如图3 所示,以两个激光雷达的水平中垂线为基准,距离h处构建二维投影平面XOY。将两个激光雷达扫描得到的点云同时映射到二维平面上,以映射后的二维点云为拼接的基础,完成重叠点云“关键位置”的所搜和匹配。
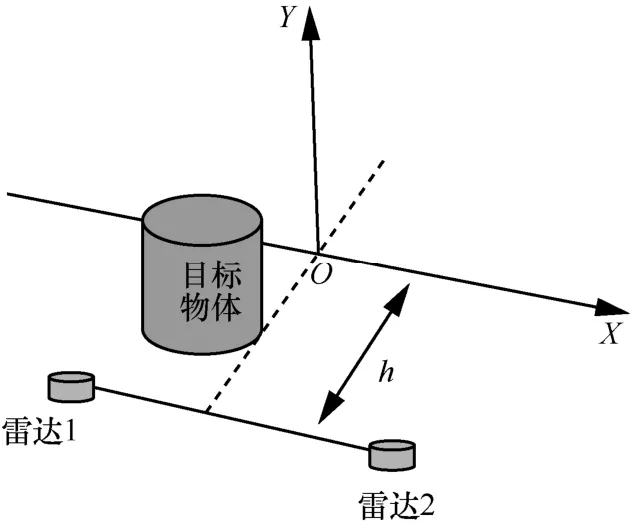
图3 点云二维平面映射
3.1 点云分割
如果不对大面积的点云进行分割,则无法有针对性地寻找到两帧点云的重叠区域。为有效地对点云进行划分,采用基于欧氏距离的点云分割算法,该方法逐步扫描点云内的点,如果当前扫描点与聚类种子点之间的距离d小于设定的阈值D,则将当前扫描点聚类到该种子点所属的类中;否则将当前扫描点设置为新的聚类种子,根据预设阈值D判断下一个扫描点是否与新的种子点属于同一类。重复以上步骤,直到所有的点都被聚到不同的类中。通过聚类,可以减少物体边界点对特征点检测的影响,同时,对于点云中不规则的离散点,往往其所在类的尺寸较小,很容易将其滤掉。点云分割流程方法见算法1,每个队列表示分割得到的一个子点云,最终求取子点云的平均规模(即子点云内平均包含点的数量),并将子点云规模小于平均规模的子点云滤除。
算法1基于欧氏距离的点云分割算法
输入待分割的点云O
输出分割后的子点云Qm
(1)设置多个队列Qm(m表示队列数量),预设欧氏距离阈值D;
(2)i=1;
(3)随机搜索点云O中某个点pi作为聚类种子点,即C=pi;

(7)i=i+1;
(8)判断点云中的点是否都加入相关队列,如果是,结束算法,如果否,则返回步骤4。
3.2 子点云特征提取
由于激光雷达扫描物体时,物体不同表面产生的点的数量、密度和组合都是不同的,每个位置产生的点云总体上是有区别的,由于不同点云中点分布存在差异,本文假设满足二维正态分布,且概率密度函数能够很好地描述点云中点分布的密度、位置等差异,因此采用二维正态分布的概率密度值作为点云的特征,该特征值较传统的均值、方差等指标具有更强的描述性。为后续进行点云的配准和拼接,需找到具有部分重叠的两帧点云高度重合的位置(关键位置),反映在物体上,即不同位置的激光雷达扫描物体相同区域得到的点云。根据第2.1 节的点云分割方法,将两帧具有重叠的点云进行分割,然后将两帧点云分割后的子点云进行特征匹配,寻找到两帧点云的“关键位置”。本节介绍一种子点云的特征提取方法,特征提取原理如图4 所示,首先求取该子点云的重心重心坐标如式(1)所示。然后以子点云的重心为中心构建等距离g(unit)同心圆,直到最大的一个同心圆将该点云中所有的点全部囊括在内,其中,1(unit)表示20 个像素。
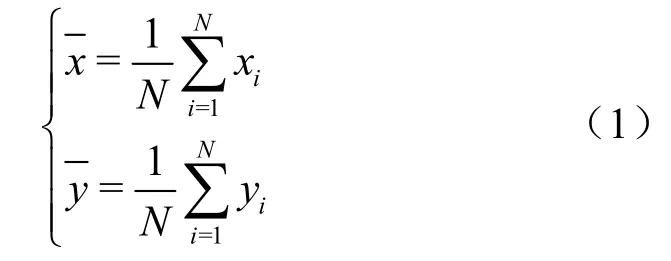
其中,xi、yi分别表示点的横纵坐标,N表示子点云中点的数量。
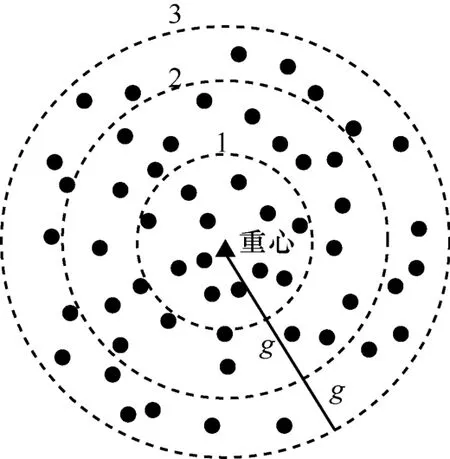
图4 特征提取原理
假设子点云内部的点服从二维正态分布,即将每个点的坐标(xi,yi)看作二维随机变量,那么子点云的概率密度函数如式(2)所示。

其中,μ1、μ2为x和y的均值,见式(1),σ1和σ2为x和y的方差,ρ为x和y的相关系数,绝对值小于1。
为了提高子点云的匹配准确性,使用二维正态分布模型的概率密度均值来表示子点云的特征。根据概率密度函数f(x,y)可求得点云中每个点的概率密度,求取目标范围内所有点的概率密度值之后计算该目标范围内点云的平均概率密度值,如式(3)所示,以平均概率密度值作为子点云的一个特征。
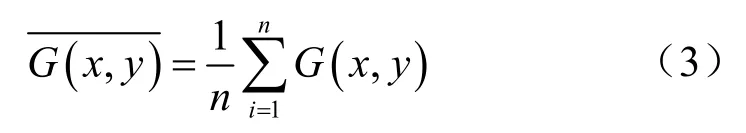
其中,G(x,y)表示点(x,y)位置的概率密度值,n表示目标范围内点的数量。

其中,k表示点云划分时同心圆区域的数量。
3.3 子点云映射
根据第2.1 和2.2 节的方法可以将激光雷达扫描得到的原始点云分割为若干子点云,然后求得子点云的特征序列。在进行两帧原始点云匹配时,主要是根据特征序列实现两帧原始点云中某些相似度较高的子点云映射。
激光扫描可类比拍照,当照相机位于不同位置拍摄同一个物体时,照片的大小也是有区别的。相同原理,激光雷达位于不同位置扫描同一个物体时,其得到物体表面的点云也存在大小的区分,本文称为点云规模的大小不同。如果待拼接的两帧点云存在规模上的差别,则得到的子点云特征序列长度也是不同的,不同规模子点云划分如图5所示,子点云p与子点云q形状非常接近,点的分布也非常接近,但因为激光雷达所处的位置不同,导致点云规模存在差别,理论上这两块子点云是激光雷达位于不同位置扫描三维物体同一区域得到的数据。由于点云规模不同,而点云划分的同心圆之间的距离相同且都为g,最终得到的子点云特征序列长度也存在差别,如子点云p的特征序列Fk长度为3,而子点云q的特征序列长度为5。针对这种情况,传统的点云配准方法很难解决该问题。
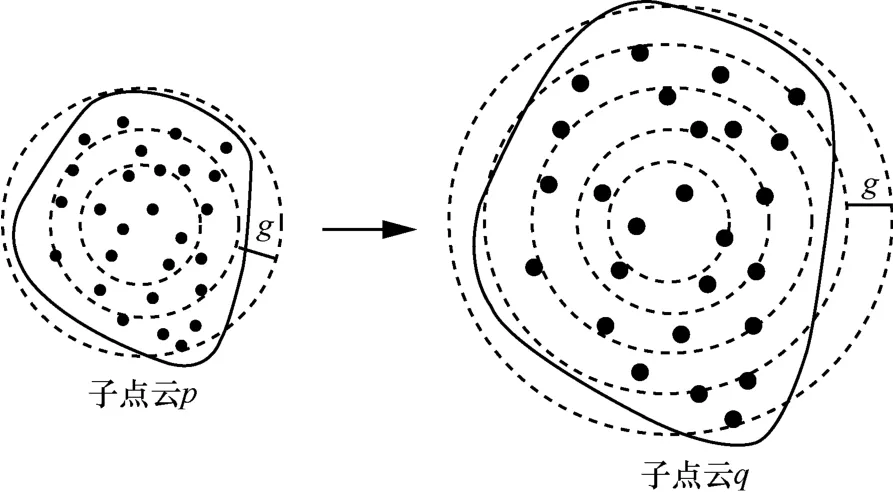
图5 不同规模子点云划分
为解决点云规模不一致的拼接问题,提出一种基于动态时间规划(DTW)的点云特征序列匹配方法[14-15]。DTW 通过将特征序列进行延伸和缩短,计算两个特征序列性之间的相似性。假设子点云p和子点云q的特征序列分别如式(5)、式(6)所示。
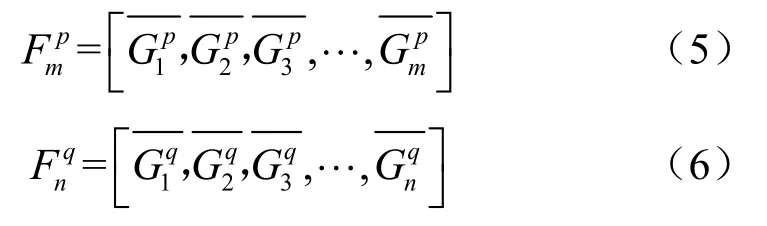
其中,m表示子点云p的特征序列长度,n表示子点云q的特征序列长度。
当m=n时,则可以采用特征序列之间的欧氏距离衡量两帧子点云特征序列的相似性,而当m≠n时,需要将其中一个特征序列进行线性缩/放对齐,使得两组特征序列的长度相同,才可以进行相似性衡量。但线性缩放没有考虑特征序列各个阶段在不同情况下的长度变化,识别效果不可能最佳,更多地采用动态规划(2ynamic programming)的方法。DTW 序列对齐原理如图6所示,利用两组特征序列构建一个网格矩阵,矩阵中每个元素di,j表示特征序列qnF的第i个元素与特征序列第j个元素之间的欧氏距离,每一个矩阵元素对应的下标(i,j)就表示两组特征序列的对齐点。

图6 DTW 序列对齐原理
从初始点d1,1到结束点d5,3有较多条路径,且路径的数量随着矩阵规模呈指数增长,如何找到一条路径使得代价最小,最小代价的一条路径即为两组特征序列的最佳对齐点,最小代价函数如式(7)所示。

基于上述方法对两组特征序列进行对齐,特征序列上的点能够找到最佳对齐点,DTW 序列对齐原理如图7 所示。根据对齐后的两组特征序列之间的欧氏距离作为相似度,如式(8)所示。
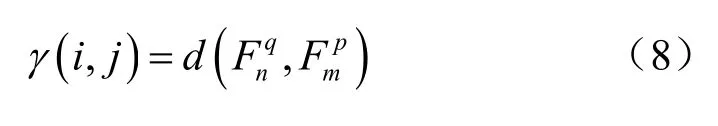
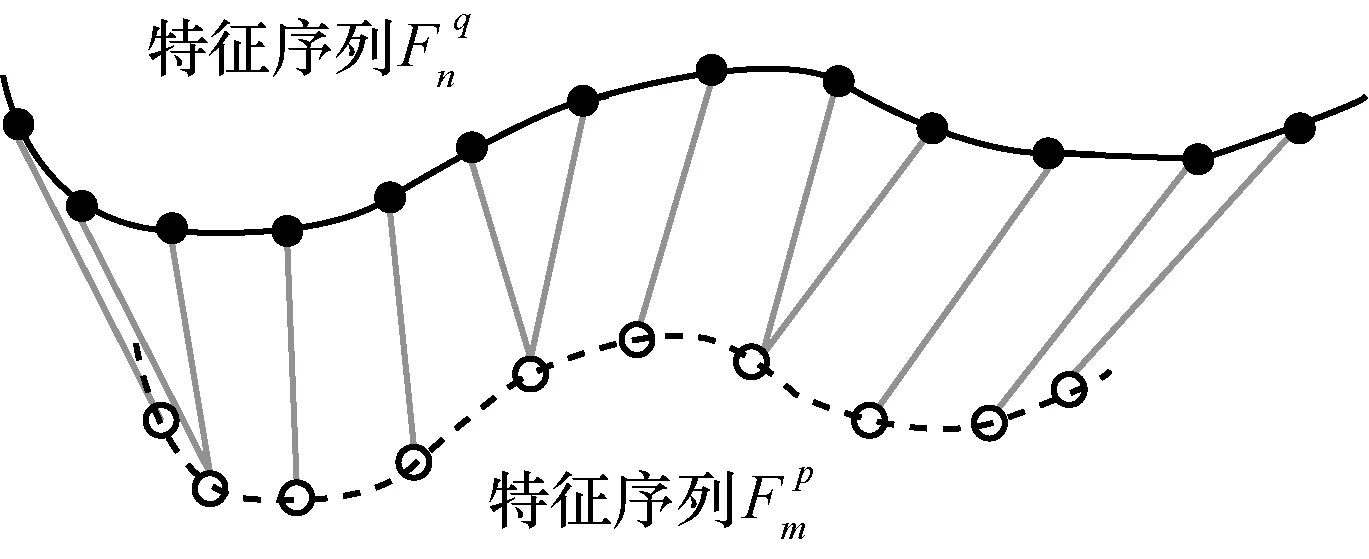
图7 DTW 序列匹配
利用原始点云的分割、特征提取和子点云映射方法即可寻找到两块原始点云中相似性较高的位置,以这些位置为基准进行点云的配准将能够有效地解决两帧点云重叠率低以及点云规模不统一问题。本文利用上述点云映射方法所搜到两帧原始点云中相似性最高的子点云完成映射。
4 点云配准
对两帧点云P和Q进行分割,并获得了互相映射的子点云p和q,然后基于子点云p、q采用ICP 算法进行配准,由于ICP 算法对点云的初始位置有较高的要求,这里需要采用SAC-IA[16-17]算法先对点云粗配准,因此要配准的两帧点云具有较好的初始位置,再利用ICP[18-19]算法进行精配准,如式(9)所示。

其中,R、t分别表示旋转和平移矩阵,由SAC-IA算法和ICP 算法得到,e为优化误差。求得的R和t再对P和Q进行配准,即可完成拼接。由于SAC-IA 算法和ICP 算法已经非常成熟,本文不再做过多的介绍。点云配准算法见算法2。
算法2原始点云配准算法
输入点云P和Q。
输出旋转矩阵R,平移矩阵t。
(1)对点云P和Q分割,得到子集pi和qi;
(2)对子集分别求取二维正态分布的概率密度均值;
(3)基于DTW 算法完成子点云的映射;
(4)配准匹配的子集并获得旋转矩阵R,平移矩阵t,作用于P和Q;
(5)完成原始点云P和Q的配准与拼接。
算法2 介绍了点云配准算法的总体流程,该算法基于SAC-IA 算法和ICP 算法实现点云的粗配准和精配准。SAC-IA 算法与ICP 算法的总体实践复杂度为O(sk2),其中,s表示点云中点的数量,k表示点云被均分的份数,该值与变量g相关。而DTW 算法的实践复杂度为O(mn),其中,n和m分别表示两帧点云特征向量的模。综上所述,本文算法的总体复杂度为O(sk2)+O(mn)。
5 实验分析
5.1 点云重叠率对配准影响
传统的ICP 算法主要解决大规模重叠点云的配准与拼接问题,而当点云规模较小时,很难取得好的拼接效果。本文主要研究当两帧点云具有较低重叠率和点云规模不同时的配准拼接问题。实验采用ASL Datasets 中的“牛”点云作为实验对象,将该点云按一定比例重叠区域进行分割,然后验证本文提出的方法在不同重叠率情况下的配准与拼接效果,实验中点云的欧氏距离分割阈值D=15,点云划分同心圆之间的间隔g=3。分割示意图如图8 所示。

图8 分割示意图
首先固定一个旋转矩阵Ri和平移矩阵ti,分别如式(10)、式(11)所示,将这两个矩阵作用于图8 中分割后的“牛”下部分的点云,使得两帧点云在位置上错开。两帧点云位置错开后,利用本文提出的点云配准方法(partial overlapping point clou2 registration metho2 base2 on 2ynamic feature matching,PPCR)和ICP 算法分别对两帧点云进行配准,求取PPCR 和ICP 算法生成的旋转矩阵Rj和平移矩阵tj,再与固定的旋转矩阵Ri和平移矩阵ti进行对比,计算旋转误差和平移误差,分别如式(12)和式(13)所示。

PPCR 算法的实验结果如图9 所示,表明随着点云之间重叠率的降低,两帧点云的拼接时的旋转误差ER和平移误差Et都呈指数升高,因为重叠率越小,所以拼接算法能找到两帧点云相似的区域的可靠性越差,导致拼接误差较大。
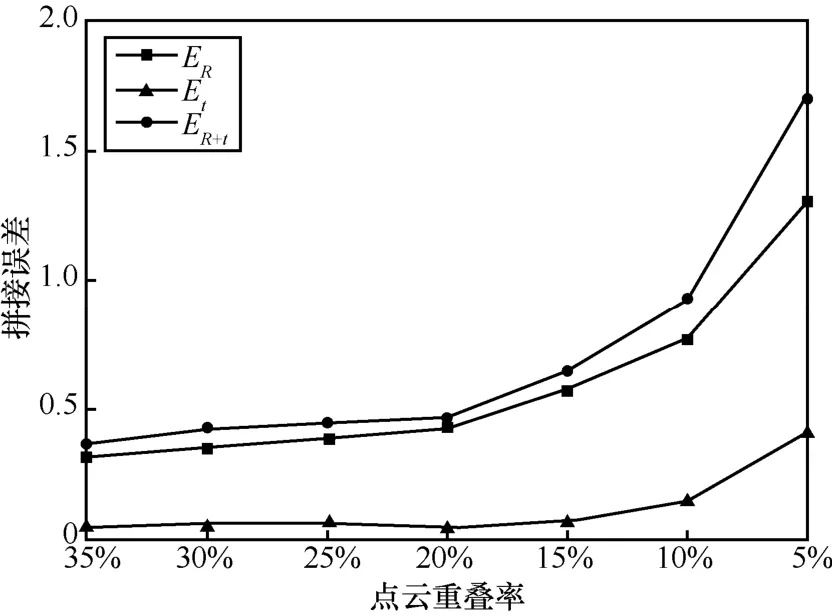
图9 点云重叠率对PPCR 拼接效果影响
PPCR 算法与ICP 算法的对比结果如图10 所示,ICP 在点云重叠率高于20%时有效,否则无法完成点云的拼接,且ICP 算法的拼接误差大于本文提出的PPCR 算法,因为ICP 算法并未考虑点云重叠率时的拼接问题,其主要针对大面积重叠的点云之间的拼接,而PPCR 算法利用欧氏距离分割,提取了重叠部分点云的特征,且采用了DTW 曲线相似度动态匹配算法,即使在重叠率较低时也能够准确地找到点云间的重叠区域,最后根据重叠区域进行拼接,因此拼接误差较ICP 算法更低。

图10 PPCR 与ICP 拼接误差对比
单独采用ICP 算法进行点云配准存在收敛速度慢、配准误差大等问题。本文先采用SAC-IA算法实现点云的粗匹配,将位置错开的点云快速实现合拢,然后采用ICP 算法进行精匹配,理论上能够降低点云配准的时间。本实验验证当点云不同重叠率下,ICP 算法和PPCR 算法的配准时间,结果见表1。

表1 时间复杂度分析(时间/s)
实验结果表明,PPCR 算法在所有重叠率下的配准时间都低于ICP 算法,因为PPCR 算法先采用SAC-IA 算法快速将两帧位置偏差较大的点云快速的匹配并合拢,然后采用ICP 算法进行精匹配,其中,SAC-IA 算法的效率较高。而ICP 算法在处理两帧点云偏差较大情况时,收敛速度非常慢,因此导致配准过程所需时间较长。
5.2 噪音对点云配准影响
激光雷达发出的微波在真实环境中容易产生衍射、折射等现象,会导致采集的点云数据包含噪音,由于噪音的随机性会影响点云配准过程中的子点云映射,因此消除噪音有利于提高点云配准的准确率。噪音在点云中一般是以少量离散点的形式存在,而本文提出的PPCR 算法在点云分割阶段将点云进行聚类,因此可以根据聚类中包含点的数量来滤除噪音,当类规模小于一定值时删除该类,滤噪对比如图11 所示,当基于欧氏距离的点云分割得到的子点云所包含的点数量小于子点云平均包含的点数量的一半时,则删除该子点云,实验中点云的欧氏距离分割阈值D=15。利用第4.1 节的方法将点云分为两部分,重叠率为20%,验证不同程度的滤波情况下PPCR 算法拼接点云的误差,实验结果见表2,表2 中拼接效果一栏表示两帧点云拼接是否有效,为1 表示有效,为0 表示无效。S 为原始点云经欧氏距离分割后得到若干子点云后,子点云平均包含点的数量,如式(14)所示。

图11 滤噪对比

其中,n表示子点云的总数量,si表示点云i中包含点的数量。
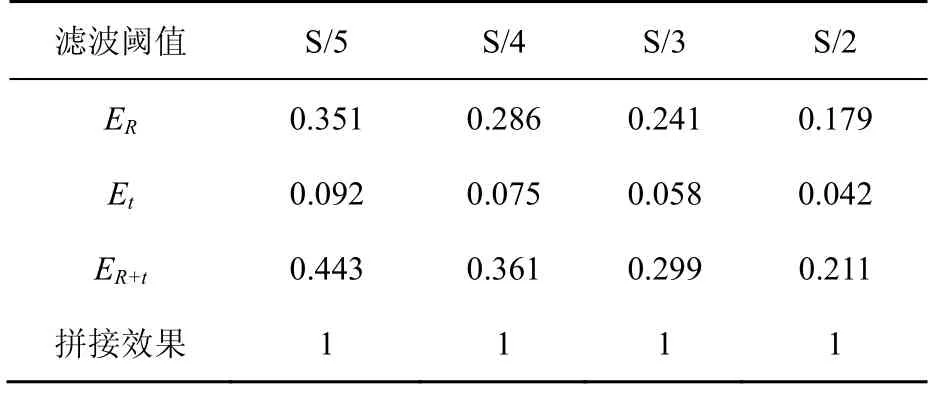
表2 滤波对点云拼接的影响
实验中将小于滤波阈值的子点云删除,结果见表2,随着滤波阈值的增加,PPCR 算法的点云拼接误差逐渐减小,总体误差ER+t一直维持在0.5以下,因为滤波阈值越大,能够滤除的噪声越多,所以待拼接的两帧子点云之间的映射更准确。
5.3 点云规模差异对子点云映射影响
PPCR 点云配准与拼接算法采用动态时间规则方法进行点云特征序列匹配,理论上能够有效解决待拼接的两帧点云规模不一致的映射问题。如果能够准确地映射两帧原始点云中相似性极高的子点云,则后续可以根据该子点云进行原始点云的拼接。以“兔子”点云为实验对象,不同规模点云如图12所示,为构建不同规模点云,对原始点云进行下采样,使得下采样后得到的点云与原始点云保持相同的结构,但点的数量不同,然后将下采样后的点云缩小到原始点云的1/2,实验中下采样矩阵见表3。初始时刻两帧点云处于相互完全重叠位置,然后利用已知的旋转矩阵和平移矩阵作用于其中一个点云,使得两帧点云位置错开(见第4.1 节的旋转与平移),以第4.1 节的配准误差方法衡量两帧点云的配准精度,实验结果见表3,表3 中配准效果一栏表示两帧点云配准是否有效,为1 表示有效,为0表示无效。实验中的下采样方法为仅采集采样矩阵中心位置的元素替代原采样矩阵中所有值。
实验结果表明随着下采样矩阵的增加,配准误差会升高,下采样矩阵为3×3 时,配准误差较小,仅为0.324,而下采样矩阵为9×9 时,点云拼接误差较大为0.979。因为下采样矩阵越大,下采样后得到的点云越稀疏,损失的特征越多,所以配准误差也就越高。但利用激光雷达处于不同位置扫描同一个三维实体时,其得到的点云之间的差距不可能达到3×3 下采样这种损失,且实验误差表明即使对原始点云进行下采样操作,在丢失大部分数据时,两帧点云的配准仍具有较高的稳健性,因此本文提出的利用DTW 算法进行子点云特征序列的匹配方法能够有效地应对点云规模不同而导致拼接效果差的问题。

图12 不同规模点云
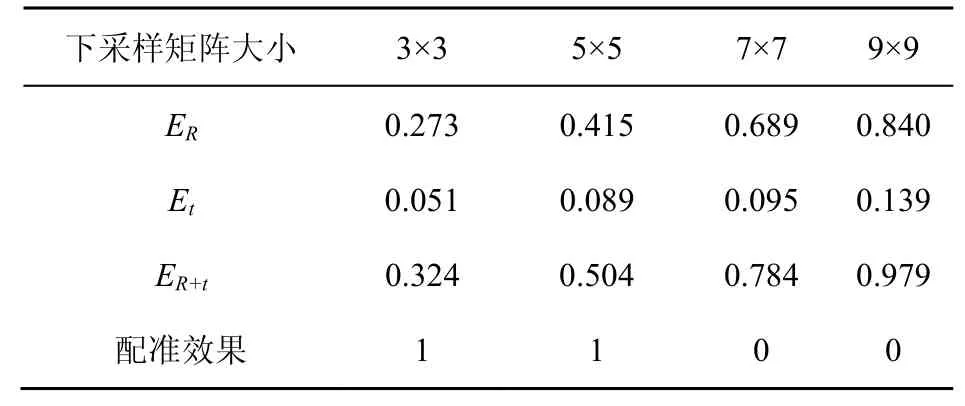
表3 不同规模点云配准误差
5.4 分割距离g 与收敛性分析
在第2.2 节子点云特征提取阶段提出采用变量g将点云进行均匀分割。当g的取值不同时,会得到长度不同的特征向量,这会影响点云的拼接效果。为验证g在不同取值时的点云拼接误差,实验设定g的取值为2~10,其中两帧点云的重叠率为20%,实验结果见表4。
实验结果表明随着g的增加,点云拼接的总体误差ER+t首先呈降低趋势,因为g增加,提取同一帧点云的特征增加,从而降低了总体误差。当g大于5 时,总体误差基本呈平稳波动趋势,因为此时点云被划分的足够精细,特征提取的比较全面。但g的取值并非越大越好,同时还要考虑算法的复杂度。

表4 变量g 对点云拼接的影响
6 结束语
针对目前点云配准与拼接方法较难解决部分重叠、规模不一致的点云配准与拼接问题,提出一种动态特征匹配的部分重叠点云配准方法,利用点之间的欧氏距离进行子点云的分割,然后以二维正态分布模型提取子点云的特征序列并利用DTW 算法完成特征序列的相似性匹配,接着将相似度最高的子点云进行映射,最后利用SAC-IA算法和ICP 算法完成点云的配准与拼接。实验结果表明该方法在点云低重叠率和点云规模不一致情况下均能以较小的误差完成配准和拼接。

