基于混合高斯变分自编码网络的异常检测算法

陈华华，陈哲，郭春生，应娜，叶学义，章坚武

（杭州电子科技大学通信工程学院，浙江 杭州 310018）

1 引言

异常检测是指在数据中检测出不符合期望行为的数据。异常数据在统计领域也被称为偏差值或离群值，是指远离大量正常数据点的数据[1]。异常产生的原因有很多，比如数据本身的错误，或人为因素，而这些异常往往蕴含着一些隐秘的行为信息。在金融尤其是互联网金融领域[2]，高效准确的异常检测系统能够识别并预警用户潜在的异常行为，控制金融风险，减少金融欺诈行为导致的经济损失。因此，如何从海量数据中监控并检测异常数据是一个亟待解决的重要问题。此外，异常检测还广泛应用于网络入侵检测[3]、医疗图像辅助病症判断[4]、工业设备异常监控[5]、智能安防监控[6]等领域，为各类系统的正常运转提供重要支撑。

2 相关工作

LOF（local outlier factor，局部异常因子）算法[7]是一种经典的基于密度估计的异常检测算法，其将数据点的可达距离、局部可达密度与其邻域数据点进行比较，并计算局部异常因子评估数据的异常程度，判断数据是否属于异常。基于密度的异常检测算法适合用于数据分布不均的情况，算法复杂度较高。Liu 等[8]提出了孤立森林（isolation forest，IF）算法，其采用集成学习的方式，利用二叉搜索树对样本进行孤立计算，并以此衡量样本的异常程度，异常点往往因为具有与正常点分离的特性而被更快地孤立，但是该方法难以检测局部异常的情况。

近年来，随着数据维度的提高，深度神经网络已经显示出其优于传统机器学习的优点。An 等[9]提出了使用变分自编码器进行异常检测，并提出使用重构概率衡量分布差异程度，该方法优于使用自动编码器的方法。杜辰飞等[10]提出了一个基于稀疏自编码器的异常检测模型，输入正常数据对稀疏自编码器进行训练和优化，然后基于测试数据的重构误差检测数据中的异常情况。Li 等[11]提出了基于胶囊网络的深度异常检测算法，其使用胶囊网络搭建编码器和分类器，并基于预测概率和重建误差对图片数据进行异常检测。丁建立等[12]采用自然语言处理常用的seq2seq 模型对数据进行建模，利用数据的重构误差对数据进行异常检测。

目前的异常检测算法大多依赖于重建误差或重建概率等启发式方法进行异常判断，没有利用数据的特征表示进行异常判断。因此，本文以混合高斯先验建立自编码器，以得到数据更合理的特征分布，然后以自编码器构建深度支持向量网络压缩特征空间，通过寻找最小超球体分离异常数据和正常数据，从而实现对异常数据的检测。该方法摆脱了目前主流的基于重构误差或重建概率的异常检测方法，基于数据特征的优化进行异常检测。

3 异常检测模型

3.1 混合高斯变分自编码器

变分自编码器[13]通过将深度学习与概率统计相结合，能够学习到数据的特征分布。标准的变分自编码器的优化目标如式（1）所示。

模型通过最小化近似后验分布和假设先验分布之间的 KL 散度，使优化目标证据下限（ELBO）最大化。然而，标准变分自编码器中先验采用简单的标准正态分布，可能会导致后验塌陷问题[14]，并且容易忽略一些潜在的变量约束，导致无法较好地逼近不同类别数据的分布，影响编码和解码的效果。为此本文引入混合高斯分布作为变分自编码器的先验分布，如式（2）所示。

此时，式（1）中的第一项为混合高斯分布的KL 散度。式（2）、式（3）的高斯分量个数相同，都为M。一般地，先验分布的混合高斯个数应不同于后验分布的混合高斯个数，这样先验和后验中的高斯分量之间就必须进行逐一匹配，但是会出现后验中多个高斯分量匹配先验分布中某个高斯分量的情况，而后验分布中的这些高斯分量的均值和方差都是由网络从各批训练数据中取得的，训练数据的切分会影响均值和方差的估计，同时高斯分量个数的选择也会影响匹配的准确性，导致求解问题复杂化。为简化问题求解，本文采用了先验和后验由相同个数的高斯分量组成。但是到目前为止，尚未有一个高效的算法能够求出与混合高斯分布相关的KL 散度的解析解。为了解决这个问题，Hershey[15]提出了混合高斯分布之间的KL 散度的近似求解算法，该算法使用变分推断求解出所需要计算的KL 散度的上界。因此可以将最小化KL 散度的目标转换为最小化其近似上界。

根据Hershey 提出的近似算法，可以得到式（1）中的第一项KL 散度的表达式，如式（4）所示。

3.2 深度支持向量网络

支持向量数据描述（support vector 2ata 2escription，SVDD）是Tax 等[16]提出的一种在统计学理论基础上发展的单值分类方法。SVDD 的目标是在特征空间Fk中找到中心c∈Fk、半径R>0的超球体，该超球体将大多数目标类数据包围，以此分离目标类数据与所有非目标类数据。

假设输入数据为x(i)，i=1, …,N，SVDD 在特征空间上寻找最优超球体的优化目标被定义为式（7）。

本文训练一个混合高斯变分自编码网络，将网络输出拟合到最小超球体中，以学习数据特征分布变化的共同因素。本文将深度支持向量网络的目标函数定义为式（8）：

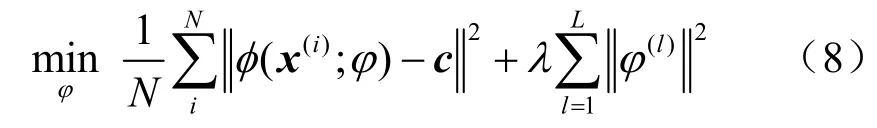
其中，φ是自编码网络的参数，φ(x(i);φ)是自编码网络输入为x(i)时的输出，第二项是L2 正则化项，L是神经网络的层数，φ(l)是自编码网络第l层的参数，λ是正则化系数，该正则化项可以减少模型过拟合，提高模型的泛化能力。由此，将数据的特征被压缩到了以c为中心的超球体内。

对于给定的测试数据x′，计算测试数据经自编码网络的输出到超球体中心的距离，定义深度支持向量网络的异常分数s(x′)如式（9）所示。

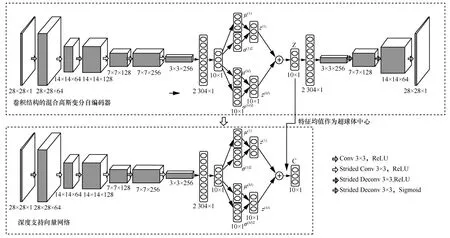
图1 异常检测模型网络结构

3.3 网络模型

本文使用卷积神经网络搭建混合高斯变分自编码器，其网络结构如图1 所示。在编码器中，输入图像首先经过一层含64 个卷积核、大小为3×3、步长为1 的卷积层，激活函数使用非线性的ReLU 函数。池化层在进行下采样操作的时候，存在丢失有价值的信息的问题[17]。因此本文使用含64 个卷积核、大小为3×3、步长为2 的卷积层代替池化层进行下采样，保留图像中的重要信息。然后级联一层含128 个卷积核、大小为3×3、步长为1 的卷积层，使用含128 个卷积核、大小为3×3、步长为2 的卷积层代替池化层。最后级联含256 个卷积核、大小为3×3、步长为1 以及含256 个卷积核、大小为3×3、步长为2 的卷积层，然后级联一个reshape 层，将数据维度转换为2 304×1，再连接一个维数是10 的全连接层。

解码器中使用反卷积完成对特征的复原工作。解码器在结构上和编码器对称，使用两个维数分别是10 和2 304 的全连接层，再级联一个reshape 层，将数据维度转换为3×3×256，再级联3 层反卷积层，分别具有128 个、64 个、1 个大小为3×3 的卷积核。与编码器类似，解码器使用步长为2 的反卷积层代替上采样。除最后一层反卷积使用Sigmoi2 作为激活函数，其余卷积层、反卷积层均使用ReLU 作为激活函数。

训练得到的混合高斯变分自编码器的编码器部分作为深度支持向量网络，并以学习获得的编码器参数作为初始值，以特征均值作为超球体中心，进一步训练深度支持向量网络。

3.4 异常检测

在训练阶段中构建并训练混合高斯变分自编码器，通过训练混合高斯变分自编码器得到正常类别数据的特征表示及特征的均值c。然后将均值c作为超球体中心，构建并训练深度支持向量网络。在测试阶段中将测试数据输入深度支持向量网络，根据式（9）计算异常分数。异常检测的判别如式（10）所示，当测试数据的异常分数小于阈值时，则说明该数据落在超球体之内，认为是正常数据；当测试数据的异常分数大于阈值时，则说明该数据落在超球体之外，认为是异常数据。

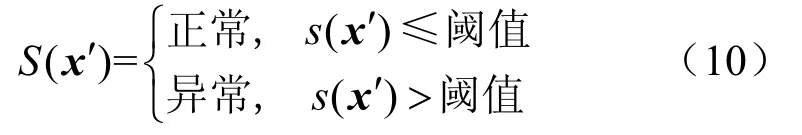
4 实验结果分析

4.1 实验配置及数据集

实验采用Win2ows 10 平台下的Python 3.6 编译器。计算机参数配置为Intel Core i5-7300HQ@2.50 GHz CPU，内存为8 GB，使用的编程环境为TensorFlow 和Keras，编程语言为Python。网络使用正态分布随机值初始化网络参数，batch size 设置为100，使用A2am 优化器更新模型参数，学习率设置为0.000 1。异常检测就是在数据中检测出远离大量正常数据点的数据，将正常数据看作目标类数据，将各种异常数据均看作离群类数据，因此在这个意义上可以看作一个二分类问题；同时Tucker[18]也指出，在混合高斯分布中，由两个高斯分布分量组成的混合高斯分布具有较好的描述性质，并且兼顾了参数个数和拟合效果，保证了模型的灵活性。因此本文中混合高斯自编码器的先验和后验均使用二分量的混合高斯分布，其系数分别为coefficient、1−coefficient。

为评估本文方法的有效性，本文采用了MNIST 数据集[19]和Fashion-MNIST 数据集[20]用于实验测评。MNIST 数据集是一个包含 10 种不同数字（0～9）的数据集，将其中1 个数字作为正常类别数据，其余9 个数字作为异常类别数据。Fashion-MNIST 数据集是一个包含10 种不同时尚商品的数据集，将其中1 种时尚商品作为正常类别数据，其余9 种时尚商品作为异常类别数据。两个数据集均以正常类别的数据作为训练数据，约各有6 000 个样本。两个数据集的测试集中各有10 000 个样本，其中包括正常类别数据和异常类别数据。实验中本文将两个数据集中的图像像素值归一化到[0,1]。

4.2 评价标准

本文使用异常检测模型常用的AUC（area un2er curve）指标进行评估。AUC 值一般用于评价二分类模型，其值是ROC（receiver operating characteristic）曲线下的面积，常由混淆矩阵得到，混淆矩阵见表1。其中，TP（true positive）表示实际和预测均为正常的样例；FN（false negative）表示预测为异常的正常样例；FP（false positive）表示预测为正常的异常样例；TN（true negative）表示实际与预测均为异常的样例。

表1 二分类的混淆矩阵

由此可根据式（11）、式（12）计算出假阳性率（false positive rate，FPR）和真阳性率（true positive rate，TPR）。将式（9）中异常分数s(x′) 转换成概率，则式（10）中阈值的取值落在[0,1]，在[0,1]等间隔取200 个阈值，每一个阈值根据式（11）和式（12）得到一组FPR 和TPR 值。根据设定阈值的不同，从模型中得到各组 FPR和TPR 值，以FPR 作为横坐标，TPR 作为纵坐标，即可得到模型的ROC 曲线。由于异常检测中样本往往存在分布不均的情况，使用准确率指标评估模型并不合适，而采用ROC 曲线下的面积AUC 指标同时考虑了模型针对正常例和异常例的分类能力，因此适合作为异常检测模型的评估指标。

4.3 MNIST 数据集实验结果

本文在MNIST 数据集上进行了异常检测实验。根据高斯分量混合系数的不同会产生多种混合高斯先验，为了得到最佳的混合高斯分布的混合系数（coefficient），本文分别依次以10 个不同数字为正常数据，其余数字为异常数据，coefficient 在[0.1,0.9]以0.1 为步长取值，计算AUC 值，每个coefficient 值求取10 个不同数字的平均AUC 值，画出平均AUC 值和coefficient值之间的曲线关系，结果如图2 所示。由图2 可知，本文算法在MNIST 数据集上的最佳混合高斯系数为（0.5，0.5）。

本文也与其他异常检测算法进行了比较，实验结果对比见表2，最优结果加粗显示。

表2 中数字“4”的AUC 略低于最高值，主要是因为类似于、、的数字“9”检测为数字“4”，这对混淆矩阵中的FP 值影响比较大；数字“7”的AUC 略低，主要是因为不能检测出类似于的数字“7”，这对FN 值影响比较大。从表2 可知，本文算法的平均AUC 值较其他异常检测算法有一定的提高，表明本文算法在MNIST 数据集中实现了较好的检测效果，能够进行有效的异常检测。

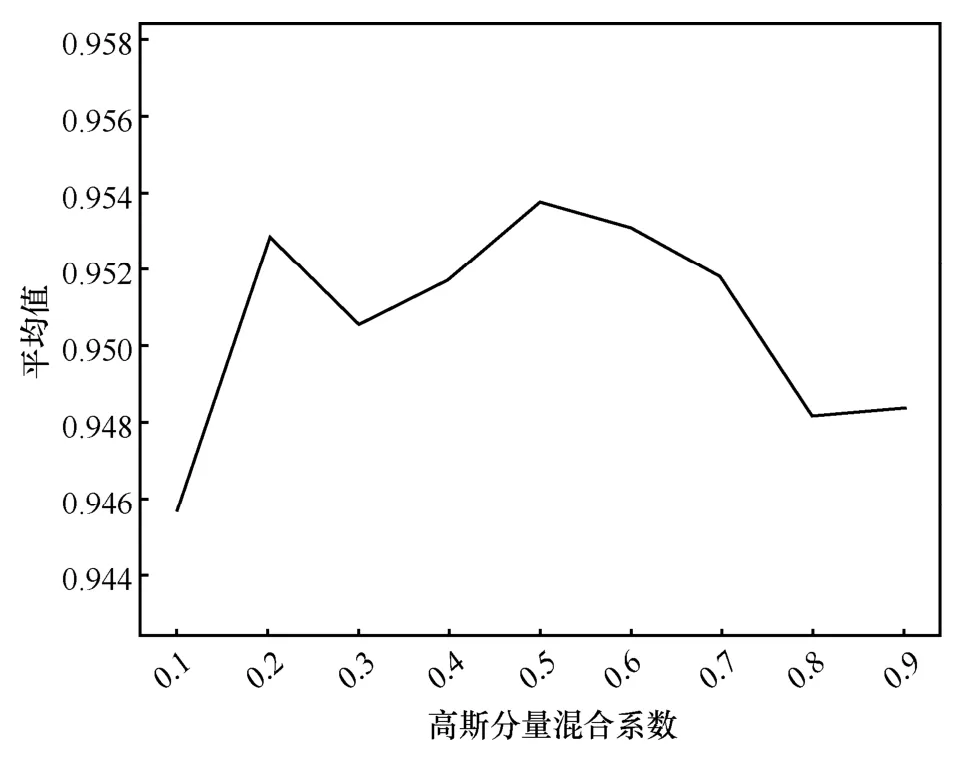
图2 MNIST 数据集在不同高斯分量混合系数下的实验结果平均值

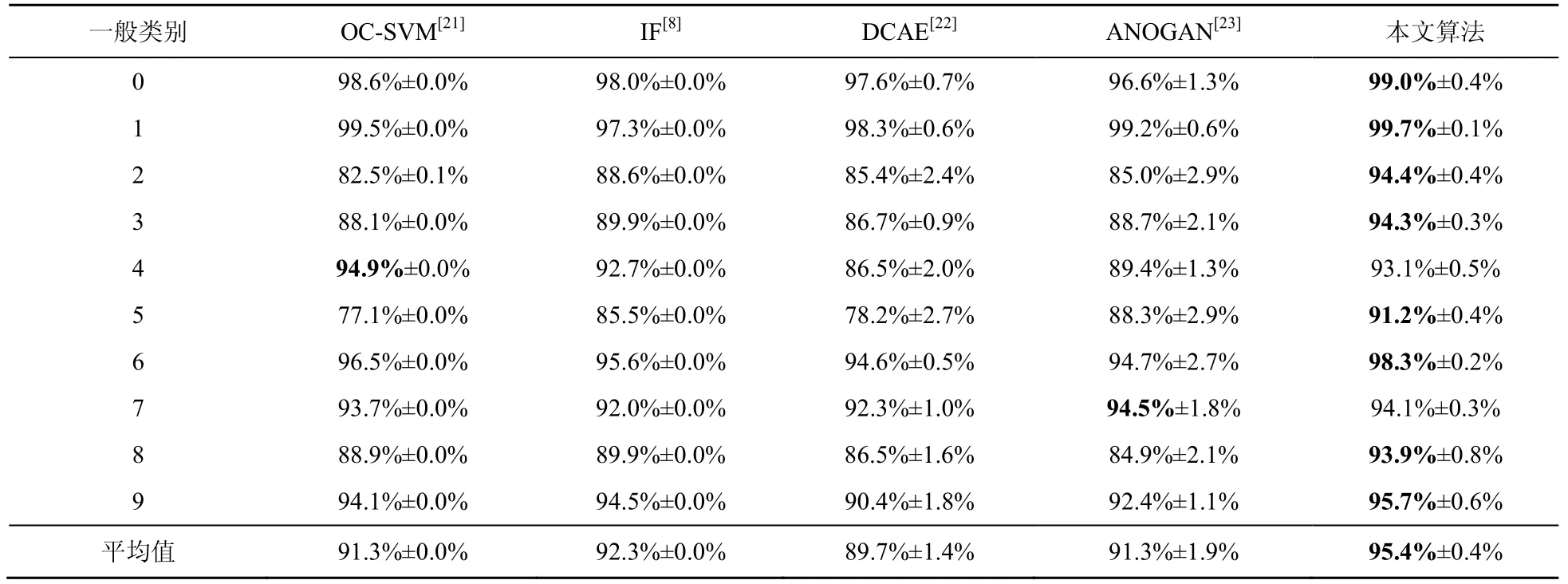
表2 MNIST 数据集在各种异常检测方法下的实验结果对比

4.4 Fashion-MNIST 数据集实验结果

本文也在Fashion-MNIST 数据集上进行了异常检测实验。为了得到混合高斯分布的最佳混合系数，本文分别依次以10种不同商品为正常数据，其余商品为异常数据，coefficient 采用和MNIST 数据集类似的方法，求得每个coefficient 值时10 种不同商品的平均AUC 值，画出平均AUC 值和coefficient 值之间的曲线关系，结果如图3 所示。由图3 可知，本文算法在Fashion-MNIST 数据集上的最佳混合高斯系数为（0.4，0.6）。

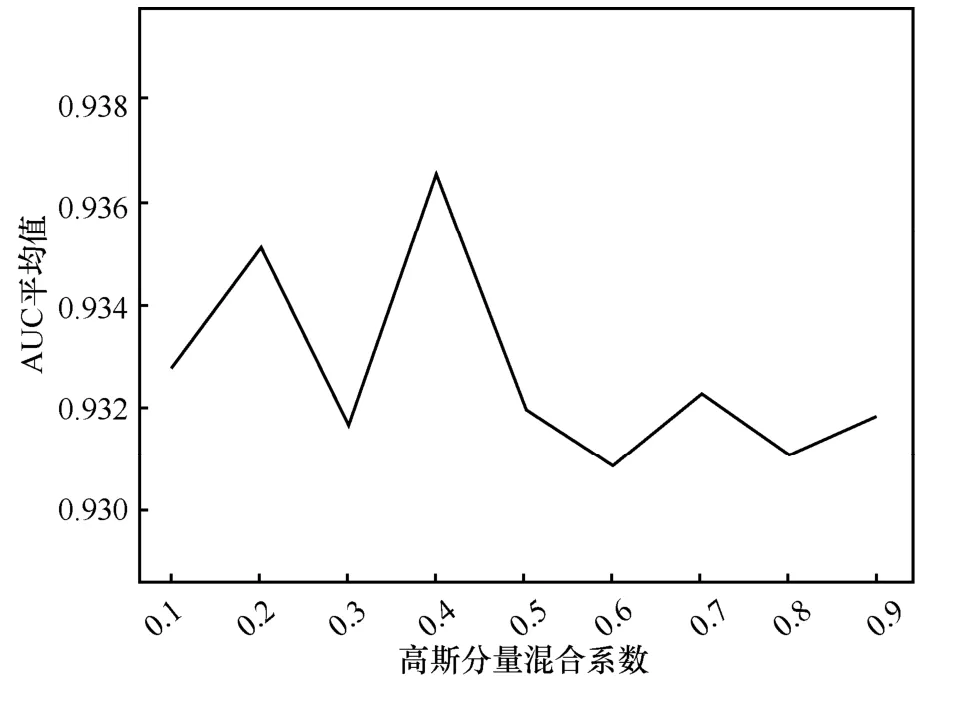
图3 Fashion-MNIST 数据集在不同高斯分量混合系数下的实验结果平均值

同样，本文也与其他异常检测算法进行了比较，实验结果对比见表3，最优结果加粗显示。

由表2 和表3 可知，本文算法具有较好的异常检测效果，并优于当前的一些异常检测算法。

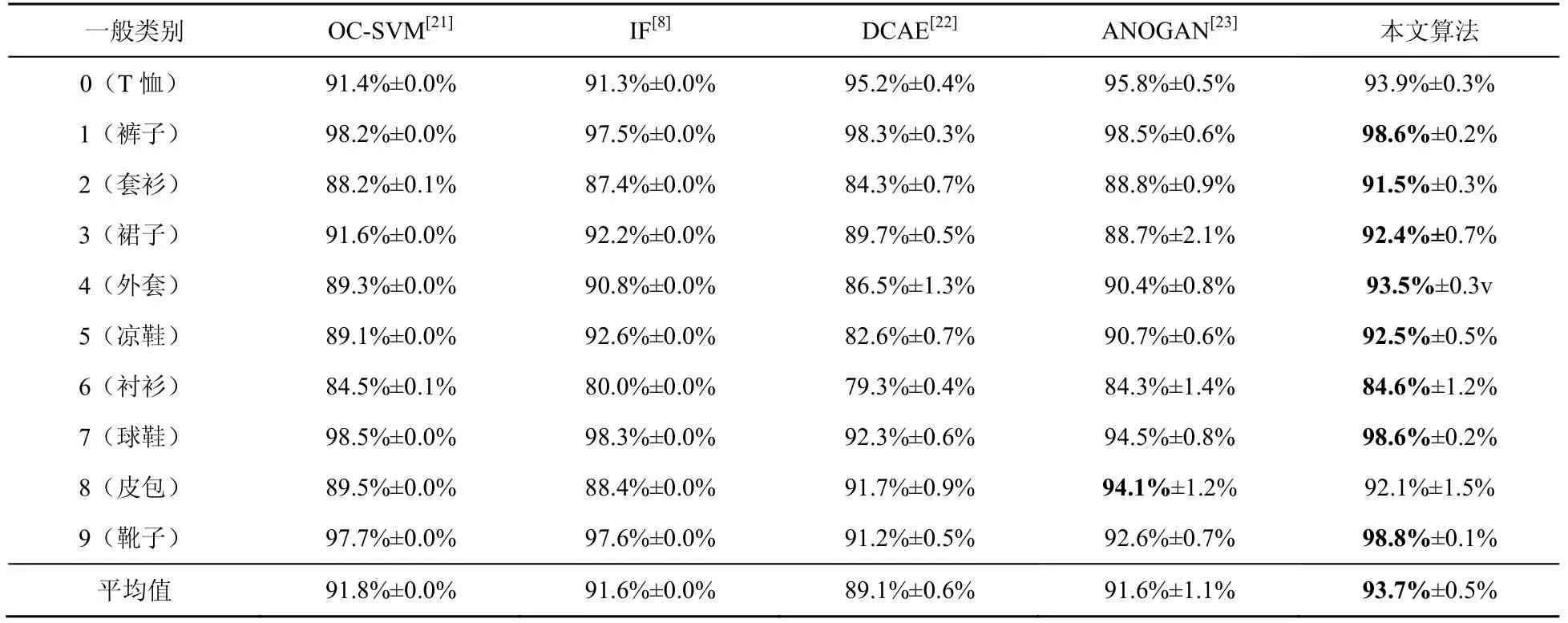
表3 Fashion-MNIST 数据集在各种异常检测方法下的实验结果对比

5 结束语

本文提出了一种基于混合高斯变分自编码网络的异常检测算法，采用混合高斯为先验构建变分自编码器提取数据特征，以自编码器构建深度支持向量网络压缩特征空间，寻找最小超球体分离正常数据与异常数据，并以此进行异常检测。实验结果表明，本文算法优于当前的一些异常检测方法，实现了较好的异常检测效果。然而，本文算法模型也有一定的不足，算法中高斯分量最佳混合系数的确定是根据混合系数与平均AUC值之间的曲线人为选择的，下一步的重点是建立优化模型来自适应地确定混合系数。