云制造任务分解模型

胡艳娟， 潘雪侨， 王占礼，张子玉， 许小侠， 李宗昊

(1.长春工业大学 机电工程学院， 吉林 长春 130012;2.长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

随着第三次工业革命的蓬勃发展以及互联网技术的广泛应用，传统制造行业面临被时代潮流淘汰的压力，不得不面临转型升级。为了快速响应客户的各种要求，缩短产品开发周期并降低研究成本，企业正转型升级为网络化制造及面向服务模式[1-2]。我国著名的大数据专家李伯虎[3]院士早在2010年就提出了云制造的理念，云制造作为一种新兴的有别于传统制造业的生产模式，展现了传统制造业与大数据互联网行业的紧密融合。云制造可以忽略企业的地域限制劣势，将各地的制造信息通过大数据的方式搜集于某一特定数据中心，为各地使用者提供信息服务，该服务远比过去传统的制造模式快速便捷。它糅合了过去网格化生产、应用服务商等各类生产方式，最后融合云计算的思想形成了当今的云制造概念。然而，制造资源的大量涌入以及制造资源的多样性，使得一个任务需要多方协助共同制造才能有效完成。所以，合理实现对制造任务的分解成为云制造平台的首要问题。

为了使云制造模式达到生产资源配备优化合理的目的，首先要对生产制造全过程进行合理分解。通过对该生产任务进行适当的任务分解，既能减小生产厂家的加工制造难度,增强生产制造加工效率，又能缩短生产厂商的资源配备时间。基于云制造模式下的生产制造问题，普遍较为复杂，而且层次分明，因此应该首先分析其制造任务中的内部联系。著名学者Dan B[4]通过运用公理化设计矩阵，将具体任务的内在联系矩阵化，清晰地表达出具体任务和其相应属性的联系。其他研究人员进一步对内部结构中的子任务间存在着相关关系进行研究，Gerasoulis A[5]在1993年为明确子任务和子任务间的划分，通过建立生产任务的相关性分析模型，利用聚类算法求出相应解，最后得出了粒度合适的子任务集合。以此项研究为基础，Chen S J等[6]在2003年表示可以通过处理子任务间的关联程度对子任务聚类评估，使繁多细小的子任务聚合成的任务更符合企业生产要求。另外，还有一些人通过生产制造任务的层次和关联程度来实现生产制造任务的分解。周珂等[7]在2009年提出将生产制造中的所有元素划分层次，从个体到整体，从零件到部件的层次分解办法，妥善解决了生产实际中任务分解不切实际导致资源配备散乱的问题。刘明周等[8]在2017年提出一种全新思路，通过一种新算法利用递归分解的方法对不同层次的任务分解。实际上，将复杂的任务分解为一组子任务，这样可以提高流程的可理解性并减少分析的难度。在这方面,Zhang Z等[9]提出了一种将繁琐的生产制造环节分解细化的方法。根据输入和输出关系构建基于GMPBN的两阶段分解算法,通过在子流程重建阶段评估分解算法，有效地找到最优解。

通过以上内容可以发现，近年来相关专家学者主要从生产任务的相关联系对制造活动进行分解。根据上述讨论结果，文中将对云制造环境下的任务分解开展进一步研究。

1 基于任务分层规划理论的模型建立

云制造平台任务分解是通过利用已有的生产要素，把需求者对该生产任务提出的要求作为原动力，进而把云端上的整体任务分化为几个符合实际生产的流程。因而，为了解决云平台的任务划分问题，一方面需要根据实际情况建立相应的数学模型；另一方面还需要基于该数学模型的特点选用更贴合的算法，通过算法计算出最优解,为云任务在平台资源池匹配更优质资源。任务分解过程就是化复杂为简单，通过将繁琐的生产制造流程按照现实情况分化为几个流程较为简单的阶段，这几个流程简单的阶段又可以将任务分成粒度适当的多种子任务，并构成不同的子任务集合。因而，子任务集合具有多样性的基本性质。所以，文中将任务按照产品的生产周期分成多个阶段，提出一种基于HTN分层任务规划的分解方法。

HTN规划是通过使用智能化规划求解方式，利用树状图的形式将一个复杂繁琐的总体任务逐步分解至可被直接执行的子任务的方法[10-11]。HTN规划的任务可以用三元组(S，T，D)表示。S是指任务的状态，表示任务是否分解完成;T=(T1,T2,…,Tn)是指需要进行规划的n个任务列表，表示任务规划的先后顺序;D是指论域，为操作和方法的集合，即与不同任务阶段相对应的分解方法。HTN规划的结果是一个可执行方案，即通过云平台的规划使复杂制造任务可以在生产周期中各个阶段得到最佳分解方案。各个阶段之间既存在关联,又可以独立执行，可以根据实际生产需求执行一个或多个阶段的任务分解。因此，如何将各个阶段合理分解成可执行的子任务成为文中研究重点。

1.1 建立设计任务的分解模型

通过云平台对产品进行设计，其本质是通过并行设计使得设计过程更符合实际情况。并行设计是指在一个新组建的设计项目组中，将不同学科、不同水平、不同专长的人集结起来，对该项目完成设计工作。该设计工作要从项目开展之前就考虑到所设计产品生命活动周期的全过程，通过多类型、多部门合作，对产品进行有机统一的设计，使得产品可以尽快投入生产。既节约了企业制造成本，又缩短了产品生产周期，提高了产品设计效率。

1.1.1 设计任务分解原则

设计任务包含众多相关子任务，这些子任务间相互存在着错综复杂的内在联系。对于设计任务来说，设计过程就是将所有子任务按照最佳匹配方式组合而成。子任务间都保持有一定的联系程度，这就使得设计工作人员要进行频繁沟通来保持各自的设计工作相互匹配。只有尽可能地使联系程度高的拆分到一起，降低不同子任务组间的联系，减少信息沟通量，才能保持子任务具有较高的独立性，所以引入任务关联耦合度的概念。在通过云平台进行设计任务分解时，子任务必须保证下列四个方面内容：

1)尽量使设计人员满意。分解后的子任务交给设计人员完成，应征求设计人员的意见，尽量使设计人员满意。通过设计系统的反馈来验证任务分解结果，实现对分解结果的修正，使设计任务更易完成。

2)遵循耦合值最小。在设计过程中通过任务耦合使联系紧密的子任务组合在一起，形成一个模块，让各模块具有相对独立性，减少模块之间的信息交互，以便减少开发时间、提高产品质量。

3)保留特殊设计需求。针对某些设计任务时，应考虑到用户需求对设计的影响。保留用户对产品设计时的特殊要求，在产品设计过程中保证特殊结构或加工方式的完整性，防止对其拆分。

4)保持适度的粒度。粒度是子任务数量与层级划分的总体概括，当粒度太小时，子任务数量偏高，工作较为零散，不便于对子任务进行管理控制；当粒度太大时，子任务数量偏少，工作压力较大，相互联系较广，不便于对子任务求解。所以需要通过任务分解机制不断优化分解粒度，最终找到适中的子任务粒度。

1.1.2 设计任务数学模型

可以定义Sij为满意度，j为设计组，Ti为任务。此时Sij代表设计组对任务的满意程度。满意度Sij可以设置成一个模糊的变量集合，子集为很不满意、不满意、一般、满意、很满意5种，同时将这5种情况用数据直观量化：0，0.25，0.50，0.75，1。

此时可知，平均满意度公式为

(1)

式中：m----设计组的个数。

先把产品的设计任务看作一个总体任务，按照功能类别分类，将其分解为几个子任务，当子任务无法继续分解时，称之为最小子任务。若是还可以继续分解，就可以通过式(1)对该子任务进行一个满意度检测。此时，要引入一个阈值λ，λ取值为0～1，该数值视情况而定。具体分解步骤如下：

1)先把产品的设计任务看做一个总体任务，按照功能类别分别将其分解为几个子任务Ti(i=1，2，…,n)。

2)当子任务无法继续分解下去时，则分解到此为止；若是还可以继续分解，就通过式(1)对该子任务进行一个满意度检测。

3)经过检测得出的满意度低于阈值λ，则该子任务继续进行分解，直到分解出的子任务满意度高于设定阈值λ。

4)对整体合理性进行判断，完成设计任务树状结构分解。

对于满意度S的具体定义，可以从平台、服务、客户三个方面考虑。平台方面包括对结构满意度、材料满意度和可行性满意度；服务方面包括人员素质、服务价格、设计理念；客户方面包括性能需求、信誉度。通过式(1)算出其平均满意度，将其与阈值λ进行比较，需达到各子任务的规定标准，同时满足产品整体的属性需求。

根据任务节点数据以任务间的相互联系建立设计结构矩阵。设计结构矩阵的维数代表设计任务的数量，该矩阵的每一行都代表完成本项任务所需其他任务的输出支持。每一列代表完成本项任务所需其他任务的输入支持。

设计结构矩阵为

(2)

在式(2)矩阵中，A表示矩阵本身，由n个任务构成，任务可以用Ti(i=1，2，…，n)表示，对角线元素代表该项设计任务。各项设计任务之间的信息流通用aij表示，当任务Ti对任务Tj有信息流通时，aij=1；当任务Ti没有对任务Tj有信息流通时，aij=0。

在现实情况中，各种子任务间联系程度有强有弱。因此在设计结构矩阵中，需要明确不同子任务之间的联系关系，所以文中采用模糊集理论的方法解决问题。该理论的提出也正是由于很多情况无法单一表示出来，需通过将不同信息量化为可被处理的具体数据，以此提高对描述不同任务之间关联的准确性。在云制造的设计任务分解中，根据不同设计子任务间相互作用关系的大小，设置了一个模糊变量集合，通过弱、较弱、中、较强、强5种程度表示[12]，同时将其分别用数据0、0.25、0.50、0.75、1来直观量化。用该数值代表矩阵中的各类元素，A矩阵也转变为数值矩阵P,

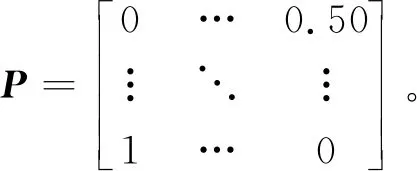
(3)

经过这一转变，该矩阵一方面可以清晰地看出各项设计任务有无信息流通，另一方面还可以表示任务间联系程度的强弱。至此，完成对设计任务矩阵化建模。

1.2 建立制造任务的分解模型

由于产品结构越来越复杂，一个部件就可能由成千上万的零件构成，这些零件之间或多或少存在一些联系，因此需要把不同的资源协同后再进行加工。所以有效地制造任务分解方法是解决问题的关键，通过合适的制造任务分解方法，使产品的生产效率提高。

1.2.1 制造任务分解原则

制造任务可以按照一定的分解方式划分成不同的子任务，而这些子任务之间存在着相互依赖的关系。但由于是通过设计任务而来，使得制造任务之间不需要相交互的信息,只需要根据设计任务属性不同，分解成不同的制造子任务进行制造加工。所以，云平台的制造任务在分解时，子任务要保证下列原则：

1)可匹配。分解后的子任务交给车间加工，子任务是否有可以加工的资源，即需满足在资源池中可找到能匹配的资源。

2)相对独立。在对设计产品加工过程中应满足生产要求，能进行一次加工完成的工序尽量集中到一起。防止之后运输过程中对加工产品造成非必要损伤，导致成本和废品率上升。

3)便于管理。当任务分解后，各子任务的生产加工要由车间来实现，并通过云平台对其进行管理控制。

4)内聚性最大。由于分解后的子任务存在多种聚合可能，需要选取最优的组合方案。在保证分解方案可行性的条件下，引入子任务间聚合系数，选取组间内聚值总和最大的组合方案。

5)特殊加工。对于加工的特殊工件，如需要不间隔连续工序加工或完成工序后要立即进行特殊处理等，则需要按照要求保证加工过程的完整性，不得进行拆分。

1.2.2 制造任务分解数学模型

在制造任务中，一般工序步骤极其分明，都是由工序到零件、从零件到部件、从部件到产品逐级完成，层次划分清晰，联系也较为紧密。常见的工业产品一般都是在上一代旧产品的基础上进行改造升级，其内部结构一般来说不会有结构性改变，很少有完全原创的产品出现。工作分解结构(WBS)是一种将项目依据内部关系分解为层次结构的任务分解方式，参考云平台产品库中同类产品结构，依靠WBS使得制造任务更容易分解。由于将制造任务分化至工序级会导致产生极大的输送费用，因此在生产实际中，一般把最小生产制造任务单元定在零件级。

云制造的最小任务即元任务间具有很强的相互约束联系作用，而这些任务的先后顺序相对固定。一般来说，任务的约束结构有串行、并行、循环、选择约束四类。串行约束结构是指该项生产任务的几项元任务有明确的先后顺序，不得违背顺序进行生产加工；并行约束是指该生产任务的几项元任务没有明确先后顺序，可以同时生产加工；循环约束是指这些元任务可以多次循环完成，顺序也很固定；选择约束是指生产过程中可根据生产情况决定加工方式，对下一个任务没有影响。可依据任务约束的结构，对任务间的相互关系进行计算，获得制造任务间的内聚系数。

1.2.2.1 任务关联系数

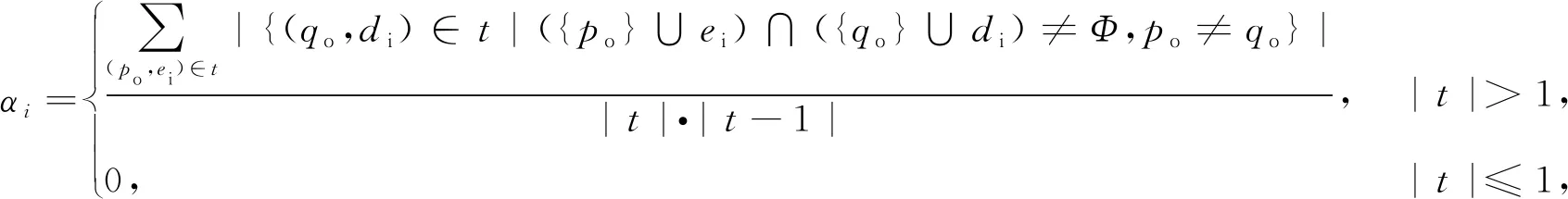
(4)

式中：|t|----元任务的数量;

po、qo----输出元任务；

ei、di----输入元任务；

∑----当qo≠po时，每个子任务和其他子任务相互联系的次数总和。

1.2.2.2 任务重用系数

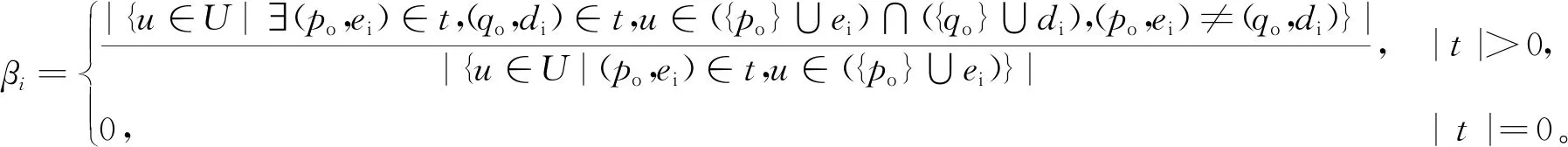
(5)

1.2.2.3 任务内聚系数

任务内聚系数Ci是对任务内聚性的综合度量，是任务关联系数αi与任务重用系数βi的乘积，可以利用下式计算求得，

Ci=αi×βi。

(6)

任务内聚系数反映了生产任务中各子任务的关联水平，通过其关联水平也可以看出子任务的工作量大小，即粒度大小。生产制造的子任务粒度可以通过任务粒度系数和任务数量两项指标说明。任务粒度系数越大，说明子任务数越少，任务分解不到位，生产制造工作较为复杂；任务粒度系数越小，说明任务数量越多，生产中考虑的任务总量越多。为避免生产过程中追求高度聚合状态，使得子任务分解至元任务层，可以通过任务粒度相互比较来修正。Ai是指任务耦合系数，Ci是指内聚系数，那么粒度的表示就可用耦合系数除以内聚系数进行衡量，公式如下

(7)

则云制造任务整体的任务粒度度量可用各个子任务的粒度度量均值表示，即

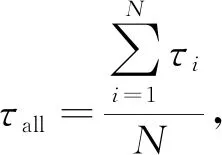
(8)

当τall越大的时候，任务粒度的配置就越不合理，云任务分解出的各类生产加工子任务内聚程度越低。根据上述计算结果建立矩阵，完成制造任务分解模型。

1.3 建立运输任务的分解模型

生产制造过程中的运输任务是由于分解为网格状的制造子任务之间产生的资源输送需求。当面对复杂的制造子任务时，由于运输服务受区域性和运输量的限制，所以整体的运输任务也需要依据制造任务的属性将其分解成若干子任务[13]。此时可以分别匹配相应合适的输送资源，从而达到最优的运输效果。

通过逐一寻找符合要求的运输资源，以达到运输效率的最大化。依据上述描述建立相对应的数学模型：

1)运输时间目标函数T。根据运输任务要求对候选资源集合中运输资源进行搜索匹配，因此运输资源优化时间函数

T=T1+T2+…+Tn，

(9)

运输时间T的约束为

T≤Tmax,

(10)

式中：Tmax----最晚交货期限。

2)运输成本目标函数C。根据运输任务要求对候选资源集合中运输资源进行搜索匹配，因此运输资源优化匹配的运输成本函数

C=C1+C2+…+Cn，

(11)

运输成本C的约束为

C≤Cmax,

(12)

式中：Cmax----客户所规定的最高成本。

3)运输质量目标函数Q。根据运输任务要求对候选资源集合中运输资源进行搜索匹配，因此运输资源优化匹配的加工质量函数

Q=Q1+Q2+…+Qn,

(13)

运输质量Q的约束为

Q≥Qmin,

(14)

式中：Qmin----客户规定最低服务质量。

4)运输能力目标函数Tr。根据运输任务要求对候选资源集合中运输资源进行搜索匹配，Tri表示运输服务各阶段所能承受的最大运载量，因此运输资源能力Tr的约束为

Tr≤min{Tr1,Tr2,Tr3,…,Trn}。

(15)

根据上述约束可建立适应度函数

(16)

1.4 建立维护任务的分解模型

维护任务贯穿整个产品工作周期，但根据维护类型的不同、维护技术的高低、维护工作量的大小，可以把维护任务按照不同类型、不同工作量的方式分解任务，类型包括提前预防、紧急维护、针对维护三类，工作量分为大中小三类。同时借鉴模糊集合的思想，对其进行模糊分类，在分别满足技术要求和工作量的条件下，完成相应维修资源选择。

由于日常维护任务的可选服务种类繁多、服务能力不同，所以云平台需要把所有可提供服务的资源整合到一起，形成一个统一的整体，便于后期维护任务分解后的服务选择。在整合资源时，平台要综合考虑服务是否能够完成所需维护任务以及完成维护任务效率的高低，考虑的因素包括几个衡量指标：

1)工作时间(T)。指需维护的资源所运行的工作时间。

2)损耗程度(W)。指需维护的资源在不同工作条件下设备损耗的程度。

3)服务区域(D)。指维护任务发布方对服务资源要求的服务区域。

4)服务能力(B)。指维护服务的执行效率及服务质量。

5)服务信誉(C)。指维护任务发布方对服务资源守信程度的认可情况，该指标可直接采用所有历史信誉评价的平均值计算得出。

综合以上指标可构建出运输任务的形式化描述模型

ST(i)={ID(i);Name(i);Type(i);

T(i);W(i);D(i);B(i);C(i)}。

2 分解过程的实现

文中采用设计、制造、运输、维护四个阶段，按照HTN分层规划理论模型的步骤分别对各阶段模型进行求解，最终实现在云制造环境下任务的全生命周期分解。

首先，设计阶段采用应用图论的知识来解决。设有向图H=[V,E]，V代表有限的顶点集合，E代表有限边的集合，此时边与点相对应的假定顶点表现出从v1到vn的次序，则n阶方阵

(17)

为H的邻接矩阵(i，j= 1，2，…,n)，其中，

(18)

此时可以将设计任务当做一个节点，而任务之间的相互联系被看作有向边，那么设计结构矩阵本质上就是有向图的邻接矩阵。

对此结构矩阵可以取其一部分，形成简单的布尔矩阵，进行运算求解。该任务集合的每个子集都代表一个任务，且都不会出现没有元素的情况，当其只有一个元素时，说明该任务只有一个子任务，当其包含多个元素时，说明它有多个子任务。通过这样的方式，可以把子任务通过不同的排列组合方式形成最佳任务组合，为之后的资源配置提供了理论基础。具体思路如下：

1)将每个子任务当作顶点，即矩阵行或列全部子任务。设定矩阵中随机顶点为v0初始点，从此点出发，访问其余各点。

2)找出v0的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。

3)返回前一个访问过的仍有未被访问邻接点的顶点，继续访问该顶点的下一个未被访问的邻接点。

4)重复2)、3)步骤，直至所有顶点均被访问，搜索结束。每次访问的组合即为最优组合，因此设计任务分解完成。

制造阶段可以通过BGLL算法来解决任务分解问题[14]。由于一些复杂的制造任务有上百个元任务，此时可以把这些任务看作是一个新有向图N=[V，E]。

在该繁琐网络中，节点与节点中间的边的数量被称为度，它表示节点的连接密度。则该任务节点vi∈V的度就是指相连几个边的权重和，即

(19)

则网络的总权重Lw，即加权任务网络所有边的权重和可以利用下式计算，

(20)

优秀的网格划分应该增加图团体内部边，减少外部边。为了衡量该网格划分的质量，文中用模块度来衡量其划分质量，模块度是指图团体内部边的数量减去预期边的数量，该数量值越大,说明该网格划分质量越高。内部的关联越是密切，那么边的比重越大，所以模块度的定义公式为

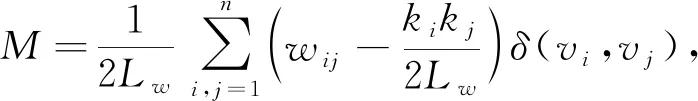
(21)

式中：wij----矩阵W中第i行，第j列的数值，该数值可以体现出两个节点任务的联系程度；

n----元任务节点的数量；

ki----节点i所有相接边的权值和；

δ(vi,vj)----两个节点的归属情况，都属于同一个团体时为1，不属于同一团体时为0。

由于规定模块度上限为1,下限为0，因而越靠近1,就说明划分情况越理想，但在实际生产过程中基本不可能达到这个数值，一般定义0.4～0.7的模块度最为理想。所以,通过上述方法得出模块度最高的结构就可得出最好的聚类结果，步骤如下：

1)将每一个任务节点都当作一个团体，根据相应算法得出模块度。

2)随机聚合两项团体，并将该团体视为单独节点，计算其模块度的大小幅度差距，该差距计算公式为

(22)

3)将2)计算出的数值列出，取其中最大的两项继续进行聚合，计算其关联度和模块度。

4)循环2)和3)，直到整个网格都被聚合为一个团体。

5)通过比较所有数据，模块度最高的结构就是最优聚类结果。

6)通过计算中间过程各个团体的粒度的平均值，作为该任务节点的整体粒度度量，如果低于预定阈值，那么重新划分网络结构并重新计算，直到平均值超过预定阈值。

通过上述6步，云制造的各阶段分解任务结束，最终得出的结果就是符合要求的子任务。

运输阶段通过蜂群算法[15]模拟蜂群可以很好地演化搜索过程，对适应度函数进行求解，其具体流程如图1所示。

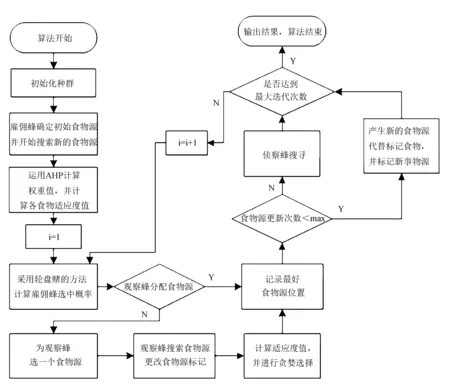
图1 算法流程

维护阶段采用集合的形式对信息进行描述，通过引入资源维护数据库对资源的工作状况进行评估。由于不同产品工作时间和工作损耗存在区别，应从数据库中选取相应符合实际工作情况的数据，通过语义判断的方式选择合适的维护类型，最终筛选出维护方案,并将维护子任务分配给相应企业。至此，完成从设计阶段到维护阶段全生命周期的任务分解模型，实现了在云制造环境下对任务的分解。

3 结 语

云制造资源的复杂和庞大使得云制造任务在各资源间协同工作的选择更加多样化。为了节约生产成本，合理利用闲置资源，提高生产效率，不得不寻找更加适合的任务分解方法。文中通过研究云平台复杂任务的特征属性，建立了云环境下复杂制造任务数学模型，主要包括设计、制造、运输和维护四个阶段。然后根据客户对不同任务分解要求的不同，选择执行一个阶段或多个阶段。采用层次分析法建立系统框架，利用深度优化算法、快速模块化优化算法和人工蜂群算法构建了一套任务分解方法，最终得到适合云平台的任务分解方案。文中所提出的任务分解方法可为云制造平台进一步研究提供理论与方法支持。