基于车辆-轨道耦合动力仿真的轨道连续多波高低不平顺控制标准建议

李国龙,杨 飞,李建辉,张 煜,严乃杰

(1.中国铁道科学研究院集团有限公司基础设施检测研究所,北京 100081； 2.中国铁路南宁局集团有限公司,南宁 530029； 3.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081)

中国高速铁路最高运营速度已达350 km/h，对车辆运行的安全性和平稳性提出了更高的要求[1]，轨道几何不平顺作为轮轨激励是引起车辆振动的主要原因[2-5]，而连续多波不平顺更易引起车辆激振，对行车安全性和乘坐舒适性更为不利[6]。当轨道不平顺在某一频率重复时，会引起车辆悬架的谐波响应，能量不断积累，大大增加了列车的脱轨风险，英国在其标准中给出了明确规定[7]。美国针对高低和轨向的单波和多波不平顺分别制定了养护维修标准，高低单波为13 mm，连续多波为10 mm[8]。

我国的普速、高速铁路维修规则，如《普速铁路线路维修规则》、《高速铁路有砟轨道线路维修规则》、《高速铁路无砟轨道线路维修规则》等都非常重视轨道的连续多波不平顺，均对其做了相应说明，但由于缺乏研究，管理值不明确，对现场指导性不强。如《普速铁路线路维修规则》中明确应重视周期性连续三波及多波轨道不平顺的判别，对于幅值达到14 mm的连续多波高低不平顺，需要及时处理，但并未指明相应速度等级；高速铁路维修规则中只说明要避免出现连续三波及多波轨道不平顺。

目前已运营高速铁路线路中已经出现三波甚至多波不平顺现象，比如，连续轨道板上拱[9]，路基冻胀、桥梁徐变[10-11]等，均会产生轨道连续多波高低不平顺。由于高速铁路线路的横向稳定性较好，所以对线路不平顺影响主要体现在高低变化上，因此，高低连续多波不平顺管理标准的制定就显得尤为重要。重点分析连续多波高低不平顺波长和幅值对车辆动力学性能的影响规律，将轨道高低不平顺简化为不同波长、不同幅值的连续正弦波形式，基于车辆-轨道耦合动力学模型进行仿真分析。根据轮重减载率和车体垂向振动加速度确定敏感性波长[12]，基于敏感波长，调整不平顺幅值，确定适用于不同速度等级的高低连续多波不平顺容许偏差管理值。

1 模型建立及验证

1.1 车辆模型

列车模型中可以含有多节车辆，每节车辆包含1个车体、2个转向架和4个轮对，针对二系悬挂客车进行分析，分别考虑其横移、沉浮、侧滚、点头(旋转)、摇头共计35个独立自由度，具体见表1。车辆动力分析模型如图1所示，图中各变量对应的意义具体参见文献[13-14]。

表1 车辆模型自由度

图1 车辆动力分析模型

1.2 轨道结构动力分析模型

轨道结构的弹性变形作用既可以起到过渡轮轨高频振动的目的，还对轮轨力有显著影响[15]。为了更真实地表现出钢轨的局部振动特性，采用有限元法分别建立钢轨系统和轨道板CRTSⅠ空间模型[3，16]，如图2、图3所示，用弹簧-阻尼单元模拟扣件对钢轨的约束，采用强迫振动理论[3]处理钢轨系统和轨道板之间的相互作用。

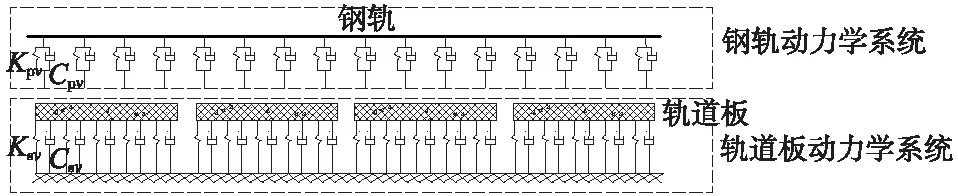
图2 轨道结构动力学模型

钢轨系统和轨道板的阻尼矩阵首先采用Rayleigh阻尼的形式，同时根据“对号入座”考虑扣件对钢轨系统刚度矩阵和阻尼矩阵的影响，Rayleigh阻尼计算如下

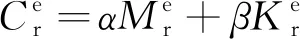
(1)

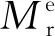
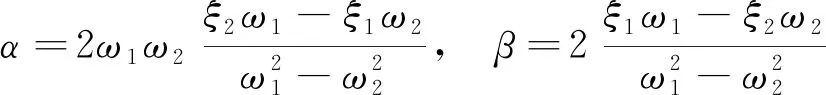
(2)

式中，ω1、ω2、ξ1、ξ2分别为结构的一阶、二阶自振频率与相应的阻尼系数。对钢轨，ξ1、ξ2取1%[17-19]，对轨道板、桥梁等混凝土结构，ξ1、ξ2取为2%[16]。

轨下胶垫垂向静刚度取25 MN/m，阻尼取75 kN·s/m；横向静刚度取20 MN/m，阻尼取60 kN·s/m[14-16]。

1.3 轮轨动态相互作用原理

轮轨法向采用Hertz非线性弹性接触理论，轮轨之间的垂向力可表示为

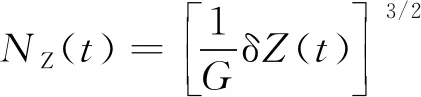
(3)

式中，G为轮轨接触常数，m/N2/3；δZ(t)为轮轨间的弹性压缩量，m。

轮轨蠕滑力首先采用Kalker线性蠕滑理论求解轮轨间的纵向、横向和自旋蠕滑力，公式如下

(4)

然后利用Shen-Hedrick-Elkins理论对轮轨间纵向和横向蠕滑力进行非线性修正，具体计算方法及式中参数说明详见文献[14]。

1.4 车辆-轨道耦合方程的建立及数值求解方法

车辆、轨道组成动力仿真分析系统，通过轮轨力进行耦合。系统振动在任意时刻应满足力的平衡条件和变形协调条件。大系统运动方程可用式(5)表示

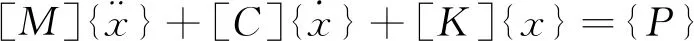
(5)

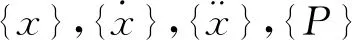
(6)

(7)

[M]、[C]、[K]分别表示整个系统的质量矩阵、阻尼矩阵、刚度矩阵，其公式为

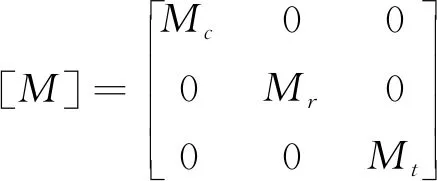
(8)

(9)

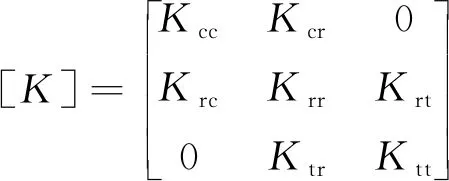
(10)

Newmark-β方法[20]是一种无条件稳定的隐式积分格式，属于自起步方法，对时间步长Δt的取值不影响解的稳定性，取5×10-5s。

1.5 模型验证

采用文献[21]中四方车辆厂准高速列车，以120 km/h的速度通过，波长为20 m，幅值为10 mm的高低连续谐波不平顺，如图4所示。计算结果与文献[22]进行对比，车体垂向振动加速度在±0.529 m/s2之间，如图5所示，时程曲线的变化形式和计算结果与文献结果基本相同，轮轨垂向力范围为45.384～55.092 kN，如图6所示，与文献结果稍有差异，是由于模型采用了不同的轨道结构形式。

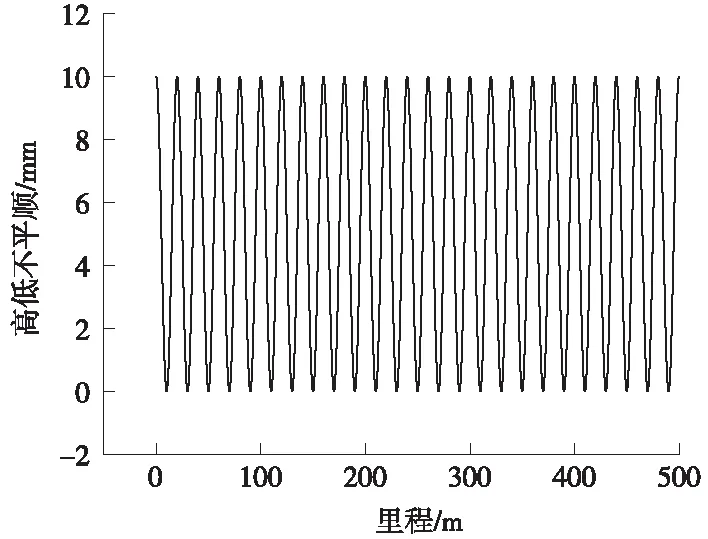
图4 单侧轨道高低不平顺

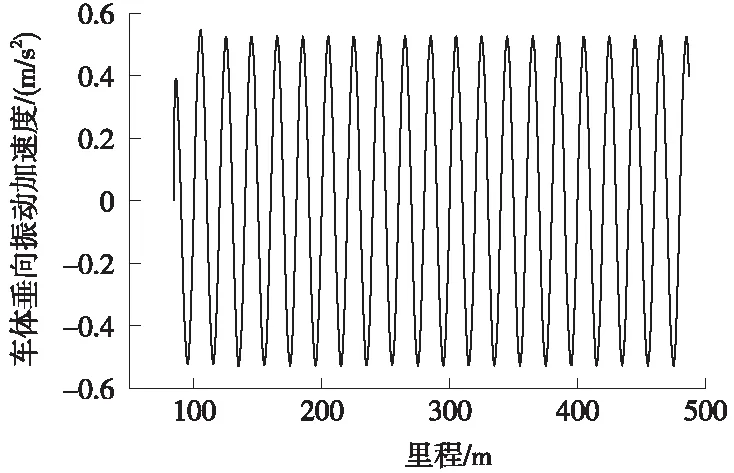
图5 车体垂向振动加速度

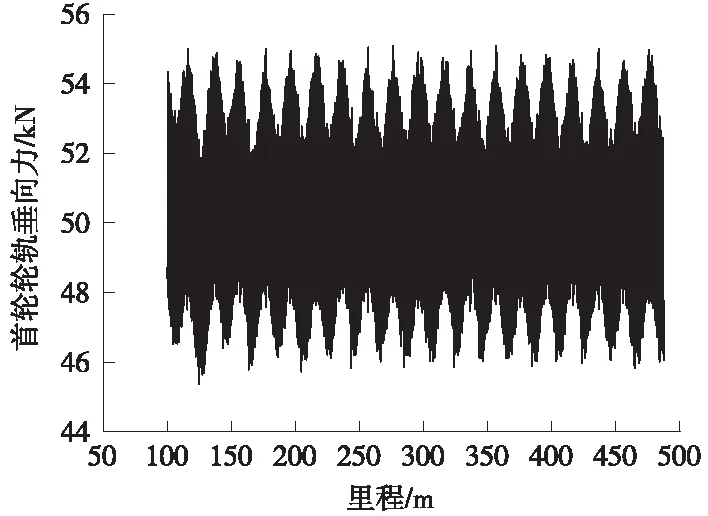
图6 轮轨垂向力

根据中国铁道科学研究院2013年在厦深高铁进行的三波高低不平顺预设实测试验，设置连续3个波长为10 m，幅值为+4 mm的余弦波模拟高低几何不平顺，采用高速综合检测列车2010参数，运行速度为240 km/h，进行车辆-轨道耦合动力仿真分析，轮重减载率计算值为0.433，实测结果根据上下行分别为0.47和0.43，综上所述，模型准确可靠。

2 敏感波长确定

2.1 连续多波高低不平顺

实际线路中，随机不平顺可以被简化成各种谐波形式，在静态弦测法中，也是假设轨道不平顺为多种谐波，同时在高速铁路轨道不平顺的预设试验中，也经常通过人为设置单个或者多个谐波不平顺，根据列车经过时的动力响应从而获取不平顺的管理限值。由于实测轨道几何不平顺随机性较强，为了更好地表现高低不平顺对行车的影响，轨道线路管理多采用半峰管理值，基于此选取正弦波形式的轨道高低不平顺，具体如下

Z=Asin(2πx/λ)

(11)

其中，A为不平顺半峰值；x为轨道纵向距离；λ为轨道不平顺波长。

2.2 仿真计算与分析

为确定高速列车对轨道连续多波不平顺的敏感波长，给定不平顺半峰值A=4 mm，设置波长λ分别为2、4、6、8、10、12、14、16、18、20、25、30 m共12种波长成分，线路总长500 m，采用CRH380A型列车，列车分别以80、120、160、200、250、300、350 km/h的速度通过，根据车体垂向振动加速度和轮重减载率分析不同波长成分对列车响应的影响规律，由于谐波形式的轨道几何不平顺引起的车体垂向振动加速度频率相对单一，且不考虑轨向不平顺，因此不考察Sperling指标和脱轨系数的影响。

根据计算结果，当不平顺波长为2 m和4 m时，车速分别达到160 km/h和300 km/h时轮重减载率超过《高速动车组整车试验规范》中规定限值，但由于轨道线路中小于4 m的连续多波不平顺多数为钢轨弯曲不平顺，幅值很小，因此其不作为控制指标[23]；轨道不平顺波长为6 m和8 m时，车体垂向振动加速度分别在200 km/h和250 km/h存在明显共振的现象；当轨道不平顺的波长为10 m和12 m时，相对于其他波长的轨道几何不平顺引起的车体垂向加速度和轮重减载率明显增大，当速度为350 km/h时，车体垂向振动加速度已经达到《高速铁路有砟轨道线路维修规则》和《高速铁路无砟轨道线路维修规则》中关于车体垂向振动加速度的Ⅲ级2.0 m/s2的临时补修的管理标准，计算结果见图7～图10。

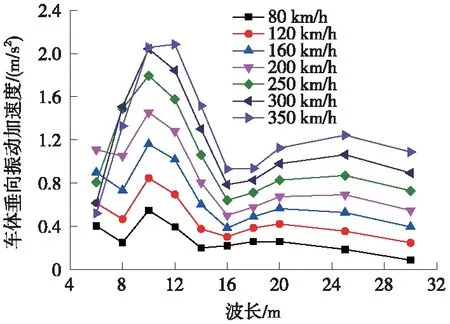
图7 不同速度条件下车体垂向振动加速度趋势

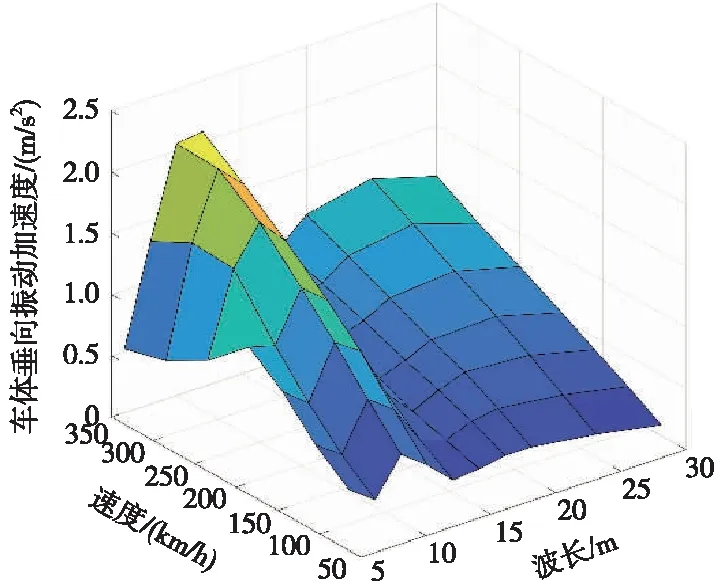
图8 车体垂向振动加速度随波长和速度的变化趋势

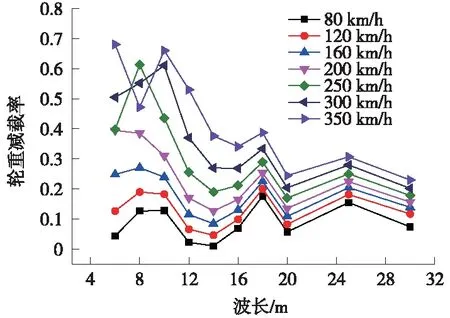
图9 不同速度条件下轮重减载率变化趋势

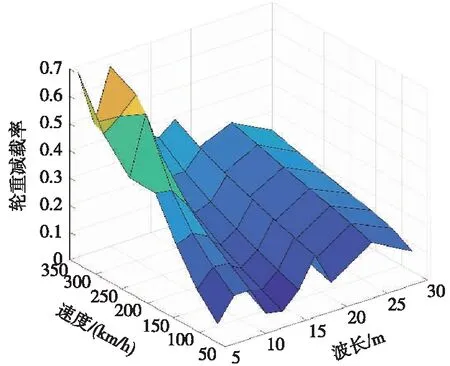
图10 轮重减载率随波长和速度的变化趋势

3 管理幅值确定

为更好地研究连续多波高低不平顺对行车的影响，确定控制管理标准，根据上一节中可知轨道几何不平顺波长10 m和12 m是列车的敏感波长，所以针对10 m和12 m波长，调整幅值分别为2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、18、20、21 mm(不平顺波长为12 m时，幅值只计算到了16 mm)，进行车辆-轨道耦合动力仿真计算，获取车体的动力响应和轮重减载率，计算结果见图11～图14。由计算结果可知，高低不平顺10 m波长相对于12 m对行车安全更加不利，因此以波长为10 m时的计算结果作为参考，给出控制标准建议值；当列车速度一定时，车体垂向振动加速度和轮重减载率随不平顺幅值增加呈现近似线性增长趋势；当不平顺幅值一定时，速度越高，轮重减载率增长越快，而车体垂向振动加速度随着速度的提高基本呈现线性增长。

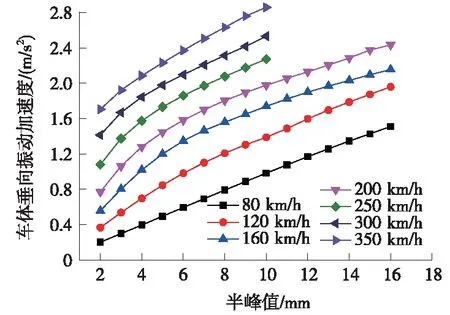
图12 波长为12 m时车体垂向振动加速度

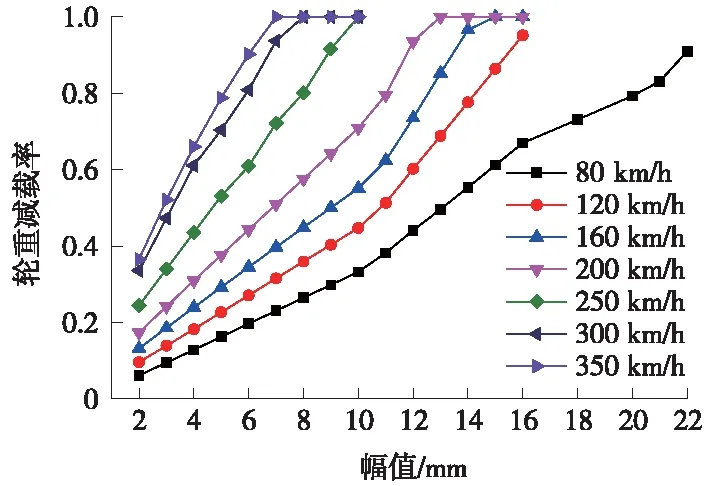
图13 轨道高低不平顺波长为10 m条件下轮重减载率

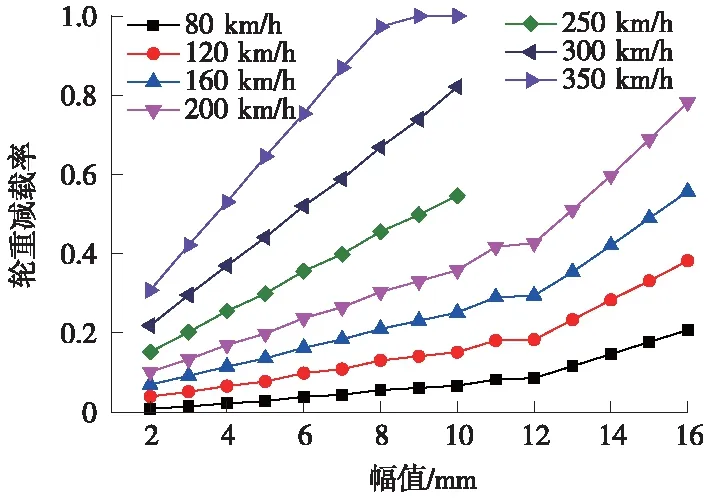
图14 轨道高低不平顺波长为12 m条件下轮重减载率

根据铁运[2012]83号《高速铁路无砟轨道线路维修规则》规定，车体垂向振动加速度到Ⅲ级临时补修管理标准为2.0 m/s2，Ⅳ级临时限速标准为2.5 m/s2，《高速动车组整车试验规范》中车辆动力学指标管理值中关于动态轮重减载率标准要求为0.8，我国在南津浦线脱轨试验中规定为0.8，以及郑武线240 km/h高速试验中，动态轮重减载率限值为0.9，依然可以保证行车安全[18]。由此对连续多波高低不平顺控制标准提出如下建议：速度在80 km/h(包含)以下的控制标准取20 mm(半峰值)，80(不含)～120 km/h速度等级下取14 mm(半峰值)，120(不含)～160 km/h速度等级下取12 mm(半峰值)，160(不含)～200 km/h速度等级下取11 mm(半峰值)，200(不含)～250 km/h速度等级下取8 mm(半峰值)，250(不含)～350 km/h速度等级下取5 mm(半峰值)，超过控制值后需要及时处理。

4 结论

通过建立车辆-轨道空间耦合动力分析模型，不仅可以较好地反映轨道不平顺对行车的影响，还可以更好地反映钢轨自身的振动特性。采用连续正弦波形式模拟轨道中连续多波高低不平顺，符合我国轨道线路管理的要求，主要结论如下。

(1)通过计算得知，10 m和12 m波长的连续多波高低不平顺对行车安全性和乘坐舒适性影响较大，尤其是当波长为10 m时，对轮重减载率影响更加明显，威胁行车安全，因此在轨道养护维修过程中要关注10 m波长下的连续多波高低不平顺的情况。

(2)当连续多波不平顺的波长和速度一定时，车体垂向振动加速度和轮重减载率随幅值呈线性增长趋势；当波长和幅值一定时，随着速度的提高，车体垂向振动加速度基本呈现线性增长，轮重减载率对速度不小于250 km/h时更加敏感，速度越大，轮重减载率增长越快。

(3)根据仿真计算结果，提出了不同速度等级下连续多波高低不平顺容许偏差管理建议值，速度在80 km/h(包含)以下取20 mm(半峰值)，80(不含)～120 km/h速度等级取14 mm(半峰值)，120(不含)～160 km/h速度等级取12 mm(半峰值)，160(不含)～200 km/h速度等级取11 mm(半峰值)，200(不含)～250 km/h速度等级取8 mm(半峰值)，250(不含)～350 km/h速度等级取5 mm(半峰值)，超过控制值后需要及时处理。