一类具有信号回路的趋化性模型解的存在性

（西华师范大学数学与信息学院，四川 南充 637002）

本文主要对以下具有信号回路的趋化模型进行研究，

该模型是文献[1]中提出的趋化模型的简化，其中，Ω ⊂R2是一个具有光滑边界的有界区域，表示关于边界∂ Ω的外法向量ν的导数，未知函数u(x,t)、v(x,t)、w(x,t)和z(x,t)分别表示巨噬细胞密度、乳腺癌细胞密度、CSF-1 的浓度和EGF 的浓度，参数 χ1、χ2和 χ3分别表示巨噬细胞、乳腺癌细胞和乳腺癌细胞系中CSF-1/CSF -1R 自分泌信号回路的趋化系数，参数s1、s2分别表示乳腺癌细胞分泌CSF-1 和巨噬细胞分泌EGF 的速率，参数r1、r2分别表示CSF 和EGF 的均匀降解速率。假设参数s1、s2、r1、r2都是正常数，初始值u0、v0、w0和z0都是非负函数。

该模型描述了乳腺癌细胞和巨噬细胞在短期化学信号回路中的趋化性行为。巨噬细胞分泌EGF，一方面有自身的自由扩散；另一方面会朝向由乳腺癌细胞所分泌的CSF-1 的浓度梯度方向做趋化性运动。乳腺癌细胞通过操纵固定的巨噬细胞信号来迁移，乳腺癌细胞分泌CSF-1，一方面可与巨噬细胞上的CSF-1 受体结合激活巨噬细胞向CSF-1 梯度趋化并分泌EGF；另一方面EGF 可以与乳腺癌细胞上的受体结合，这样就激活了循环链，激活的乳腺癌细胞通过分泌更多的CSF-1 并向EGF 梯度方向做趋化运动[2 − 4]，这一过程导致了短距离趋化信号回路。

目前对于模型（1）相关模型的研究已经取得了很大的进展，比如，Tao 等[5]研究了模型（1）当τ=0，χ3=0时解的全局存在性，并得到了当两种物质的总质量都很小时模型解的全局有界性与爆破现象。Li 等[6]进一步讨论了τ=1,χ3=0时解的全局存在性，同样得到了相应的模型在初始细胞质量都很小时解的全局有界性和爆破现象。Lin 等[7]对具有信号回路的情况进行研究并证明了当τ=0时模型（1）解的全局存在性和爆破现象。然而当τ=1时模型（1）解的性质目前尚未看到研究结果，为此在本文中主要讨论τ =1,χ3＞0时，在二维有界域中模型（1）解的全局存在性和有界性。

1 预备知识和主要结果

我们首先叙述模型（1）当τ=1时解的局部存在性，局部存在性的证明方法与文献[8]中方法类似，所以本文省略了证明过程。

引理1（解的局部存在性）设χi∈R(i=1,2,3)，则对于任意的非负初始值存在Tmax∈(0,∞)使得问题（1）存在一个非负经典解（Tmax表示最大存在的时间）。且当Tmax<∞，有

下面关于解的L1估计，将会在我们的证明过程中频繁使用。

引理2设都是非负的，且对于任意的x∈Ω及t＞0，都有u(x,t)和v(x,t)是正的。其中(u,v,w,z)是模型（1）的经典解，则对于所有的t∈(0,Tmax)，有

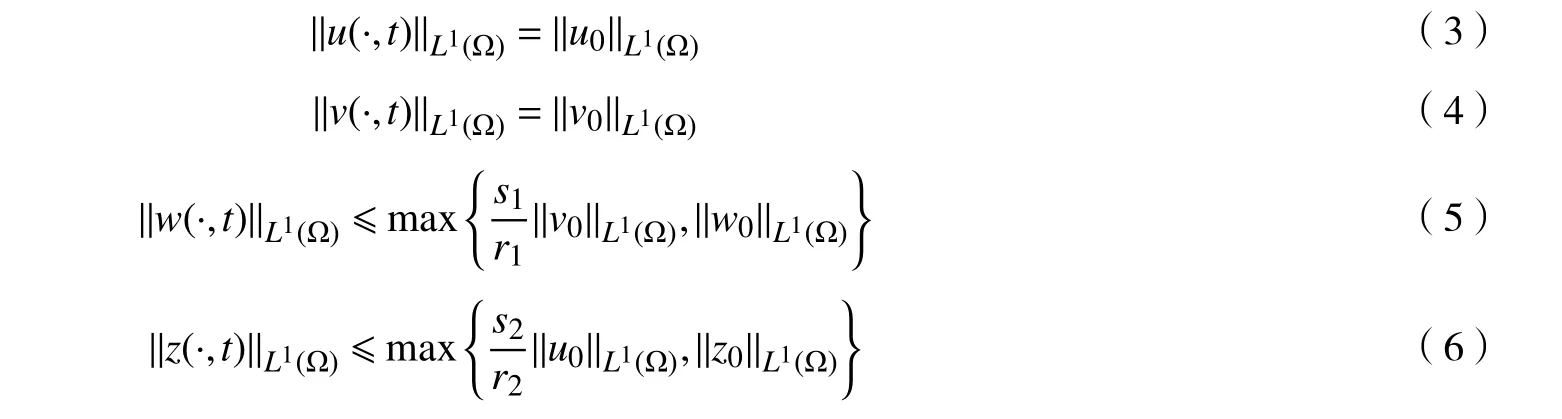
证：对式(1)中的第1 个和第2 个方程在 Ω上进行积分，有

因此推出了式(3)和式(4)。同样对式(1)中的第3 个和第4 个方程在 Ω上进行积分，得到

调用恒等式(3)、式(4)以及利用ODE 常数变易法和能量守恒定律，再在(0,t)上进行积分，其中t∈[0,Tmax)，得到

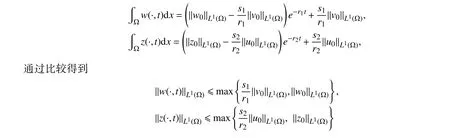
从而完成引理的证明。

接下来，我们回顾二维情形下的Gagliardo-Nirenberg 插值不等式[9]，这将用来证明我们的主要结果。

2 定理1 的证明