基于声源信号的GIL击穿性放电定位研究

马文长,马博辉,何宁辉,陈晨,尚彦军,刘博,陈巳阳

(1.国网宁夏电力有限公司检修公司，宁夏 银川 750011；2.四川大学电气工程学院，四川 成都 610065;3.国网宁夏电力有限公司电力科学研究院，宁夏 银川 750011)

气体绝缘金属全封闭输电线路(gas-insulated metal enclosed transmission line,GIL)作为一种安全可靠的输电方式，与传统的架空线及电力电缆相比，具有占地面积小、输电容量高、受电磁干扰小等优势。GIL中常见的缺陷有载流导体表面缺陷如金属毛刺、尖角等,在GIL生产、运送、安装过程中混入的金属微粒异物[1],绝缘体中的缺陷，如气泡、裂纹等易发生放电[2],绝缘气体中混入的水分会在固体绝缘材料表面凝露，形成闪络[3]。目前在GIL耐压试验中常用的击穿点定位方法有人工监听法、低频振动检测法、特高频检测法及超声波检测法等，均存在不足[4-7],而GIL在发生击穿性放电时会发出强烈声信号，且在传输过程中，中低频声信号的衰减速度远慢于超声波信号及超高频信号，通过声信号传感器检测击穿性放电的范围更大，更适合于GIL的狭长管道结构，对于工程中的实际应用具有重要意义。

1 GIL击穿性放电声场分布的仿真分析

为研究声信号在GIL中传播特性，得到故障声波在空气及GIL外壳中的传播途径、传播速度及传播中的衰减情况，本文基于声学基本方程建立了GIL基本单元的管道模型，并采用声学有限元法分析在点爆炸脉冲声源下GIL外壳表面的声场分布，为击穿性放电故障检测定位时的测点布置提供指导依据；同时研究声波在空气和GIL外壳中的传播特性和波形特征有助于寻找和确定更好的定位方法。

1.1 GIL声场分布数学模型

在进行GIL管道内声波传播规律分析时需要依据数学模型对GIL内声场分布进行数值求解，采用声学方法对GIL管道声场进行建模仿真，模型建立基础是数值声学的基本方程——Helmholtz波动方程，可通过声波的连续方程、运动方程和物态方程推得。

1.1.1 Helmholtz方程

声波的连续方程为

(1)

声波的运动方程为

(2)

声波的物态方程为

(3)

式中:ρ0、f0—静态情况下流体的密度和声压;

ρ′、f′、q′—外界扰动引起的流体密度、声压和速度的变化量;

γ—气体定压比热容与定容比热容之比。

由式(1)—式(3)可推得Helmholtz方程为

▽2f(x,y,z)-k2f(x,y,z)=-jρ0ωq(x,y,z)(4)

式中:k=ω/c,波数；

ω—角频率。

1.1.2 边界条件

声信号在GIL中传播时涉及到多种媒质，在媒质交接耦合处需依据声信号传播规律及媒质材料特性设置边界条件，以求更真实的仿真效果。

声波在由一种介质向另一种介质传播时会发生反射和折射现象，入射、反射与折射波的方向满足式(5)Snell定律：

(5)

式中:θl、θr、θt—声波在两种介质中的入射角、反射角和折射角;

c1、c2—两种介质中声音的传播速度。

声信号穿越两种不同介质时折射系数与反射系数如式(6)与式(7)所示：

t=2ρ2c2/(ρ2c2+ρ1c1)

(6)

r=(ρ2c2-ρ1c1)/(ρ2c2+ρ1c1)

(7)

在研究声场分布时采用有限长管道模拟无限长管道，计算声场分布时要求声信号在管道单元两端不发生反射，即要求GIL管道端部阻抗匹配，故在GIL两端参数设置时外加与相应媒质声特性阻抗值相同的阻抗[8]。式(8)所示为声传播介质的声阻抗定义：

Z=ρ·c

(8)

1.1.3 初始条件

在进行声场分布计算时，即在进行声学Helmholtz方程求解时，需首先确定起始条件，即施加的声激励波形及幅值。

1.2 基于LMS Virtual.Lab软件的GIL声场仿真

GIL通常采用SF6气体或SF6与N2的混合气体作为绝缘介质，主要由导体、外壳及支撑绝缘子等组成，其管道结构模型如图1所示。

图1 GIL管道结构模型

采用声学有限元法解Helmholtz方程，将所计算的声场V离散成一定数量的小声场，每个小声场称为单元，单元之间通过节点相连。对GIL管道基本单元中每一有限元应用Helmholtz方程，模拟爆炸声源声压级已知，可求出所在单元其他节点声压级，当前单元的节点输出为下一单元的节点输入，如此迭代可计算出场内各个点的声压级，得到GIL管道声场分布。在LMS Virtual. Lab软件中采用六面体有限元分隔GIL管道单元来研究GIL管道声场分布，如图2所示。

图2 有限元分隔GIL管道

由于声音在不同介质内传播速度不同，建立由SF6、GIL外壳及空气组成的三层耦合模型，其密度及传声速度参数如表1所示。

由表1可知,GIL管道外壳的密度及传播速度都远大于SF6中的相应值。由式(7)可知，反射系数r约等于1，声波从SF6气体入射到GIL壳内壁时几乎全部被反射。

1.3 声波在GIL上的传播特性

为模拟GIL发生击穿性故障时间短、强度大的声信号，在GIL一端轴心(输电导体)点施加爆炸脉冲信号激励，声压峰值为114 dB，如图3所示。

图3 声源激励波形

图4、图5分别为计时0.1 s及2.3 s时的GIL管道声场云图。分析可知，施加点声源后GIL中声波由三部分组成：一是沿直线在气体环境中传播的直达声，为平面波，传播过程中最先发生衰减且衰减速度较快，在18 m的传播距离内大约衰减30 dB，可通过GIL外壳透射到空气介质当中;二是反射声，声波从SF6气体到GIL外壳时反射系数接近1，爆炸声不断在气体绝缘环境中发生反射，此反射声为非平面波，在反射过程中不断衰减，该信号对于击穿性声信号定位意义及影响均不大;三是爆炸脉冲声源引起的管道振动发声，频率较低，持续时间长达数秒之久，类似敲钟后的嗡鸣。

图5 2.3 s时的GIL管道声场分布云图

图6为GIL管道的时域声压，橙色线为管外空气上某点的声压波形，蓝色为SF6气体某点声压波形。

图6 GIL管道的时域声压

通过对三种声波信号特征进行分析，直达声透射到空气部分的声波具有较明显的峰值，选择以该峰值为特征量估计不同传感器接收信号时延，采用时差定位法对声源进行定位。

2 声信号去噪方法

在进行现场声信号测量时由于人语及背景白噪声等干扰的存在，采集的声信号会混入噪声，这将对声信号的时延估计及基于声信号的故障定位产生干扰，为保证声源定位精度首先需要对声信号进行去噪处理。

2.1 结合小波的EMD去噪方法

小波变换(wavelet transform，WT)是一种能够进行时间频率局部化分析的变换方法，具有多分辨率的优点，通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分的效果能自动适应时频信号分析的要求[9]。小波变换用有限长的会衰减的小波基代替傅里叶变换中无限长的三角函数基，将小波基平移后再与待分析信号做内积。由于计算机只能处理离散化数据，离散小波变换定义如式(9)所示：

(9)

小波变换可等效为一组镜像滤波过程：将信号通过一组高通滤波器和一组低通滤波器，相当于将原始信号S分解为近似分量CA(低频量)和细节系数CD(高频量)，小波去噪即找出分解后由信号控制的小波系数并保留，剔除由干扰信号控制的小波系数，对保留下的小波系数进行重构得到去噪后的信号[10]。

经验模态分解算法(empirical mode decomposition,EMD)是一种新型自适应信号时频处理方法，特别适用于非线性非平稳信号的分析处理。在进行小波变换时需要提前选好基函数和尺度函数，而EMD算法依据数据自身的时间尺度特征来进行信号分解。在进行去噪时，根据不同的指标选取的本征模函数不同，重构后的去噪效果也就不同。本文提出一种结合小波的EMD去噪方法，具体做法如下：

(1)对原始信号进行EMD分解；

(2)计算各本征模函数分量与原信号相关系数并求其中最大值，将该值的1/10作为门槛值；

(3)对相关系数大于门槛值的本征模函数分量视为有用信号予以保留，其余予以剔除；

(4)对保留下来的本征模函数分量根据波形特征选择合适的小波基、分解层数及阈值进行小波去噪得到新的本征模函数分量；

(5)重构信号。

相比于没有结合小波的EMD去噪，此法优势在于能够适用各种不同信号，在对信号进行EMD分解后，不论有用信号和干扰信号如何分布，该法都能够有效地从中分离出噪声，得到有用信号。

2.2 仿真信号去噪结果

s(t)=e-10(t-0.08)sin 1000(t-0.08)

(10)

GIL的放电故障声信号频率约为400～1000 Hz，以式(10)所示函数作为仿真信号，对该信号加15 dB高斯白噪声进行去噪实验，信号波形如图7所示。

(a) 仿真信号

分别用小波阈值法、EMD法及结合小波的EMD法对去噪效果进行验证，如图8—图10所示。可以看出结合小波的EMD算法去噪效果最好，能够更彻底地滤去噪声干扰。

图8 小波阈值法去噪结果

图9 EMD法去噪结果

图10 结合小波的EMD法去噪结果

为更精确地比较不同方法的去噪效果，引入均方误差和信噪比两个量化指标，结果如表2所示。相较于小波阈值法和EMD算法，结合小波的EMD算法去噪均方误差最小为0.0 417，信噪比最高为13.376 4 dB，结合小波的EMD算法去噪性能最优。

表2 去噪后的均方误差及信噪比

2.3 实际声信号去噪结果

以敲击GIS管道的声信号进行去噪试验，声源信号如图11所示。

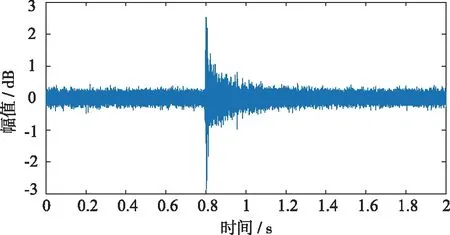
图11 敲击GIL管道声信号

时域波形呈振荡衰减状，其中混有幅值频域能量集中在400～2500 Hz，噪声干扰分布在各个频段，信号受回声和背景噪声干扰，存在多个尖峰凸起。运用结合小波的EMD算法对此实际含噪声信号进行去噪，结果如图12所示，可以看出去噪效果明显，计算得到信噪比可达5.748 5 dB。

图12 结合小波的EMD算法去噪效果

3 基于时差法的声源信号定位方法

声源定位即求出传感器到声源的距离，距离可由绝对时间与信号传播速度之积得到。对于GIL管道击穿性放电故障定位问题，由于无法得知故障发生准确时间，可基于时间差，使用多个传感器接收同一信号，根据各个传感器接收到信号的时间差与声速及传感器之间的距离等已知量求出声源位置。

3.1 信号时延估计方法

常见的信号时延估计方法有基本互相关法、广义互相关法、基于特征量的时延估计方法等，由于存在信号衰减及噪声干扰，远端传感器接收信号与近端传感器接收信号相比，时域长度较长、幅值较小、在噪声和回声干扰还可能出现多个尖峰值，由此进行估计得到的时延精度会下降甚至得到错误结果。在GIL发生击穿性故障时，声信号通过三种途径同时传播：

(1)通过GIL管道传播的振动发声；

(2)通过SF6气体直线传播的直达声；

(3)在SF6气体中来回反射传播的反射声。

由固体传播的振动声信号幅值较小但传播速度较快,最先被捕捉，随后通过SF6气体传播的幅值较大、速度较慢的声信号被捕捉。基于故障声信号特点，选取由管道内SF6气体传播的直达声信号的第一个上升沿作为特征量进行时延估计，其具有易于捕捉、特征稳定的优点。

3.2 实际声信号源定位实验

采用敲击GIS声信号定位实验作为基于声信号的GIL击穿性放电故障定位的代替实验，对管道不同位置进行敲击，并采用声传感器在确定位置接收敲击信号，分析信号并进行时延估计，进而求得声源位置，与敲击位置比对验证定位准确度。

实验现场布置如图13所示，实验部分管长3.3 m，声信号源定位采用直线定位法，基本定位单元需两个声信号传感器，共进行两组实验。

图13 敲击GIS实验现场布置

(1)如图14所示，传感器1、2相距1.65 m，且传感器连线与管道部分平行，为保证直线定位法的精度、减少理论误差，传感器高度与GIS管道中心轴等高为72.5 cm，与管道距离为20 cm。用金属小锤在与传感器1距离为0.415 m、0.825 m及1.235 m处分别进行敲击并记录信号波形，重复5次。

图14 敲击GIS实验一

应用结合小波的EMD算法对采集到的声信号进行降噪处理，随后提取特征量进行时延估计并完成定位，实验结果如表3所示。

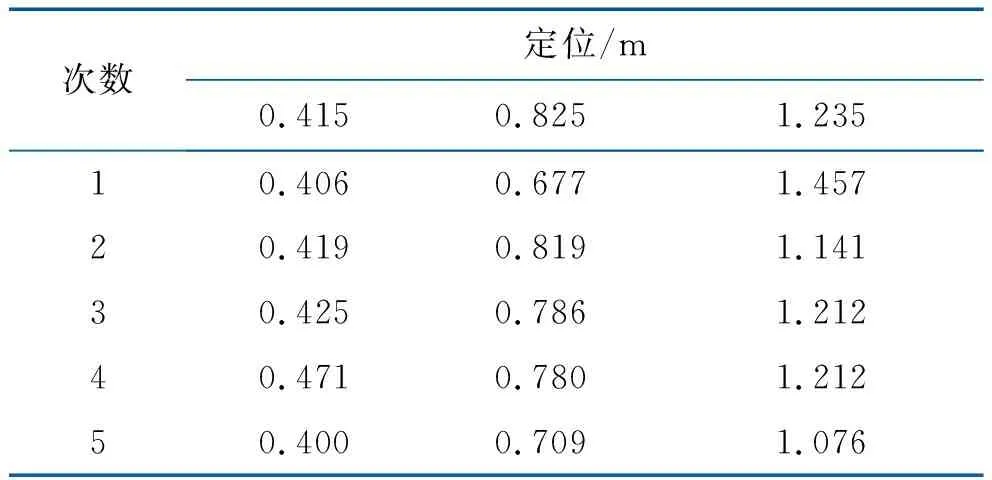
表3 实验一声源定位

(2)如图15所示，调整传感器1、2位置使其相距3.3 m。用金属小锤在与传感器1距离为0.825 m、1.650 m及2.475 m处分别进行敲击并记录信号波形，重复5次。

图15 敲击GIS实验二

应用结合小波的EMD算法对采集到的声信号进行降噪处理，随后提取特征量进行时延估计并完成定位，实验结果如表4所示。

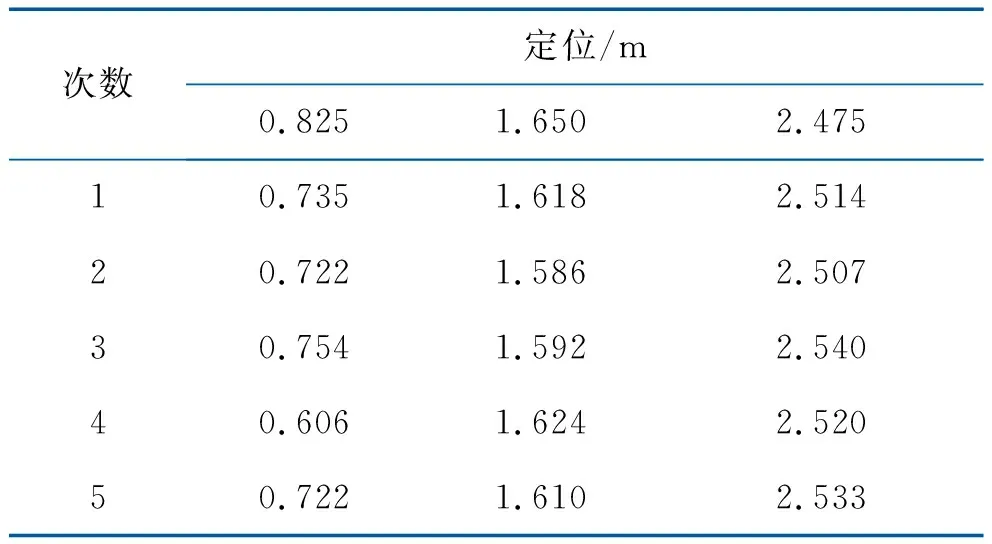
表4 实验二声源定位

在两组实验中共进行30次定位，其中23次定位误差在10 cm以内，28次定位误差在16 cm以内。只有两组数据定位误差达到 22 cm，总体定位精度较高。定位误差的直接来源是时延估计的误差，而时延估计误差来自以下两点：

(1)现场有其他突发声信号混入形成干扰；

(2)进行时延估计所选用的特征值首上升沿无法通过算法精确获得，在个别特殊情况下，首上升沿定位偏差较大从而导致时延估计出现误差，造成定位不够精准。

4 结 论

(1)在点爆炸脉冲声源激励下，GIL管道声波有三种方式传播：沿直线在介质中传播的直达声；介质中的反射声；GIL管道外壳的振动发声。其中直达声为平面波先发生衰减，在18 m的传播距离内约衰减30 dB。管道振动声频率低且持续时间长，可达数秒之久。

(2)直达声具有明显峰值且能够通过管道外壳透射到空气介质中，被声传感器捕获用于故障的检测和定位。

(3)提出一种结合小波的EMD算法去噪。以相关性为筛选指标选取对信号EMD分解后的特征模函数分量，进行小波阈值去噪后再重构。通过对仿真信号和实测信号的去噪结果分析，发现新方法提高了去噪后的信噪比、降低了均方误差，提升了去噪性能。

(4)以敲击GIS实验进行声源信号定位研究，基于两传感器的直线时差定位法，证明了将声信号用于GIL击穿性放电故障诊断中，可以实现故障点的精确定位。