基于改进平衡优化器的电力系统最优潮流计算

赵娟

(中国电力工程顾问集团西北电力设计院有限公司， 陕西 西安 710000)

最优潮流计算主要是通过调节电力系统可利用的控制变量来寻找能满足所有约束条件,使系统的某一性能指标达到最优值的潮流分布。由于最优潮流计算与电力系统的安全、稳定、经济运行密切相关，自20世纪六七十年代以来已有大量优化技术[1-7]被用于求解电力系统的最优潮流计算问题。早期电力系统的最优潮流主要通过经典的数学规划方法来求解，其优点在于计算速度快，缺点主要是求解结果较依赖于初值的选取和难以处理含离散变量的最优潮流计算问题。智能算法一般借助多个搜索代理来进行寻优，有效避免了初值选取不当带来的问题，计算精度一般较经典数学方法高，且无需求取梯度，能更好地处理含离散变量的最优潮流问题，其主要缺点在于每代均需计算并比较目标函数值以确定进化方向，计算成本较高。随着计算机计算能力和计算速度的不断提升，未来智能算法有望在求解最优潮流问题上得到更广泛的应用。

平衡优化器(equilibrium optimizer, EO)是Afshin Faramarzi等人于2019年提出的一种新型智能算法，并在多个测试函数上相对传统智能算法表现出较好的优越性[8]。平衡优化器自提出以来，现已在自动电压调节器控制参数优化[9]、肖特基二极管最优参数估计[10]、光伏参数估计[11]等多个工程领域得到了应用，且相比多个传统算法表现出了较好的优化性能。目前，平衡优化器在电力系统最优潮流计算中的应用仍较少，文献[12]将平衡优化器用于交直流混合电网的最优潮流计算问题，在发电成本、污染物排放、网损及电压偏移等四个目标上的计算表明，平衡优化器较差分进化算法、粒子群算法表现出了更好的优化性能。文献[13]将平衡优化器用于含高比例风光新能源电网的无功优化问题，并提出与遗传算法、粒子群算法、生物地理优化算法相比，平衡优化器能更快地收敛到更高质量的无功优化方案。文献[14]提出群智能算法的寻优过程可以分为搜索和利用两个阶段，搜索过程一般通过引入扰动变量等方式使得更新过程尽可能随机，以在整个搜索空间做全局性、大范围的寻优。利用过程侧重于在更新过程中发现的较有希望的部分区域进行细致寻优。生成概率(generation probability, GP)是平衡优化器中引导算法寻优过程的重要参数，文献[8]提出该参数设置为不同值时，会导致算法具有不同的搜索能力。该参数设置过小易使算法陷入局部最优，设置过大又将得到不精确的优化解，对该参数的灵敏度分析表明，其设置为0.5时算法可以较好平衡其搜索和利用的能力，从而可获得更好的寻优效果。目前包括文献[12]和文献[13]在内的多数文献均采用该设置,但将生成概率取为常数会存在难以灵活地平衡及控制算法搜索和利用能力的缺点，因此，本文提出一种基于自适应生成概率的改进平衡优化器(modified equilibrium optimizer, MEO)，通过与原平衡优化器以及粒子群算法在求解IEEE118节点系统最优潮流问题上的对比，发现改进算法表现出了相对更好的寻优性能。

1 数学模型

1.1 目标函数

1.1.1 系统网损

电力系统网损可表示为

(1)

式中:N—系统中的节点总数；

Gij—节点i和节点j之间的线路电导；

Ui和Uj—节点i、j处的电压；

θij—节点i、j之间的相角差。

1.1.2 电压偏移

电压偏移的计算公式为

(2)

NB—负荷节点个数。

1.1.3 发电成本

发电机的发电(燃料)成本可表述为

(3)

式中:ai、bi和ci—发电机i的成本系数；

NG—发电机节点数；

使用罚函数项处理状态变量的不等式约束，将需要优化的目标值J表示如下：

(4)

式中:

(5)

(6)

式中:fk—原求解目标；

ηU和ηQ—负荷节点电压和发电机无功出力越限的惩罚系数；

ΔUi和ΔQj—负荷节点电压和发电机无功出力越限的惩罚项。

1.2 等式约束

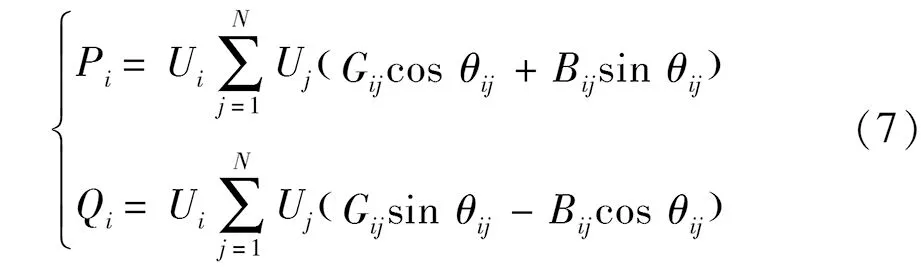
式中:Pi、Qi—节点i、j注入的有功和无功功率；

Bij—节点i、j之间的线路电纳。

1.3 不等式约束

控制变量的不等式约束包括:

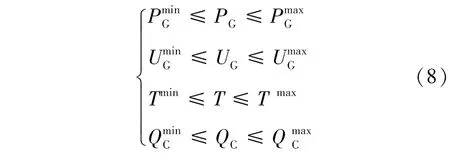
式中：PG、UG、T、QC—发电机有功出力、机端电压、变压器变比、并联电容器补偿容量；

max、min—变量的上下限。

状态变量的不等式约束包括:

(9)

式中:UB、QG—负荷节点的电压和发电机的无功出力。

2 平衡优化器及其改进

2.1 算法物理学背景

平衡优化器是受到物理学中的质量平衡方程的启发而提出的一种新型智能算法。质量平衡方程描述了质量在一个控制容积内进入、离开和产生的过程，可用一阶微分方程表示为

(10)

式中：V—控制容积；

C—控制容积内的浓度；

Q—流进或流出控制容积的容积流速；

Ceq—控制容积处于平衡状态时的浓度；

G—控制容积内的质量生成速率；

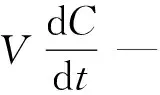
(11)

设t0和C0分别为初始的时间和浓度值，对式(11)两边同时积分得：

(12)

求解式(12)可得：

(13)

式中:F=exp(-λ(t-t0))。

2.2 算法模型

2.2.1 初始化

与多数启发式算法类似，平衡优化器的初始化过程可以表述为

(14)

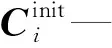
Cmin和Cmax—个体的下限和上限向量；

randi—[0,1]之间的随机向量；

n—种群中的个体数。

2.2.2 建立平衡池

平衡状态是算法收敛到的最终状态，在优化过程中，平衡池的作用在于为整个寻优过程提供候选解。由当前初始化/迭代过程所产生的适应度值相对最优的4个个体及其平均值构成平衡池：

(15)

平衡池中的5个个体被选中作为引导优化过程的解的概率是一样的，即均为0.2。

2.2.3 指数项

指数项是算法更新过程中的重要组成部分，可表示为

(16)

变量t被定义为一个随着迭代次数递减的函数，即：

(17)

式中:Iter和Max_iter—当前迭代次数和最大迭代次数；

a2—常数，一般取1。

为确保算法收敛，同时提高算法搜索和利用的能力，考虑：

(18)

式中:a1—常数，一般取2；

sign —数学符号函数；

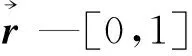
将式(18)带入式(16)，可得：

(19)

2.2.4 生成速率

算法生成速率定义为一个一阶指数衰减过程：

(20)

为得到一个更加可控和系统的搜索模式，算法中设置k=λ，并引入之前导出的指数项，将生成速率描述为

(21)

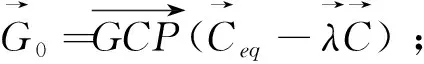
(22)

r1和r2—[0,1]之间的随机数;

GP—生成概率，一般取0.5。

综上，平衡优化器的最终更新公式被定义为

(23)

式中:V值— 一般取为常数1。

在式(23)中:第一项为平衡状态下的浓度；第二项和第三项表征浓度的变化，其中第二项贡献算法的搜索能力，会引起个体在平衡态附近的剧烈变化;第三项则贡献了利用能力，通过小的浓度变化使所求得的解更为精确。

2.2.5 个体记忆保存

参照粒子群算法中个体最优的概念，平衡优化器建立了个体记忆保存机制，在第Iter(Iter≥2)次迭代后，每个个体求得的适应度值将与第Iter-1次迭代后所求得适应度值进行比较，若第Iter次迭代后个体求得适应度值更好，则将个体位置和适应度值进行相应的更新，反之则不做更新，并维持第Iter-1次迭代后求得的个体位置和适应度值进入下一次迭代。该机制主要是为了提高算法的利用能力。

2.3 算法改进

文献[8]提出，生成概率是影响算法搜索能力的重要参数，该参数设置过小易使算法陷入局部最优，设置过大又将得到不精确的优化解，对该参数的灵敏度分析表明，其值设置为0.5时算法可以较好平衡其搜索和利用的能力，从而获得更好的寻优效果。为通过生成概率更好的平衡算法的搜索和利用过程，本文考虑将生成概率进行自适应取值，即设置生成概率为

(24)

生成概率随迭代次数的变化趋势如图1所示。

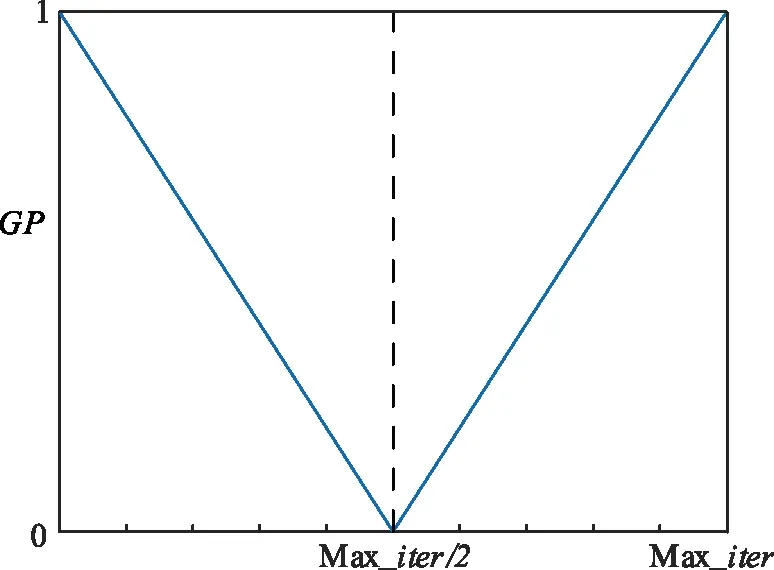
图1 生成概率随迭代次数的变化曲线

由图1可见：在迭代过程初期，生成概率较大，可以使得算法侧重于进行可行域内的大范围搜索；随后生成概率逐渐减小，到迭代过程进行到一半变为0，算法侧重于在局部范围进行细致搜索并得以逐渐收敛；然后生成概率又重新增大，并在迭代结束时重新取到最大值1，这有利于增加算法在寻优后期的种群多样性，不至于在寻优后期因种群趋同而陷入局部最优。

2.4 算法流程

(1)初始化种群及参数。按照式(14)对种群进行初始化，设置算法所需参数a1、a2、V和GP，确定种群规模和最大迭代次数；

(2)对种群中的个体进行潮流计算得到所有个体的适应度值，并进行个体记忆保存操作(Iter≥2)，根据个体适应度值的大小选择4个个体，并计算这4个个体的平均值，从而建立平衡池；

(3)根据当前迭代次数，按照式(19)计算算法指数项。由式(24)计算生成概率，并按照式(21)计算算法生成速率；

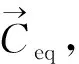
(5)检查当前迭代次数是否为最大迭代次数，若否则继续重复步骤(2)—(4)，若是则退出迭代，并取平衡池中的最优个体为最终的优化解。

3 算例分析

本文所用算例为IEEE118节点系统[15]，该系统包括54台发电机，186条线路和9台变压器。取负荷节点电压的上下限约束为[0.95,1.1]，电压越限的罚因子取为1000，不约束发电机无功[16]，该算例初始惩罚项为4.580。控制变量取值如下：

(1)发电机有功出力。除69号机为平衡机外，其他53台发电机的上下限按初始值的±20 MW取值，如果±20 MW后超过了对应的上下限，则取为规定的上下限值。

(2)发电机机端电压在[0.95,1.1]范围内连续调节。

(3)变压器变比在[0.9,1.1]之间分16档，进行分档调节。

使用平衡优化器(EO)、粒子群算法(PSO)及改进平衡优化器(MEO)分别对IEEE118节点系统的网损、电压偏移和发电成本进行计算，设置各算法种群规模为40，迭代次数为1000。粒子群算法参数按照文献[17]取为c1=c2=2,w=1。

3.1 系统网损

IEEE118节点系统初始系统网损为132.863 MW。三种算法对IEEE118节点系统的网损目标值优化结果见表1，不同算法求解网损目标平均值的迭代曲线见图2。

图2 三种算法求解网损目标平均值的迭代曲线对比

表1 三种算法求得的IEEE118节点系统网损目标值

3.2 电压偏移

IEEE118节点系统初始电压偏移为1.439。三种算法对IEEE118节点系统的电压偏移目标值优化结果见表2，不同算法求解电压偏移目标平均值的迭代曲线见图3。

表2 三种算法求得的IEEE118节点系统电压偏移目标值

图3 三种算法求解电压偏移目标平均值的迭代曲线对比

3.3 发电成本

图4 三种算法求解发电成本目标值的迭代曲线对比

表3 三种算法求得的IEEE118节点系统发电成本目标值

由以上IEEE118节点系统的最优潮流计算结果可见，改进平衡优化器和平衡优化器计算结果的标准差更小，计算鲁棒性优于粒子群算法；同时改进平衡优化器相较平衡优化器以及粒子群算法，计算结果平均值更小，计算性能具有明显进步，在网损、电压偏移和发电成本3个目标上均取得了最好的计算效果。

4 结 论

为克服原平衡优化器将生成概率取为常数带来的难以平衡搜索和利用过程的缺点，本文提出一种基于自适应生成概率的改进平衡优化器，并将其用于IEEE118节点系统的最优潮流计算问题，通过与原平衡优化器与粒子群算法在系统网损、电压偏移和发电成本3个目标上进行对比，结果表明改进算法表现出了相对更好的寻优性能，是一种很有潜力的优化算法。