基于快速运动场景下的目标跟踪改进算法
瑚 琦,查彤彤,李 锐
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.上海理工大学 上海市现代光学系统重点实验室,上海 200093)
引 言
目标跟踪作为计算机视觉研究的一个重要课题,在交通巡逻[1]、自动驾驶[2]、智能人机交互[3]等众多领域中具有重要作用。尽管已有大量的研究成果,但是仍存在如快速运动、尺度变化和遮挡等亟待解决的问题[4]。由于相关滤波对于外界光照的敏感性以及目标自身的几何变化具有高效的计算能力和优越的鲁棒性,所以相关滤波在目标跟踪领域具有广泛的应用性。
Bolme等[5]将相关滤波应用于目标跟踪领域,通过计算目标和待测样本之间的信号相关性,对下一帧的目标位置进行判定。2014年,Henriques等[6]将高斯非线性核函数引入相关滤波,实现基于核相关滤波的高速跟踪。Danelljan等[7]引入尺度变换的概念,实现跟踪过程中的尺度自适应。Bertinetto等[8]提出将颜色特征[9](Color)和梯度直方图特征[10](HOG)按照一定比例的融合互补,从而提升目标运动过程中针对形变、光照等问题的鲁棒性。Danelljan等[11-12]使用连续的卷积滤波器并对特征图进行降维。在维持跟踪速度的同时,提高了跟踪效果。Galoogahi等[13]使用真实移位产生的负样本作为背景信息,有效抑制了边界效应,同时提出了一种基于ADMM[14](交替方向乘子法)的优化方法,降低了计算量从而提升了跟踪速度。Li等[15]提出了Autotrack(automatic spatio-temporal regularization)算法,该算法引入自适应时空正则项,有效提升了跟踪速度。以上算法针对目标跟踪存在的问题分别做出了不同的改进,但边界效应和滤波器退化,始终影响跟踪器在应对快速运动以及遮挡等复杂场景问题时的性能。其中Autotrack虽然提升了跟踪速度,但其在快速运动情景下的目标跟踪表现较为乏力。
当目标快速运动时,会造成目标信息的丢失,使得目标跟踪的准确率大幅度下降。本文在Autotrack的基础上,提出基于快速运动场景下的目标跟踪改进算法。该方法在目标发生快速运动的场景下,可有效提升跟踪器在面对快速运动等不利于跟踪时的稳定性。本文主要工作如下:1)通过引入空间正则项,获取空间正则权重,利用相邻两帧响应图的隐藏联系作为时间正则项,使其在跟踪过程中自适应更新,在避免滤波器退化的同时可以有效缓解边界效应。2)将空间正则项与时间正则项相结合引入目标函数中对滤波器进行约束,提升跟踪性能。3)经改进后的算法使用ADMM对目标函数进行优化,基本可以实现实时跟踪。
1 本文算法
Autotrack跟踪算法是将引入的相邻两帧响应联系作为自适应时空正则项,以使滤波器专注于对象的可信赖部分的学习,同时可以确定滤波器的更新率,从而提高跟踪性能。但该算法的正则项部分仅仅依赖于相邻两帧的响应图联系,在针对快速运动场景下的目标跟踪时,表现较为乏力,当目标快速运动时,会丢失有效的跟踪信息。本文在Autotrack算法的基础上,引入空间正则权重项w,对距离目标中心比较远的样本进行相应的惩罚,由此所得到的相关响应在目标背景处的值得到了明显的抑制,从而有效缓解边界效应。将相邻两帧全局响应图变化量作为时间正则项,使其在解决边界效应的同时有效地抑制畸变,从而提升跟踪器在应对快速运动场景下的鲁棒性。提出目标函数为

式中:K表示通道总数;表示从第t个训练样本中提取的向量化后的第j个通道的特征;T表示xjt向量化后的长度;分别表示第t个训练样本以及第t-1 个训练样本在j通道的滤波器;y∈RT×1表示理想的高斯型输出; * 表示卷积操作; ∂t、 ∂ 分别表示沿用Autotrack算法中的时间正则项系数的相关值与优化值。

式中:符号 ˆ 表示对应物理量的离散傅里叶正变换(DFT);F表示求DFT系数矩阵; s.t.表示约束条件;Gˆt表示辅助变量。

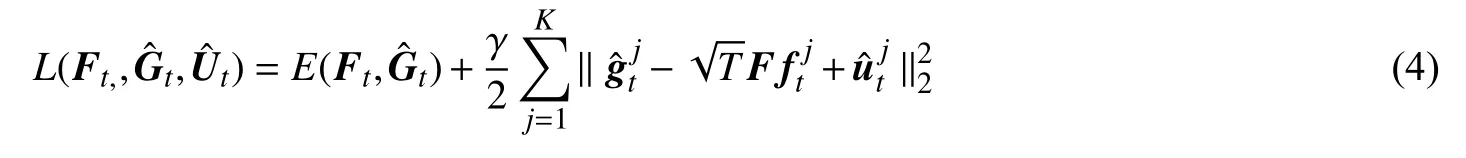
则式(4)可分为下列3个子问题进行求解, 即:

直接对该等式求导计算量过大,难以实现实时目标跟踪,因而对每个像素点通道的样本特 征进行采样,可将等式简化为,即
现引入Sherman-Morrison定理减少最优解 的复杂度,即有
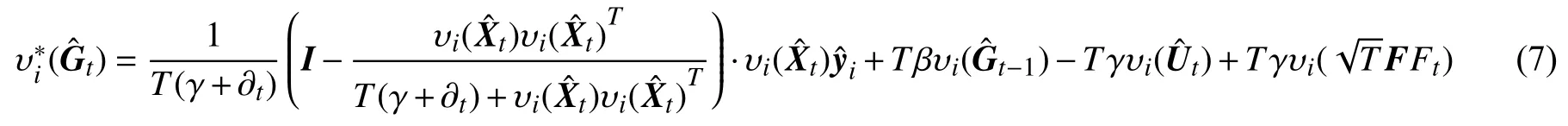
2)子问题
由矩阵的二范数和求导法则可知其闭式解为

式中A=diag(w)∈ RT×T,
3)子问题αt
解法同子问题 2)

4)子问题Uˆk+1
该求解过程实质上是对拉格朗日算子的更新,即
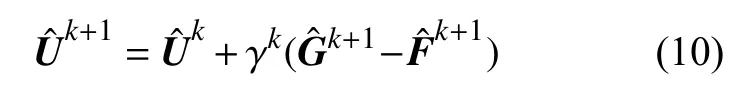
与是当前子问题的解,k表示优化技巧ADMM算法当前的迭代次数。
在算法的整个优化过程中,将滤波器和时间正则化参数的求解分成两个部分。第一部分是通过式(7)获得辅助变量频域解,再利用所得的辅助变量的值代入式(9)中,求出时间化正则参数 ∂t。第二部分是将辅助变量频域解的值代入式(8)中,求出最后的滤波器fj,即计算出具有最佳响应的滤波器。

通过式(5)获得t-1个样本在第j通道的辅助变量频域解,将其与下一帧样本的频域形式相乘,并将其结果转换至时域求得响应图Rt,即

将全部通道的响应图进行叠加,通过寻找响应图Rt中的最大值位置将其作为目标估计位置。
2 算法流程
本文算法的流程如图1所示。首先根据第一帧目标所在的位置,提取感兴趣区域的特征作为训练样本。本文引入空间正则项获取可靠的滤波器惩罚系数,相邻两帧的响应图联系作为时间正则项控制滤波器的更新,将两者相结合实现对滤波器的合理约束。使用相关滤波方法训练目标滤波器模板,在下一帧图像目标范围提取目标特征,构建尺度金字塔,估计出最优尺度模板并更新。采用自适应更新策略机制对目标响应峰值位置进行置信度判断并对模板进行自适应更新。

图1 本文算法流程图Fig.1 Flowchart of the algorithm in this paper
3 实验设置
为保证算法的公平性,本文所有实验均使用Hog特征,与基准Autotrack算法所提取目标的特征一致。本文实验均在2.50 GHz,Intel(R)Xeon(R)CPU, 32 GB RAM计算机上进行。
4 实验结果分析
为检验快速运动情形下的相关滤波跟踪算法的跟踪性能,本文选取8个相关滤波跟踪算法(Autotrack[14]、STRCF[16]、Staple[10]、FDSST[17]、KCF[6]、 Struck[18]、 CSK[19]、 TLD[20]) 在 OTB-2013数据集上与本文算法进行比较。OTB-2013公开数据集包括了快速运动、遮挡、低分辨率等各种挑战场景,因此常用于目标跟踪算法的综合性能评价标准。图2是不同跟踪算法在OTB-2013数据集上的距离精度曲线和成功率曲线。由图2可知,在快速运动场景下,本文算法的准确率和成功率名列前茅。改进后的算法添加了空间正则项,有效缓解了边界效应,提升了原算法在快速运动场景下的跟踪性能,相较于原基准Autotrack算法,得分分别上升了4.3%和2.6%。
图3是多种算法基于OTB-2013平台综合准确率和成功率图,其值如表1所示。经对比可知,本文提出的算法在综合得分上略有下降,准确率和成功率分别下降了1.3%和1.1%。经分析可知,其原因在于修改后的算法去除了原基准算法中局部响应变化项对滤波器的约束作用,尽管该算法使得跟踪器在快速运动的情景下实现了较好的跟踪性能,但是其抗遮挡能力不可避免地下降,因而影响了总体得分。

图2 多种算法基于OTB-2013平台快速运动场景下的准确率和成功率图Fig.2 Accuracy and success rates of algorithms based on OTB-2013 in fast motion scenarios

图3 多种算法基于OTB-2013平台综合准确率和成功率图Fig.3 Integrated accuracy and success rates of algorithms based on OTB-2013

表1 多种算法基于OTB-2013平台综合准确率和成功率Tab.1 Integrated accuracy and success rates of algorithms based on OTB-2013
图4、图5是多种算法基于OTB-2013平台于在低分辨率场景和出视野场景下的准确率和成功率图,相应的值如表2、表3所示。由此可知:在低分辨率的场景下,本文算法相较于STRCF算法,在准确率和成功率的得分上分别提升了14.5%和13.4%;在出视野的场景下,准确率和成功率分别提升了7.8%和5.8%。

图4 多种算法基于OTB-2013平台于低分辨率场景下的准确率和成功率图Fig.4 Accuracy and success rates of algorithms based on OTB-2013 in low resolution scenarios
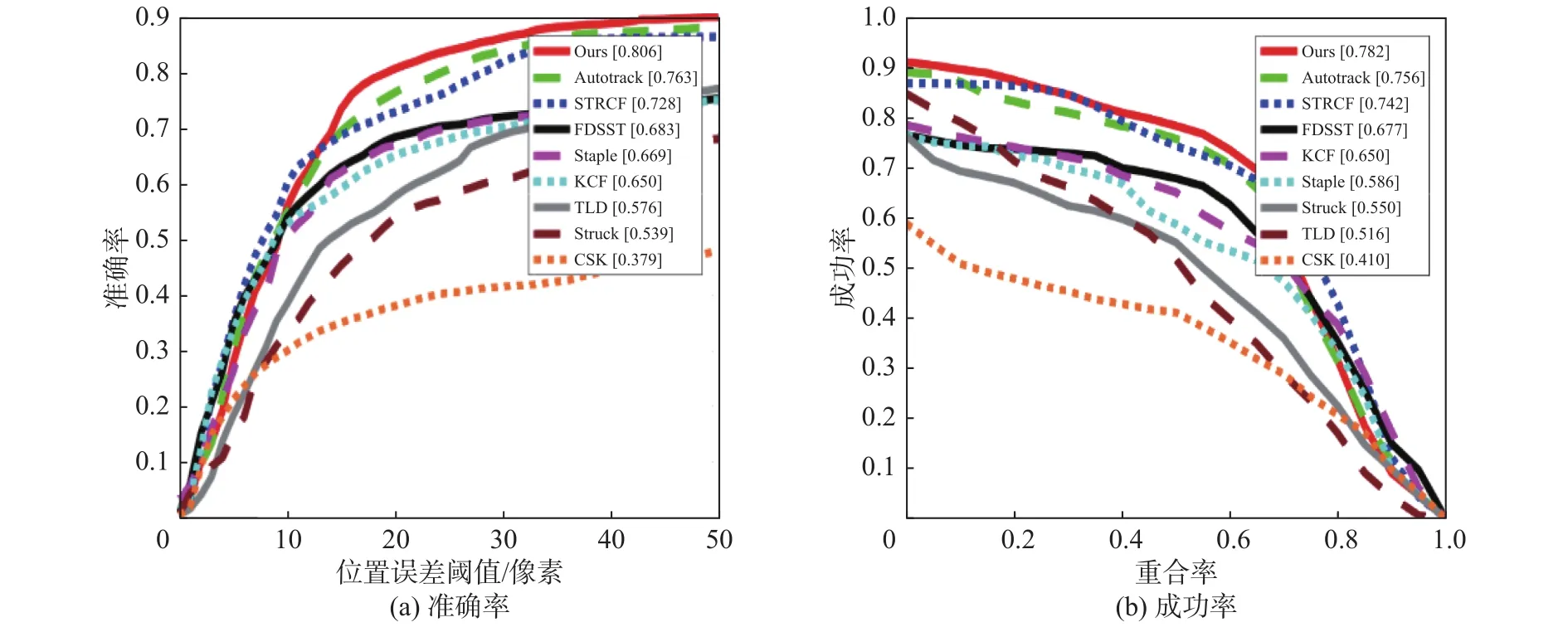
图5 多种算法基于OTB-2013平台出视野场景下的准确率和成功率图Fig.5 Accuracy and success rates of algorithms based on OTB-2013 in out of view scenarios

表2 多种算法在不同应用场景的准确率Tab.2 Accuracy of multiple algorithms in different application scenarios

表3 多种算法在不同应用场景下的成功率Tab.3 Success rate of multiple algorithms in different application scenarios
5 结 论
本文提出了将空间正则项与时间正则项相结合引入目标函数中进行优化的算法。通过引入空间正则项使空间正则权重在跟踪过程中与目标建立联系,从而获取可靠的滤波器惩罚系数。利用相邻两帧响应图的联系作为时间正则项,使其在跟踪过程中自适应更新,降低滤波器退化带来的影响,有效缓解边界效应。同时对跟踪过程中由于特殊场景导致的畸变进行抑制,提升跟踪器在应对快速运动等复杂场景时的鲁棒性。改进后的针对快速运动情景的算法,仍可用ADMM对目标函数进行优化,且不增加计算复杂度,基本可以实现实时跟踪。实验对比表明,在目标发生快速运动、低分辨率、出视野等复杂场景下,本文算法具有更强的稳定性。本文提出的算法在遮挡情景下仍有一定的提升空间,还可继续改进算法在应对遮挡情景下的鲁棒性,从而进一步提高跟踪性能。

