基于OPTIMUS的小型战术导弹多学科设计优化①
苏明慧,任全彬,罗志清,韩 飞,龚学兵,张 菲,张佩俊,张 熙
(1.中国航天科技集团有限公司四院四十一所,西安 710025;2.中国航天科技集团有限公司第四研究院,西安 710025)
0 引言
小型战术导弹命中精度高、机动能力强,是地面部队的重要武器之一。导弹总体设计作为一项复杂的系统工程,具有涉及的学科领域多、专业分工细、学科间耦合关系复杂和整体性能非线性的特点。如何从系统角度综合考虑多个学科的影响,有效组织和利用各种先进的信息化技术对导弹进行建模、仿真、分析以及优化,提高导弹的设计开发水平,是目前导弹设计领域亟须解决的问题之一[1]。多学科设计优化(Multidisciplinary Design Optimization, MDO)就此应运而生。MDO最早由Sobieski[2]提出,其以系统最优为目标,通过协调各学科(子系统)之间的耦合关系及优化过程,可获得系统最优的设计方案。在方案论证阶段,MDO技术具有较强的工程应用价值,有助于降低研制费用,缩短设计周期。
国外已经将MDO理论成功用于航空航天领域的工程实践。波音公司开发了基于高精度分析模型的飞机 MDO 系统——MDOPT[3]。美国喷气推进实验室在火星探测器的设计中运用了多学科设计优化技术[4]。NASA 开发了高拟真度MDO设计与优化工具Open MDAO[5-6]。国内也在导弹、运载火箭、有翼再入飞行器、亚轨道重复使用运载器和高超声速飞行器[7-15]优化设计与MDO技术的结合上做了一定的研究工作,但尚未成熟地用于工程实践。OPTIMUS是一款过程集成与多学科优化软件,可“设计、修改、再分析”流程自动化。OPTIMUS已经被广泛用于导弹总体参数设计[16]、导弹控制系统参数优化[17]、临近空间飞行器的再入轨迹优化[18]等方面。
本文依据某近程小型战术导弹总体设计问题,基于OPTIMUS研究MDO在导弹总体参数方案设计中的应用,旨在为提高导弹总体设计水平提供方法指导。
1 小型战术导弹多学科分析模型
1.1 小型战术导弹基准方案及系统分解
以某小型战术导弹总体设计方案为基准,假设导弹车载发射,发射俯仰角30°,发射速度30 m/s。导弹外形方案如图1所示。

图1 小型战术导弹外形方案
采用正常式布局,弹翼、舵翼“X”布局,弹长2.5 m,翼展1.2 m,舵展0.464 m。导弹推进方案为双脉冲固体火箭发动机,任务射程要求不小于30 km。其飞行任务剖面可分为爬升段、平飞段、攻击段,如图2所示。
导弹总体设计优化的主要任务是对导弹的设计参数进行寻优,以获得满足战术技术指标和设计限制条件的最佳设计方案[19]。导弹的总体性能主要由射程、速度、弹道、威力等决定。战斗部威力是方案论证中最先确定的战术技术指标之一,在工程实际中优化空间有限,故不将战斗部作为本文的子系统之一。
本文将小型战术导弹系统分解为推进、几何外形、气动、质量、弹道五个子系统,以此建立多学科总体优化模型。
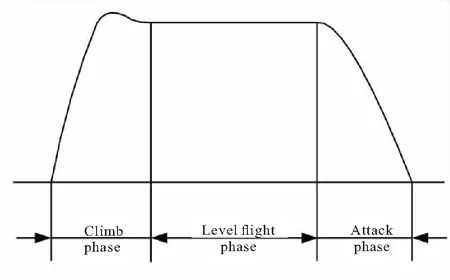
图2 飞行任务剖面图
1.2 小型战术导弹参数化学科分析模型
1.2.1 推进学科分析模型
推进学科分析模型以双脉冲固体火箭发动机为基准。发动机第一段推力使导弹在较短的时间内增速,第二段推力为导弹平飞提供推力,由控制系统操纵每段装药的点火时间。通过合理设计两段推力分配和点火延迟时间,可实现能量的有效利用。
在总体方案论证阶段,推进学科的任务是提出推力-时间曲线F(t)和质量-时间曲线m(t),受关注的参数主要有总冲、比冲、质量比、每段推力、推力工作时间、点火延迟时间等,详细的发动机设计在学科设计阶段进行。推进学科计算模型如式(1)所示:
It=F1t1+F2t2
(1)
式中It为发动机总冲;F1为第一段推力;t1为第一段推力工作时间;F2为第二段推力;t2为第二段推力工作时间。
mp=It/Isp
(2)
式中mp为发动机推进剂装药质量;Isp为发动机比冲。
mf=mp/μ
(3)
式中mf为发动机质量;μ为发动机质量比。
1.2.2 几何外形分析模型
依据基准方案,认为导弹壳体壁厚均匀,将弹翼位置、弹翼翼展、弹翼翼弦、尾翼位置、尾翼翼展和尾翼翼弦作为设计变量。战斗部威力与弹体直径正相关,威力指标确定后,弹体直径随之确定。弹体长度由引导头、仪器舱、舵机等制导控制部件长度和战斗部舱长度、发动机长度等确定,是一个间接设计变量。
1.2.3 气动学科分析模型
气动学科分析模型采用气动力工程估算软件 MISSLE DATCOM 进行气动力系数的计算。MISSLE DATCOM采用了部件组合法、模块化法(数据模块化和方法模块化),具有较强适应性和较高精度[20]。本文根据小型战术导弹基准方案与几何外形模型,建立了攻角、马赫数与气动力系数的二维插值表。图3为导弹基准方案的气动力系数插值图像。
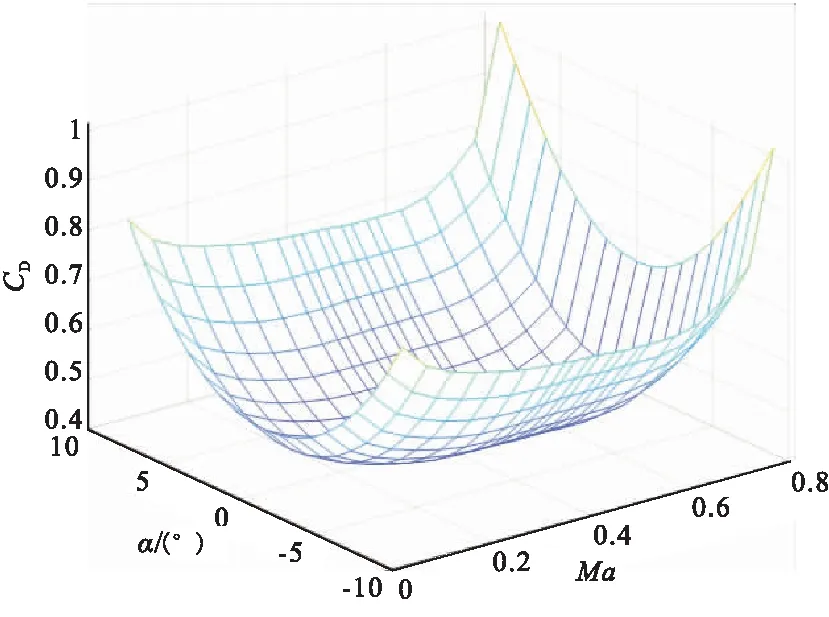
··(a)Drag coefficient interpolation image
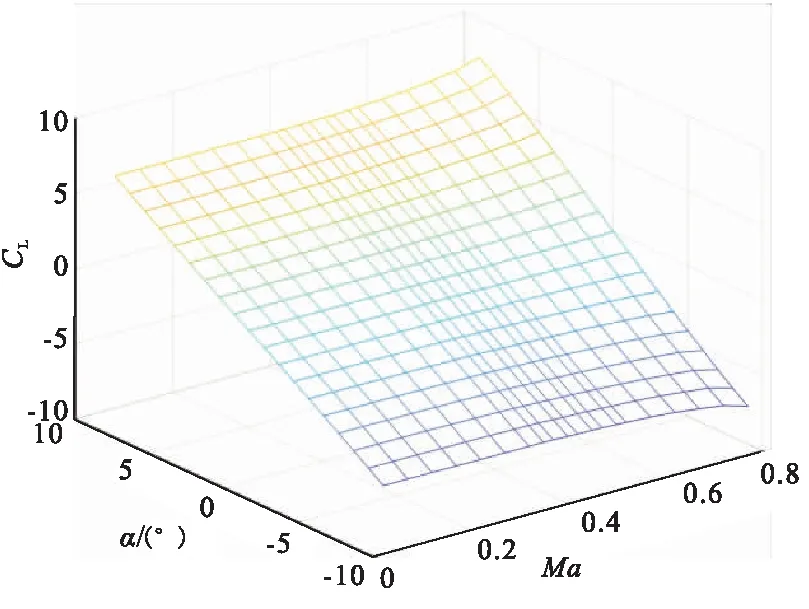
··(b)Lift coefficient interpolation image
1.2.4 质量学科分析模型
在总体方案论证前期,导引头舱、战斗部舱、舵机舱等选取相似型号的产品,认为其质量特性已知。本文主要针对发动机和弹翼、舵翼的质量进行优化设计。
质量学科分析模型采用简化的工程估算方法以降低优化模型的复杂度。根据导出型质量方程[21],可将导弹质量划分为有效载荷质量、发动机结构质量、发动机推进剂装药质量和弹翼、尾翼、控制机构等质量。其中,发动机结构质量和发动机推进剂装药质量由推进学科计算获得,进而得到全弹满载、半载、空载的质量特性。本文有效载荷与控制机构的质量固定。弹翼、尾翼初始质量由ProE计算得到,估算时认为其质量与翼弦、翼展的长度成正比。
m0=me+men+mp+ms
(4)
式中m0为导弹起飞质量;me为有效载荷质量;men为发动机结构质量;mp为发动机推进剂装药质量;ms为弹翼、尾翼、控制机构等质量。
1.2.5 弹道学科分析模型
弹道学科分析模型将导弹视为质点,以三自由度弹道方程组[22]进行弹道解算。由于技术指标要求的射程较近,可忽略地球自转对重力加速度的影响。考虑到在方案论证阶段应当给予攻角规律较大的设计空间,本文在优化时将攻角曲线离散成6个特征点作为设计变量,再以三次Hermite插值得到每个时刻的攻角数值。
2 小型战术导弹多学科总体优化模型
2.1 单目标优化问题
2.1.1 目标函数
导弹质量是总体方案论证阶段的重要战术技术指标,故选择射程一定前提下的导弹起飞质量最小为目标函数。
2.1.2 设计变量
本优化问题选择的设计变量有推进学科选择第一段推力F1、第二段推力F2、第一段推力工作时间t1、第二段推力工作时间t2、两段推力时间间隔tj;几何外形学科选择半翼展lw1/2、翼弦b1、弹翼轴向位置xle1、尾翼半翼展lw2/2、尾翼翼弦b2、尾翼轴向位置xle2;弹道学科选择攻角曲线特征点αi(t),i=1,2,…,6。
2.1.3 约束条件
本优化问题的约束条件如下:
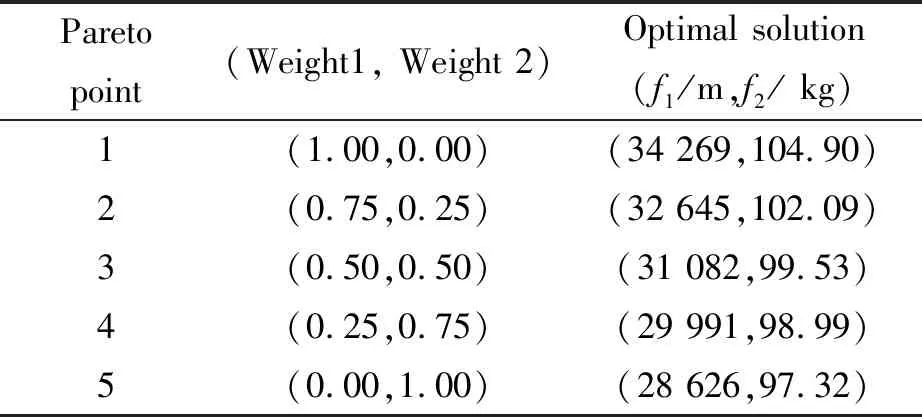
(1)射程约束:Rmin (2)尾翼轴向位置与尾翼弦长之和应小于弹身长度:xle2+b2 (3)平飞段高度H约束:Hmin (4)过载约束:nx (5)飞行马赫数Ma约束:Ma 2.1.4 优化问题模型 综上,单目标优化问题中设计变量17个,约束条件7个,数学表达式为 minm0=f(X) s.t.g1(X)=Rmin-R≤0 g2(X)=xle2+b2-LB≤0 g3(X)=H-Hmax≤0 g4(X)=Hmin-H≤0 g5(X)=nx-nxmax≤0 g6(X)=ny-nymax≤0 g7(X)=Ma-Mamax≤0 (5) 式中X=(F1,F2,t1,t2,tj,lw1/2,b1,xle1,lw2/2,b2,xle2,αi(t)),i=1,2,…,6。 2.2.1 目标函数 为探究导弹射程与起飞质量的耦合关系,选择导弹射程最大与导弹起飞质量最小为目标函数。 2.2.2 设计变量 为便于比较单目标优化与多目标优化的结果,本优化问题设计变量同单目标优化问题的设计变量。 2.2.3 约束条件 本优化问题约束条件同2.1.3节单目标优化问题的约束条件(2)~(5)。 2.2.4 优化问题模型 多目标优化问题中目标函数2个,设计变量17个,约束条件6个,数学表达式为 maxR=f1(X) minm0=f2(X) s.t.g1(X)=xle2+b2-LB≤0 g2(X)=H-Hmax≤0 g3(X)=Hmin-H≤0 g4(X)=nx-nx max≤0 g5(X)=ny-ny max≤0 g6(X)=Ma-Mamax≤0 (6) 通过分析小型战术导弹各学科间的耦合关系,可得其设计结构矩阵(Design Structure Matrix, DSM)如图4所示。图4中,对角线上的方框代表各学科分析模型,右上方区域表示数据的前馈传递,左下方区域表示数据的反馈传递。设计结构矩阵是多学科集成的基础。 图4 小型战术导弹设计结构矩阵 MDO优化过程(MDO Procedure)也称MDO算法或MDO策略,是MDO问题的数学表述及这种表述在计算环境中如何实现的过程组织[23]。 MDO优化过程按照优化器的数目可分为单级优化过程和多级优化过程。单级优化过程中优化器只存在于系统级,学科级则负责学科的分析与计算。常见的单级优化过程有多学科可行法(Multi-Disciplinary Feasible,MDF)和单学科可行法(Individual Discipline Feasible,IDF)。多级优化过程的系统级与学科级都存在优化器。其将系统优化问题分解为多个子系统的优化协调问题,各个学科子系统分别进行优化,并通过某种机制进行协调[23]。常见的多级优化过程有并行子空间优化(Concurrent Sub Space Optimization,CSSO)和协同优化(Collaborative Optimization,CO)。 常见MDO优化过程核心思想与优缺点总结归纳见表1。本优化问题的学科模型均应用工程估算方法,体现不出代理模型的引入在降低计算复杂度上的优势,故没有必要选择CSSO 优化过程。系统级和气动学科(气动子系统级)之间的数据传递在工程上实现复杂,故不采用CO优化过程。由于多级优化过程的收敛性尚未被证明,采用多级优化过程还会出现优化效率下降与优化结果精度降低的问题。单级优化过程中,IDF 优化过程需要引入辅助设计变量及兼容性学科约束进行学科间的解耦,而本优化问题中的前向耦合变量难以解析,因此排除IDF优化过程。本优化问题虽然学科之间的数据传递关系较为复杂,但得益于工程估算方法的应用,不存在耗时较长的学科分析模型,弥补了MDF优化过程的最大不足。MDF 优化过程拥有最小的整体式构架,在实现复杂度上也存在优势。因此,本文选择MDF优化过程进行学科集成。 表1 MDO优化过程对比 本文优化问题的设计空间维数较高,寻优难度大,采用传统优化算法较难得到全局最优解,且其各个学科模型难以写出对变量的显式表达,求解灵敏度过程较为复杂。 差分进化算法(Differential Evolution,DE)的基本思想是在随机生成的种群中,将任意两个向量做差再与第三个向量求和,以此产生新的计算点。该算法不需计算灵敏度,且与其他进化算法相比,收敛速度较快, 正与本优化问题相适应。因此,本文选择DE为单目标优化问题求解算法,参数设置为种群规模85,初始步长0.5,缩放因子0.7,杂交概率0.85,平均终止步长0.01,求解流程如图5所示。 本文选择的多目标优化算法为法向边界求交法(Normal Boundary Intersection Method,NBI)。NBI的思想是先寻找每个单目标的最优解,将单目标最优解连线并做等距分层,分层数决定了Pareto点的个数。再通过权值不同的优化计算,找到该连线与Pareto前沿的所有交点。NBI所需迭代次数较多,且其结果生成的Pareto模型主要作用是为设计人员对多个目标的权衡进行一定的指导,故其中单目标优化算法采用收敛速度较快的非线性序列二次规划法(Nonlinear Programming Quadratic Line Search, NLPQL)。本文NBI层数设置为5。 图5 差分进化算法流程图 设计变量约束取值见表2。 表2 设计约束取值 单目标优化设计结果见表3,最优程序攻角曲线见图6。导弹飞行10 s左右,控制系统为使导弹快速从爬升段进入平飞段,进行高度控制,超调量导致攻角变化幅度较大。导弹飞行20 s后,程序攻角曲线渐趋平稳。 图6 最优程序攻角 表3 单目标优化问题的多学科设计优化结果 经过优化,小型战术导弹起飞质量减小了11.6%,验证了 MDO在导弹总体设计优化过程中具有适用性。翼弦的减小在降低升阻比的同时,也减小了质量,可看作是气动学科对质量学科的“让步”。而弹长的减小有利于减阻,弹翼展长的增大提高了升力,结合翼与尾翼轴向位置的移动,整体上导弹气动性能有所提高。一二段推力时间间隔tj的增加,降低了飞行速度的增长速度,有利于导弹的结构和气动防热设计,发动机总冲的降低,则有助于减小质量。将单目标优化问题的结果载入弹道模型进行计算,得到主要的弹道参数曲线如图7所示。 (a)Altitude-range curve (b)Speed-time curve (c)Trajectory angle-time curve (d)Overload-time curve 表4为多目标优化设计得到的结果。其中,在f1权重0.25、f2权重0.75时,NLPQL未收敛到满足所有约束的可行解。因此,故在构建Pareto模型时,将其排除。 表4 多目标优化结果 对点4以外的Pareto点进行拟合,得到的Pareto模型见图8。Pareto模型上的任意一点都代表一组两个目标不同权重的最优解,这种图形化的表达十分直观,设计人员可根据工程实际情况进行权衡。由图8可知,导弹射程与起飞质量正相关,一个目标增大必然使另一个目标随之增大。 在多目标优化得到的Pareto模型上,于x轴R=30 km处做一条平行于y轴的直线,得到对应的质量为98.40 kg,与单目标优化结果的误差为0.34 kg。误差主要来自两个方面:1)NBI中NLPQL不一定能收敛到全局最优解,这也导致拟合Pareto模型时, Pareto点与Pareto前沿存在一定的偏差;2)本次多目标优化中NBI层数设置为5,即只精确计算5个Pareto点。排除未收敛到可行解的Pareto点4, Pareto前沿上其余点的值由4个Pareto点拟合模型进行估算。NBI设置的层数越高,Pareto模型越精确,但计算时长也随之增加。实际应用中,应结合具体需求,选择合适的层数。 图8 Pareto模型 导弹总体设计具有多学科、多耦合、多变量、多约束等特点,与MDO理论针对的问题相符合。本文在MDO技术工程应用方面的工作如下: (1)建立了基于工程实际的小型战术导弹多学科优化设计模型,完成了各学科参数耦合优化,使导弹起飞质量降低了11.6%,并证明了多学科设计优化并非单学科最优的简单叠加; (2)通过对比单目标优化和多目标优化的结果,验证了得到的最优总体参数方案,证明了MDO技术可有效挖掘导弹总体设计潜力,具有较强的工程应用价值; (3)在OPTIMUS框架下,进行了小型战术导弹总体多学科优化模型的集成,搭建了小型战术导弹MDF优化过程工作流程,并验证了其可行性,实现了仿真分析流程自动化和智能化,为将MDO技术、OPTIMUS软件平台用于导弹总体设计提供了工程技术指导。2.2 多目标优化问题
3 多学科集成
3.1 设计结构矩阵
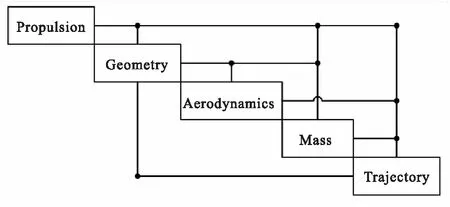
3.2 优化过程

4 多学科优化设计
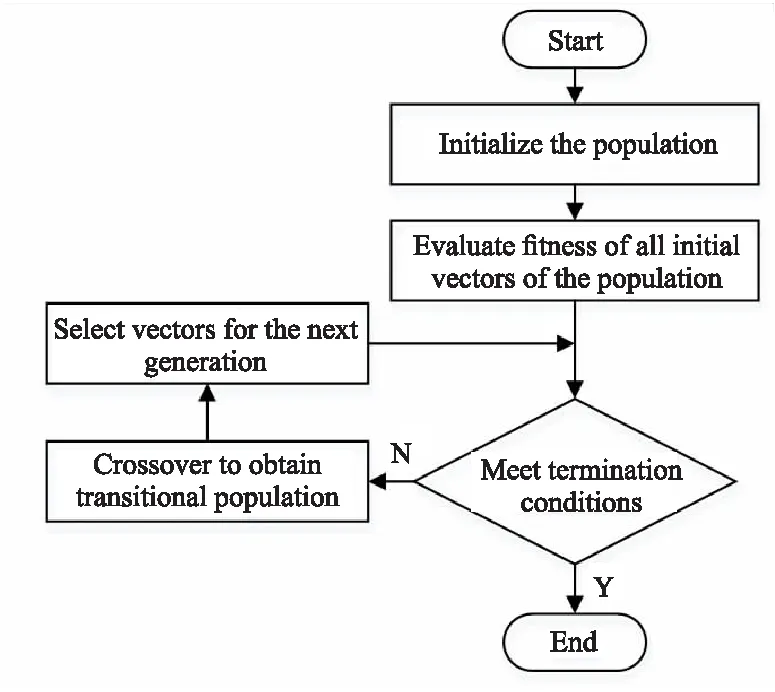
4.1 优化算法
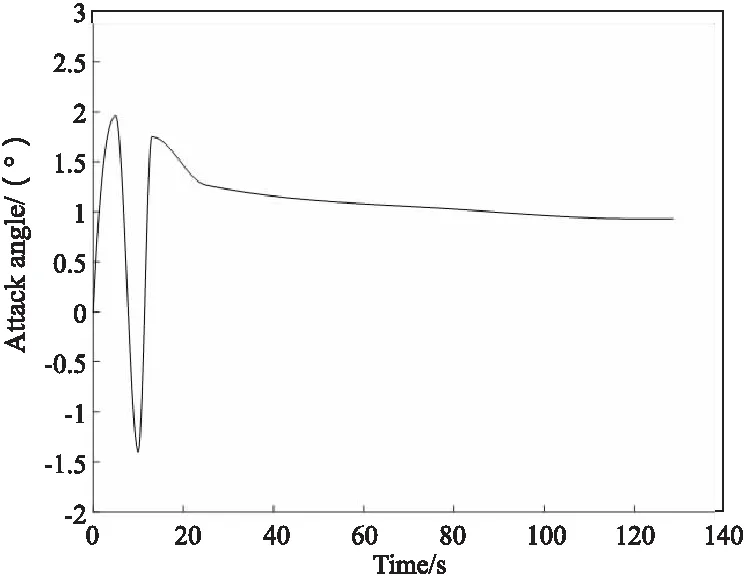
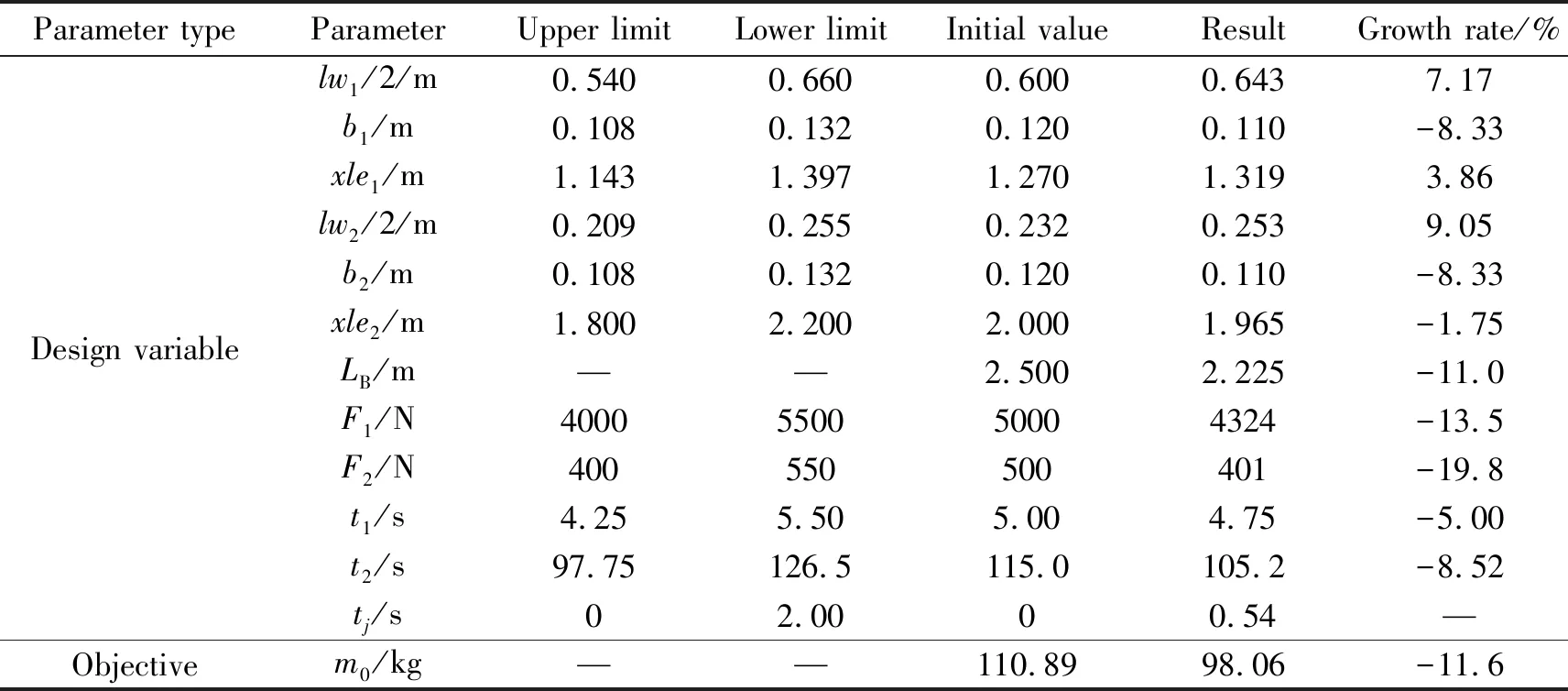
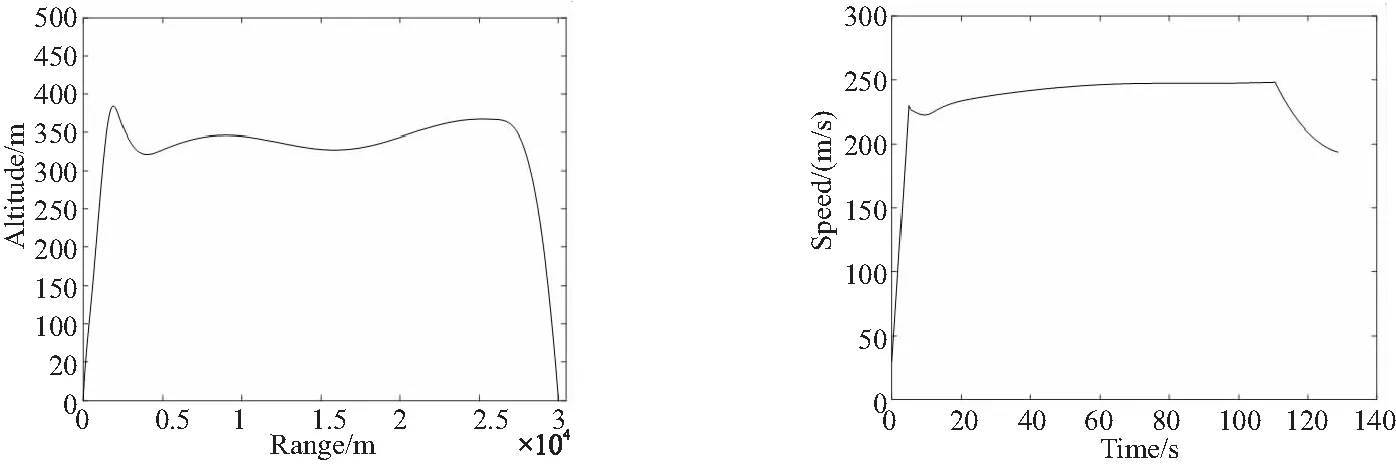
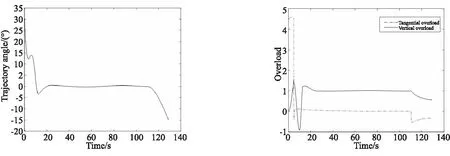
4.2 优化结果与分析


5 结论

