磁等离子体动力推力器加速机理研究与仿真①
赵博强,李 永,周 成,王 戈,王宝军,丛云天
(北京控制工程研究所,北京 100094)
0 引言
磁等离子体动力推力器(Magnetoplasmadynamic thruster,MPDT)利用大电流电离推进剂并注入能量,利用磁场和电场来加速等离子体而产生推力。MPDT属于电推进家族中的电磁推进,与静电推进相比,能够更容易做到大推力和大功率,并且效率更高。由国内外已发表的研究成果可知,MPDT的功率可达2 kW~11 MW,比冲范围2000~11 000 s,效率可达30%~70%。
目前,开展MPDT研究的机构有美国普林斯顿大学、NASA格伦研究中心、苏联能源设计局、火炬设计局等。这些单位开展了最大功率达数兆瓦的大功率MPD推力器研究[1]。但迄今为止,附加场磁等离子体推力器并没有达到令人满意的效率和比冲。研究认为,这是由于两个方面的原因:附加磁场的均匀程度、形状、强度都没达到推力器最佳工作的参数;等离子体在推力器中的加速机制和损耗机制并未完全掌握。其中,加速机理是制约推力器研究最重要的一方面。
磁等离子体动理推力器的推力理论目前还不成熟,相关的推力产生机理还不明确。针对推力器的试验结果有一些经验、半经验公式。FRADKIN,MYERS等[2-3]分别提出了基于经验的推力公式。MIKELLIDES等[4-5]基于磁流体力学方程推导了推力器的仿真程序,利用MACH2代码仿真了推力器。结果表明,利用磁流体方法可较好地仿真出推力器的工作状况。虽然目前根据经验和实验总结出的公式在一定情况下能够和实验结果相吻合,但并不能完全准确地描述推力器的工作情况。同时,经验公式不能反映推力器内部的加速机制,还需要进一步利用等离子体理论推导。文献[6]和文献[7]中,提出了一些利用磁流体和粒子模拟方法进行等离子体仿真的工作。文献[6]利用磁流体方程,对NASA的100 kW推力器进行了仿真,提出了一种基于密度的中心迎风求解格式,取得了不错的效果。文献[7]利用PIC/MCC方法,对自身场的推力器放电情况进行了研究。从上述文献可看出,目前MPD的仿真研究主要集中在推力器的几何尺寸与推力的关系,以及数值求解方法的研究上,而就磁场对等离子体的研究较少。现阶段推力器中磁场强度不是很高,仿真磁场对推力器的影响还不多。随着超导型磁等离子体推力器的出现,超导线圈极大地提高了附加磁场的强度[8]。研究附加磁场对推力器的影响就变得更加重要。
本文利用磁流体方程组,对磁等离子体动力推力器进行建模,提出了等离子体在磁场中电导率各向异性的建模方法,利用电导率模型,将磁场和等离子体耦合起来,从而对不同强度磁环境下的推力器进行仿真。
1 等离子体物理理论
分析等离子体主要有两种方法:磁流体方法和动理学方法[9]。由于磁等离子体推力器中等离子体浓度极大,满足磁流体方程连续性假设。磁流体方程组由连续性方程、动量方程、能量方程和麦克斯韦方程组和欧姆定律组成[10]。
连续性方程形式如下:
(1)
式中ρ为等离子体的密度,ρ=∑Nm;N和m分别为粒子的数密度和粒子的质量;V为等离子体的速度矢量。
对于MPDT而言,假设在工作中推进剂完全电离,在计算中需要考虑离子和电子两种成分,对每一种成分都需要一个方程来对应。
根据文献[11]中记载,在距离阴极出口几毫米地方的等离子体就已经完全电离,且在文献中观察到等离子体电离率也远大于Saha方程计算结果[11]。本文的仿真区域中等离子体电离度很高,仿真时为了简化计算,忽略了推进剂电离过程,认为等离子体已经完全电离。
动量方程形式如下:
(2)
式中I为单位张量;p为压力;τ为粘性应力张量。
能量方程形式如下:
(3)

在不考虑多种组分的情况下,上述方程组包含5个方程、6个物理量,分别是ρ、V、T和p。为使方程组闭合,还需要补充等离子体的状态方程。假设等离子体为理想气体,那么状态方程可表示为
p=p(ρ,T)=2NkT
对于单流体模型,假设离子温度和电子温度相同,双流体模型认为离子和电子处于不同的温度。
在等离子体中,电磁场由麦克斯韦方程组来计算:
式中ρq为电荷密度;E和B分别为电场矢量和磁场矢量;J为电流密度矢量,由欧姆定律给出。
J=σ(E+u×B)+ρqu
(4)
而电磁场对流体的作用力根据洛伦兹力公式计算:
F=ρqE+J×B
(5)
2 磁化等离子体的电导率
当一个离子和一个电子碰撞时,认为离子和电子之间只存在库仑力作用,假设离子使得电子运动方向偏转90°时,认为离子和电子发生了碰撞,离子和电子之间的库仑力为
(6)
式中r0为碰撞截面半径。
假设电子和离子之间是圆周运动,电子大约偏转1/4个圆周,整个过程运动时间为

碰撞截面为
(7)
电子和离子碰撞频率为
(8)
等离子体的电阻率为
(9)
以上方程都是基于大角碰撞产生的电阻率。实际上,由于库仑力是长程力,小角碰撞可能更加频繁。斯必泽证明,方程应乘上一个修正因子[10]。
(10)
(11)
对于麦克斯韦分布的电子,可用KT/m来代替v2,因此有
(12)
(13)
根据以往的试验和文献结果,lnΛ是一个和电子温度和浓度有关的物理量,在电子温度和浓度变化范围很大时,lnΛ变化范围比较小。因此,这里为了计算方便,假设lnΛ=10,对于MPDT中的等离子体,这个结果认为足够精确[10,12]。同时,MPDT中等离子体电子温度KT≈4 eV可计算得到,等离子体碰撞频率约为4.4×107s-1,等离子体的电阻率为5.284 4×10-5Ω·m。
上面公式为传统的无磁场条件下等离子体的电导率,在存在磁场的情况下[12],等离子体电导率为
(14)
其中
2.1 在弱磁场条件下ωce τ≤1
在弱磁场下垂直方向的电导率为
(15)
其中
霍尔电导率为
(16)
其中
平行磁场方向电导率为
σ‖=σ
(17)
(18)
2.2 在强磁场条件下ωce τ≥1
在强磁场下垂直方向的电导率为
(19)
其中
lnΛ3=lnΛ(ve3)
霍尔电导率为
(20)
式中c为光速。
平行磁场方向电导率为
σ‖=σ
(21)
3 AF-MPDT仿真方程组
磁等离子体推力器的仿真环境在低真空下进行,仿真时,电子和离子温度不相同。因此,利用双流体MHD方程组,对MPDT进行仿真[13-16]。
首先是电子和离子的质量守恒方程组:
(22)
(23)
式中ne和ni分别为电子和离子的密度;ue和ui分别为电子和离子的速度;m和M分别为电子和离子的质量。
MPDT工作条件是低真空情况下,且在推力器放电腔体内推进剂完全电离,假设在仿真区域内部为完全电离等离子体,只存在电子和离子。因此,连续性方程有两个。
电子和离子的质量守恒方程组为
(24)
(25)
式中Mei为电子离子动量交换项。
式中νei为电子离子碰撞频率。
电子和离子的能量守恒方程组为
(26)
(27)
其中

4 仿真
推力器模型如图 1所示。其中,左上角不规则区域为推力器放电腔和羽流区,深入放电腔的为阴极,放电腔左边壁为阳极。右侧矩形区域为磁线圈。剩余部分为仿真空间中磁场的自由空间。

图1 磁等离子体动力推力器模型
由于磁流体方程组是非线性的方程组,无法求解方程组的解析解,且在强磁场、高密度等离子体中,等离子体状态变化非常剧烈。因此,需要使用高分辨率的求解格式来对方程组进行数值求解[17-20]。
下面是对推力器不同工作情况下的仿真分析。工作条件为推进剂质量流量40 mg/s,工作电流320 A,中心磁场强度为1.54 T,仿真得到的工作电压236 V,离子速度约为46 800 m/s,计算得到推力约为1.87 N,功率约为75.5 kW。计算结果如图2所示。
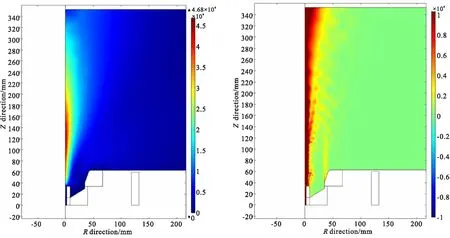
(a)Ion velocity under central magnetic field strength 1.54 T (b)Current density at 1.54 T for central magnetic field strength
推进剂质量流量40 mg/s,工作电流320 A,中心磁场强度为0.66 T,仿真得到的工作电压160 V,离子速度约为43 000 m/s,计算得到推力约为1.72 N,功率约为51.2 kW。计算结果如图3所示。
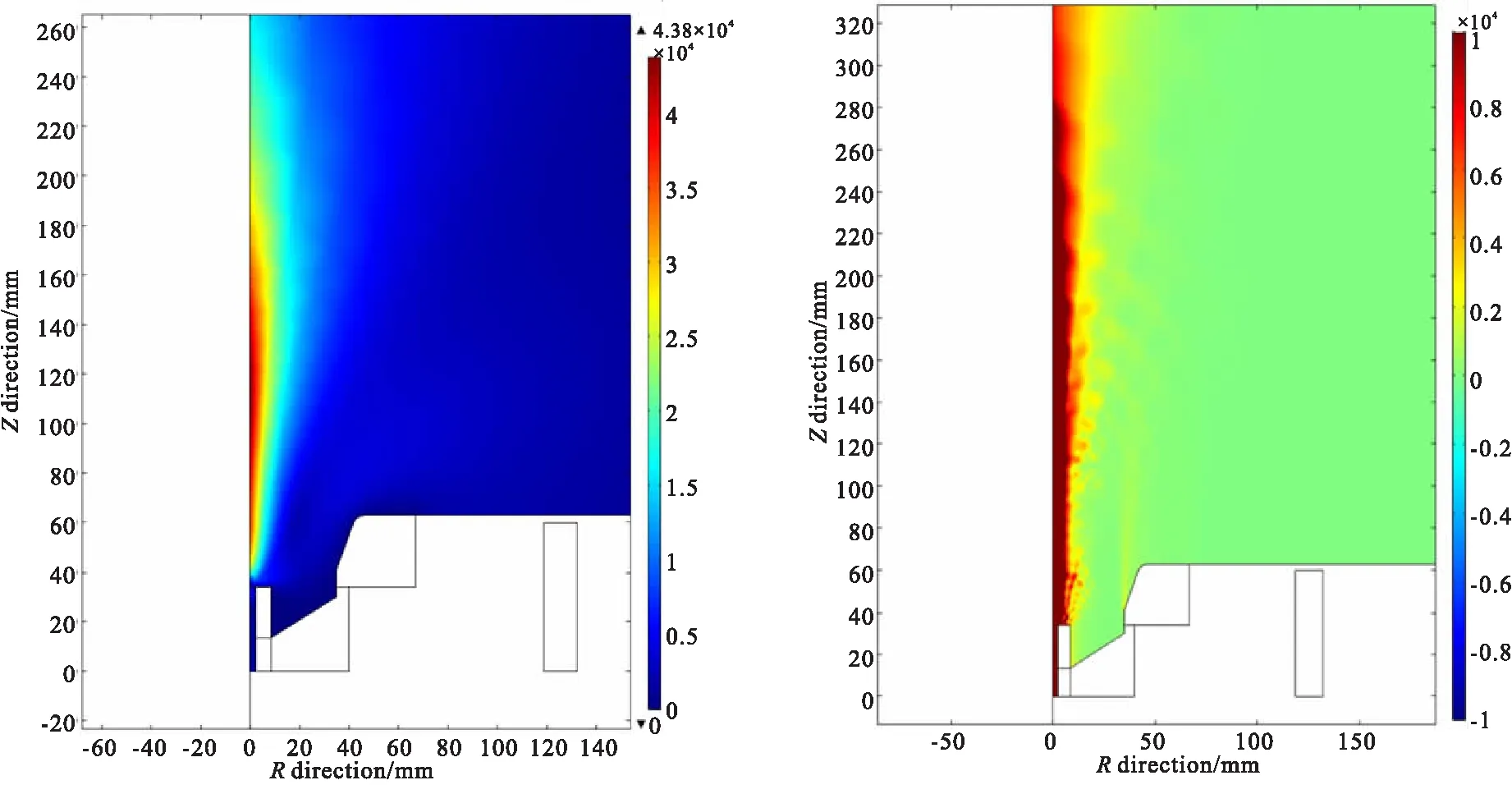
(a)Ion velocity under central magnetic field strength 0.66 T (b)Current density at 0.66 T for central magnetic field strength
推进剂质量流量40 mg/s,工作电流320 A,中心磁场强度为0.53 T,仿真得到的工作电压152 V,离子速度约为42 000 m/s,计算得到推力约为1.68 N,功率约为48.6 kW。计算结果如图4所示。

(a)Ion velocity under central magnetic field strength 0.53 T (b)Current density at 0.53 T for central magnetic field strength
推进剂质量流量40 mg/s,工作电流320 A,中心磁场强度为0.2 T,仿真得到的工作电压120 V,离子速度约为34 000 m/s,计算得到推力约为1.36 N,功率约为38 kW。计算结果如图5所示。

(a)Ion velocity under central magnetic field strength 0.2 T (b)Current density at 0.2 T for central magnetic field strength
仿真模拟了在恒定电流的情况下,通过调节推力器的附加磁场强度,得到不同工况下推力器参数。仿真了中心磁场1.54、0.53、0.66、0.2 T情况下推力器的工作情况。表1为仿真结果的汇总。

表1 仿真结果
根据理论分析[21-22],在磁场中,等离子体电导率出现各项异性,在推力器的轴向方向上电导率最大,电子和离子主要集中朝这个方向运动。
通过仿真可看出,在电流恒定的情况下,增强磁场,可使得电压增大,推力器工作的总功率增加,比冲和推力都增加。随着磁场强度的增加,推力器的效率会随着磁场的增加,先升高、再降低,说明磁场在0.6 T附近是当前推力器最好的磁场强度范围,适当的磁场能够提高能量注入的效率,低强度的磁场不能很好地约束等离子体,而过强的等离子体会导致等离子体电阻过大,能量损耗过大,也会导致效率降低。因此,磁场强度还需要和推力器尺寸相匹配,才能得到更好的效果。
根据理论和实验仿真还可推断出,在电压恒定的情况下提高磁场,可使推力器的电流密度降低,功率下降,等离子体获得的能量降低,但等离子体仍能保持较高的比冲,且电流降低可减少在热量在推力器总的产生,可减小阴极的烧蚀,并减轻电源的工作负担,对提高推力器的工作寿命和可靠性都有好处。
5 结论
本文通过磁流体力学方程组和等离子体理论,对磁等离子体推力器的磁流体模型进行推导,通过磁化等离子体电导率模型,将磁场和等离子体耦合起来,建立了在不同强度磁场环境下的磁流体模型,并对该模型进行了仿真。
通过仿真结果可看出,推力器比冲和电压随着磁场的增加而增加,这个结论和文献中是相符的。通过对推力器加速机理进行了分析,认为由于磁场导致等离子体电阻率增加,导致了更多的能量注入,且磁场对等离子体运动有约束作用,使得更多的等离子体沿着轴向喷出,从而提高了推力器的比冲和功率。在磁场增强之后,导致效率降低的问题还需要进一步的研究。
本文利用磁流体模型和电导率模型,对磁等离子体动力从理论上初步分析了磁场对推力器的影响,在工程上可为推力器的设计提供进一步的仿真依据,为以后的推力器设计和优化提供参考。

