基于存储缩减方案的WSN数据恢复算法

王 文 飞

(滁州职业技术学院信息工程学院， 安徽 滁州 239000)

0 前言

无线传感网(wireless sensor networks，WSN)是大数据体系下数据采集及重建的重要载体[1]。在传感网络初始化过程中，采用节点部署方式，使用无线组网技术实现数据采集、汇聚和传输，相应节点均具有便于制造的廉价特性[2]。由于数据汇聚过程完全依赖无线信道进行数据传输，sink节点接收数据时极易产生严重的数据丢失及混淆现象，使得网络工作效率下降。为了充分发掘数据价值，数据恢复方法成为当前无线传感网研究的热点之一[3]。实践中，多采取数学拟合方式进行传感数据恢复[4]。

Thomas等人提出了一种基于N级临近节点存留数据分析机制的WSN数据恢复算法[5]。该算法利用传感节点数据具有的相似特性，在确定数据丢失节点临近N级节点状态后，采用均衡分析方案估算丢失比率，从而实现丢失数据的还原及归真。该算法也存在一定的弊端，特别是在低密集环境下存在临近节点数据丢失现象，难以实现数据的完整还原。

Xu等人提出了一种基于插值还原方案的非参数WSN数据恢复算法[6]。该算法利用传感数据频谱在广域上的统一特性，依次替补传输节点丢失的信号频谱，采用非参数方式对数据进行多次恢复。该算法能使数据恢复效率得到显著提高，可有效规避因参数选取不当而难以高效恢复网络数据的问题，实际可操作性很强。不过，在应用中需要针对网络节点及传输中的数据进行长周期平稳窗口流动性评估，算法的收敛性能较差，难以实现大规模的应用推广。

Ghanbar等人基于多属性压缩感知机制，提出了一种差错率可控的WSN数据恢复算法[7]。该算法采用多属性建模方式提取恢复参数，对传输中的数据采用压缩感知方案进行特征捕捉，提高了数据恢复的准确性。此外，通过预测编码方案进一步降低数据恢复差错率。其不足之处是，需要进行泛建模操作，且存在建模参数过多的问题，无法适应稀疏网络节点分布情形，实践成本过高。

在本次研究中，尝试采用基于存储缩减方案的WSN数据恢复算法。首先，通过传感矩阵进行数据压缩感知，部分恢复传感节点丢失的数据，结合现有正常节点存量数据，采取缩减方式进行剩余数据恢复。然后，采取自感知方法设计骨干汇聚链路并确定传输节点，提高数据重构准确性并增强邻居节点对评估节点的失效监测效率，从而进一步提升数据恢复质量。

1 算法设计

本次算法主要由两部分内容构成：一是采用基于传感二次型优化传输的存储缩减方法进行数据压缩感知，最大限度地恢复传感数据；二是基于线性数据自感知方式恢复骨干链路，提高网络监测恢复效率。

1.1 基于传感二次型优化传输的存储缩减算法

对于典型无线传感网网络，采用随机部署模式[8]，将节点随机分布在区域内(见图1)。 设某一时刻网络中有n个节点，其数据矢量为D(n)，模型如下：

D(n)=Xn

(1)

式中：Xn表示当前时刻第n个节点对应的数据，n=1，2，…，i。

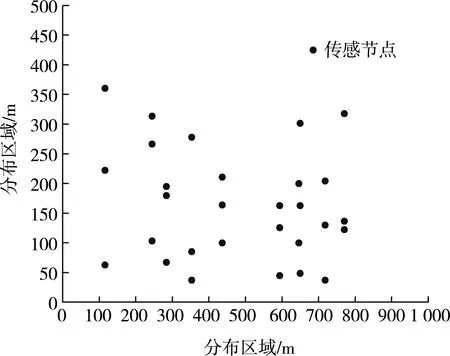
图1 网络部署图

任意节点在进行数据发送之前，根据当前节点数据随机抽样生成指纹矢量R(i)，i=1，2，…，n，模型如下：

R(i)=Ai

(2)

式中：Ai表示随机投影面积，可根据文献[9]所提供的方案获取。

传感节点同时进行数据收发的过程具有等价性，即同一时刻进出节点的数据流量相同。因此，按照以上模型在t时刻逐个对节点进行操作，即可获取各节点对应的数据矢量及指纹矢量。联立式(1)、(2)可得传感矩阵矢量Ht(n)，模型如下：

(3)

式中：t=mT，m=1，2，…，T表示数据传输周期。按传输周期对模型(3)进行计算并排序，获取传感矩阵H(n)：

(4)

由于传输过程中存在信道噪声，网络中sink节点获取的数据与初始数据之间存在一定的误差[10]，因此，sink节点最终获取的数据矢量T(n)可由以下模型获取：

T(n)=H(n)R(i)+G(n)

(5)

其中，G(n)表示各节点累计的信道噪声，可由如下模型获取：

G(n)=[G(1)，G(2)，…，G(i)，…，G(n)]K

(6)

式中：G(i)表示第i个节点的信道噪声；K表示转置操作。

为了降低传输误差，在此采用线性规划理论对模型(5)(6)进行降噪操作[11]：

T(n)=arg min‖T(i)‖i=1，2，…，n

(7)

‖T(n)-H(n)R(i)i=1，2…n‖≤ε

(8)

式中ε表示任意小的实数。

对模型(7)进行差分，可得：

Z(n)=T(n)-T(n-1)

(9)

联立模型(7)(8)，可得：

(10)

其中：

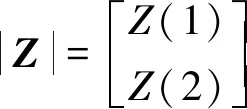
(11)

(12)

(13)

式中：Zi(j)表示第j周期内第i个节点按模型(9)获取的参数，模型(13)参数同模型(4)。到第n个周期时，通过模型(10)即可恢复相应的数据。

1.2 基于线性数据自感知机制的骨干链路恢复算法

无线传感节点均具有一定的拓扑移动能力[11]，且链路为双向传输，因此，可根据初始传输节点构建链路骨干链路树，并从中选取跳数最小的树枝作为传输链路。图2所示为基于线性数据自感知机制的骨干链路恢复过程。方案设计如下：

Step 1：针对任意初始节点i，构建初始链路树Tree(i，…，m，sink)。

Step 2 ：遍历初始链路树Tree(i，…，m，sink)，获取各节点的可达节点集合Ω。

Step 3 ：从Ω中获取Tree(i，…，m，sink)可达的最远节点，记为v。

Step 4 ：从Tree(i，…，m，sink)中搜寻与v距离最短的节点，记为u。

Step 5 ：将v与u进行连通操作，并转下一个初始节点i+1,继续从Step 1开始进行操作。

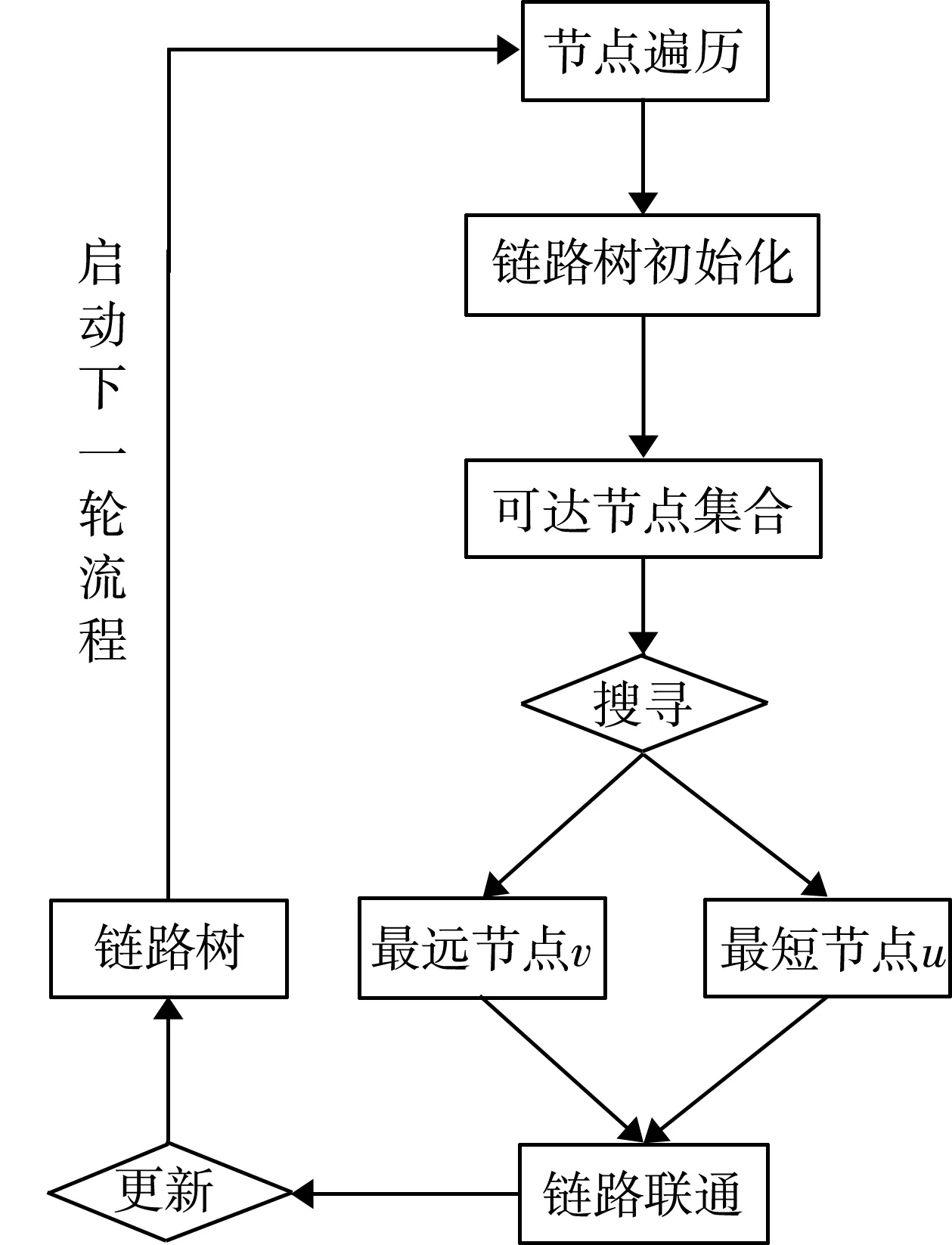
图2 基于线性数据自感知机制的骨干链路恢复过程

当链路恢复正常状态后，整体链路树可根据节点遍历方式进行实时更新。待链路树初始化完成，sink节点即可根据遍历链路树方式获取全部可达节点的集合。因此，将失效状态的节点予以剔除，可大幅减少因节点失效而导致的传输受阻现象。此外，筛选最短节点和最远节点时，可在网络中拓扑距离最远节点之间建立传输链路。该传输链路可作为备用链路用于数据恢复，且此项流程可根据网络拓扑状态进行实时更新，从而进一步提高对网络数据的恢复能力。

2 仿真实验

为了验证本次设计算法的性能，在Matlab仿真实验环境下，与当前无线传感网数据恢复领域常见的基于信任模型的无线传感器网络压缩感知数据恢复算法(trust based data prediction，aggregation and reconstruction using compressed sensing for clustered wireless sensor networks，TDBP-AR算法)[12]和基于单纯压缩感知机制的数据恢复算法(in-network data processing based on compressed sensing in WSN：a survey，DP-CS算法)[13]进行仿真对比。不失一般性，网络采取矩形布阵方式，节点均采用随机游走模型。此外，考虑到当前5G网络大规模推广的应用环境及其与WSN技术融合的特性，节点均采用128-PSK调制模式，传输信道采用莱斯信道。仿真参数如表1所示。

表1 仿真参数

2.1 数据恢复率

数据恢复率的仿真对比情况如图3所示。可以看出，本算法的数据恢复率较高且较为稳定。这是因为，本算法基于传感二次型优化传输的存储缩减方法，可通过指纹矢量逐个对当前节点及邻近节点进行数据匹配，特别是在匹配过程中引入线性规划理论对传输过程进行降噪操作，最大限度地降低了信道中莱斯噪声对数据恢复过程的不利影响。TDBP-AR算法采用邻近节点进行数据匹配，但进行数据恢复时采用的是均衡方式，未从网络节点整体数据及信道降噪的维度综合进行数据匹配，因此数据恢复率较低。DP-CS算法通过设计传输矩阵方式进行数据恢复，却采用一次成型模式进行有限传输感知，未能进一步采取差分模式优化恢复精度，因此数据恢复率也较低。

2.2 数据恢复时间

数据恢复时间对比情况如图4所示。可以看出，本算法的数据恢复时间始终最短，恢复最快，收敛性能最优。这是由于，本算法在基于传感二次型优化传输的存储缩减方法进行传输降噪操作的同时，针对无线传感网络骨干节点易瘫痪的问题设计了基于线性数据自感知机制的骨干链路恢复方案，能够从骨干链路树中迅速搜寻出传输性能优良的最佳路径。TDBP-AR算法仅考虑了数据层面的压缩感知，感知过程中采用的是简单均衡模型，未考虑传输链路的恢复，因此网络链路发生抖动的概率较高，使得数据恢复时间也大大延长。DP-CS算法存在传输感知受限问题，数据恢复过程比较单一，未综合数据-链路因素进行恢复，因此数据恢复时间较长。

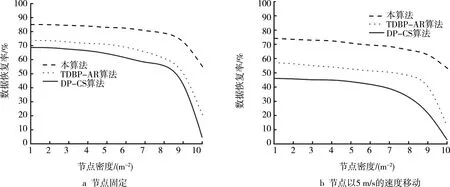
图3 数据恢复率

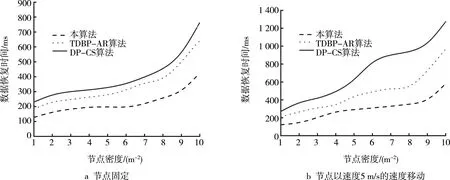
图4 数据恢复时间

3 结 语

为了解决当前无线传感网中数据恢复性能较差的问题，提出了一种基于存储缩减方案的WSN数据恢复算法。本算法主要由基于传感二次型优化传输的存储缩减和基于线性数据自感知机制的骨干链路恢复两部分构成，分别从数据层和链路层两方面对数据恢复性能进行了优化。其优势是，可显著提高数据恢复率，缩短数据恢复时间，具有较强的数据恢复效率和算法收敛能力，实际应用中部署价值较高。