敏感性稠油油藏水平井含水率预测模型研究

罗 宪 波

(中海石油(中国)有限公司天津分公司， 天津 300459)

稠油油藏的无水采油期较短，其主要采出阶段为中高含水期，在此过程中敏感性储层渗透率等物性参数随着注入速度、地层压力等外部条件的变化而不断发生变化。目前，水平井含水率动态变化预测仍是敏感性稠油油藏开发中的一个技术难点。现有的含水率预测研究，大多侧重于水平井的长度与含水率的关系、含水率与累计产量的关系、水平段不同部位含水率随时间的变化等，而较少关注敏感性储层变化对含水率变化规律的影响[1-4]。敏感性稠油油藏的水平井含水率变化比较复杂，其规律不易准确预测，数值模拟的历史拟合精度偏低。本次研究将建立敏感性油藏水平井含水预测数值模型，模拟含水率变化规律。针对敏感性油藏含水率规律预测难题，拟将不断降低的渗透率等价为不断增大的表皮因子，考虑速敏性、水敏性对近井地带和远井地带产生的影响，推导出油水两相二维渗流方程，构建含水率与表皮因子的关系式，从而模拟敏感性稠油油藏水平井的含水率变化规律。

1 水平井含水率预测模型的建立

1.1 模型的假设条件

假设在均质等厚地层中心钻遇一口水平井，其渗流模式如图1所示。该水平井采用裸眼方式完井，油层厚度为h， 水平段长度为L。该井的三维流场等效为远井地层的平面径向流(见图2)和近井地带的垂直径向流(见图3)。该井的储层均质且无限大，模型中考虑了储层水敏效应及储层污染的动态变化特征，忽略了毛细管力和重力的作用。

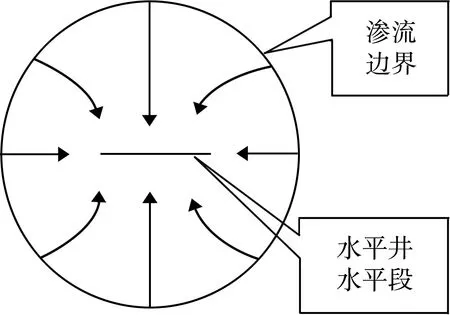
图1 水平井渗流示意图

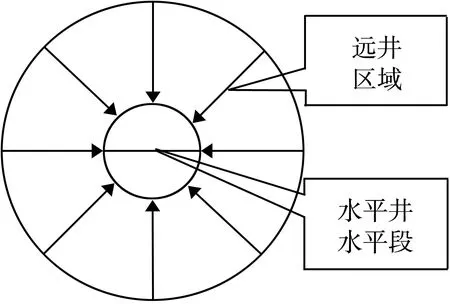
图2 水平井远井区域平面径向流示意图

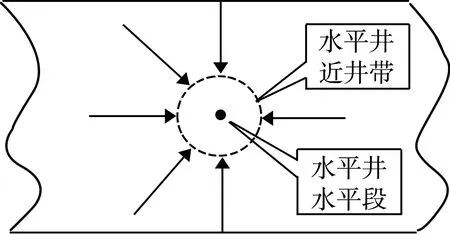
图3 水平井近井区域垂向径向流侧视图

1.2 模型的推导过程

水平井的产能计算公式主要有Borisov、Joshi、Giger和Renard-Dupuy公式等[5-9]。在辫状河储层，薄互层发育，主力储层多以正韵律为主，层内非均质性强，水平井的真实径向流不是呈圆形或椭圆形，而是呈不规则供给边界。Renard 和Dupuy公式充分考虑了不规则泄油半径的情况，在水平井产能计算中引入了等效泄油半径的概念。将该方法应用于多层砂岩储层水平井产能预测，产能公式如式(1)所示：

(1)

(2)

式中：q—— 日产油量，m3；

K—— 储层渗透率，μm2；

h—— 油层厚度， m；

pe—— 地层压力，MPa；

pwf—— 井底流压，MPa；

μ—— 原油黏度，mPa·s；

L—— 水平井长度，m；

Re—— 远井地带渗流阻力，(Pa·s)/(m3·m)；

Rw—— 近井地带渗流阻力，(Pa·s)/(m3·m)。

在远井地带，渗流主要表现为平面径向流，流线呈发散状流向生产井。此时，流体在流动过程中主要受到供给边界到水平井的渗流阻力的作用，此渗流阻力称为渗流外阻。根据式(1)，远井地带的渗流外阻计算如下：

(3)

在近井地带，渗流主要表现为垂向径向流。此时，流体在流动过程中主要受到地层上、下边界到水平段井筒的渗流阻力的作用，此渗流阻力称为渗流内阻。此渗流半径可以视为油井半径。根据式(1)，近井地带的渗流内阻计算如下：

(4)

根据等值渗流阻力法，水平井生产中的总渗流阻力为2个阻力的串联值，即总渗流阻力为远井地带与近井地带的渗流阻力之和。根据式(3)(4)，得到总渗流阻力计算公式：

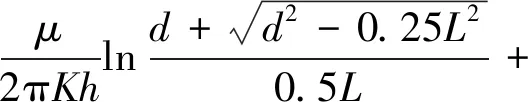
(5)

式中：R—— 总渗流阻力，(Pa·s)/(m3·m)。

在水平井的生产过程中，储层敏感位置不同，所产生的附加渗流阻力也有所不同。

对于速敏储层，由于近井地带生产压差大，出现微粒运移的概率也更大，所以附加渗流阻力主要产生在近井地带。假设该附加阻力所产生的附加表皮因子为Sw，其渗流阻力如式(6)所示：

(6)

(7)

(8)

对于敏感储层，总渗流阻力的计算如式(9)所示：

(9)

水平井见水之后，水平段内出现油水两相。在不考虑毛细管力和重力的作用时，油水两相二维渗流方程如式(10)所示[10-11]：

(10)

式中：p—— 压力，Pa；

Kw—— 水相渗透率，μm2；

Ko—— 油相渗透率，μm2；

μw—— 水相黏度，mPa·s；

μo—— 油相黏度，mPa·s；

vw—— 水相流速，m3/(m2·s)；

vo—— 油相流速，m3/(m2·s)；

x—— 渗流截面间的距离，m。

流经储层渗流横截面的水、油流量计算如式(11)(12)(13)所示：

(11)

(12)

Q=Qo+Qw

(13)

式中：Qw—— 水相流量，m3/s；

Qo—— 油相流量，m3/s；

A—— 渗流截面积，m2。

根据以上公式，推导出含水率的计算公式：

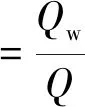
(14)

式中：fw—— 含水率，%。

由式(14)可知，含水率主要受油水黏度之比、油水相对渗透率之比的影响。对于常规稠油敏感储层，黏度μw、μo保持不变，而含水率能保持较小增幅，说明Kro/Krw的变化很小。这与相渗规律相差较远，说明储层相渗与原始状态存在差异。因此，引入变量表皮因子m，将不断变化的相渗特征加载至公式(14) ，修正后如式(15)：

(15)

式中：Kro—— 油相相对渗透率，μm2；

Krw—— 水相相对渗透率，μm2。

1.3 敏感性分析

根据式(15)绘制不同表皮因子m下的分流率曲线(见图4)。

图4反映了典型的敏感性储层开发现象：随着注水开发的持续，含水饱和度不断增加，含水率快速上升后再进入平稳阶段；随着m增大，平稳后的含水率降低。这也表明：储层渗透率降幅越大，污染就越严重；且表皮因子m越大，含水率平稳后的数值就越小。这是敏感性油藏水平井在低含水率下持续生产的主要原因。

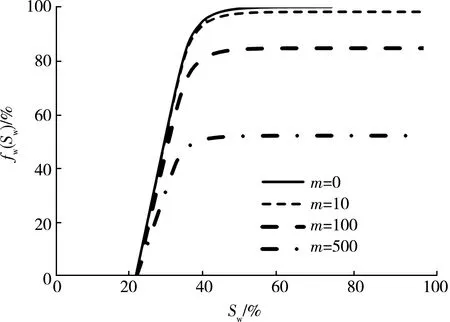
图4 不同表皮因子m下的分流率曲线

2 表皮系数与含水率的关系

在敏感性油藏开发过程中，渗透率等物性参数的不断变化使得水平井的含水率变化规律更加复杂，因而数模研究的历史拟合精度较低，最终影响到油田开发指标的预测结果。在此，通过修正历史拟合过程中的表皮因子S来提高拟合精度。根据前面公式，对已投产水平井历史生产过程中的表皮因子S进行修正，可得到不同表皮因子m下的含水率曲线，从而拟合出不同阶段的含水率曲线；同时，将不断降低的渗透率等价为不断增大的表皮因子S，以表征速敏性、水敏性对近井地带和远井地带的影响。

根据修正拟合所得含水率及其对应的附加表皮因子(S1)离散数据，绘制表皮因子-含水率(S1-fw)关系连续曲线(见图5)。

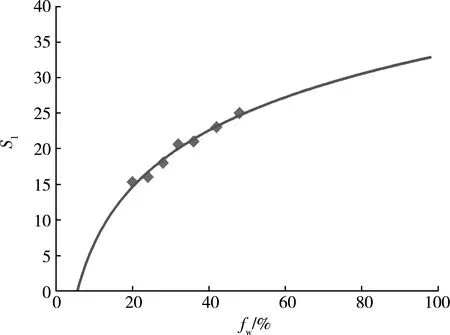
图5 水平井S1-fw关系曲线

从图5可以看出，不同的含水率对应不同的附加表皮因子S1。随着含水率的升高，表皮因子S1呈对数增大的趋势。通过非线性回归分析得到描述二者关系的方程式，如式(16)所示：

S1=11.483 1 ln(fw)-19.795 0

(16)

由式(16)可计算不同含水率所对应的附加表皮因子。对式(16)进行离散，构建S1-fw数据库，即可在数值模拟过程中得到不同含水率对应的总表皮因子，从而模拟敏感性油藏开发过程中储层物性变化所致等效表皮因子随含水率变化的动态规律。

3 模型实例验证

3.1 地质油藏概况

NNX油田是渤海湾盆地典型的薄互层状稠油油藏，极具埋藏浅、成藏晚、储量大、储层非均质性强等特征。主力含油层段为新近系的明化镇组和馆陶组，构造为复杂的封闭断块，沉积类型为典型的河流相沉积，储层发育较充分，平均孔隙度为28.5%，平均渗透率为950×10-3μm2，具有高孔隙度、高渗透率的特征，油藏类型为边水驱动的构造层状油藏。储层岩性主要为中 — 细砂岩及粉砂岩，成分以岩屑长石砂岩、长石岩屑砂岩为主。其中，石英的质量分数为45.0%～56.0%，长石的质量分数为35.9%～53%，岩屑的质量分数为38.2%～58.8%。填隙物主要为泥质杂基，其质量分数为11.3%～13.0%，平均为12.0%。其中的杂基主要为伊蒙混层，全岩平均含量为2.6%；另见伊利石、高岭石及少量绿泥石。油藏中部深度处的地层压力为12 MPa，油田的压力系数为1.0；油藏温度为56.5℃，地温梯度为3.0 ℃/hm，属于正常温度和压力系统。在评价井进行了多次PVT取样，研究区含油层段地层原油黏度范围为53～179 mPa·s，地面原油密度为0.952～0.966 g/cm3，原油饱和压力为8.53 ～ 9.94 MPa。

3.2 油田存在的问题

在NNX油田，储层的分选性差，孔喉类型以点状、片状为主，孔喉半径小(约11.4 μm)。储层中的细粒组分(直径小于0.015 6 mm)含量较高(约为12%)，其中黏土矿物的全岩含量高达8%，且以水敏矿物伊蒙混层(38.7%)、速敏矿物伊利石(21.4%)和高岭石(29.1%)为主。

由于储层孔喉半径小，伊蒙混层含量高，因此，当蒙脱石遇水膨胀时极易堵塞喉道，且易造成附着其上的细微颗粒脱落、运移，进一步加重喉道堵塞，导致储层发生水敏伤害。由于高岭石、伊利石及其他细微颗粒组分的含量较高，因此，在流体的快速冲刷下这些颗粒不断发生脱落，并在细小喉道处堵塞、堆积，降低物性，进而造成速敏伤害。实验结果显示，NNX油田储层表现出中等偏强的水敏特征以及中等 — 强的速敏特征。

NNX油田属于敏感性油藏，随着开发的持续进行，油井含水率也在逐步上升。采用初期固定表皮因子S0，对该油田近年来的水平井含水率历史数据进行了拟合，结果如图6所示。可以看出，随着油井含水率不断上升，含水率计算结果与实际含水率的差异逐渐加大。这说明历史拟合程度较差，数值模拟预测结果难以准确反映实际情况。

图6 采用固定表皮因子时的水平井含水率历史拟合曲线

3.3 修正模型的应用结果

经过本次模型修正，构建表皮因子与含水率方程，将由于储层敏感而产生的附加表皮因子S1加载至模型中，含水率计算结果与水平井的实际含水率吻合度非常高(见图7)。拟合结果准确地表征了敏感性储层裸眼筛管井含水率的变化规律，由此验证了该方法的可行性。

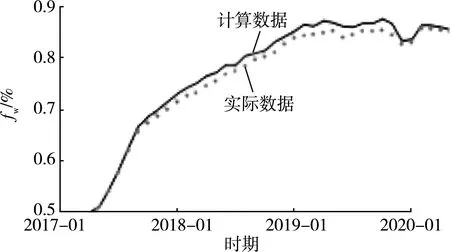
图7 修正模型的水平井含水率历史拟合曲线

4 结 语

在本次研究中，将不断降低的渗透率等价为不断增大的表皮因子，推导出考虑了水敏性和速敏性的油水两相二维渗流方程，探讨敏感性稠油油藏中水平井含水规律的模拟方法。通过对敏感储层实际生产数据的拟合，验证了该方法的可行性。在不同敏感储层水平井的生产过程中，产生附加渗流阻力的区域也有差异。在速敏储层，附加渗流阻力主要发生在近井地带；在水敏储层，附加渗流阻力在近井地带和远井带均有可能发生。实例应用结果表明，应用新模型可大幅提高历史拟合的精度，且计算简便。