IGCC电厂合成气中的单颗粒在驻波声场作用下的数值模拟

张斯宏 刘贝贝 许红 / 上海市计量测试技术研究

0 引言

整体煤气化联合循环（Integrated Gasification Combined Cycle，IGCC）发电技术是世界公认的清洁、高效煤基发电技术，也是实现我国节能减排目标技术路线的重要技术。目前，从高温合成气中有效去除燃煤飞灰颗粒、脱硫剂及其他杂质，确保高温合成气的洁净以及燃气轮机正常的使用寿命，是IGCC技术走向商业化面对的最大难题之一[1-2]。西班牙及荷兰IGCC项目在燃机燃烧器喷嘴、合成气管路阀门、燃机叶片等处均发现有管路锈蚀产生的杂质，对燃机的运行产生了重大影响。合成气中的大固体颗粒进入燃气轮机透平，直接损伤透平叶片，小颗粒也会对燃气轮机的通流部分造成磨损，并划伤沿途阀门设备的密封面，造成设备密封性下降。而燃气轮机是IGCC发电技术中的关键设备，因此，在合成气进入燃机燃烧室之前，必须进行过滤，去除颗粒[3]。另外，在IGCC项目中对脱硫后的合成气需进行加湿饱和，从而降低燃气轮机燃烧室绝热燃烧温度，控制NOX的排放量[4-7]。而加湿后的气体有助于颗粒间相互团聚，从而达到有效去除的目的[8-11]。同时，声凝并是一种极具发展潜力的颗粒脱除预处理技术。其原理是利用外加声场促使细微颗粒凝并长大为较大颗粒后，再利用常规除尘器加以脱除[12-13]。因此，可以在合成气经蒸气饱和器加湿饱和后进入燃机之前添加声场。本文从声波波动方程出发，建立水平驻波声场中的颗粒动力学模型，利用数值模拟方法研究在IGCC电厂合成气中，颗粒在驻波声场作用下的动力学特性，以充分掌握颗粒在声场中的运动机理及行为规律，进一步为高温除尘提供理论依据。

1 数学模型及数值计算方法

颗粒运动是气固两相流中所包含的基本现象，是研究颗粒之间相对运动、碰撞接触，以至凝并的基础。为着重探讨单颗粒在IGCC电厂合成气中的动力学特性，提出以下简化假设：

1）忽略颗粒在受力和运动过程中可能发生的形变，认为颗粒为刚性球体；

2）忽略声尾流、声辐射压力等对颗粒运动的影响；

3）忽略颗粒之间的相互作用力，认为颗粒之间互不相关；

4）忽略颗粒的旋转。

1.1 驻波声场波动方程

沿x轴方向波动的水平驻波声场可用介质振动速度方程来描述[14]

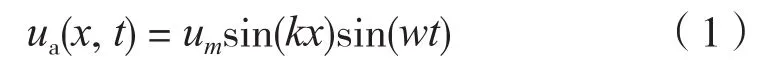
式中：ua——声场引起的介质振动速度，m·s-1；

um——速度振幅，m·s-1；

k——声场波数，k=ω/c，m-1；

c——声速，m·s-1；

x——位置坐标，m；

t——时间，s

通常采用声压级和频率来描述声场。声压级的表达式为

式中：L——声压级，dB；

ρg——合成气的密度，kg·m-3；

pr——参考声压，=2×10-5Pa

声速c的表达式为[15]

式中：R——通用摩尔气体常数，= 8.314 J/mol·K；

M——合成气的摩尔质量，kg/mol；

T——气体的温度，K；

γ——合成气的比热比，表达式为

式中：cp——合成气的定压比热；

cv——合成气的定容比热

1.2 合成气物性参数的确定

表1为某IGCC电厂合成气各成分的实际配比[16]。

表2 各气体的定压比热表达式[17]

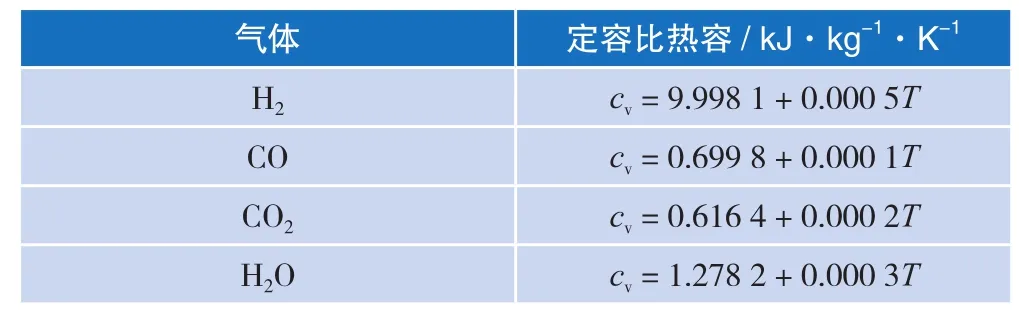
表3 各气体的定容比热表达式[18]

1.2.1 合成气摩尔质量

合成气摩尔质量M表达式为

式中：p——合成气的压力，Pa；

Mvapor——水蒸气摩尔质量，

Mvapor= 0.018 02 kg/mol；

Mdry——干合成气摩尔质量，kg/mol，其表达式为

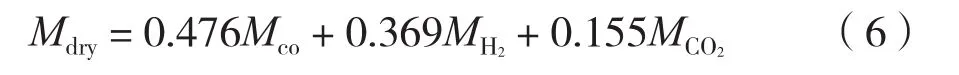
式中：MCO——一氧化碳摩尔质量，

MCO= 0.028 010 4 kg/mol；

MH2——氢气摩尔质量，

MH2= 0.002 015 88 kg/mol；

MCO2——二氧化碳摩尔质量，

MCO2= 0.044 01 kg/mol；

pvapor——水蒸气饱和压力，Pa，表达式为[19]

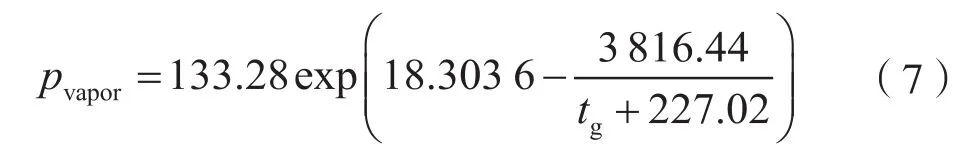
式中：tg——气体的摄氏温度,℃

1.2.2 合成气密度

合成气密度ρg的表达式为

1.2.3 合成气动力黏度

合成气动力黏度μg的表达式为[20]

式中：μj——合成气组分j的动力黏度，Pa·s；

Xj——合成气组分j的摩尔分数；

Mj——合成气组j的摩尔质量，kg/mol

μj的表达式可用Sutherland公式[21]：

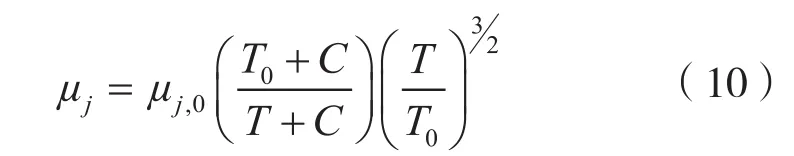
式中：μj,0——0 ℃时组分j的动力黏度；

T0= 273.15 K；

C——常数，K，决定于组分种类

具体取值见表4。

表4 各气体μj,0和C值

1.2.4 气体分子平均自由程

气体分子平均自由程λg的表达式为[22]

1.3 颗粒动力学模型

水平驻波作用于气体和颗粒组成的气固两相体系时，在假设条件下，水平方向上颗粒将受到斯托克斯力、压力梯度力、倍瑟特力和虚拟质量力。因此，颗粒在水平方向的运动方程可写为

式中：mp——颗粒质量，mp= πdp3ρp/6；

ρp——颗粒密度；

dp——颗粒直径；

upx——声波引起的颗粒运动速度；

Fst——斯托克斯力；

Fb——倍瑟特力；

Fp——压力梯度力；

Fvm——虚拟质量力

斯托克斯力表达式为

式中：Cc——肯宁汉修正系数，表达式为

式中：Kn为克努森数，Kn= 2λg/dp：

倍瑟特力表达式为

压力梯度力表达式为

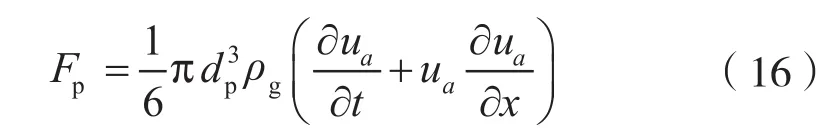
虚拟质量力表达式为

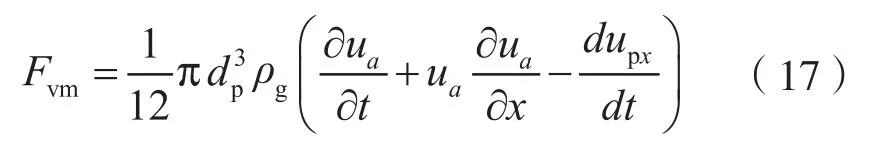
1.4 颗粒动力学模型

本文采用文献[23]提供的解析式求解倍瑟特力

式中：h——时间步长；

f(τ) =ua-upx——流体介质与颗粒的速度差；

τk=t-kh，k= 0，1，2，…，N

2 数值模拟结果

本文的数值模拟条件见表5。

表5 数值模拟条件

取颗粒的初始位置为3λ/8，模拟结果如1图所示。

2.1 颗粒所受作用力

2.1.1 颗粒受到的斯托克斯力的大小

由式（13）可知，斯托克斯力的大小和颗粒的大小以及颗粒与流体介质速度差有关。图1给出了颗粒受到的斯托克斯力的大小分布。从图1可看出，斯托克斯力的数量级为10-12N。

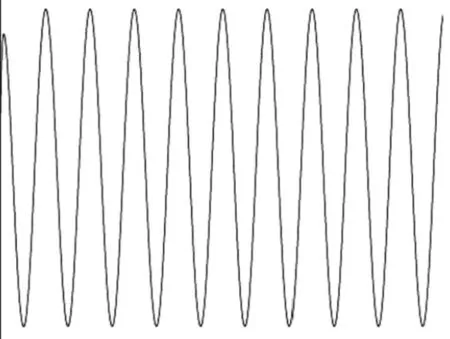
图1 声场中斯托克斯力随时间的变化

2.1.2 颗粒受到的倍瑟特力的大小

由式（15）可知，倍瑟特力的大小和颗粒的大小、流体密度以及颗粒与流体之间的相对加速度有关。图2给出了颗粒受到的倍瑟特力的大小分布。从图2可看出，倍瑟特力的数量级为10-13N，小于斯托克斯力。

图2 声场中倍瑟特力随时间的变化

2.1.3 颗粒受到的压力梯度力的大小

由式（16）可知，压力梯度力的大小和颗粒的大小以及流场压力梯度有关。图3 给出了颗粒受到的压力梯度力的大小分布。从图3可看出，压力梯度力的数量级为10-14N，小于倍瑟特力。

图3 声场中压力梯度力随时间的变化

2.1.4 颗粒受到的虚拟质量力的大小

由式（17）可知，虚拟质量力的大小和颗粒的大小、流体密度以及颗粒与流体之间的相对加速度有关。图4给出了颗粒受到的虚拟质量力的大小分布。从图4可看出，虚拟质量力的数量级为 10-15N，在所有作用力中为最小。

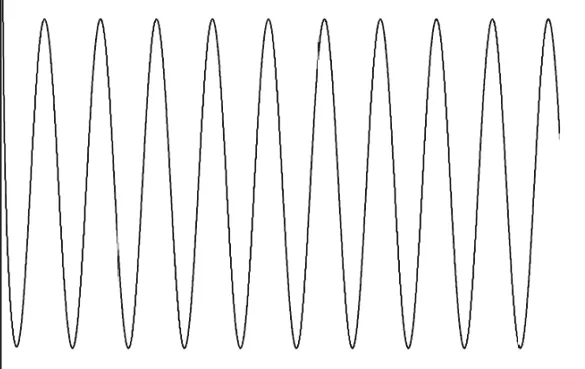
图4 声场中虚拟质量力随时间的变化

因此，斯托克斯力在颗粒运动中起主导作用。且所有作用力均呈现周期性变化。沿声波传播方向正、负受力交替产生。

2.2 颗粒的运动

颗粒的受力将直接影响到其运动规律。以下将分别介绍颗粒的位移和速度。

2.2.1 颗粒的位移

图5给出了颗粒位移随时间的变化。从图5可看出，颗粒在驻波声场中做周期性往复振动。

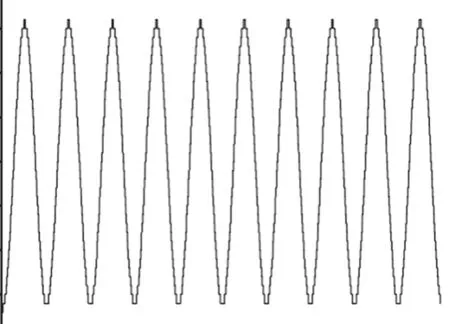
图5 声场中位移随时间的变化

2.2.2 颗粒的速度

图6给出了颗粒速度随时间的变化。从图6可看出，颗粒在驻波声场中做周期性变速运动，正、负速度幅值均为0.1 m/s。

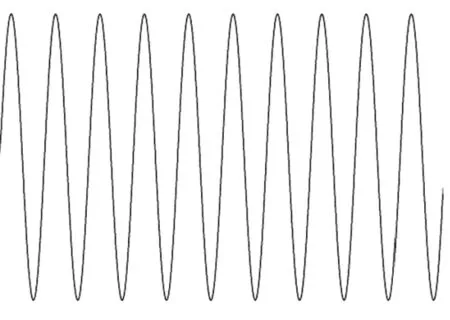
图6 声场中速度随时间的变化

3 结语

根据颗粒动力学理论，建立在IGCC电厂合成气中水平驻波声场作用下球形颗粒的动力学模型，得到如下结论：

1）颗粒在声场中受到大小和方向都在不断变化的作用力，沿声波传播方向正、负受力交替产生。从而，颗粒做周期性变速运动。在本文所列计算条件下，最大运动速度可达0.1 m/s。

2）斯托克斯力对颗粒在声波传播方向的运动起主导作用；考虑倍瑟特力的作用，可使数值计算结果更为准确；压力梯度力和虚拟质量力对颗粒运动的影响小于倍瑟特力。