基于机器视觉尺寸测量装置的误差不确定度评定

唐松 张一帆 沈意吉 / 上海市计量测试技术研究院

0 引言

随着生产科技的迅猛发展，人们对零部件尺寸测量方法和工具的测量准确度、测量效率及其自动化程度提出了越来越高的要求[1]。基于机器视觉的几何尺寸测量技术作为一种非接触的无损测量方法，具有自动化水平高、柔性好以及智能程度高等优点，现已成为几何尺寸测量领域的研究热点。

同时，在类似万向节外圈外卡槽等具有特殊结构的机械构件边沿高度测量领域，传统测量方式很难在满足测量准确度的情况下实现在线自动测量。通过综合分析相关机械构件边沿处待测几何量的特点和现有的测量技术，本文设计了基于机器视觉的测量技术的机械构件边沿尺寸自动测量装置，并针对测量结果进行了不确定度的评价。

1 测量原理及误差来源

1.1 测量原理

如图1所示，基于机器视觉的机械构件边沿高度测量装置（以下简称测量装置）由CCD相机、双远心光学镜头、平行背光光源、精密定位平台组成。将被测物体置于平行背光光源前,光线均匀地由被测物体背后射出，经过具有稳定放大倍数和大景深、微畸变的双远心光学镜头，可在CCD相机的感光元件上形成清晰的被测物体轮廓信息，最后利用图像处理技术来实现对被测物体轮廓信息的亚像素的定位和拟合，完成亚像素级准确度的测量。

图1 高度测量装置

1.2 测量误差来源

测量装置的测量误差来源主要有两个方面，一方面由测量过程引入的系统测量误差；另一方面由参考标准二等量块偏差引入的测量误差。其中，由测量过程引入的系统测量误差包含了图像获取系统和定位成像系统引入的测量误差。

2 测量装置的不确定度分析

2.1 标准不确定度

2.1.1 测量过程引入的标准不确定度分量

测量过程引入的标准不确定度分量也就是测量装置的系统误差所引入的标准不确定度分量[2]。本文主要对测量过程中由图像获取系统和定位成像系统所引入的标准不确定度分量进行了分析。

1）图像获取系统引入的标准不确定度分量

测量装置的图像获取环节是后续图像处理的基础和保证[3]。如图2所示，获取图像的质量直接关系到后续图像处理的难度以及处理结果的准确度。图像获取系统的不确定度分量主要由CCD相机噪声引入的不确定度分量和双远心光学镜头畸变引入的标准不确定度分量组成。

图2 视觉测量流程

（1）CCD相机

由于实际被测对象大小不超过20 mm×15 mm，同时根据实践经验，目标视场（FOV）的感光区投影面积一般不大于总面积的百分之八十，所以计算时目标FOV面积取25 mm×19 mm。其次，根据被测对象测量准确度一般要求为最大允许公差范围的1/10，因此，理论上所选摄像机分辨力需满足测量准确度为0.01 mm的要求，故选择了分辨力为2 448×2 050，靶面为2/3''的GC2450工业相机。由此可知，单位像素的实际尺寸dp为

式中：F（VorH）—— 视场面积

根据Healy和Kondepudy所建立的CCD噪声理论[4]，在信噪比高于15 dB时，测量不确定度低于1/3dp[5]，同时本文采用亚像素图像提取技术，噪声误差在一个像素内服从均匀分布，则相机噪声引入的标准不确定度分量u1.1.1为

（2）双远心光学镜头

本文选择了Vison Datum的CLW-5MP-0.3X-110超高清双远心光学镜头，根据其技术标准参数可知，其光学畸变小于0.01%，且服从正态分布，则镜头畸变引入的标准不确定度分量u1.1.2为

由于上述CCD相机和双远心光学镜头所引入的标准不确定度分量u1.1.1、u1.1.2彼此独立不相关，可得图像获取系统引入的标准不确定度分量u1.1

2）定位成像系统引入的标准不确定度分量

成像系统的标准不确定度分量主要来源于两个方面，分别因成像系统轴向的物面[如图3中M（X，Y，0）面] 垂直偏移引入的测量误差的标准不确定度分量和平行偏移（如图3中Zc方向）引入的测量误差的标准不确定度分量。

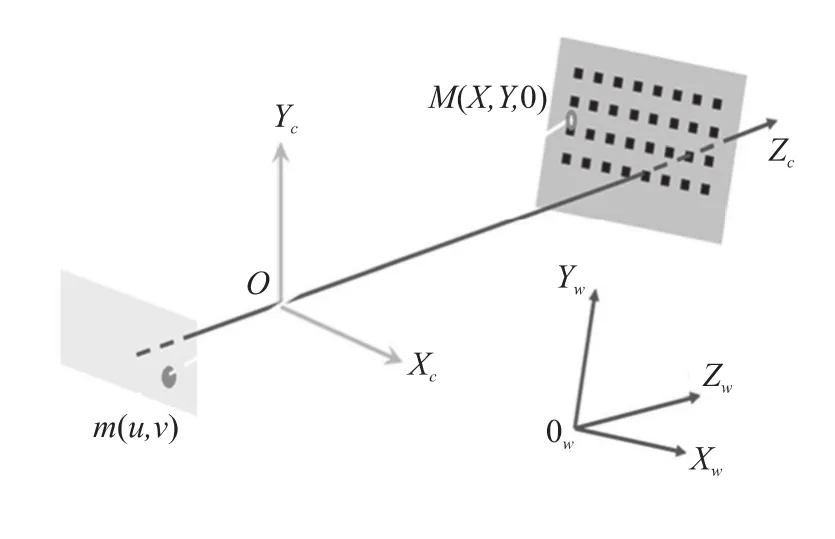
图3 成像系统坐标系模型

（1）物面定位误差引入的标准不确定度分量

基于图像的测量通常都是利用小孔成像原理实现的，即利用数字图像相关方法获得的实际位移H和图像位移h之间的线性关系来实现测量。但是由于受许多不利因素的影响，实际测量过程中不存在理想的线性关系。正是由于这种被测平面（物面）与相机传感器平面（像面）间的不完全平行，导致必然存在测量偏差[6]。

由于被测零件垂直成像系统轴向的平面存在定位偏差，导致实际物面与理论物面存在一定的角度偏移，如图4所示，O是相机光心，OA是相机光轴，EF'所在的面为相机成像面，AC'所在的面为与EF'所在的相机成像面平行的物面，AC所在的面表示为偏离AC'所在的物面θ角度的物面。理论情况下，C'点对应于像面的F'点，当目标像面从AC'偏移到AC，偏移角度为θ后，C'点移动到C点，其像面上的像点也相应地从F'点移动到F点，因此，由角度偏移引起的误差为F'F。

图4 物面偏移剖面

假设物面上出现了一个由A向C'方向的微小移动，位移量为H'，则在像面上发生相应地由E向F'方向的位移量h'。但由于角度偏转θ的影响，对应物面上产生了由A向C方向的位移，位移量为H，且H'=H。像面上的相应位移为从E向F方向，位移量为h。则由于角度偏移引起dOE=f的误差为d=Δh=h'-h。进一步假定dOA=z，dOE=f，CB与OA平行，由于ΔOAD与ΔCBD相似，因而

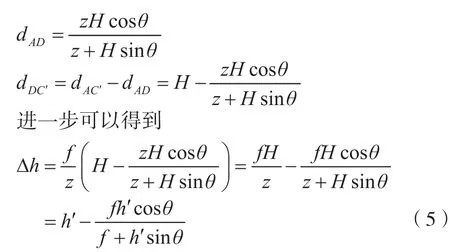
式（5）即由于摄像机光轴和物面不完全垂直而产生的误差表达式。一般情况下相机焦距f远大于h'，且由于θ通常较小，所以式（5）可以简化为

由小孔成像原理可知：

式中：ΔH——由角度偏移带来的物面偏移量

由式（7）可知，当位移量与偏移角度都较小时，实际误差和位移δx量及偏移角度的余弦成线性关系。同时由于测量装置的物面定位误差为δx= 0.591 6 mm和双远心光学镜头的成像物距L= 110 mm，可得偏移角度θ为

由式（8）的θ值可得物面定位误差引入的标准不确定度分量u1.2.1为

（2）轴向定位误差引入的标准不确定度分量

轴向的定位误差主要由于双远心光学镜头的工作距离发生了变化，导致图像的成像倍数变化，从而引起图像非正常的压缩或拉伸误差[7]。理想的物方远心透镜通过在物镜焦平面嵌入孔径光阑，使光线从无穷远处射入。然而，实际过程中，孔径光阑不可能完全位于焦点平面上，所以通常物方远心透镜将入瞳位置调试到较远处，让光学系统近似为远心光路。由于存在上述情况，物方主光线与光轴之间实际会有一个很小的夹角β，如图5所示，夹角大小即为远心度。

图5 双远心光学镜头成像误差

由于远心度的存在，当物体偏离最佳工作距离时导致成像结果出现误差，并且这种误差会与远心度的大小成正相关关系。实际物方远心透镜的加工误差可以分为孔径光阑在焦面点前和焦面点后两种情况，相应地使实际成像偏大或偏小，这里主要以孔径光阑在焦面点后的情况为例进行说明。根据前述远心透镜的远心度β≤0.21°和测量装置的轴面定位误差为δy= 0.459 8 mm，由图5的几何关系可得轴向定位误差引入的标准不确定度分量u1.2.2为

对比式（9）和式（10）可知，相较轴向定位误差引入的标准不确定度分量，物面定位误差引入的标准不确定度分量可忽略不计。即定位成像系统引入的标准不确定度分量u1.2为

所以在实际测量时要尽可能保证被测零件的轴向定位准确度，以保证最终测量装置的测量准确度。

最后,综合上述各不确定度分量可得测量过程引入的标准不确定度分量u1为

2.1.2 量块偏差引入的标准不确定度分量

本文设计的测量装置选择了具有稳定状态标称值为10 mm的二等量块作为参考标准。根据10 mm二等量块的检定证书可知其长度偏差在0.5 μm以内，故按正态分布计算，由量块偏差引入的标准不确定度分量u2为

对比标准不确定度分量u1.1、u1.2，该项标准不确定度分量可忽略不计。

2.2 合成标准不确定度

主要标准不确定度分量汇总如表2所示。

表1 标准不确定度分量汇总

由于上述各分项所引入的标准不确定度彼此独立不相关，且忽略由量块偏差引入的标准不确定度分量，可得测量的合成标准不确定度为

2.3 扩展不确定度

由于整个测量过程服从正态分布，故取包含因子k= 2，则扩展不确定为

3 结语

本文所设计的基于机器视觉的尺寸测量装置，针对类似万向节外圈外卡槽等具有特殊结构的被测对象的边沿高度，可以在满足最大允许误差在0.1 mm的测量要求前提下实现在线自动测量，通过对上述测量误差的不确定度分析验证了该装置的可行性，也对工业特殊结构零部件的尺寸准确测量提供了参考。