基于连续介质损伤力学的坑蚀钢筋高周疲劳寿命与损伤分析

张 昉, 金伟良, 张 军, 毛江鸿, 樊玮洁

(1.浙江大学 结构工程研究所, 浙江 杭州 310058; 2.浙大宁波理工学院 土木建筑工程学院, 浙江 宁波 315100)

大量沿海钢筋混凝土桥梁在服役过程中同时遭受氯盐侵蚀和车辆反复荷载作用.氯盐侵蚀下钢筋锈蚀形态多为坑蚀[1],造成钢筋截面积减小和应力集中,在反复荷载作用下极易发生疲劳断裂[2],严重降低钢筋混凝土结构的服役寿命[3].

S-N曲线法是预测锈蚀钢筋疲劳寿命的重要方法.已有研究[4-5]表明,在双对数坐标下,锈蚀钢筋的疲劳寿命和应力幅值仍然为线性关系,并建立了考虑锈蚀率的锈蚀钢筋的S-N曲线方程.该方法需要大量的疲劳试验,只关注疲劳寿命而忽略了疲劳损伤的非线性发展过程,也无法探明钢筋锈蚀对其疲劳性能的影响机理.此外,断裂力学(FM)可以很好地描述疲劳裂纹扩展行为,并预测疲劳寿命,如卫军等[6]研究了半椭圆形蚀坑钢筋裂纹扩展规律;Sun等[7]建立了最大蚀坑深度和锈蚀率的关系式,定义等效初始裂纹尺寸以提高构件疲劳寿命的预测精度等.一方面,FM法适用于单个裂纹占主导的情况,往往还需要对不规则蚀坑缺陷做简化等效处理[8],难以考虑钢筋多蚀坑之间的互相影响.另一方面,FM法主要研究疲劳裂纹扩展计算方法,无法给出疲劳损伤累积和局部应力场的演化.

基于热力学理论,连续介质损伤力学(CDM)通过定义损伤变量来研究反复荷载作用下材料力学性能退化规律和机理[9],能够描述宏观疲劳裂纹扩展前,材料内部的损伤演化过程,如Zhang等[10]通过三维有限元法实现了CDM多轴疲劳损伤理论在钛合金中的应用,并验证了其在微动疲劳研究中的有效性;Do等[11]基于CDM疲劳模型和有限元法,考虑残余应力的影响精确预测了对接焊缝高周疲劳寿命.CDM方法可用于研究构件表观形貌对疲劳损伤非线性发展的影响,非常适合实际工程中具有复杂表面特征的锈蚀钢筋的疲劳研究,可以弥补传统疲劳研究方法的诸多不足,但目前鲜有文献关注到CDM模型在坑蚀钢筋高周疲劳分析中的应用.

本文首先引入基于CDM的疲劳损伤模型,然后通过钢筋试件疲劳试验获取模型参数,利用Abaqus用户自定义材料子程序(Umat)编写算法程序,基于加速锈蚀钢筋的蚀坑尺寸建立有限元模型,最后结合坑蚀钢筋疲劳试验进行疲劳寿命预测及疲劳损伤和应力场演化的分析.可以为非均匀锈蚀形态下的钢筋疲劳损伤研究提供参考.

1 连续介质损伤力学模型

循环载荷作用下,各向同性材料的力学性质劣化表现为刚度的下降.定义损伤变量(D)为[9]：

(1)

式中：E为无损伤材料的弹性模量,MPa;ED为有损伤时的等效弹性模量,MPa;D的变化范围为0～1.

根据应变等效原理,耦合损伤的弹性本构关系为：

(2)

式中：v是材料的泊松比;σij和εij分别是应力张量和应变张量;σkk是第一应力不变量；δij是Kronecker符号.

对于高周疲劳,损伤演化法则依赖于循环荷载作用下材料的应力状态和循环次数.Chaudonneret[12]提出了一种适用于多轴应力状态的疲劳损伤演化模型：

(3)

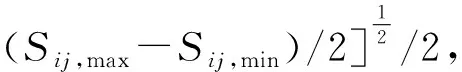
2 疲劳试验

GB 50010—2010《混凝土结构设计规范》推荐使用HRB400钢筋,但目前尚未检索到相关文献中有提出HRB400钢筋材料的CDM模型参数.本文开展HRB400钢筋材料性能试验以获取模型参数,并进行坑蚀钢筋的高周疲劳试验,用以验证本文基于CDM理论的钢筋疲劳有限元模拟.

2.1 参数标定试验

试件由直径20mm的HRB400钢筋加工而成,其化学组成见表1,几何尺寸见图1.

表1 HRB400钢筋化学组成

图1 试件尺寸Fig.1 Specimen size(size:mm)

先通过静态拉伸试验获得试件的极限抗拉强度(σu).3个试件的σu实测值分别为581、586、585MPa,平均值为584MPa.疲劳试验采用长春机械院生产的25t电液伺服疲劳试验机,加载模式采用应力控制的轴向常幅循环加载,加载频率取5Hz.试验分组、加载参数及试件疲劳寿命见表2.其中σmax为最大拉伸应力,σm为平均拉伸应力,Nf为疲劳寿命,Nfm为平均疲劳寿命.

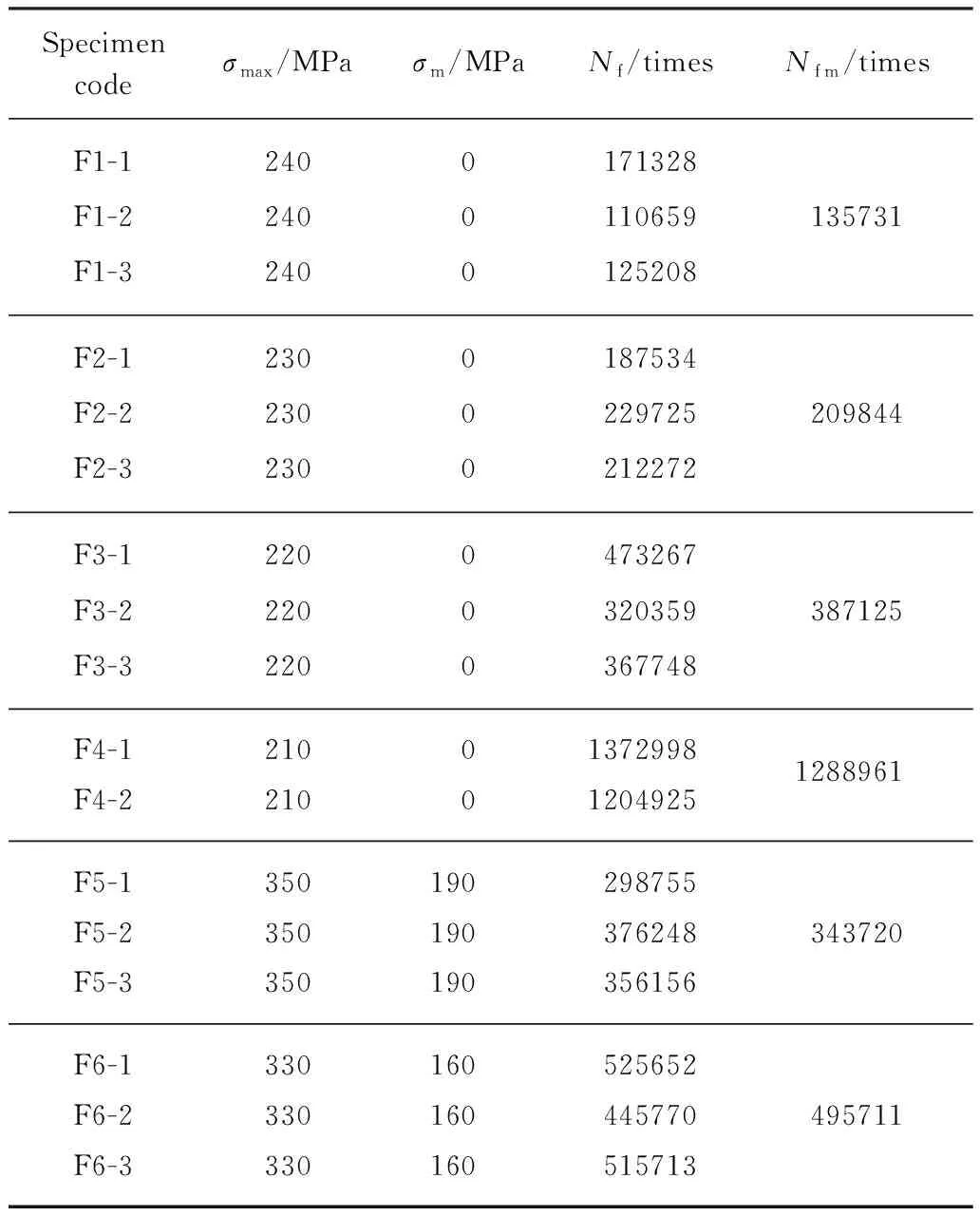
表2 HRB400钢筋试件疲劳试验结果

2.2 坑蚀钢筋高周疲劳试验

采用2.1节所述的钢筋试件,通过外加电流加速

锈蚀的方法制作钢筋蚀坑：先在试件表面紧密缠绕防水绝缘胶带,并在居中位置制作1个椭圆孔,两端用硅酮胶密封防水(见图2);将浸入5%(质量分数)NaCl溶液中的试件作为阳极,不锈钢片作为阴极,连接至直流电源(见图3),电流密度控制为400μA/cm2;通过控制初始椭圆尺寸与通电时间,可以获取不同蚀坑尺寸的锈蚀钢筋试件.

图2 预处理的钢筋试件Fig.2 Pretreated steel bar specimen

图3 加速锈蚀装置Fig.3 Accelerated corrosion setup

通电过程完成后取出试件,用乙酸溶液除去锈蚀产物并用清水洗净,使用游标卡尺测量蚀坑三维尺寸后放置于干燥的密封盒内.蚀坑接近半椭球形,因此采用半椭球模型描述蚀坑形态,本文钢筋锈蚀形貌及半椭球模型的几何参数如图4所示.坑蚀钢筋试件高周疲劳试验的试验设计同2.1节,蚀坑尺寸、加载参数及疲劳寿命见表3.

图4 锈蚀钢筋试件Fig.4 Corroded steel bar specimen

表3 锈蚀钢筋试件的蚀坑尺寸与疲劳试验结果

3 有限元模拟

3.1 材料参数

材料极限抗拉强度取实测均值σu=584MPa,杨氏模量E取210GPa,泊松比v为0.3[13].根据Basquin公式[14]外推的方法,计算钢筋在应力比R=-1情况下的疲劳极限σ10.Basquin公式的对数形式为：

lgNf=Algσa+B

(4)

式中：σa是应力幅值,MPa;σa=σmax-σm,A和B是无量纲材料参数.

根据式(4),对表2中F1～F4组的数据进行线性拟合,得lgNf=-16.62 lgσa+44.61.取应力循环基数为2×106次,即可得到σ10=205MPa.

在疲劳损伤演化法则中,有β、M0、a、b1和b2共5个参数待标定.将损伤演化方程(3)以单轴应力形式[10]积分,得到光滑试件在常幅疲劳荷载作用下的疲劳寿命表达式：

(5)

用表2中F1～F4的试验数据点可拟合得β、aM0-β的值.将F5和F6的试验数据代入式(5),可得到参数b1和b2的值.对于参数a,采用Zhang等[10]提出的数值方法求解.HRB400钢筋的CDM疲劳损伤演化模型参数的取值列于表4.

表4 HRB400钢筋疲劳损伤演化模型的参数取值

3.2 材料子程序算法

由前述模型可知,应力场与损伤场耦合,损伤变量D随着荷载循环而发生非线性的演化,需应用数值算法求解.本文利用Abaqus软件的Umat模块,使用Fortran语言定义材料属性,用于有限元法分析.算法流程图见图5,具体步骤为：

图5 算法流程图Fig.5 Flowchart of the numerical algorithm

(1)初始化材料参数.将损伤初始值设定为0.

(2)调用Abaqus求解器,求解耦合损伤的弹性本构关系式(2),计算出该次循环荷载下每个积分点的应力历程.

(3)计算损伤值,更新循环次数.由于高周疲劳的寿命值较大,若逐次计算所有循环过程,将耗费大量时间.本文采用跳跃式的算法,即假设在ΔN次循环内,损伤值及应力场不变[15].为了保证计算精度,并且节约计算成本,取ΔN的值为疲劳寿命的1%.通过式(3)计算得到损伤演化率dD/dN,更新损伤累积值为D(i+1)=D(i)+(dD/dN)(i)·ΔN,更新循环次数N(i+1)=N(i)+ΔN.

(4)判断是否有积分点的损伤值达到1.如有,则结束程序,输出N(i+1)为疲劳寿命.否则,利用损伤累积值更新材料弹性模量E(i+1)=E(i)·(1-D(i+1)),由此实现材料在循环荷载作用下的力学性能退化,重复步骤(2)、(3),直到有积分点的损伤值达到1.

3.3 有限元模型

根据试件CF1～CF6实测蚀坑尺寸建立有限元实体模型(见图6),模型仅针对试件的有效测试段,不考虑夹持段与过渡段.以试件CF1为例,图6(a)为其有限元模型网格划分,单元类型采用8节点六面体线性实体单元(C3D8).为获得精确的分析结果,在蚀坑处进行网格细分,如图6(b)所示,单元尺寸控制在50～80μm.材料属性调用3.2节所述的Umat子程序.在第1个分析步中施加290MPa的定值轴向均布荷载,在后续分析步中施加最大值为290MPa,应力比0.1的轴向循环应力.其他各试件的有限元模拟过程均类似.

图6 试件CF1有限元模型网格划分Fig.6 Mesh of the FE model of specimen CF1

4 试验与模拟结果分析

4.1 疲劳寿命

将有限元模型提交Abaqus求解器后即可获得坑蚀钢筋的疲劳寿命预测值.为验证本文方法的有效性,收集了王珏[16]与Chen等[17]的试验数据,对适于弹性疲劳损伤分析的试件进行了数值模拟.若使用传统的S-N法[4-5,18]预测疲劳寿命,需要得到与本文各试件相同的锈蚀率和应力比试验数据,且难以考虑蚀坑的影响,故难以进行.因此,本文应用Sun等[7]基于FM法提出的坑蚀钢筋疲劳寿命计算公式,预测了各试件的疲劳寿命,结果如图7所示.其中,实心点为本文CDM模型预测寿命与实测寿命的对比,空心点是FM法预测疲劳寿命与实测寿命的对比,实线表示预测值与试验值相等,虚线表示±0.08的置信区间,相当于约20%(10±0.08)误差的范围.

由图7可见,本文的CDM模型预测坑蚀钢筋高周疲劳寿命与试验基本相吻合,也能够较好地符合文献[16]的疲劳试验结果,但与文献[17]的个别数据有较大偏离,原因可能是试验用钢筋性能存在差异.此外,FM方法亦能较好地预测疲劳寿命,但是当应力比不同时,FM法预测值偏差较多,原因是FM模型参数与蚀坑形态、应力比等相关,而本文方法可考虑锈蚀形态和应力状态的影响,结果也更为准确.由以上分析可知,基于CDM方法预测锈蚀钢筋的疲劳寿命在不同蚀坑尺寸、不同的应力水平下均有良好的适用性.

图7 疲劳寿命预测值与试验值对比Fig.7 Comparison between the predicted fatigue life and the testing data

4.2 疲劳损伤演化

由于蚀坑处存在应力集中,疲劳损伤集中发生在蚀坑底部.图8为有限元计算得到的试件CF1蚀坑表面处损伤分布的变化过程.由图8可见,疲劳前期损伤范围较小,损伤值也很小,疲劳后期可明显观察到疲劳损伤累积,损伤区域从蚀坑底部逐渐向周围扩展.为了定量研究蚀坑损伤分布,以试件CF4有限元计算结果为例,设定以蚀坑底部为起点,沿钢筋轴向(x方向)到蚀坑边沿的路径,图9中红色的节点标记出了该路径.

图8 试件CF1有限元模型疲劳损伤分布Fig.8 Distribution of fatigue damage of specimen CF1 FE model

图9 试件CF4有限元模型路径的定义Fig.9 Path definition of specimen CF4 FE model

图10为不同循环次数下,沿试件CF4路径的损伤值分布.由图10可见：在疲劳中前期,各点损伤值均很小,仅略微大于0;疲劳后期在蚀坑底部附近损伤发展较快,蚀坑底部的节点损伤值先达到1,而距离2mm 之外的节点疲劳损伤发展较慢.这种现象表明,蚀坑加剧了钢筋的疲劳损伤,使钢筋容易形成宏观疲劳裂纹,降低钢筋疲劳寿命.这与试验中钢筋断裂位置在蚀坑底部相符.

图10 不同循环次数下沿试件CF4路径的损伤分布Fig.10 Distribution of damage along the path of specimen CF4 at different number of cycles

提取试件CF1～CF6蚀坑底部处的损伤值随循环次数N的变化,获取其疲劳损伤演化,如图11所示.由图11可见,各试件在疲劳初期的损伤值较低,当循环次数接近疲劳寿命时,疲劳损伤迅速累积,CDM模型的疲劳损伤累积规律是非线性的.

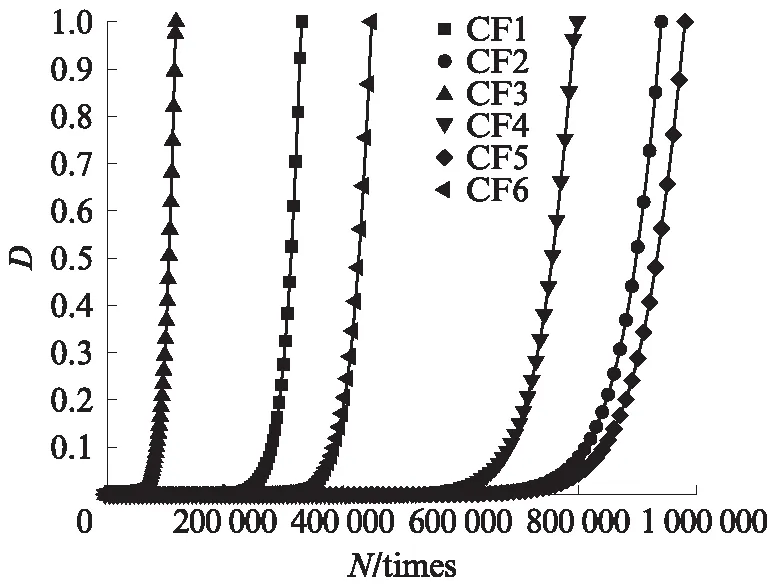
图11 试件CF1～CF6 蚀坑底部的疲劳损伤演化Fig.11 Damage evolution at the bottom of pits of specimen CF1-CF6

4.3 应力场演化

图12为试件CF2在疲劳初期与中后期1次循环中Mises应力最大值(σeq,max)的分布.由图12可见,在疲劳初期,蚀坑部位存在明显的应力集中,由4.2节可知,该处损伤发展也较为集中.因为材料弹性模量随着损伤的累积而逐渐降低,在疲劳后期蚀坑内σeq,max卸载到较低值,如图12(b)、(c)所示.

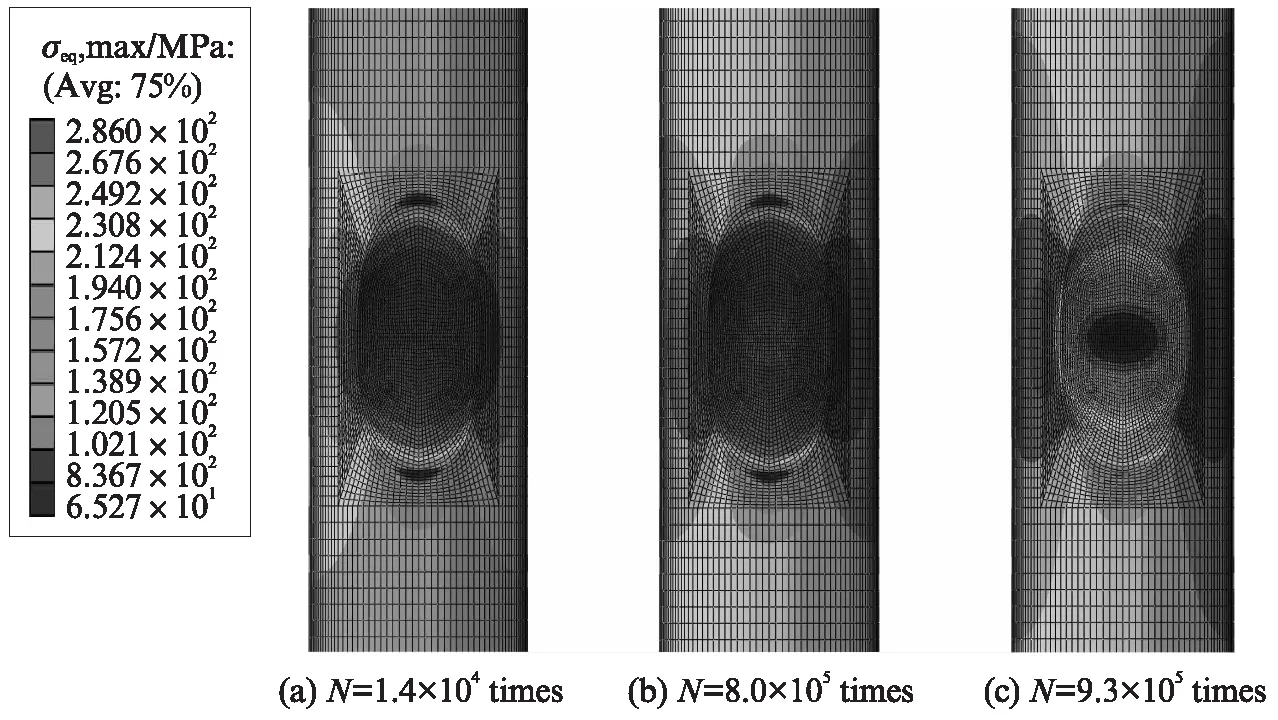
图12 试件CF2有限元模型σeq,max的分布Fig.12 Distribution of σeq,max of specimen CF2 FE model

这体现了在CDM模型中,材料性能随着荷载循环而退化是疲劳失效的重要机理.如图13中红色的节点所示,在试件CF5表面设定以蚀坑底部为起点,沿钢筋环向(y方向)到蚀坑外围的路径,不同循环次数时沿该路径的σeq,max的分布见图14.由图14可见,疲劳中前期蚀坑内σeq,max值均较高,且变化微小;疲劳后期蚀坑部位的σeq,max显著降低,而蚀坑外围区域的σeq,max有所增高,应力重新分布.

图13 试件CF5有限元模型路径的定义Fig.13 Path definition of the specimen CF5 FE model

图14 不同循环次数下沿试件CF5路径的σeq,max分布Fig.14 Distribution of σeq,max along path of specimen CF5 at different number of cycles

图15为试件CF1～CF6蚀坑底部处σeq,max随循环次数的变化.由图15可见：在疲劳中前期,σeq,max略微降低;当循环次数逐渐接近疲劳寿命时,σeq,max迅速降低,在循环次数达到疲劳寿命时降低至接近0值,意味着疲劳失效.CDM模型能够反映高周疲劳破坏的突然性.

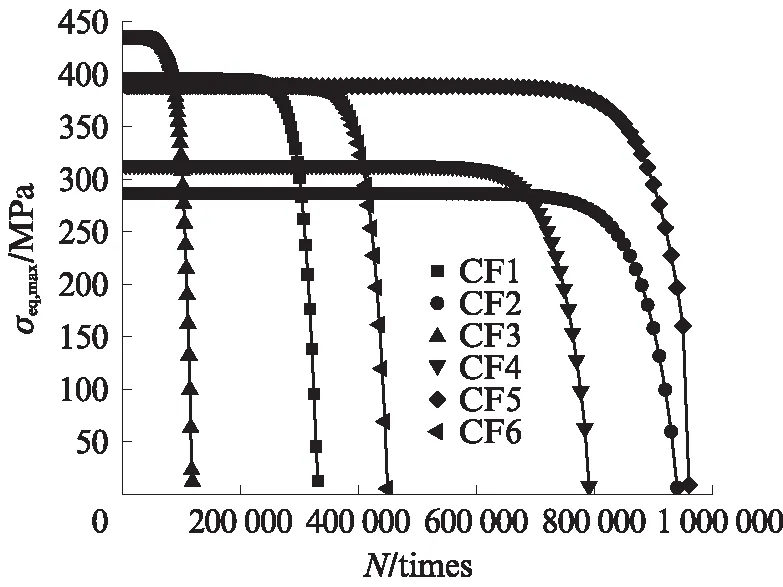
图15 试件CF1～CF6 蚀坑底部的σeq,max演化Fig.15 Evolution of σeq,max at bottom of pits of specimen CF1-CF6

5 结论

(1)将CDM模型引入坑蚀钢筋高周疲劳的研究中,通过钢筋试件疲劳试验和数据分析,标定了HRB400钢筋的CDM模型参数.在Abaqus平台上通过二次开发编写了CDM模型的Umat程序.

(2)CDM模型和Umat算法预测疲劳寿命与试验值吻合较好.应力场和损伤场的演化表明,钢筋蚀坑处应力集中加剧了疲劳损伤发展,疲劳前期和中期损伤发展缓慢,疲劳后期疲劳损伤迅速累积、扩展;由于材料性能退化,蚀坑部位发生了应力重分布,蚀坑底部的应力在疲劳后期迅速卸载,而其外围应力有所升高.

(3)主要考虑了基于弹性损伤的高周疲劳,当蚀坑处因应力集中而达到塑性阶段时,则需要考虑弹塑性疲劳损伤演化.CDM方法适用于不同蚀坑尺寸和不同应力水平下坑蚀钢筋的疲劳分析,具有良好的应用前景.