基于LCL-S的恒压恒流切换无线电能传输系统
张 奇 杨云虎 张 杨 邓泽卓
(安徽工业大学电气与信息工程学院/安徽省高校电力电子与运动控制重点实验室, 安徽 马鞍山 243000)
与传统的有线接触式电能传输系统相比,无线电能传输系统(Wireless Power Transfer,WPT)具有非接触操作、应用方便、安全可靠等优点[1-3]。电动汽车制造中最常用的电池是锂离子电池,其充电过程中的安全性非常重要。在电动汽车充电过程中,恒流(Contant Current,CC)和恒压(Contant Voltage,CV)的充电模式占主导地位。电池开始充电时以恒流模式运行,当负载等效电阻增大到临界点时切换到恒压模式运行,此后则以恒压模式充电[4-5]。
有研究指出,恒压、恒流输出的实现,可以采用在发射侧引入闭环回路的方法,对负载电压或者电流进行检测并将数据反馈到控制系统,调节输出信号的占空比[6-8]。但是发射侧与接受侧的控制过程较复杂,有的甚至需要在接受侧增加BUCK电路,使系统损耗上升。另一种实现恒压恒流的方法,是改变补偿拓扑结构,配置不同的参数。另有文献中提出的串串-串并拓扑结构[9]和 LCC-LCC、LCC-S 混合变拓扑结构[10],都可实现恒流输出和恒压输出。其缺点是,需要在变拓扑结构中加入多个补偿元件,不仅电路设计相对复杂,而且装置体积偏大。
基于以上问题,本次研究将设计一种在发射侧具有辅助电容的LCL-S补偿拓扑无线电能传输系统。LCL结构具有恒流恒压特性[11],但单一拓扑参数只可获得一种固定的传输特性,无法同时实现恒流和恒压两种模式。发射侧的单个交流开关用于配置补偿拓扑,只有发送端信息用于配置补偿拓扑,因此,并不依赖无线通信。该拓扑结构的优点是,在固定频率下工作,控制方案简单。
1 系统工作原理
1.1 电路拓扑


(1)
Zin为图1中从发射侧看过去的输入阻抗:
(2)
其中Zr为图1中接受侧在发射侧的反射阻抗。
(3)
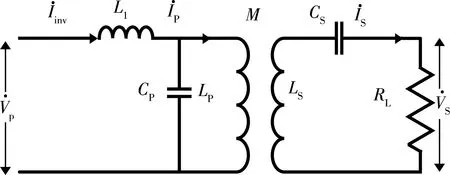
图1 LCL-S等效分析模型
1.2 恒流模式


图2 CP被分割的LCL-S等效电路模型
式(4)中,ω0为谐振频率:
(4)

(5)

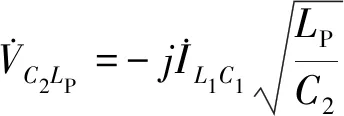
(6)


(7)
根据式(7),可知等效的电流源大小与原边电压和两个电感值有关。变换式(7),可得到次级线圈中的电流:
(8)
根据式(8)可知,接收线圈的输出电流与负载无关。当发射端和接收端发生谐振时,根据式(9)计算恒流模式下的输入阻抗:
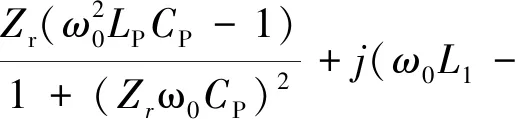
(9)

1.3 恒压模式分析
分析LCL-S补偿拓扑独立于负载的输出电压。L1=LP作为输入侧实现零相角(ZPA)条件,有式(10)(11)(12)。
(10)

(11)
(12)
由式(12)可知,流过发射线圈的电流与负载无关。据式(13)计算接收侧负载两端的电压:
(13)
由式(13)可知,负载电压与负载无关。由式(14)可知,逆变电流与互感有关。
(14)
据式(15),计算恒压模式下的输入阻抗:
(15)
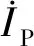
2 系统整体设计
本次研究提出的无线充电拓扑结构如图3所示。为了处理双向谐振电流,将Sp设为两个IGBT的反并联连接。在恒流工作模式下,SP处于导通状态,然后L1和LP与发射侧的两个电容产生谐振,而LS与接收侧的电容产生谐振。在恒压模式下,SP处于关闭状态,然后L1与发送侧的电容产生谐振,LS与接收侧的电容产生谐振。

图3 LCL-S可重构的无线充电拓扑
逆变器的输出电压VP可由逆变器以直流电压E的50%占空比进行调节。一次谐波分量的输出电压幅值可用式(16)表示:
(16)
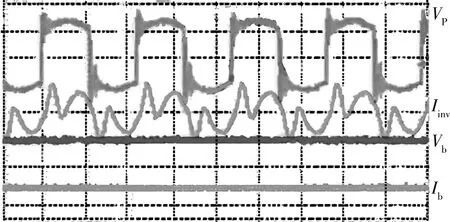
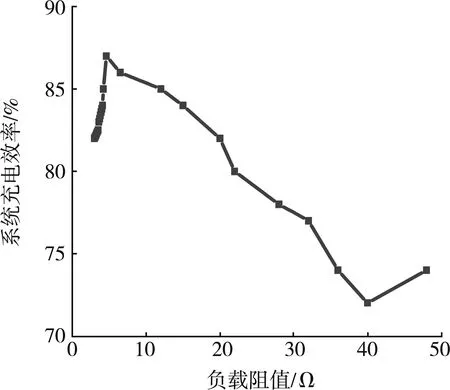
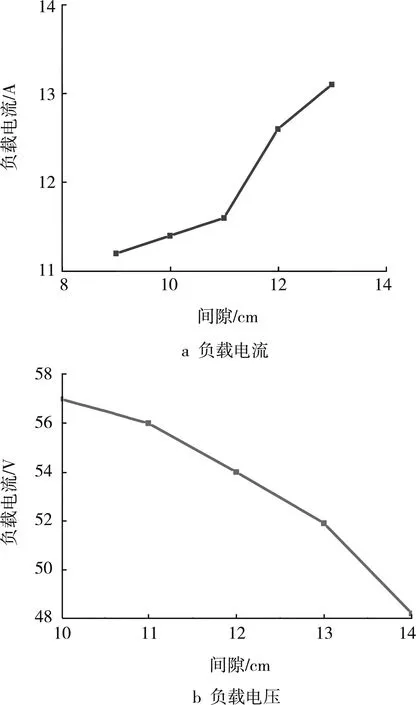
图4给出了开关SP的控制逻辑,其中Vref为在恒压充电模式下的参考电压。将预估的电池电压Vb与参考电压Vref进行比较:当Vb 在系统设计中,必须考虑电池恒流充电模式下的额定电流(12 A),即Ib此时为12 A和额定电压(56 V)即Vb为56 V。额定条件下电池的等效电阻(R0)用式(17)计算: (17) 整流器输入端的等效电阻RL用式(18)计算: (18) LS通过接收端负载的品质因数(QS)来计算,如式(19): (19) QS取值为4,LS在85 kHz频率下的评估值为28.5 μH。VS的有效值可用式(20)计算: (20) 由式(20)计算出IS的有效值为13.3 A。通过式(15)找到M,恒压模式下考虑耦合系数为0.23,VP有效值为230 V。移相调制技术用于控制高频逆变器的输出电压。 图4 Sp控制逻辑 图5所示为S1— S4的相关栅极脉冲和相移调制技术的逆变器输出电压。在恒压模式下,当VP的有效值为23 V时,最大相移为180°,则得到E为255.5 V。对于恒流模式,计算出VP为50 V。保持恒定的E(恒压模式),在VP有效值为50 V时,移相角必须改为27°。 为了使设计更简单、制造成本更低,线圈采用了圆形螺旋线圈几何形状。接收线圈的外径(Do)设为40 cm。发射线圈的外径为42 cm,发射线圈和接收线圈之间的间隙为12 cm。圆形螺旋线圈的自感系数可以用惠勒公式计算,如式(21): (21) 圆形螺旋线圈不同参数之间的数量关系如式(22)所示: Do=Di+2(N-1)(td+r)+2r (22) 通过式(21)(22),可确定发射线圈、接收线圈的不同参数。利兹线的直径为2.58 mm,发射线圈的匝数为6、内径为40 cm 、匝间距为0.2 cm,接收线圈的匝数为6、内径为38 cm、匝间距为0 cm。 图5 S1 — S4相移控制 通过实验验证拓扑结构的有效性。实验元件相关参数如表1所示。 表1 实验元件参数 恒流模式下的输出电流为12 A,恒压模式下的输出电压为56 V。通过数字信号处理器(DSP) TMS320F28335实现控制,在恒流、恒压模式中计算相移。实验样机由直流电压源、高频逆变器、松耦合变压器、发射侧补偿电容、接收侧补偿电容、接收侧补偿电感、全桥整流器、可变负载、示波器组成。其中,高频逆变器由4个具有较低导通电阻的 MOSFET 构成,全桥不可控整流器由4个快恢复二极管构成。 通过实验,验证不同负载下实现恒流输出和恒压输出的特性。图6、图7中自上往下:第一通道表示输入电压VP;第二通道表示逆变电流Iinv;第三通道表示负载电压Vb;第四通道表示负载电流Ib。横坐标每一格的间隔为5 μs。当工作频率为110 kHz时,直流输入电压为220 V。当负载电阻为3.4 Ω时,逆变器的输出和负载电压、电流如图6所示,即恒流模式。第四通道是负载电流Ib,其输出电流等于11.5 A时,接近我们需要得到的值。 由于输入阻抗角较小,系统需要以较小的无功功率确保在逆变器开关接通期间保持软开关状态。当负载电阻为15 Ω时逆变器输出和负载电压、电流如图7所示,即恒压模式。第三通道是负载电压Vb,输出电压为54 V时,约等于恒压模式下电压的参考值。 对于不同的电阻值,在整个充电过程中的系统效率曲线如图8所示。随着负载发生变化,最大充电效率(87%)发生在恒流到恒压模式转换期间,此时等效电阻为6 Ω。恒流向恒压模式切换时输出电压发生跳变,输出电流保持恒定,达到恒压状态时输出电流开始减小,输出电压基本不变。 图6 恒流模式下的实验波形 图7 恒压模式下的实验波形 图8 系统充电效率曲线 针对电动汽车的静态充电问题,研究人员开发了经济高效的停车辅助系统,可用于调整车辆位置[12-13]。此外,一旦线圈系统被设计用于特定的车辆离地间隙,该特定车辆线圈系统的距离变化是由于车轮中气压变化所引起。此变化较小,所以互感M可以保持近似恒定。 此外,通过实验研究了气隙距离和互感M的变化对输出电流、电压的影响。对于10~14 cm的间隙变化,互感M则在7.5~6.21 μH之间变化。从图9可以看出间隙变化对输出电流、电压的影响。对于11~12 cm的间隙距离范围,输出电流的变化小于2%,输出电压的变化小于 2%。 图9 线圈间隙变化对输出的影响 本次研究设计的磁耦合谐振式无线充电系统,是在LCL变参数补偿基础上,通过改变补偿参数来实现与负载无关的恒压、恒流输出。通过LCL-S拓扑原副边来建立模型,在发射侧使用辅助电容器来重新配置补偿拓扑。其中,恒流模式可以实现ZVS,恒压模式可以实现ZPA。该系统能输出不受负载变化影响的恒定电流和恒定电压,实现恒压恒流充电以及两种模式的切换,最大充电效率可达到87.5%。 系统中,将恒流输出和恒压输出融入到一个拓扑中,但是需通过一侧增加交流开关来实现。在开关切换过程中,会出现电池充电电压发生跳变的现象,影响电池寿命。这一点仍有待改进。

3 实验结果分析


4 结 语

