减轮SKINNY-128-384 算法的中间相遇攻击*

肖钰汾, 田 甜

战略支援部队信息工程大学, 郑州450001

1 引言

当前, 随着通信、计算机技术的迅速发展, 分组密码得到广泛应用. 而近十年, 随着物联网的发展, 轻量级密码算法的需求越来越大, 为适应于各种应用环境, 学术界提出一批轻量级分组密码算法. SKINNY算法是由Beierle 等人在2016 年美密会上提出的一种基于SPN 结构的可调轻量分组密码算法[1], 该算法在软硬件实现方面具有较高的效率, 同时也具备较强的安全性. 近两年, 针对SKINNY 算法的安全性分析越来越多, 例如不可能差分攻击[2–4], 截断不可能差分攻击[5], 零相关线性攻击[6]和中间相遇攻击[7]等. 对减轮SKINNY 算法, 已有学者提出了22 轮SKINNY-128-384 的中间相遇攻击以及其改进的相关结果[7,8]. 中间相遇攻击对SKINNY 算法是一种效果比较显著的攻击方法.

中间相遇攻击的思想最早由Diffie 和Hellman 在1977 年提出并应用到分组密码DES 的安全性分析中[9], 后来这一攻击方法在AES 算法等SPN 结构的分组密码中得到广泛应用. AES 的中间相遇攻击最早是由Demirci 和Selçuk 在2008 年Fast Software Encryption (FSE) 会议上提出[10], 他们沿用了Diffie 和Hellman 的基本思想, 改进了Gilbert 和Minier 给出的三轮AES 加密输入和输出之间映射关系的性质[11], 提出了AES 的四轮中间相遇区分器, 以及在单密钥下7 轮AES-192 和8 轮AES-256 的攻击结果. Demirci 和Selçuk 提出的中间相遇攻击被称为DS-MITM, 普遍认为是SPN 结构分组密码最经典的中间相遇攻击. 文献[12–15] 对Demirci 和Selçuk 的AES 中间相遇攻击算法进行了改进, 形成了许多在中间相遇攻击中常用的技术方法, 例如文献[12] 提出的多重集技术、密钥桥技术和差分枚举技术. 文献[15] 对10 轮AES-256 算法的中间相遇攻击进行了理论分析, 是目前为止针对AES 算法轮数最长的中间相遇攻击. 文献[7] 和[16] 提出了中间相遇攻击的自动化搜索技术, 尤其是[7] 中所给出的DS-MITM自动化搜索模型形成了中间相遇攻击一般化的搜索方式, 为快速有效地给出SPN 结构分组密码算法最优的中间相遇区分器和攻击方案提供了一种新的途径.

SKINNY 作为一种典型的SPN 结构的分组密码算法, 其中间相遇攻击的分析过程可采用DS-MITM自动化搜索模型. 文献[7]将中间相遇攻击的自动化搜索模型应用于SKINNY-128-384 中,结合SKINNY算法在列混合过程中可利用的约束条件, 通过自动化搜索的方法, 作者给出了10.5 轮SKINNY-128-384的中间相遇区分器, 并给出了22 轮SKINNY-128-384 的中间相遇攻击. 然而, 文献[7] 所给出的中间相遇攻击并非最优算法,在建立中间相遇区分器的过程中仍有改进的空间. 文献[8]对22 轮SKINNY-128-384的中间相遇攻击进行了改进, 通过建立SKINNY 算法密钥桥的自动化搜索模型, 找到了攻击过程中使得密钥猜测量最少的中间相遇攻击算法, 将在线攻击阶段的时间复杂度降低了216, 然而一定程度上增大了存储复杂度.

本文对史丹萍等人提出的SKINNY 中间相遇区分器进行了一定改进. 在SKINNY 中间相遇区分器的搜索过程中, 本文将不使用列混合的约束条件, 而是考虑将状态的猜测转化为密钥的猜测, 并结合密钥桥技术, 以减少中间相遇区分器的建立过程中密钥的猜测量, 从而降低中间相遇攻击的离线存储复杂度.最终, 我们在不增大时间复杂度和数据复杂度的前提下, 将22 轮SKINNY-128-384 算法中间相遇攻击的离线存储复杂度降低了224.

本文结构安排如下: 第2 节简要介绍SKINNY 算法和史丹萍等人提出的SKINNY 中间相遇攻击;第3 节给出了SKINNY 算法改进后的中间相遇区分器, 并形成了中间相遇攻击的基本过程. 第4 节是对本文的小结.

2 准备工作

2.1 SKINNY 算法介绍

SKINNY 算法由Christof Beierle 等人在2016 年美密会上提出[1], 是一种分组长度和密钥长度可调的轻量级分组密码. SKINNY 算法的分组长度有64 比特和128 比特两种类型, 在这两种分组长度类型中, 每个分组均看作4×4 的方阵. 当分组长度为64 比特时, 单元格数据类型为半字节; 当分组长度为128比特时, 单元格的数据类型为单字节. 记SKINNY 的分组长度为n 比特, SKINNY 的密钥长度可以为大于等于n 且小于等于3n 的任意比特长度. 在加密过程中, 采用Tweakey 的输入模式. Tweakey 的长度记为t, 有三种取值情形, 分别为t = n, t = 2n, t = 3n. SKINNY-n-t 表示分组长度和Tweakey 长度分别为n 和t 的加密版本. 根据分组大小和Tweakey 的不同长度, 加密算法的轮数也不同, 二者与加密轮数的关系如表1所示.

表1 SKINYY-n-t 算法的迭代轮数Table 1 Number of rounds for SKINNY-n-t

2.1.1 加密算法

已知明文m=m0||m1||m2||···||m15. 对于1 ≤i ≤15, 当分组长度为64 比特时, mi的长度为4 比特; 当分组长度为128 比特时, mi的长度为8 比特. 记单元格的比特长度为s.

按照行的顺序, 依次将明文m = m0||m1||m2||···||m15输入到4×4 的矩阵中, 记第i 轮的输入状态分组为Si, 状态矩阵如下所示:

SKINNY 算法的轮函数包含五个步骤的操作, 依次为S 盒替换、轮常数加、轮密钥加、行移位、列混合, 如图1 所示.

图1 SKINNY 加密算法的轮函数Figure 1 Encryption round function of SKINNY

S 盒替换(SC): 对一个分组中的16 个单元格分别进行S 盒替换, 不同分组长度使用的S 盒规模不同. 分组长度为64 时, 采用4 比特规模的S 盒; 分组长度为128 时, 采用8 比特规模的S 盒.

轮常数加(AC): 将状态分组与轮常数矩阵异或加, 其中每一轮的轮常数通过LFSR 来更新.

轮密钥加(ART): 给定Tweakey 输入tk. 当Tweakey 的长度t=n 时, 令tk=tk0||tk1||···||tk15,按行的顺序, 依次将tk0,tk1,··· ,tk15输入4×4 矩阵TK1 中; 当t = 2n 或3n 时, 以相同的方式依次将tk 每16s 比特输入矩阵TK1、TK2 和TK3 中. 进行轮密钥加时, 将Tweakey 矩阵的前两行与状态异或, 即

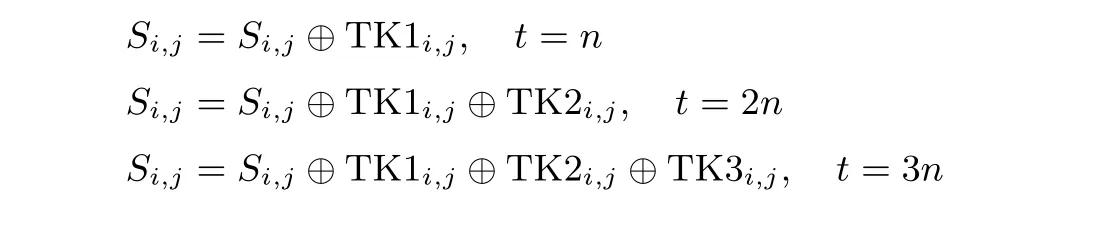
其中, i=0,1, j =0,1,2,3.

行移位(SR): 状态分组的第0,1,2,3 行依次循环右移0,1,2,3 单元格.

列混合(MC): 在状态分组前乘矩阵

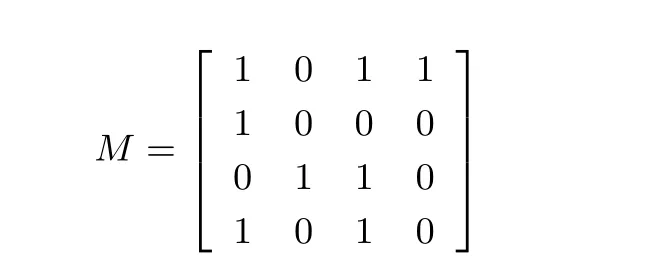
其中运算规则为异或运算.

2.1.2 密钥扩展算法

SKINNY 算法的轮密钥更新即TK1、TK2 和TK3 的更新. TK1 的更新过程为矩阵单元格的置换,即

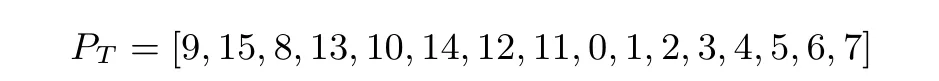
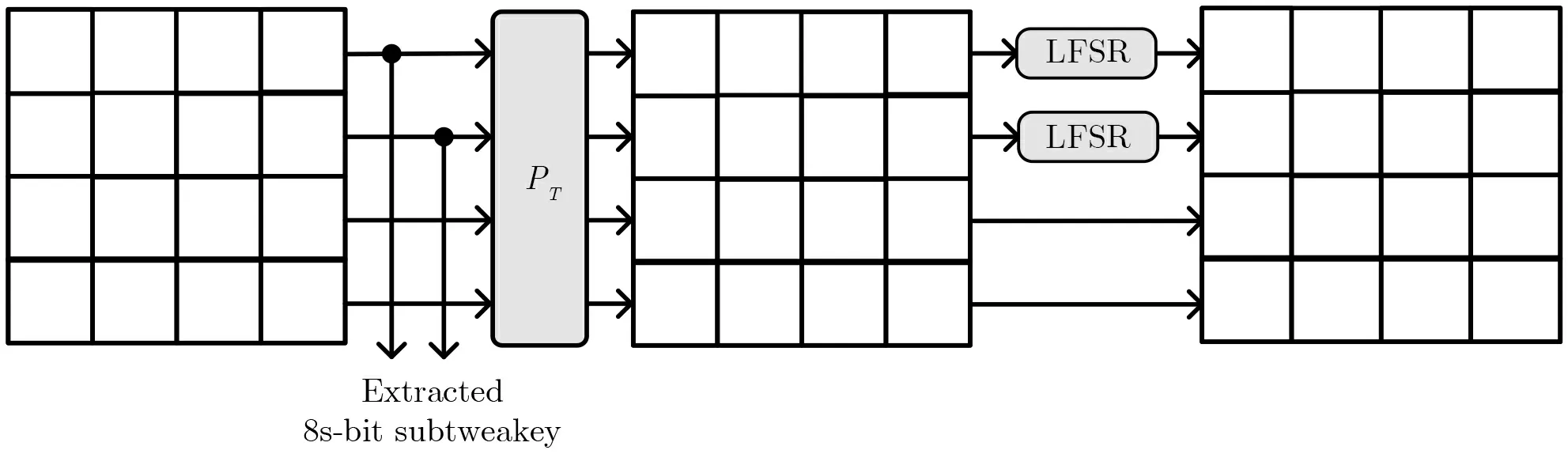
图2 SKINNY 算法中的Tweakey 扩展算法Figure 2 Tweakey schedule in SKINNY

TK2 和TK3 的更新过程如图2 所示, 其中, 置换PT与TK1 的置换一致. LFSR 的更新过程如表2 所示.

表2 Tweakey 扩展算法中LFSR 的更新函数Table 2 Update functions of LFSRs used in Tweakey schedule

2.2 Demirci-Selçuk 中间相遇攻击

2008 年, Demirci 和Selçuk 提出针对AES 分析的中间相遇攻击, 按照其模型所建立的中间相遇攻击一般称为DS-MITM[10], 后续中间相遇攻击的研究均与DS-MITM 有紧密联系. 在DS-MITM 的分析过程中, 首先将加密算法Ek拆分为如图3 所示的三个部分E0,E1和E2, 即Ek= E2◦E1◦E0, E0为加密算法的第0 轮至第r0−1 轮; E1为加密算法的第r0轮至第r0+r1轮, 是中间相遇攻击的区分器部分;E2为加密算法的第r0+r1+1 轮至第r0+r1+r2轮.

图3 DS-MITM 基本模型Figure 3 Basic model of DS-MITM

以下给出DS-MITM 的基本攻击原理.

首先介绍δ-集的概念. 取N 个不同的状态分组或明文分组, 这N 个分组满足在其中一个或者多个单元格中穷尽所有可能值, 这样的单元格称为活跃单元格. 除活跃单元格外, N 个状态分组在其余单元格差分均为0, 则称这N 个状态分组为δ-集.

在图3 的模型中, E1为构建的中间相遇区分器部分. 在构建区分器时, 需要先确定δ-集的活跃单元格以及区分器的输出单元格位置; 根据δ-集在第r0轮至第r0+r1轮的差分传播路径, 以及输出单元格自第r0+r1轮至第r0轮的差分传播路径, 猜测两条路径在传播过程中每一轮输入相交的状态值, 穷尽相交状态的所有取值, 在第r0+r1轮可得到不同的关于输出状态或差分的集合, 将输出集存储在表中, 构成中间相遇区分器. 选取足够的明文, 使得当E0部分的轮密钥值任意猜测时, 在第r0轮的输入状态总能形成一个δ-集. 筛选在第r0轮的输入状态形成δ-集的明文集, 加密生成密文, 猜测E2部分的轮密钥, 部分解密密文, 求得第r0+r1轮输出固定单元格的状态或差分, 判断状态或差分值是否在区分器的存储表中; 若在, 则判断E0和E2部分所猜测的密钥为正确密钥; 否则为错误密钥. 最后通过穷尽剩余密钥的方法, 可筛选出正确密钥.

2.3 史丹萍等人对SKINNY 算法的中间相遇分析

文献[7] 利用DS-MITM 基本模型, 通过自动化搜索的方法, 对SKINNY-128-384 进行了中间相遇分析, 找到10.5 轮的中间相遇区分器, 并给出了22 轮的中间相遇攻击.

此时, 状态的猜测量大于算法SKINNY-128-384 的密钥长度. 根据文献[7], 运用SKINNY 加密算法关于列混合的约束条件, 在一定程度上可以减少上述分组状态字节的猜测量. 记列混合前的状态为Q, 列混合后的状态为Q′, 则SKINNY 的列混合变换可以用以下四式表示:

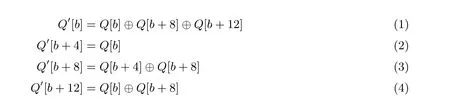
其中b ∈{0,1,2,3}. 将式(1)与式(4)相加, 式(2)与式(4)相加, 得:

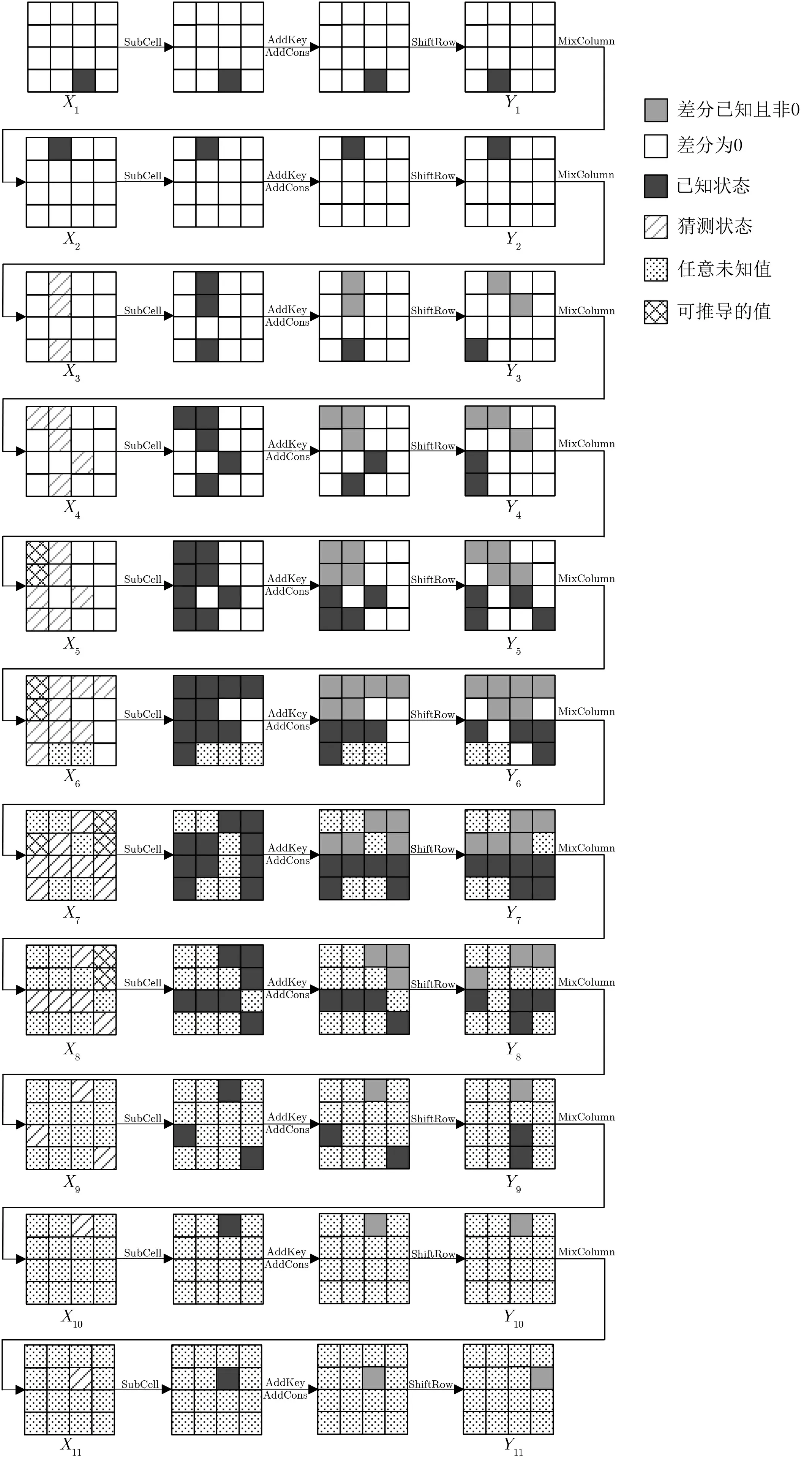
图4 文献[7] 中10.5 轮SKINNY-128-384 的中间相遇区分器Figure 4 MITM distinguisher of 10.5-round SKINNY-128-384 in Ref. [7]

由式(5)和式(6)的约束条件, X5[0,4],X6[0,4],X7[3,4,7],X8[3,7] 可根据已猜测的其它字节以及上一轮已知的部分状态求出. 增加约束条件后, 建立区分器所需猜测的状态值为40 字节.

在区分器前添加3 轮, 区分器后添加8.5 轮, 可以形成22 轮SKINNY-128-384 的中间相遇攻击.攻击过程中选择明文量为296个明文分组, 需要猜测的密钥量为47 字节. 因此, 文献[7] 中对22 轮SKINNY-128-384 的中间相遇攻击, 数据复杂度为296选择明文(CP), 存储复杂度约为2328字节, 时间复杂度约为2382次22 轮SKINNY-128-384 加密.

3 SKINNY-128-384 算法改进的中间相遇攻击

在文献[7] 基础上, 本节讨论SKINNY-128-384 算法中间相遇攻击的改进, 主要降低了文献[7] 对SKINNY 算法攻击的存储复杂度.

3.1 SKINNY-128-384 算法改进的中间相遇区分器

SKINNY 加密算法在轮密钥加的过程中, 每个状态分组仅有前两行参与了轮密钥加的运算, 后两行进行轮常数加. 因此, 在进行中间相遇分析的过程中, 后两行为已知状态. 本文对10.5 轮SKINNY-128-384中间相遇区分器的改进, 主要体现在将推导过程中部分分组状态的猜测转化为部分轮密钥的猜测. 而在轮密钥的猜测过程中, 可以通过密钥桥技术, 找到密钥之间存在的一些关系, 减少密钥的猜测量, 从而一定程度上降低建立区分器过程中的时间复杂度, 也降低了中间相遇攻击的存储复杂度, 同时也提升了在线攻击阶段密钥的过滤效果.

3.1.1 结合状态和密钥的猜测自动化搜索中间相遇区分器

以下用一个例子对一轮变换过程中同时猜测密钥和状态进行简要说明.

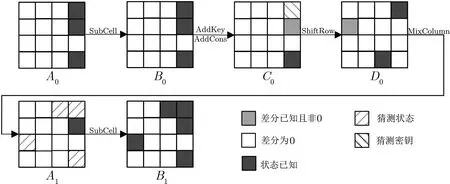
图5 状态与密钥猜测过程示例图Figure 5 Example for guessing roundkey values instead of state values

下面采用文献[7] 提出的自动化搜索模型, 结合以上将部分状态的猜测转化为密钥猜测的方法, 搜索SKINNY-128-384 算法的10.5 轮中间相遇区分器.

在搜索区分器的过程中, 需要引入三组变量集, 依次为Vars(D),Vars(S) 和Vars(F).

Vars(D) = {Di[j],Di[j] ∈0,1,i = 1,··· ,11,j = 0,··· ,15}. 初始值D0[j],j = 0,··· ,15, 由δ-集决定. 在第1 轮到第10 轮的差分传播路径中, 每一轮的输入状态Xj处的差分值决定了Di[j] 的取值. 当所有状态与第0 个状态对应的差分皆为0 时, Di[j] 的取值才能为0; 否则Di[j] 的取值为1.

Vars(S) = {Si[j],Si[j] ∈0,1,i = 1,··· ,11,j = 0,··· ,15}. Vars(S) 的初始值为S11[j],j =0,··· ,15, 值由区分器的输出决定. 在第11 轮到第1 轮的传播路径中, 前后状态的关系决定了Si[j] 的取值. 当第i 轮第j 字节状态已知时, 才能求得第i+1 轮的差分, 则Si[j] 的取值为1.

Vars(F) = {Fi[j],Fi[j] ∈0,1,i = 1,··· ,11,j = 0,··· ,15}. 当Di[j] 和Si[j] 在取值同时为1 时,Fi[j] 的取值才为1; 否则取值为0. 集合Vars(F) 中取值为1 的状态位即为区分器中需要猜测的状态字节单元.

在给定δ-集和区分器的输出字节位置后, 根据Vars(F) 的值, 以及状态与密钥的转化关系, 最终可以确定所需猜测的状态和密钥. 若状态和密钥猜测的字节总数小于48, 则可以构成10.5 轮SKINNY-128-384 的中间相遇区分器.

根据以上方法, 穷尽给定δ-集的活动位置和区分器的输出单元位置, 自动化搜索10.5 轮SKINNY-128-384 的中间相遇区分器. 在搜索结果中, 区分器的输入或输出取两个字节时, 猜测的字节数量普遍较多, 因此此处仅列出区分器的输入仅1 个字节处为活动S 盒, 输出也仅考虑一个字节的情况. 可得出如表3 所示状态和密钥猜测数量的情况.

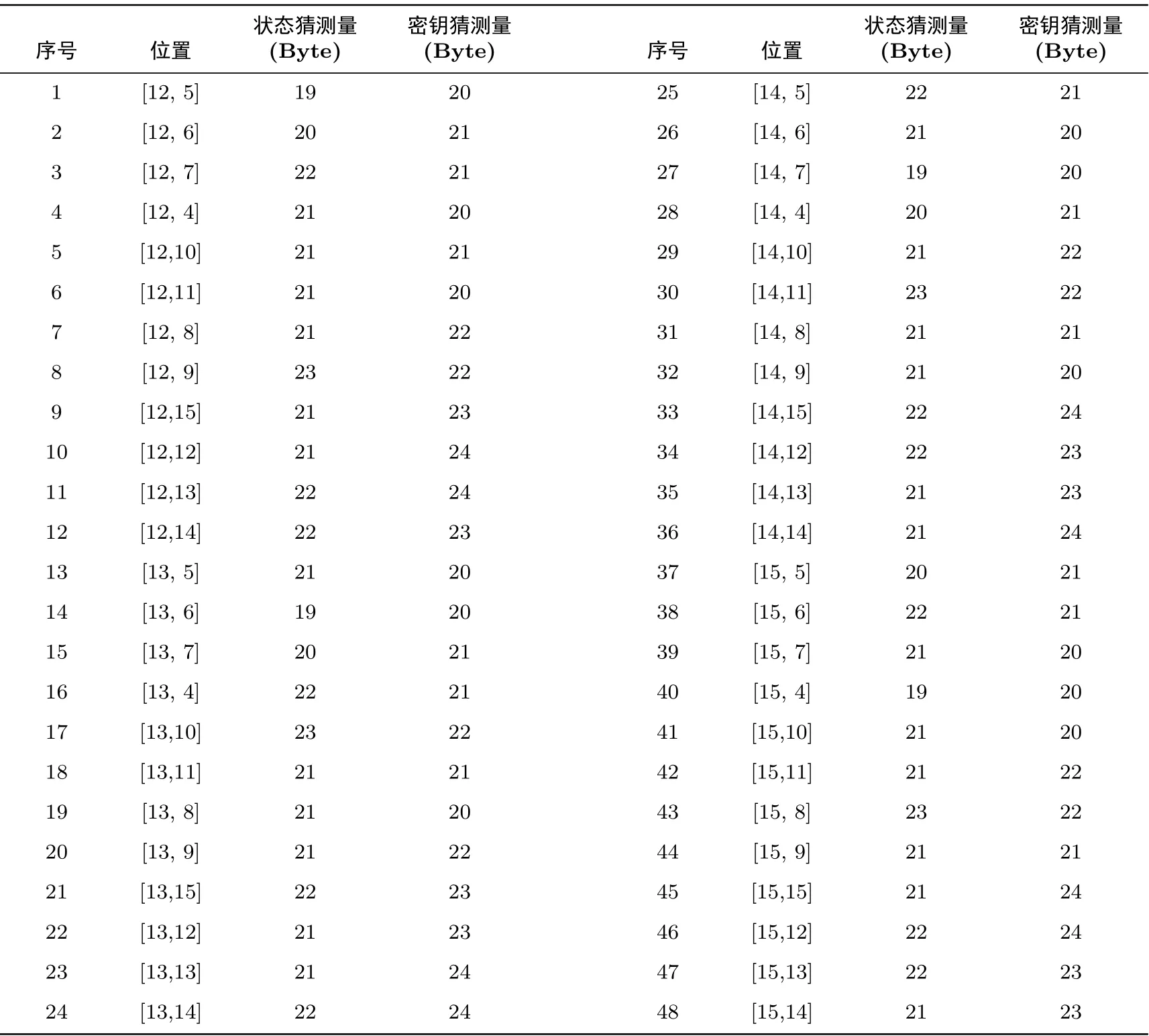
表3 SKINNY-128-384 算法10.5 轮中间相遇区分器以及猜测状态和密钥字节数量Table 3 DS-MITM distinguishers of 10.5-round SKINNY-128-384 with number of guessing state bytes and key bytes

根据表3 的搜索结果, 可以找到四种情况下, 状态猜测量为19 字节, 密钥猜测量为20 字节, 均是表3 中最优的结果. 这四种情况依次为:

(1) 区分器的输入集在第12 字节为活动字节, 输出取第5 字节;

(2) 区分器的输入集在第13 字节为活动字节, 输出取第6 字节;

(3) 区分器的输入集在第14 字节为活动字节, 输出取第7 字节;

(4) 区分器的输入集在第15 字节为活动字节, 输出取第4 字节.

根据SKINNY-128-384 的轮密钥扩展算法, 结合密钥桥技术, 当区分器输入集在第12 字节为活动字节, 输出取第5 字节时, 可将密钥的猜测量降低2 个字节. 其余三种情况均无法达到相同效果.

3.1.2 利用密钥桥技术确定最优中间相遇区分器

密钥桥技术在文献[12] 中被提出, 用于AES 的中间相遇攻击. 根据AES 算法轮密钥之间的线性关系, 可在攻击过程中降低轮密钥的猜测量. 后来, 密钥桥技术在分组密码的中间相遇分析以及其他各类密码分析中得到了广泛应用, 也有学者将自动化搜索的方法用于密钥桥技术中[17]. SKINNY 算法轮密钥的扩展主要通过置换和字节内部移位寄存器的线性变换实现. 在寻找SKINNY 算法轮密钥之间的关系时,也可以通过自动化的方法进行搜索, 由于只需考虑置换关系, 因此搜索过程也较简单.

下面结合密钥桥技术, 给出10.5 轮SKINNY-128-384 改进后的中间相遇区分器.

根据性质2, 建立SKINNY-128-384 的10.5 轮中间相遇区分器, 需要确定37 个字节的数据量, 建表所需要的存储复杂度为28×37×255 ≈2304字节.

3.2 SKINNY-128-384 算法改进的中间相遇攻击

针对SKINNY-128-384 的单密钥恢复攻击, 可以在10.5 轮区分器之前添加3 轮, 后面添加8.5 轮,如图7 所示, 形成22 轮的中间相遇攻击, 具体攻击流程如下所述.

离线预存储阶段: 猜测上述10.5 轮区分器中37 字节状态和密钥, 穷尽2296个状态, 得到2296个多重集, 并将多重集存储在表T 中.

在线攻击阶段:

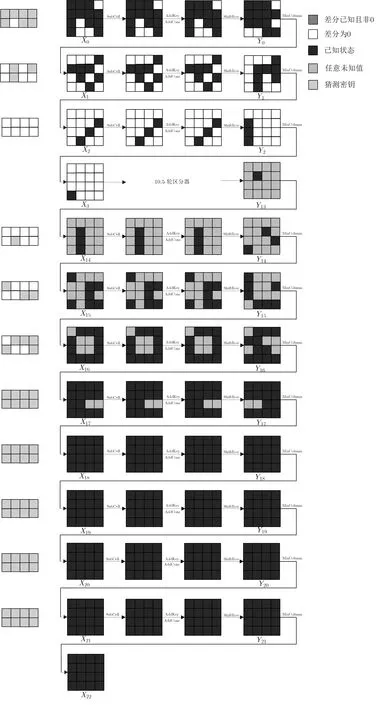
图7 22 轮SKINNY-128-384 算法的中间相遇攻击Figure 7 MITM attack for 22-round SKINNY-128-384

(1) 选择296个明文, 这些明文满足在第3, 9, 13, 14 字节处差分为0, 其余12 字节穷尽即可;

(2) 猜测第0,1,2 轮的部分轮密钥RK0[0,1,2,3,4,6,7],RK1[1,3,5], 筛选一对明文, 使得这对明文在第3 轮输入状态X3处满足差分仅在第12 字节非0, 取这对明文之一, 记为P0;

(3) 根据δ-集的性质,以及上述猜测的轮密钥,可反解P1,P2,··· ,P255,并用22 轮SKINNY-128-384加密这256 个明文, 得256 个密文;

(4) 如图7, 左侧阴影部分为需要确定的第14 至21 轮部分轮密钥, 即

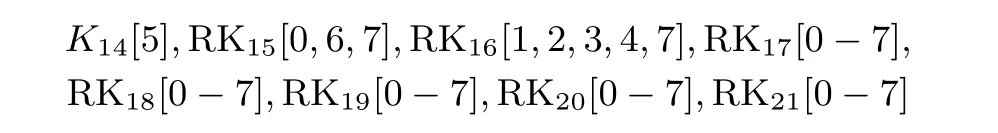
确定这些位置的密钥值后, 部分解密256 个密文, 求得Y13[5], 计算差分集

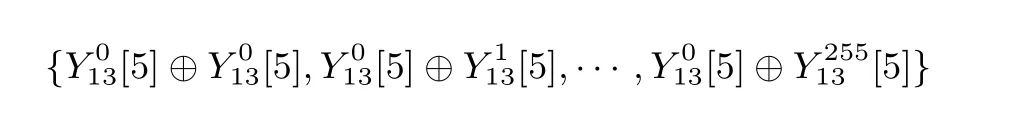
(5) 判断差分集是否在离线阶段建立的存储表T 中. 若在, 则判断猜测的密钥为正确密钥; 否则, 判为错误密钥;

(6) 通过穷尽搜索的方式筛选出正确密钥.

上述攻击步骤中, 需要确定的轮密钥共有59 个字节. 依据密钥扩展算法中的置换关系, 结合如图8 所示的密钥桥技术, 可以将轮密钥的猜测转化为如下Tweakey 和轮密钥的猜测:

由此, 可得22 轮SKINNY-128-384 算法的中间相遇攻击在线阶段所需要猜测的密钥量为47 字节.

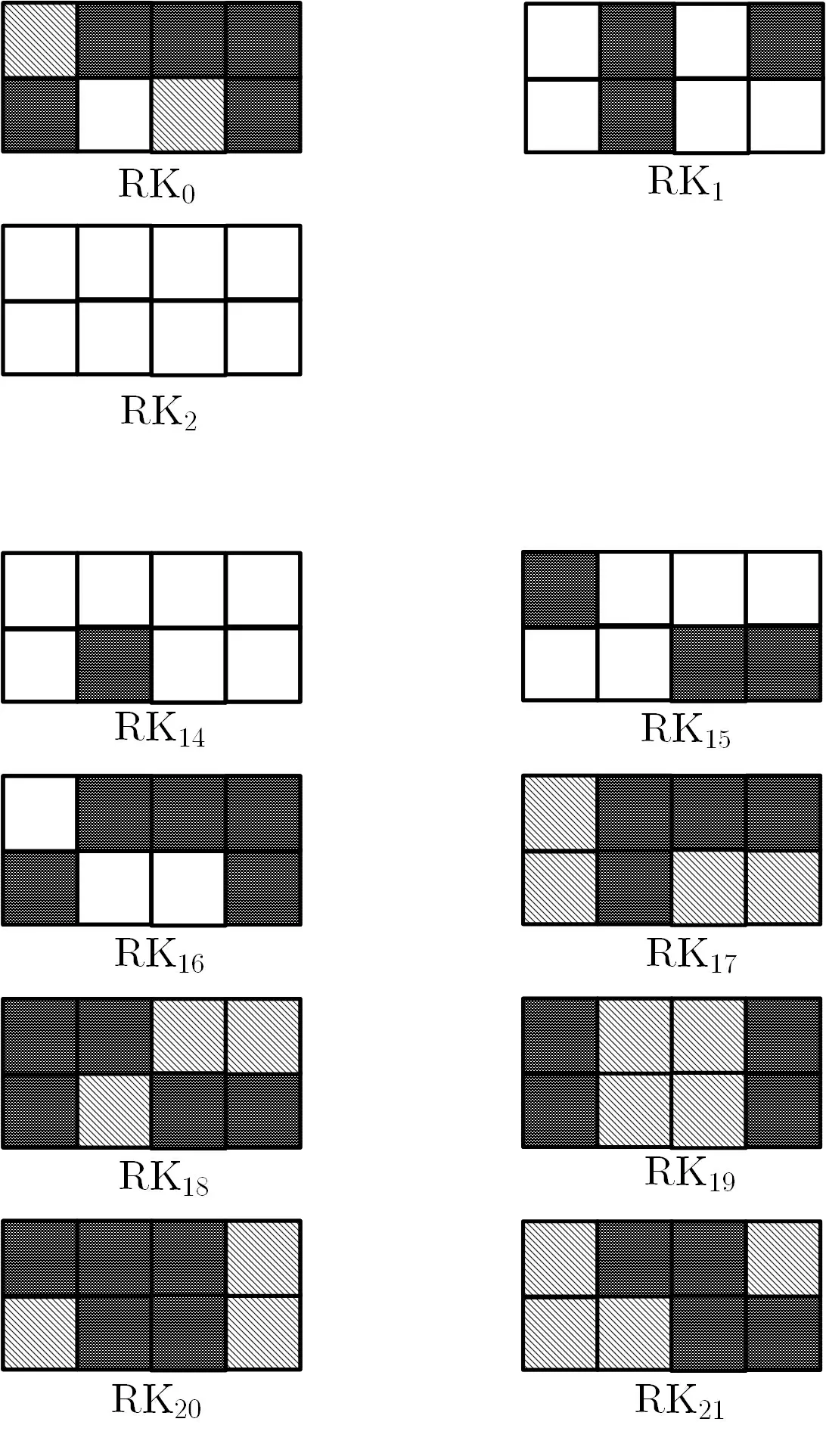
图8 密钥桥技术在攻击过程中的应用Figure 8 Application of key-bridge technique in MITM attack

3.3 攻击复杂度分析

上述22 轮的SKINNY-128-384 的攻击过程中, 包含离线攻击和在线攻击两个阶段. 离线攻击阶段需要猜测的字节数量为37 字节, 即生成的预存储表由2296个255 字节的多重集构成, 即离线存储复杂度约为2304字节. 在线攻击阶段, 选择明文量至多为296个明文, 即数据复杂度为296选择明文(CP). 在线攻击的计算量主要集中在步骤2 和步骤4, 以进行一次22 轮SKINNY-128-384 加密所需要的时间为单位,则在线攻击阶段的时间复杂度约为2376×28×(21+99)/(22×16)=2382.45次22 轮SKINNY-128-384 加密.

4 结论

本文在建立SKINNY 算法中间相遇区分器的过程中, 将部分状态值的猜测转化为了密钥的猜测, 再结合密钥桥技术, 找到了SKINNY-128-384 算法存储复杂度更低的10.5 轮中间相遇区分器, 并给出了22轮SKINNY-128-384 算法的中间相遇攻击过程. 然而, 利用本文的方法寻找SKINNY-128-384 算法的11轮区分器时, 能找到的最优区分器复杂度为48 字节, 与算法的密钥全空间大小一致, 并不能构成有效的中间相遇区分器, 因此能够找到的最长轮数区分器仍然为10.5 轮. 寻找轮数更长的区分器, 还需要结合其他相关技术. 在攻击的过程中, 如何进一步减少密钥的猜测量, 降低攻击的时间复杂度, 也是一个值得研究的问题.