Y形旋转超声波马达的设计与动态特性分析

张 锦，刘佩珊，殷玉枫

（1.太原科技大学机械工程学院，山西太原030024；2.山西交通职业技术学院工程机械系，山西太原030031）

不同于传统电磁马达，超声波马达因具有转矩大、响应迅速和不受电磁干扰等优点，在航空航天领域具有广阔的应用前景［1‐3］。自20世纪后叶至今，超声波马达发展迅速，各国科研机构研发了多种超声波马达新结构［4‐9］。其中，旋转超声波马达的结构灵活多变，其工作机理为：先通过激发压电材料的逆压电效应使弹性基体产生超声振动，再通过摩擦耦合进行能量转换，实现转子的旋转［10‐11］。

超声波马达弹性基体的结构和压电材料的布置情况与极化方式决定了其工作性能，结构紧凑、驱动原理设计巧妙的超声波马达可在减小损耗的同时提高响应速度和定位精度［12‐13］。例如：2013年，浙江大学的白洋提出了一种可同时作旋转运动和直线运动的超声波电机［14］；2014年，日本学者Mashimo设计了一种定子为带有通孔的金属立方体的超声波马达，其压电元件粘贴在金属立方体的各个侧表面，该马达的体积仅为 1 mm3［15］；2016 年，中国科学院的潘巧生针对现有压电马达的不足，采用不借助摩擦力的方式实现了压电马达在速度、功率等方面的优化，并首次提出了基于偏心轮受迫振动的压电马达［16］。旋转超声波马达是超声波马达的重要部分，在结构设计时应尽量实现微型化和集成化，扩大其在微电机系统中的应用范围［17‐18］。

基于此，笔者拟采用Y形弹性基体，设计一种Y形旋转超声波马达，其整体结构对称，3组压电陶瓷片粘贴于Y形弹性基体表面，工作时分别对3组压电陶瓷片施加不同的交变电压，在3组压电陶瓷片横向振动模态的叠加作用下，驱动足端面产生驱动转子旋转的驱动力。然后，通过有限元方法对Y形旋转超声波马达定子组件进行优化设计，并对其动态特性进行分析。

1 Y形旋转超声波马达的结构及材料选择

1.1 Y形旋转超声波马达的结构

Y形旋转超声波马达的结构如图1所示，其由定子组件（由Y形弹性基体以及粘贴于弹性基体表面的3组压电陶瓷片构成，粘贴材料为导电环氧胶）、转子、轴承以及底座组成。Y形弹性基体与转子接触的部分为驱动足端面，在转子外弧面以及驱动足端面处粘贴摩擦材料。为了防止摩擦面发生蠕动，选择动、静摩擦系数相近的尼龙作为摩擦材料。

图1 Y形旋转超声波马达的三维结构Fig.1 Three‐dimensional structure of Y‐shaped rotary ultra‐sonic motor

图2为Y形旋转超声波马达定子组件中压电陶瓷片的布置情况与极化方向。压电陶瓷片均沿厚度方向（图中箭头方向）极化，其中压电陶瓷片1，2的极化方向相反，压电陶瓷片3，4，5，6的极化方向一致。

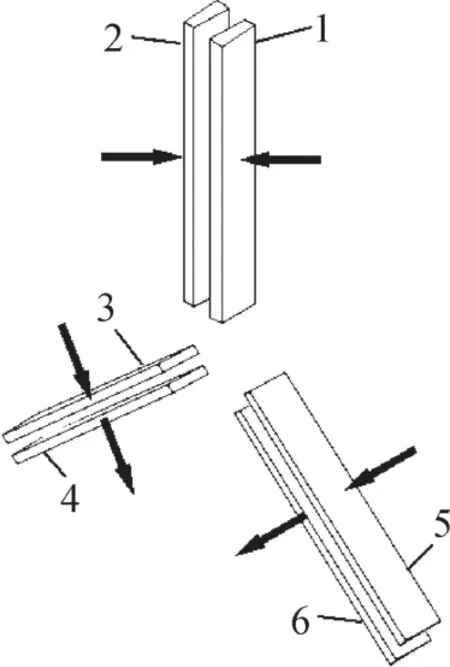
图2 压电陶瓷片的布置情况与极化方向Fig.2 Arrangement and polarization direction of piezoelec‐tric ceramic plate

1.2 Y形旋转超声波马达的材料选择

Y形旋转超声波马达定子组件的弹性基体采用具有较好加工工艺性能的45钢，其具有较大的刚度、良好的耐磨度和较高的弹性系数。45钢的性能参数如表1所示。

表1 45钢的性能参数Table 1 Performance parameters of 45 steel

选择合适的压电陶瓷材料能够使弹性基体的振幅达到最大，从而使超声波马达在最佳驱动频率下工作。压电陶瓷片在外加电压的激励下会产生横向振动模态和纵向振动模态。超声波马达需在3组压电陶瓷片横向振动模态的作用下工作，故选择压电常数较大的压电陶瓷片；同时，为了避免模态干扰，需尽量使纵向振动小一些。因此，选择PZT‐5H压电陶瓷片作为本文Y形旋转超声波马达的压电材料。

2 Y形旋转超声波马达的工作机理

对于Y形旋转超声波马达，其Y形弹性基体可被视作由3段均匀的弹性梁组成，每段梁上均粘有压电陶瓷片。当对压电陶瓷片施加交变电压时，其将产生横向振动模态，进而激发弹性梁受迫振动。设弹性梁的长度为L，压电陶瓷片的厚度为h。当施加在压电陶瓷片上的交变电压为V时，压电陶瓷片产生的横向振动位移为d(x，t)，则其平均电场强度E(x，t)和应变ε(x，t)分别为：

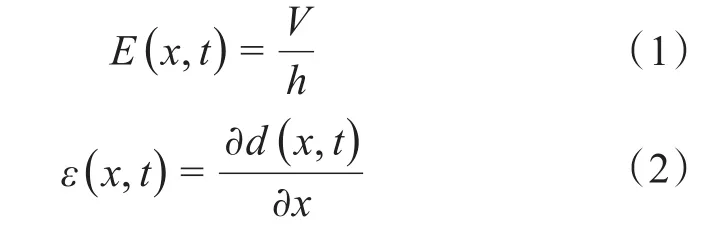
则弹性梁的应变εL为：

式中：SL——压电陶瓷片的横截面积。

由此可得在压电陶瓷片横向振动的激励下，弹性梁的振动方程为：

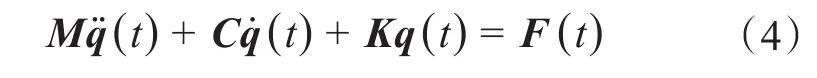
式中：M——弹性梁的质量矩阵；

C——弹性梁的阻尼矩阵；

K——弹性梁的刚度矩阵；

q̈(t)——弹性梁的加速度；

q̇(t)——弹性梁的速度；

q(t)——弹性梁的位移；

F(t)——弹性梁受到的合外力。

则弹性梁的受迫振动响应u(x，t)为［1］：

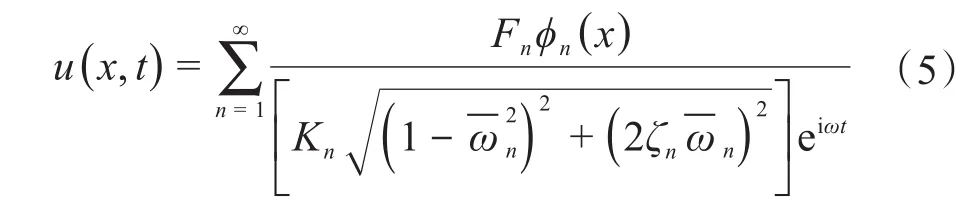
式中：Fn——弹性梁的第n阶模态力；

φn(x)——弹性梁的第n阶模态振型；

——弹性梁的第n阶模态刚度；

ζn——弹性梁的第n阶振幅；

ω——激振频率。

Y形旋转超声波马达弹性基体在受迫振动时，产生3种横向振动模态。在3种横向振动模态叠加作用下驱动足产生对转子的驱动力，从而实现转子旋转。在对压电陶瓷片施加交变电压时，定子组件驱动转子旋转的过程如图3所示。

图3 定子组件驱动转子旋转的过程Fig.3 Process of rotor rotation driven by stator assembly

根据图3，Y形旋转超声波马达工作时，其定子组件驱动转子旋转的过程分为以下2个步骤：

1）对压电陶瓷片1施加正向电压，压电陶瓷片1伸长，对压电陶瓷片2施加反向电压，压电陶瓷片2收缩，使得Y形弹性基体的上半部分产生图3（a）中虚线所示方向的形变，下半部分产生逆时针扭转位移。此时，左侧驱动足端面压紧转子，与转子外弧面形成摩擦耦合面；右侧驱动足端面偏离转子外弧面一定距离，不与转子产生接触面。对压电陶瓷3，4，5，6同时施加反向电压，Y形弹性基体下半部分的左、右侧同时收缩，左侧驱动足端面在与转子外弧面形成的摩擦耦合面的摩擦作用下产生对转子的驱动力，方向为沿右上方。

2）对压电陶瓷片1施加反向电压，压电陶瓷片1收缩；对压电陶瓷片2施加正向电压，压电陶瓷片2伸长，使得Y形弹性基体的上半部分产生图3（b）中虚线所示方向的形变，下半部分产生顺时针扭转位移。此时，右侧驱动足端面压紧转子，与转子外弧面形成摩擦耦合面；左侧驱动足端面偏离转子外弧面一定距离，不与转子产生接触面。对压电陶瓷3，4，5，6同时施加正向电压，Y形弹性基体下半部分的左、右侧同时伸长，右侧驱动足端面在与转子外弧面形成的摩擦耦合面的摩擦作用下产生对转子的驱动力，其方向为沿右下方。

当定子组件按图3连续运动时，转子顺时针旋转。分别交换步骤1）、2）中对压电陶瓷片1，2施加的电压的方向，可实现转子的逆时针旋转。

3 Y形旋转超声波马达定子组件优化设计

超声波马达定子组件的结构尺寸是影响其性能的重要因素，因此需要对定子组件进行优化设计。利用Workbench软件的Design Exporation模块对Y形旋转超声波马达定子组件的尺寸进行优化分析，该定子组件的尺寸参数如图4所示，其中：l1、c分别为Y形弹性基体上半部分的长度和厚度；l2、a分别为Y形弹性基体下半部分的长度和厚度。

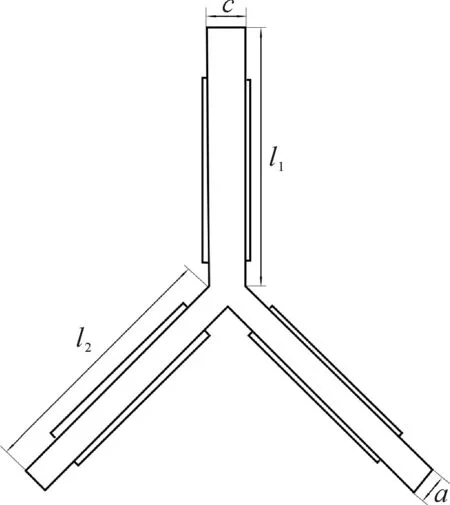
图4 定子组件尺寸参数Fig.4 Dimensional parameters of stator assembly

首先确定对Y形旋转超声波马达定子组件振动特性影响较大的尺寸参数，并以其作为设计依据。设置定子组件各尺寸参数的取值范围，如表2所示。

表2 定子组件各尺寸参数的取值范围Table 2 Value range of each dimension parameter of stator assembly

利用Response Surface优化设计模块浏览、更新设计点，并进行响应面分析，得到定子组件各尺寸参数的灵敏度柱状图，如图5所示。

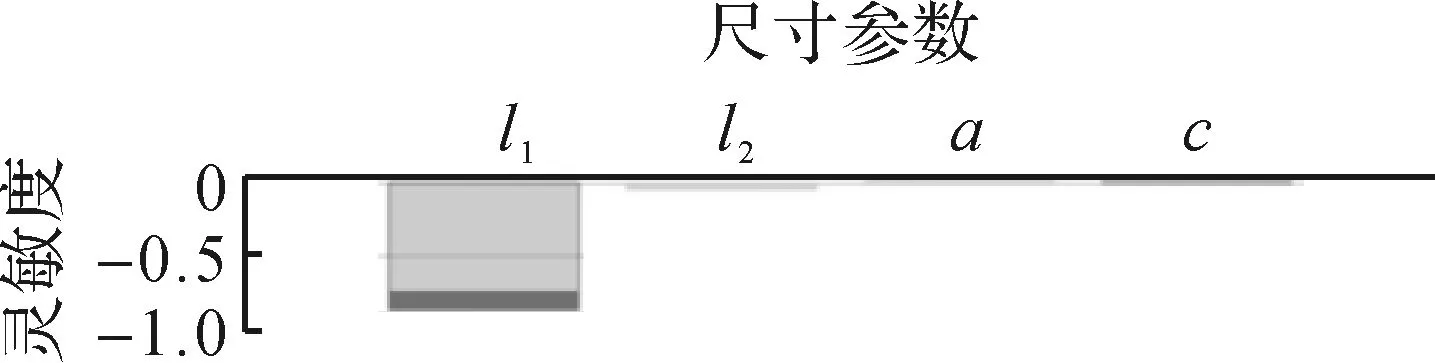
图5 定子组件各尺寸参数的灵敏度柱状图Fig.5 Sensitivity histogram of each dimension parameter of stator assembly

由图5可以看出，灵敏度最高的尺寸参数是l1，因此在对定子组件进行优化设计时，应优先确定l1。

建立尺寸参数l1、l2与定子组件变形量的响应面，如图6所示。从图6中可以看出，当l1=18 mm时，定子组件的变形量最大，故选择l1=18 mm。当l1=18 mm时，定子组件的变形量与l2成正比，因此取l2=10 mm。

图6 l1、l2与定子组件变形量的响应面Fig.6 Response surface of l1,l2and stator assembly deformation

鉴于定子组件尺寸参数a、c的灵敏度较低，考虑到加工精度要求，取a=c=3 mm。

4 优化后Y形旋转超声波马达定子组件仿真分析

4.1 模态分析

在不施加外载荷的情况下，对结构进行模态分析可以得到结构在不同频率下的固有振型。Y形旋转超声波马达定子组件驱动力的形成取决于弹性基体横向振动模态的激发。对优化后的定子组件进行模态分析，以找到激发定子组件中弹性基体横向振动模态的固有频率。

首先，建立定子组件的有限元模型，如图7所示，整个模型含有465个单元和3 922个节点。然后，利用Block lancos法对优化后的定子组件进行模态分析，得到不同频率下定子组件的变形量。

图8所示为定子组件的前4阶模态振型。由图8可以看出，二阶模态为Y形旋转超声波马达工作所需的振动模态。

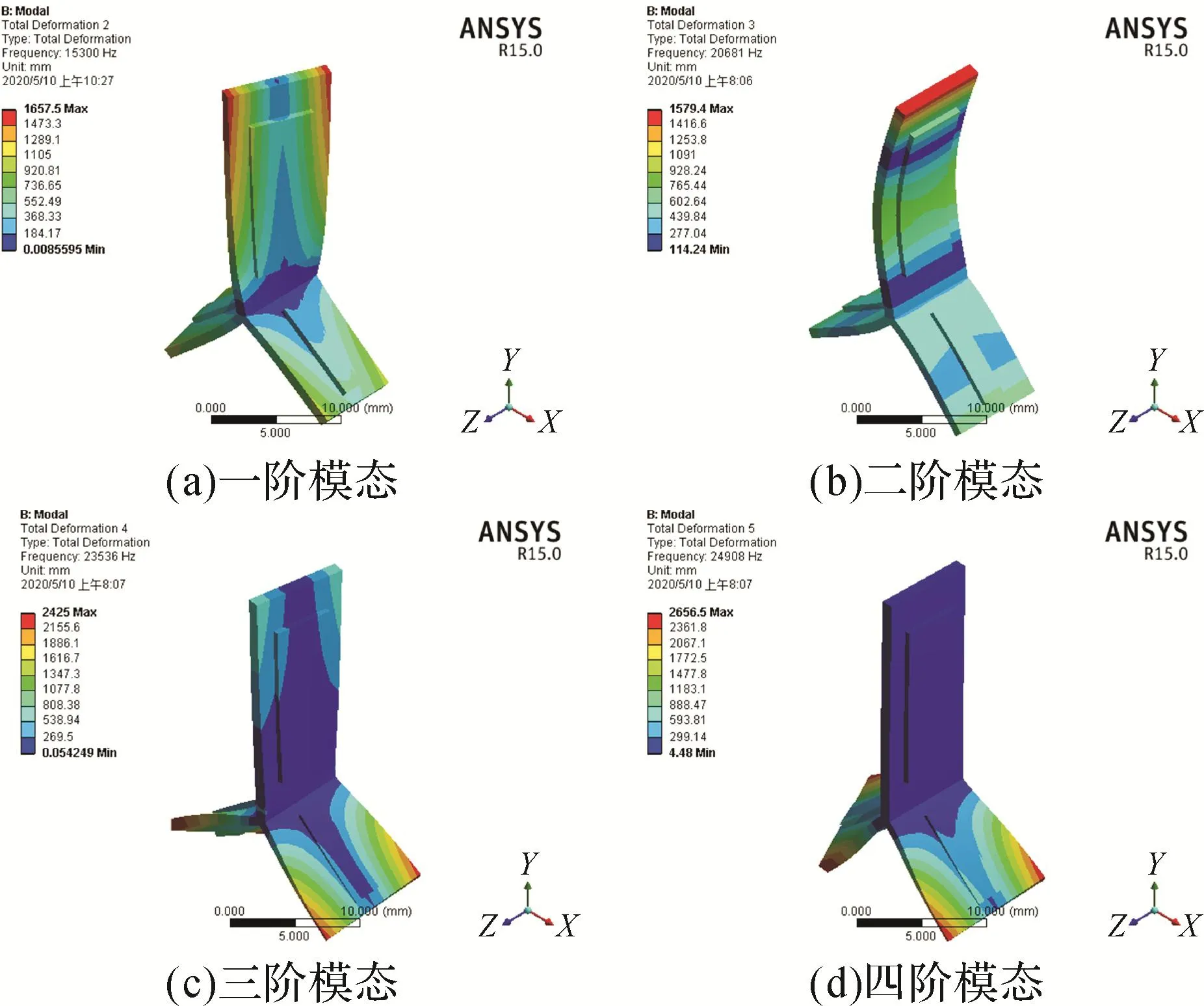
图8 定子组件前4阶模态振型Fig.8 Vibration shape of the first four modes of stator assembly

4.2 谐响应分析

通过谐响应分析可以确定Y形旋转超声波马达定子组件在不同频率电压激励下的响应量。在对定子组件进行谐响应分析时选择模态叠加法，即将通过模态分析得到的各个模态振型与其对应的系数相乘后叠加，该方法的计算速度较快。在3组压电陶瓷片的上、下表面上施加幅值为20 V的交变电压，设置频率为0～30 000 Hz，通过谐响应分析得到定子组件的幅频特性曲线，如图9所示。由图9可以看到，Y形旋转超声波马达定子组件驱动足端面的振幅在频率为20 000 Hz附近取得峰值。

图9 定子组件的幅频特性曲线Fig.9 Amplitude frequency characteristic curve of stator as‐sembly

设置频率为18 000～22 000 Hz，通过谐响应分析得到定子组件的局部幅频特性曲线，如图10所示。由图10可以看出，当频率为20 739 Hz时，Y形旋转超声波马达定子组件驱动足端面的振幅最大，为6.95μm。

图10 定子组件的局部幅频特性曲线Fig.10 Local amplitude frequency characteristic curve of sta‐tor assembly

4.3 瞬态分析

为了验证Y形旋转超声波马达定子组件的振动模态能否达到预期，对定子组件进行瞬态分析。在3组压电陶瓷片的上、下表面上施加幅值为10 V的交变电压作为激励，设置频率为20 739 Hz，通过瞬态分析得到定子组件在1个激励周期内的振动模态，如图11所示，图中箭头表示1个激励周期内定子组件的运动方向。定子组件的瞬态分析结果验证了Y形旋转超声波马达的驱动机理。

图11 1个激励周期内定子组件的振动模态Fig.11 Vibration mode of stator assembly in one excitation cycle

5 结论

1）设计了一种Y形旋转超声波马达，通过将3组沿厚度方向极化的压电陶瓷片粘贴在Y形弹性基体表面上，分别对3组压电陶瓷片施加交变电压，使其产生横向振动模态，在3个横向振动模态的叠加作用下激发驱动足端面产生驱动力，进而通过摩擦耦合驱动转子旋转。

2）利用响应面法对Y形旋转超声波马达定子组件的尺寸参数进行优化设计。结果表明：选择l1=18 mm，l2=10 mm，a=c=3 mm，可以在便于加工和保证结构稳定性的前提下，提升定子组件的性能。

3）建立优化后Y形旋转超声波马达定子组件的有限元模型，以幅值为10 V的交变电压作为激励，通过模态分析确定了Y形旋转超声波马达工作所需的振动模态；通过谐响应分析得到压电陶瓷片表面施加电压的最佳频率为20 729 Hz，该频率下驱动足端面的振幅最大，为6.95μm；通过瞬态分析得到了1个激励周期内定子组件的振动模态，验证了Y形旋转超声波马达的驱动机理。

Y形驱动超声波马达定子组件的结构简单，同时具有良好的对称性，2个驱动足端面的驱动有效提高了驱动效率；同时，模态叠加后定子组件的振幅较大，能效利用率高。本文设计实现了超声波马达的结构化创新，为拓宽超声波马达的应用领域提供了参考。