基于GSSEC的开关磁阻电机驱动的海洋绞车主动升沉补偿控制方法

严 颖，张小平，姜海鹏，张 铸，赵延明，黄良沛

（1.湖南科技大学海洋矿产资源探采装备与安全技术国家地方联合工程实验室，湖南湘潭411201；2.湖南科技大学信息与电气工程学院，湖南湘潭411201；3.湖南科技大学先进矿山装备教育部工程研究中心，湖南湘潭411201）

海洋绞车是应用于海洋科学考察与海洋资源勘探及开发的重要收放设备［1‐2］。为了克服海上风浪流等强非线性干扰对海洋绞车正常作业的影响，一般要求海洋绞车具有主动升沉补偿功能［3‐4］。但是，作为目前海洋绞车主动升沉补偿动力驱动发展方向的交流变频电机驱动虽具有结构简单、性能可靠和调节方便等优点［5］，但驱动用交流变频电机存在起动电流大、过载能力低及功率因数不高等不足。对于海洋绞车主动升沉补偿要求频繁起制动、加减速以及往复运转的运行工况而言，交流变频电机驱动的总体运行效率不高及能耗大，且在实际应用中发热严重，直接影响了海洋绞车主动升沉补偿功能的持续使用，因此研究更有效的动力驱动方式变得十分迫切。

开关磁阻电机（switched reluctance motor，SRM）是20世纪80年代初随着交流调速技术的发展而开发出的一种新型电机［6‐7］，其具有很多优点［8‐10］，如起动电流小，起动转矩大，结构简单、坚固，效率高，容错能力强和调速范围宽等，因而非常适合用于海洋绞车主动升沉补偿控制系统。尤其是对于海洋绞车主动升沉补偿要求频繁起制动、加减速以及往复运转的运行工况而言，开关磁阻电机具有交流变频电机无法比拟的效率优势。因此，将开关磁阻电机应用于海洋绞车主动升沉补偿控制系统具有重要意义。

若要实现海洋绞车主动升沉补偿的高精度、恒张力控制，则必须通过控制其驱动电机来实现海洋绞车转筒的运转与母船升沉运动保持同步，此时驱动电机须频繁正反转且转速实时变化。一旦驱动电机的实际转速不能准确跟踪其时变给定转速，就无法满足海洋绞车主动升沉补偿的同步控制要求。因此，针对开关磁阻电机研究有效的控制策略是实现海洋绞车主动升沉补偿同步控制的关键。

目前，国内外学者已针对开关磁阻电机调速控制展开了一系列研究，并提出了多种有效的控制方法［11‐13］。但是，对于时变给定转速跟踪控制的研究却不多见，现主要有基于超扭矩算法的二阶滑模控制（second order sliding mode control，SOSMC）［14］和自校正 TSK 模糊控制（adaptive Takagi‐Sugeno‐Kang fuzzycontrol，ATSKFC）［15］2种控制方法。其中，SOSMC方法对控制系统参数变化和外部扰动有较好的鲁棒性，但其转速跟踪精度不高；ATSKFC方法虽具有较高的转速跟踪精度，但存在转速过零时稳定性差的问题。对于海洋绞车主动升沉补偿控制来说，上述2种控制方法均难以满足其同步控制要求。为此，针对开关磁阻电机驱动的海洋绞车主动升沉补偿控制系统，笔者提出了一种基于渐进稳态控制信号误差控制（gradual steady state control signal‐error control，GSSEC）的开关磁阻电机调速控制方法［16］，并对该控制方法的基本原理、具体设计方法及其控制参数的优化方法进行分析，最后通过仿真分析和试验对该控制方法的效果进行验证。

1 开关磁阻电机数学模型

根据文献［17］，开关磁阻电机的电压平衡方程为：

式中：U、I、ψ（θ，I）和R分别为开关磁阻电机定子绕组的外加电压、电流、磁链和电阻；θ为开关磁阻电机转子的位置角。

开关磁阻电机的瞬时电磁转矩方程为：

其中：

式中：Te为开关磁阻电机的瞬时电磁转矩；W′( )θ，I 为磁共能；C为常数。

开关磁阻电机的机械运动方程为：

式中：J、D和TL分别为开关磁阻电机的转动惯量、摩擦系数和负载转矩。

式（1）至式（3）构成了开关磁阻电机的数学模型。

2 基于GSSEC的开关磁阻电机调速控制方法

根据海洋绞车主动升沉补偿的同步控制要求，针对开关磁阻电机调速系统，提出了一种基于GSSEC的调速控制方法。基于GSSEC的开关磁阻电机调速控制系统框图如图1所示，其包括转速外环和转矩内环，其中转速外环采用GSSEC算法，转矩内环采用直接转矩控制方法。

图1 基于GSSEC的开关磁阻电机调速控制系统框图Fig.1 Block diagram of SRM speed control system based on GSSEC

2.1 基本原理

GSSEC算法是一种不依赖于被控对象精确数学模型的控制方法。基于GSSEC的开关磁阻电机调速控制系统转速外环的基本原理如图2所示［16］，主要包括非线性误差控制算法和采样保持两部分，其中非线性误差控制算法用于对当前采样时刻开关磁阻电机的给定转速与实际转速的偏差Δn（k）进行处理，得到相应的控制输出u1（k）；采样保持部分则用于采集并保持上一采样时刻开关磁阻电机调速控制系统的总输出Te*（k-1），并利用Te*（k-1）对u1（k）进行补偿，得到当前采样时刻开关磁阻电机调速控制系统的总输出Te*（k），其也为转矩内环的参考转矩。图2中限幅环节用于限制总输出的幅值。

图2 基于GSSEC的开关磁阻电机调速控制系统转速外环的基本原理Fig.2 Basic principle of speed outer loop of SRM speed con‐trol system based on GSSEC

2.2 具体设计

GSSEC算法的离散表达式为：

式中：Δn（k-1）为上一采样时刻的转速偏差；KT为控制参数，KT>0；vs（k）为当前采样时刻控制系统输出误差的标准变化率。

根据GSSEC算法的基本原理，可将vs（k）设计为：

式中：K1p、K2p（p=1，2，…，4）为GSSEC算法的控制参数，且满足K2p>K1p>0。

2.3 控制参数优化

基于GSSEC的开关磁阻电机调速控制方法的控制效果与GSSEC算法的控制参数KT、K1p和K2p（p=1，2，…，4）密切相关。鉴于果蝇优化算法（fruit fly opti‐mization algorithm，FOA）具有寻优精度高、收敛快和算法简单等特点［18‐19］，采用该算法对上述控制参数进行优化。

以控制参数KT、K1p和K2p（p=1，2，…，4）为优化对象，以开关磁阻电机的实际转速与给定转速的偏差Δn（t）最小为优化目标，利用Δn（t）的时间误差绝对积分（integrated time absolute error，ITAE）［20］构建目标函数，并将其值作为味道浓度S，即：

采用FOA对GSSEC算法的控制参数进行优化，具体流程如图3所示。

图3 基于FOA的GSSEC算法控制参数优化流程Fig.3 Optimization flow of control parameters of GSSEC al‐gorithm based on FOA

由图3可知，基于FOA的GSSEC算法控制参数的优化主要包括以下9个步骤。

步骤1 初始化种群规模N、最大迭代次数nmax和初始果蝇群体的位置（X′，Y′）。

步骤2 配置控制参数KT和K2p的果蝇个体的随机搜索方向和距离，获得其果蝇个体的位置。其中，控制参数K2p的第j个果蝇个体的位置可表示为：

式中：XK2p(j)、YK2p(j)分别为控制参数K2p的第j个果蝇个体所在位置的横、纵坐标；rand（）为随机值。

步骤3 根据步骤2中K2p的果蝇个体位置以及K1p和K2p所满足的条件（K2p>K1p>0），设置控制参数K1p的第j个果蝇个体的位置，即：

式中：XK1p(j)、YK1p(j)分别为K1p的第j个果蝇个体所在位置的横、纵坐标；a为大于0的系数。

步骤4 获取第l个控制参数的第j个果蝇个体对应的味道浓度判定值Sl（j）（l=1，2，…，9），为：

式中：Xl(j)、Yl(j)分别为第l个控制参数的第j个果蝇个体所在位置的横、纵坐标。

步骤5 根据计算得到的味道浓度判定值获得对应的转速偏差Δn（t）。

步骤6 将获得的转速偏差Δn（t）代入式（6），计算得到第j个果蝇个体的味道浓度S（j）。

步骤7 判断j是否到达果蝇群体数量的上限，若到达果蝇群体数量的上限，则执行步骤8；否则执行步骤2。

步骤8 在果蝇群体中找出味道浓度最小的果蝇个体作为最优个体，并保留最优果蝇个体的味道浓度和位置。

步骤9 判断是否到达最大迭代次数nmax，若已到达，则输出最优果蝇个体的味道浓度判定值，即控制参数KT、K1p和K2p的最优解；否则，迭代次数加1后，返回步骤2。

3 仿真分析

采用MATLAB软件对基于GSSEC的开关磁阻电机调速控制方法的效果进行仿真验证。同时，为便于与文献［15］提出的ATSKFC方法进行对比分析，参照文献［15］设置相关参数：采用四相8/6极开关磁阻电机，其功率P=3 kW，定子绕组的电阻R=130 mΩ，转动惯量J=0.001 7 kg⋅m2，摩擦系数D=0.001 N⋅m⋅s；负载转矩TL=2 N⋅m，给定磁链ψ=0.3 Wb。根据图3所示的GSSEC算法控制参数优化流程，得到1组最优控制参数：KT=6.592 37，K11=1.294 39，K12=2.43640，K13=5.78634，K14=4.01125，K21=3.17456，K22=3.822 70，K23=10.091 11和K24=7.148 87。为了便于验证基于GSSEC的开关磁阻电机调速控制方法的效果，分别针对给定转速时变和负载突变两种情况进行仿真分析。

3.1 转速跟踪控制仿真分析

考虑到母船升沉运动的运动方程可近似为正弦函数［1］，在验证转速跟踪效果时，用正弦函数形式来表示开关磁阻电机的给定转速。根据文献［15］，设开关磁阻电机的给定转速为1 200sin t r/min。通过仿真分析得到开关磁阻电机的实际转速及转速跟踪偏差，如图4所示。

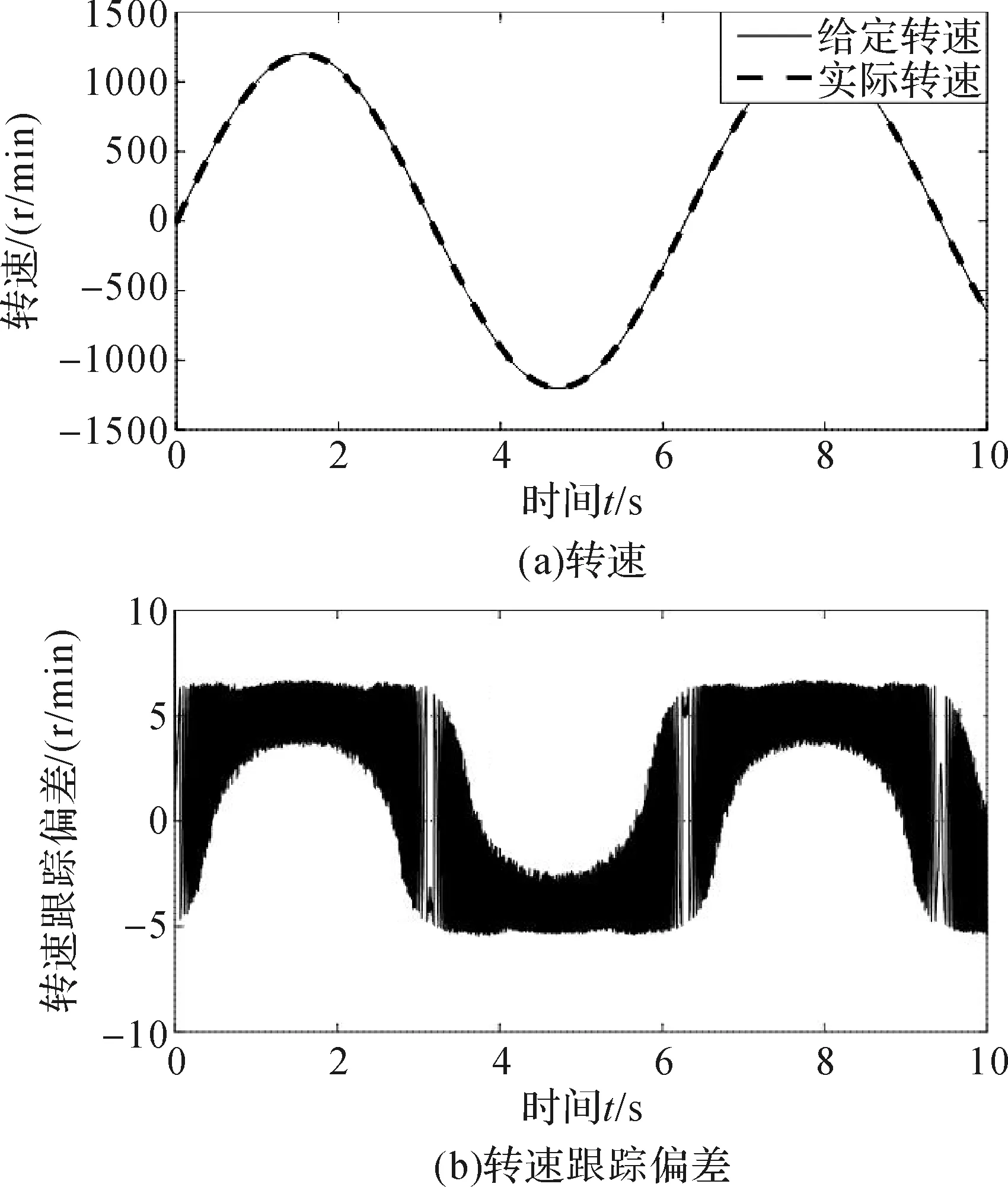
图4 给定转速为1 200sin t r/min时开关磁阻电机的实际转速及转速跟踪偏差Fig.4 Actual speed and speed tracking deviation of SRM with given speed of 1 200sin t r/min

为了便于说明基于GSSEC的开关磁阻电机调速控制方法的转速跟踪效果，采用转速跟踪相对误差δ作为评价转速跟踪效果的性能指标，其计算式为：

式中：Δn1为开关磁阻电机转速跟踪偏差的均方根；为开关磁阻电机给定转速的最大值。

根据图4结果，利用式（10）计算得到给定转速为1 200sin t r/min时开关磁阻电机的转速跟踪相对误差δ=0.347 0%。由此可见，基于GSSEC的调速控制方法实现了开关磁阻电机对时变给定转速的准确跟踪。

为验证基于GSSEC的开关磁阻电机调速控制方法在不同给定转速下的转速跟踪效果，通过改变给定转速进行分析。设给定转速分别为1 200sin 1.5t和1 500sin tr/min，通过仿真分析得到不同给定转速下开关磁阻电机的实际转速及转速跟踪偏差，分别如图5和图6所示。不同给定转速下开关磁阻电机的转速跟踪相对误差如表1所示。由表1可知，在不同给定转速下，基于GSSEC的调速控制方法均可实现开关磁阻电机对给定转速的准确跟踪。

表1 不同给定转速下开关磁阻电机的转速跟踪相对误差仿真结果Table 1 Simulation results of relative error of speed tracking of SRM under different given speeds

图5 给定转速为1 200sin 1.5t r/min时开关磁阻电机的实际转速及转速跟踪偏差Fig.5 Actual speed and speed tracking deviation of SRM with given speed of 1 200sin 1.5t r/min

图6 给定转速为1 500sin t r/min时开关磁阻电机的实际转速及转速跟踪偏差Fig.6 Actual speed and speed tracking deviation of SRM with given speed of 1 500sin t r/min

3.2 负载突变控制仿真分析

为验证基于GSSEC的开关磁阻电机调速控制系统的带负载能力，设开关磁阻电机的给定转速为1 000 r/min，初始负载转矩为2 N⋅m，在t=2 s时突加1 N⋅m负载，在t=7 s时再突卸1 N⋅m负载。通过仿真分析得到开关磁阻电机的实际转速和电磁转矩，分别如图7和图8所示。从图7和图8中可以看出，当负载发生突变时，开关磁阻电机的转速基本无变化，其电磁转矩可根据负载变化情况迅速达到新的稳态，说明基于GSSEC的开关磁阻电机调速控制系统具有良好的带负载能力。

图7 突加负载时开关磁阻电机的实际转速及电磁转矩Fig.7 Actual speed and electromagnetic torque of SRM un‐der suddenly loading

图8 突卸负载时开关磁阻电机的实际转速及电磁转矩Fig.8 Actual speed and electromagnetic torque of SRM un‐der suddenly unloading

4 试验验证

为进一步验证基于GSSEC的开关磁阻电机调速控制方法的效果，以TMS320F28335 DSP控制器为控制核心，搭建了基于GSSEC的开关磁阻电机调速控制系统试验平台，如图9所示。该试验平台包括1台3 kW的四相8/6开关磁阻电机、控制器、光电编码器、卷扬机、示波器及1台PC（personal computer，个人计算机）等。其中开关磁阻电机与卷扬机相连，通过卷扬机卷筒上的缆绳带动负载。为与仿真分析结果进行对比，试验中相关参数的设置与仿真分析时一致。另外，为了验证本文控制方法的转速跟踪精度，与现有控制方法中精度较高的ATSKFC方法进行对比分析。

图9 基于GSSEC的开关磁阻电机调速控制系统试验平台Fig.9 Experimental platform of SRM speed control system based on GSSEC

4.1 转速跟踪控制试验

根据仿真分析中设置的3种给定转速，开展转速跟踪控制试验，得到开关磁阻电机实际转速的波形如图10所示。由图10可知，不同给定转速下开关磁阻电机实际转速的波形与仿真结果相吻合。根据图10结果，计算不同给定转速下开关磁阻电机的转速跟踪相对误差δ，如表2所示。对比表1和表2可知，试验结果和仿真结果基本吻合，且转速跟踪相对误差的变化均很小，这进一步验证了基于GSSEC的开关磁阻电机调速控制方法具有良好的转速跟踪性能。

表2 不同给定转速下开关磁阻电机的转速跟踪相对误差试验结果Table 2 Experimental results of relative error of speed tracking of SRM under different given speeds

图10 不同给定转速下开关磁阻电机实际转速的波形Fig.10 Waveform of actual speed of SRM under different given speeds

4.2 负载突变控制试验

与仿真分析一致，开展基于GSSEC的开关磁阻电机调速控制系统的负载突变控制试验时，设开关磁阻电机的给定转速为1 000 r/min，初始负载转矩为2 N⋅m，在t=2s时突加1N⋅m负载，在t=7s时突卸1N⋅m负载，得到的开关磁阻电机实际转速的波形如图11所示。由图11可知，当负载发生突变后，开关磁阻电机的转速基本无变化，说明基于GSSEC的开关磁阻电机调速控制系统具有较强的带负载能力。

图11 负载突变时开关磁阻电机实际转速的波形Fig.11 Waveform of actual speed of SRM under sudden load change

4.3 不同控制方法的性能对比

根据文献［15］，在相同试验条件下，对比本文提出的基于GSSEC的控制方法和ATSKFC方法的转速跟踪相对误差。通过试验得到，当给定转速为1 200sintr/min时，2种控制方法下开关磁阻电机的转速跟踪相对误差δ如表3所示。相比于ATSKFC方法，采用基于GSSEC的控制方法时开关磁阻电机的转速跟踪相对误差δ减小了21.33%。由此可知，采用基于GSSEC的控制方法时开关磁阻电机对转速的跟踪精度更高。

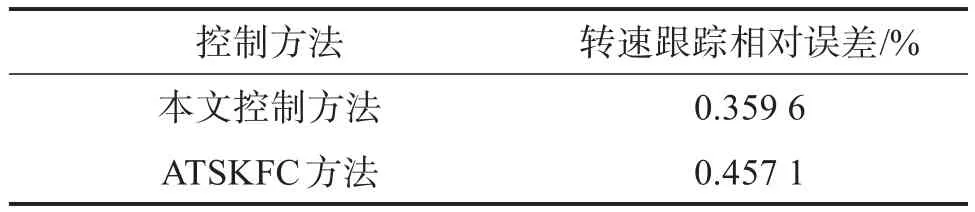
表3 给定转速为1 200sin t r/min时不同控制方法下开关磁阻电机的转速跟踪相对误差对比Table 3 Comparison of relative error of speed tracking of SRM under different control methods with given speed of 1 200sin t r/min

5 结论

针对开关磁阻电机驱动的海洋绞车主动升沉补偿控制系统，提出了一种基于GSSEC的调速控制方法。通过建立开关磁阻电机的数学模型，并结合海洋绞车主动升沉补偿的同步控制要求，对基于GSSEC的开关磁阻电机调速控制方法的基本原理、具体设计方法及其控制参数的优化方法进行了分析，并通过仿真分析和试验对其效果进行了验证，同时还与ATSKFC方法进行了对比分析。结果表明：基于GSSEC的控制方法具有转速跟踪精度高和带负载能力强等特点，可为实现开关磁阻电机应用于海洋绞车主动升沉补偿控制系统奠定理论基础。