矿渣-水泥水化动力模型研究

唐 剑， 楼伟杰， 付海华， 王家栩， 谌联平

(南昌理工学院，江西 南昌 330013)

混凝土是目前使用范围最广泛的一种建筑材料，其强度、耐久性与其中水泥水化过程有很大的关系。矿渣等工业废料既可以节省水泥用量，又可以改善混凝土的内部结构，提高混凝土力学耐久性能[1]。

水泥的主要成分有石膏、C3A、C4AF、C2S和C3S，水泥水化是一个复杂的化学反应过程，而矿渣等火山灰材料在氢氧化钙的激发下会改变水泥的水化过程。而现有水化动力学模型通常把矿渣-水泥看作一个整体，把复合胶凝材料当作均质材料去研究其动力学过程和动力学参数[2]，这并不能够清晰准确地反映矿渣的反应机理及表征矿渣-水泥的水化动力学[3-4]。

因此，对于矿渣-水泥体系的水化过程，由于实验对象和手段、研究目标与侧重点的差异，得到的结论也有较大差别，因此有必要对矿渣-水泥水化动力学模型进行研究，这也助于水泥水化程度的预测，进而评估水泥基材料的性能。

1 纯硅酸盐水泥水化动力学模型

C3S的水化动力模型目前研究得比较多，也具有一定的代表性。虽然C3A、C4AF、C2S对水泥水化热的影响较小，但对水泥浆中水化产物的影响仍然比较明显。因此，本文在纯C3S水化动力学模型的基础上，提出纯硅酸盐水泥的水化动力学模型。

C3S水化过程反应方程如式(1)。

(1)

与纯C3S不同，纯硅酸盐水泥水化的晶核生长速率、成核速率是恒定不变的，因此在局部生长假说的基础上，引入了CSH的法向长度。假设到t时刻水泥水化的晶核生长的法向长度，考虑距C3S表面高度为y的平面与该晶核相交圆，该圆面积为式(2)。

Acircle(x,t,y)=πg[G2(t-x)2-y2]

(2)

则x时刻产生的所有晶核在t时刻与y截面相交圆的总截面积离散化为式(3)。

(3)

临界长度范围内CSH的体积分数计算见式(4)。

Vextended(t)=

(4)

CSH在其空间内的体积分数计算见式(5)(Vwater为体系内可供水化产物生长的空间)。

VCSH(t)=Vwater×Vextended(t)

(5)

CSH凝胶沉淀速率计算见式(6)。

(6)

则水泥的反应速率计算见式(7)。

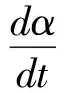
(7)

动力学方程为式(8)。

α[i]=α[i-1]+

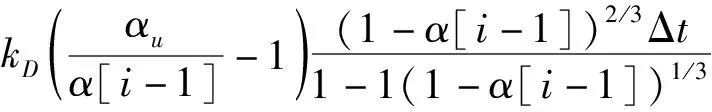
(8)

2 矿渣-水泥复合材料水化动力学模型推导

矿渣在水泥中的化学作用主要是指其火山灰反应，即，硅酸盐水泥水化产物为矿渣提供了稳定的碱性环境，激发了矿渣自身的水化反应活性。本文在选取矿渣主要化学组成和矿渣主要反应产物的化学组成为相应的动力学的基础上推导矿渣水化动力学模型。

2.1 基本参数的确定

矿渣的化学组成如表1所示，选定矿渣反应产物的化学组成如表2所示。

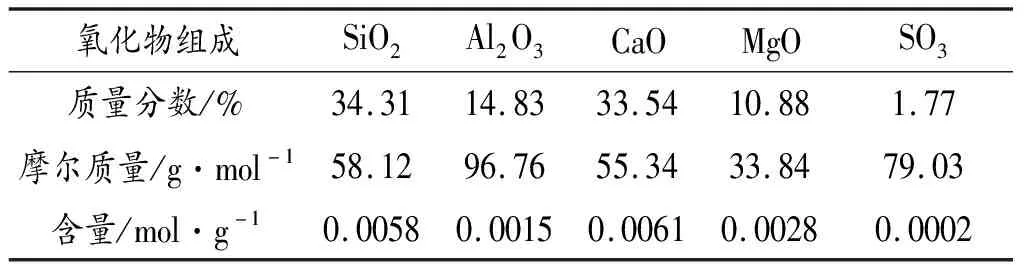
表1 矿渣主要化学组成及其含量

表2 矿渣主要反应产物的化学组成

矿渣的反应方程式见式(9)。

100·矿渣+15.76g·CH+

40.72g·C4AH13+30.86g·M4AH10+

10.21g·C6AS3H32+2.95g·U

(9)

式中，U为矿渣中不参与反应的物质统一标记。

2.2 矿渣-水泥复合材料水化动力学模型

Atrul,SCM(t,y)为t时刻矿渣反应产物的固定晶核与y高度界面相交圆的总面积，计算公式见式(10)。

(10)

Vextended,SCM(t)为临界长度范围内矿渣反应产物的体积分数，计算公式见式(11)。

(11)

VPSCM(t)为矿渣反应产物生长的空间范围内的反应产物总体积，计算公式见式(12)。

VPSCM(t)=(Vwater-VCSH(t1))×Vextended,SCM(t)

(12)

由此可得矿渣反应程度，见式(13)。

(13)

动力学方程见式(14)。

αSCM[i]=αSCM[i-1]+

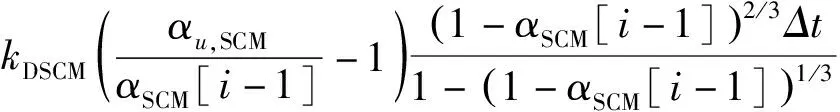
(14)

3 结论

建立水化动力学模型是研究水泥水化机理的重要方法。而水泥的水化提供了碱性环境，激发了矿渣的火山灰反应，因此，建立基于矿渣反应机理的矿渣-水泥水化动力学模型是非常有必要的。

本文以矿渣-水泥为研究对象，对纯硅酸盐水泥的水化动力学模型进行了修正，在此基础上建立了矿渣水泥体系水化动力学模型，其主要结论如下：

1)修正了纯硅酸盐水泥体系水化动力学模型。纯硅酸盐水泥水化的扩散控制阶段采用了修正的Jander方程，而且根据水泥水化的反应程度采用了不同的扩散系数。

2)建立了矿渣-水泥的水化动力学模型。首先确定了矿渣的反应方程式；矿渣-水泥水化的扩散控制阶段也采用了修正的Jander方程，而且综合考虑了矿渣反应程度和矿渣极限反应程度采用了不同的扩散系数。