基于不同计算方法的综合管廊结构特性对比研究

刘 伟 明， 何 江 达

(1.绵阳市水利规划设计研究院，四川 绵阳 621000；2.四川大学水利水电学院，四川 成都 610065)

1 概 述

地下综合管廊的建设可以提高城市地下空间利用率，保障城市绿色可持续发展，是解决城市化进程中若干市政建设通病的科学方式。2014年初，在国家一系列政策的引导下，全国大中城市地下综合管廊行业发展迅猛，从25个试点城市的初步探索开始，目前国内已有460多个城市地下综合管廊项目开始建设，全国正迎来城市地下综合管廊建设的新时代。

城市地下综合管廊通常为矩形闭合框架断面，分单仓、双仓或多仓结构，施工一般为明挖暗埋结合现浇法或装配法，其荷载作用机理以及衬砌结构特性与矿山法及盾构法施工的山岭和城市隧道有较大区别。目前国内外通常荷载-结构法开展综合管廊的结构特性计算分析，随着数值计算的逐渐普及应用，近年来不少学者与工程师开始采用地层-结构法开展综合管廊衬砌结构特性分析。赵尚毅等[1]对地下隧道衬砌结构内力计算的荷载结构法和地层结构法进行比较，认为荷载结构法尚不能充分考虑结构与围岩的共同作用，并提出了一种能考虑共同作用的荷载结构简化模型。宋玉香等[2]从复合式衬砌角度出发，以荷载作用于地层边界的模型对复合式衬砌的初支及二衬进行计算，并与荷载-结构法计算结果进行对比。徐文腾等[3]基于ANSYS软件采用地层结构法，考虑荷载分配系数，分析深埋隧道衬砌结构的位移、弯矩、轴力、剪力等力学特征参数。于晓[4]采用ABAQUS软件对多舱矩形综合管廊结构受力性能进行数值模拟分析，分析其受力性能和破坏特征，并对综合管廊的截面布局进行研究。黄涌泉[5]利用MIDAS-GEN有限元软件,计算管廊三种结构断面分别在多遇地震和罕遇地震作用下其内力分布特点以及变形规律。总体而言，目前尚缺乏荷载-结构法与地层-结构法对于管廊衬砌结构特性的对比研究，在一定程度上制约了地层-结构法的推广普及。

笔者使用Midas GTS NX软件，分别采用荷载-结构模型与地层-结构模型，对比研究不同埋深条件明挖暗埋双仓矩形管廊结构特性变化规律，分析两种方法对荷载、结构分配及结构响应的对应关系，为设计人员深入理解地层-结构法开展计算研究提供参考与借鉴。

2 方法与模型对比

2.1 工程问题

某双仓矩形管廊总宽15 m，高5 m(图1)，侧墙、顶板、底板及中隔墙均采用厚度为0.6 m的C30混凝土浇筑，地层为中风化泥岩，回填土石总高度至建基面50 m。回填土石分每5 m一级填筑(第一级与管廊顶齐平)。相关岩土体参数见表1、2，其中回填土石在荷载-结构法中采用直接按其容重考虑为外荷载作用于衬砌，地层-结构法中则按双曲线E-B模型考虑回填土石与地基及衬砌的相互作用与效应。

2.2 荷载-结构模型

荷载-结构法认为地层对地下建筑结构的作用只是产生在结构上的荷载，包括主动地层压力(土压力等)和被动地层压力(弹性抗力等)，衬砌在荷载的作用下产生内力和变形。荷载结构法模型为2D单宽模型(图2)，衬砌结构采用梁结构单元进行模拟，侧墙及中隔墙分别离散为17段，底板及顶板分别离散为50段。侧墙水平向土压力按朗肯主动土压力施加，顶板铅直向土压力按上覆土层容重考虑，模型四周各施加仅受压(即受拉时失效)地基弹簧边界。

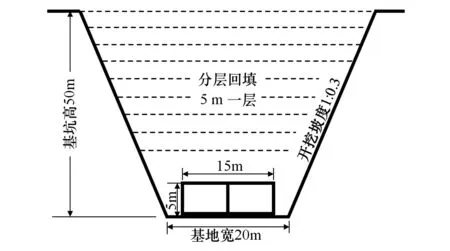
图1 标准断面图

表1 材料参数取值表

表2 地层-结构模型中回填土石的E-B模型参数表

荷载-结构法中，对于地基反力系数(又称地基弹性系数)是基于温克尔假定的弹性地基梁理论的表征地基弹性性质的参数，但由于温克尔假定本身是局部弹性理论，导致地基反力系数取值除与地基材料本身力学性能有关外，还随深度及地基形状/尺寸而变化。笔者采用文[6]中所建议的方法，根据泥岩刚度参数及管廊结构尺寸，折算地基反力系数取值为45 000 kN/m3。

2.3 地层-结构模型

地层-结构法将地下结构与地层作为一个受力变形的整体，按照连续介质力学原理来计算地下建筑结构以及周围地层的变形。考虑管廊结构轴向长度远大于其截面尺寸，地层-结构模型采用平面应变单元，泥岩地基、C30混凝土衬砌及回填土石均采用等参四节点实体单元(图3)，其中地基及衬砌采用线弹性本构关系，回填土石采用双曲线E-B本构关系，其加载切线模量Et、体积模量B、泊松比μ的表达式分别为：

图2 荷载-结构计算模型

(1)

(2)

(3)

式中k为切线模量基数；c为材料凝聚力；φ为材料的内摩擦角；Rf为材料破坏比；n为切线模量指数；Kb为体积模量系数；m为体积模量指数，上述参数由初始切线模量Ei与侧限压力σ3试验曲线确定的参数；Pa为大气压强。

计算中按荷载步分级回填，不计入地层自重产生的变形。建基面以下地基厚度150 m，左右边界据衬砌左右侧墙各100 m，底部及左右侧边界采用法向位移约束。

图3 地层-结构有限元模型(局部)

3 管廊衬砌结构特性

3.1 结构位移特征

逐级回填土石后，管廊整体在上部回填土石重量作用下逐渐下沉，以中隔墙底部沉降量值来看，荷载-结构法计算沉降位移为2.96 cm，地层-结构法计算沉降位移为3.76 cm。荷载-结构法甚至略小于地层结构法，该结果说明荷载-结构法中所考虑的地基反力系数已较为充分。

顶板跨中在回填土石重力作用下向下挠曲变形，底板跨中则在地基弹性抗力作用下向上挠曲变形，左右侧墙受到底板及顶部变形挤压效应影响，略向外侧挠曲变形。

对比荷载-结构法与地层-结构法顶部及底板最大挠度(图4)，两种方法对于底板挠度极值影响不大，回填至50 m厚度条件下底板最大挠度约-0.19 cm。但对于顶板挠度极值，地层-结构法结果(50 m回填厚度时-1.22 cm)则明显小于荷载-结构法结果(50 m回填厚度时-2.47 cm)。

图4 底板及顶板挠度极值随回填高度变化规律

3.2 结构应力特性

从衬砌顶板应力水平来看，无论是拉应力极值还是压应力极值，荷载-结构法计算结果均远大于地层-结构法计算结果(图5)。且荷载-结构法计算所得的拉压应力极值随回填深度增加而线性变化，地层-结构法逐渐呈随回填厚度增加应力增量有所减小的非线性变化趋势。从量值上来看，回填至15 m高度(顶板上覆土层厚度10 m)时，荷载-结构法所得的拉压应力极值分别为19.2 MPa和-20.15 MPa，而地层-结构法所得的拉压应力极值分别为5.5 MPa和-4.2 MPa，为荷载-结构法结果极值的28.6%和20.8%；回填至50 m高度(顶板上覆土层厚度45 m)时，荷载-结构法所得的拉压应力极值分别为80.9 MPa和-90.9 MPa，而地层-结构法所得的拉压应力极值分别为19.6 MPa和-14.3 MPa，为荷载-结构法结果极值的24.2%和15.7%。

3.3 基底应力特征值

从建基面基底平均应力量值来看，荷载-结构法与地层-结构法计算结果基本一致，均大致为-0.88 MPa。但荷载-结构法计算所得的基底最大应力远大于地层-结构法计算结果(图6)，50 m回填厚度时，地层-结构法基底最大应力量值为-1.46 MPa，荷载-结构法基底最大应力量值为-4.98 MPa。由于管廊结构本身刚度较为均匀，其与地基接触关系的不均匀性也较弱，基底应力沿建基面宽度方向变化分布应较为均匀，地层-结构法能够较好地模拟衬砌结构与地基的分载关系。

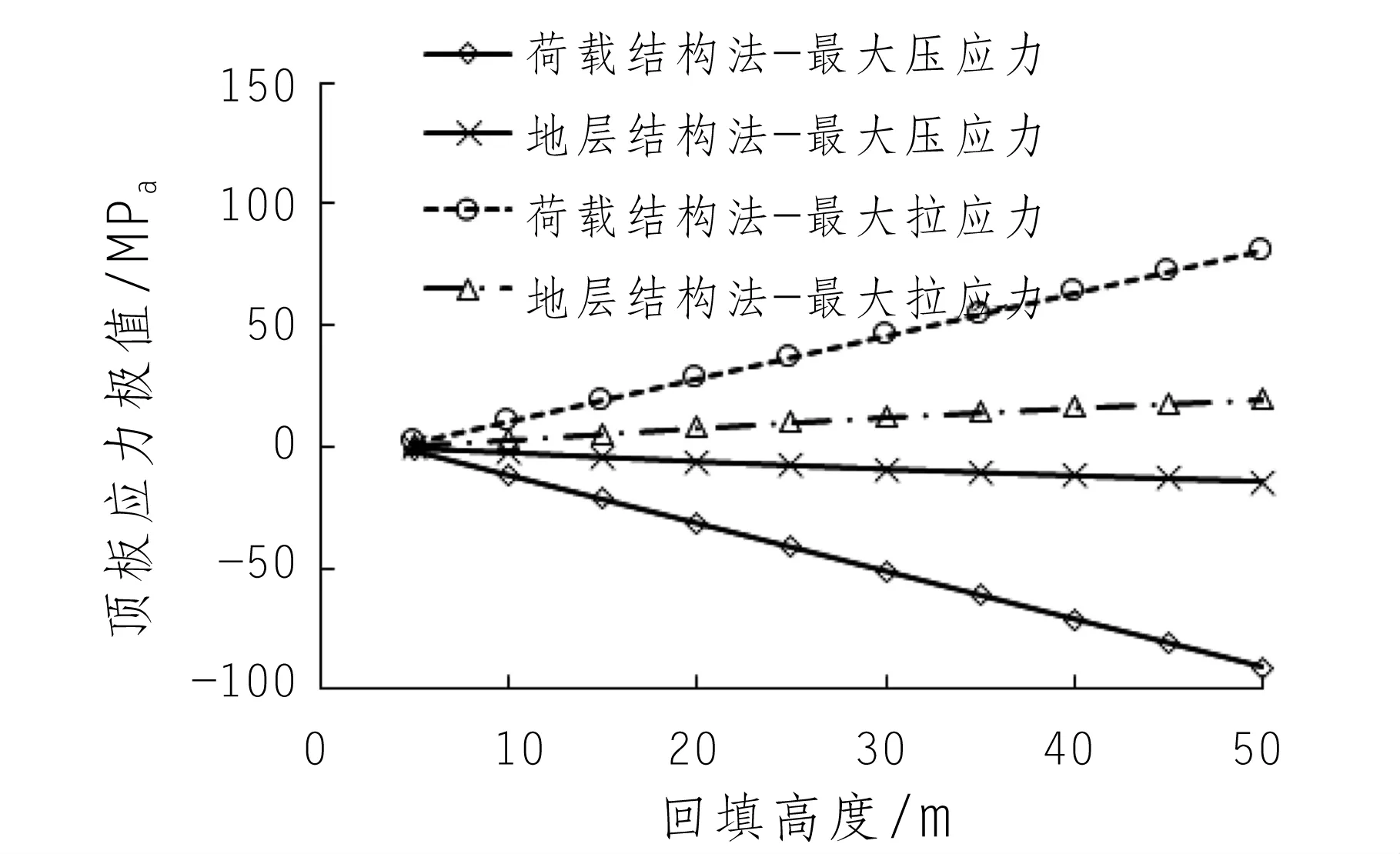
图5 顶板应力极值随回填高度变化规律

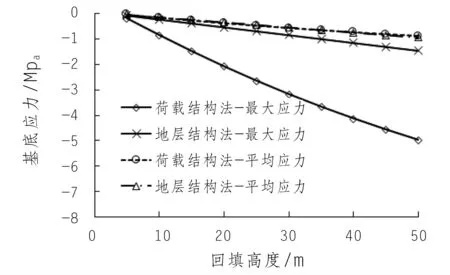
图6 基底应力随回填高度变化规律

3.4 分析比较

从受力方面来看，荷载-结构法的挠度与应力结果远大于地层-结构法的结果，这是由于荷载-结构法将地层与衬砌结构分开后荷载直接作用在结构上，所以结构受力较大，而地层-结构原理则是地层和结构共同承受荷载，衬砌变形也将引起地层应力重分布，分析结果相对更符合工程实际情况。

除此之外，虽然明挖暗埋法回填土石为散粒体结构，但其本身也存在抗剪强度性能(黏性土石甚至存在内聚力效应)，随着回填高度的增加，回填体将逐渐具有一定自承能力，将形成一定的拱效应或侧向摩阻效应，向下传递至衬砌的荷载比例将有所降低，这与地层-结构法所得的应力随回填高程呈非线性增长的现象是一致的。

4 结 语

笔者分别采用荷载-结构法与地层-结构法，计算分析了地下管廊结构特性随回填高度的变化规律。

(1)随着回填高度的增加，衬砌结构的挠度及应力、基底应力量值也将随之增加。但荷载-结构法计算结果明显大于地层-结构法结果，且荷载-结构法呈线性增长关系，而地层-结构法将呈现一定的非线性增长规律。

(2)荷载-结构模型仅用地基反力系数来模拟地基约束能力，该方法并不能很好地解决地层与衬砌相互作用这一非线性问题。地层-结构法将衬砌与地层视为整体共同受力的统一体系，在满足变形协调条件的前提下，不仅计算出衬砌结构的内力与变形，还同步计算地层应力及变形情况，充分体现周围地层与管廊结构的相互作用，其计算假设较少，计算结果也优于荷载-结构法。

(3)由于地层本身以及地层与管廊等结构相互作用模拟的复杂性，当前地层-结构法计算以有限单元法等数值计算方法为主，相关设计单位尚缺乏大量工程计算经验，建议今后设计阶段可同步使用荷载-结构法与地层-结构法，并根据工程监测数据对比分析，促进地层-结构法的推广应用，为综合管廊等地下建筑安全性与经济性平衡提供更有效支撑。