致密气藏压裂停泵振荡压力数据降噪处理技术研究及应用

李月丽，徐铜浩，龚郁峰

(1.中国石化华北油气分公司，河南 郑州 450006;2.成都理工大学，四川 成都 610059)

0 引言

致密油气藏水力压裂施工开采过程中，压裂液通过高压泵组泵入地层，当井底流压超过岩石破裂压力后，地层开始出现裂缝，通过加入一定浓度的支撑剂，形成一定长度的高导流裂缝，从而实现油气储层改造，提高单井产能的目的［1－2］，快速准确开展压裂后效果评价是目前的研究热点。压裂施工过程中，除支撑人工裂缝外，部分液体通过滤失进入地层，该过程与注水井的注入压降有类似之处，可以通过注入压降方法分析停泵压降数据，达到快速分析压裂施工效果的目的。然而，压裂停泵过程存在水锤现象，停泵压力数据会出现明显的低频振荡［3］，压力数据噪声大，对注入压降评价有一定的影响，因此，有必要对停泵压力数据进行降噪处理。停泵压降数据满足低通滤波信号特点，目前常用的去噪处理方法主要包括基于Savitzky－Golay滤波［4－5］、快速傅立叶变换［6］以及小波变换［7－8］3种。该文运用3种压力去噪处理方法，通过计算机程序对停泵水击振荡压力数据进行去噪处理，对比分析不同方法的去噪效果，并将优选的方法应用于大牛地某井，该井压裂施工结束后存在明显的停泵压降段，验证降噪处理方法的准确性。

1 停泵水击振荡压力降噪处理技术

1.1 基于Savitzky－Golay滤波的压力去噪处理

平滑滤波是波动压力分析中常用的预处理方法之一。Savitzky－Golay算法［9］被广泛地应用于数据流平滑除噪，是在时域范围内基于多项式并利用最小二乘法进行最佳拟合的方法。通过该方法可以极大程度保证原始数据不失真，方法更加简单、快捷。

Savitzky－Golay平滑公式为:

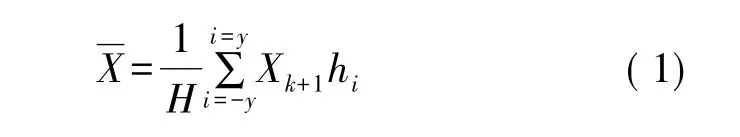
每一测量值乘以平滑系数hi的目的是尽可能减少平滑对有用信息的影响，从而改善平滑去噪算法的劣势［10］，hi/H可基于最小二乘原理，通过多项式拟合求得［11］。Savitzky－Golay卷积平滑关键在于矩阵算子的求解。设滤波窗口的宽度为l=2m+1，各测量点为 x=(－m，－m+1，…0，1，…，m－1，m)，其中，m为频率指数，采用 k－1次多项式对窗口内的数据点进行拟合。

图1为关井压降数据Savitzky－Golay滤波处理效果对比。由图1可知，现场实测压力存在较为杂乱的波动，主要是由于停泵之后，井筒内产生的水锤效应引起的。可以发现采用Savitzky－Golay滤波能够对停泵后水锤效应引起的压力波动进行有效的滤波，并达到工程可接受的效果。但是，尽管采用Savitzky－Golay滤波能够对停泵后压力曲线进行有效的平滑处理，但是压力振荡段滤波后的数据与原始数据存在一定的偏离。

图1 关井压降数据Savitzky－Golay滤波处理效果对比Fig.1 Comparison of the Savitzky－Golay filtering processing effect of shut－in pressure dropping data

1.2 基于快速傅立叶变换的压力去噪处理

虽然采用Savitzky－Golay滤波的方式能够对水锤引起的压力振荡进行有效的降噪处理，但是采用Savitzky－Golay滤波后的压力数据在振动幅度较大的区域内与实测数据存在一定的偏差，为了解决该问题，对停泵后压力数据进行了傅立叶变换滤波处理。目前，傅立叶变换是平稳层号处理最常用的一种方法［12］，最主要的原因是傅立叶变换的基所用的正弦波eaωt是所有线性时不变算子的特征向量，因而任何信号都能展开为若干正弦信号的叠加，即傅立叶变换是将信号从时域转换到频域［13］。在实际应用中，为便于利用计算机对信号进行分析，采集得到的信号一般都是离散信号。对已知连续信号x(t)，可以用采样间隔Δt的有限离散序列xn(nΔt)来表示，其中，n 为变换点数，n=0，1，2，3，…，N－1，N 表示信号的长度，因此，信号的离散傅立叶变换可以表示为:

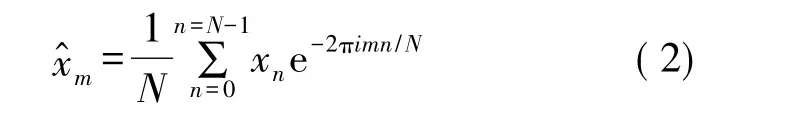
式中:xm为信号的离散傅立叶变换;xn为连续信号的未知量;N为信号的长度;a为复数单位;m为频率指数，m=0，1，2，3，…，N－1。

直接通过式(2)进行傅立叶变换需要计算的次数为2N，计算量很大。Cooley和Tukey提出了快速傅立叶变换(FFT)，使得计算量大大减少，约为N/2log2N。

图2为某测井压降曲线时间历程以及通过快速傅立叶变换滤波处理后的数据。由图2可知，采用快速傅立叶变换可以较为准确地对水锤产生的复杂压力波动振荡进行消除，进而得到较为平滑的压降曲线。采用快速傅立叶变换在处理特别复杂的工况时，在振荡剧烈段会得到较为理想的结果，但同时也将使平滑段产生虚假振荡。

图2 关井压降数据快速傅立叶变换滤波处理效果对比Fig.2 Comparison of the fast－Fourier－transform filtering processing effect of shut－in pressure dropping data

1.3 基于小波变换的压力去噪处理

克服上述快速傅立叶变换滤波传统方法带来的误差，提出采用小波变换滤波这一新的降噪处理方法，对井压降数据低频振荡信号进行滤波处理［14］。小波变换极大地克服了傅立叶和快速傅立叶变换的不足［15］，可以分析时变信号的局部特征。原则上讲，能用傅立叶变换分析的问题，都可以用小波变换来代替。

一个离散时间序列xn(t)的连续小波变换为:

式中:WT(s，t)为小波变换结果;*为复共轭;s为分辨尺度，m;t为时间;n'为时间平移量;Δt为采样间隔，s;ψ0为母小波;ψ为母小波ψ0无量纲化的结果［16］。

无量纲化处理是为了使每个尺度上的小波函数均有单位能量，方便小波变换后每个尺度的结果之间能够进行对比。

通过式(4)求解小波变换的计算量较大，根据卷积理论，可将其转换为计算xn(t)和ψ*傅立叶变换乘积的逆傅立叶变换:

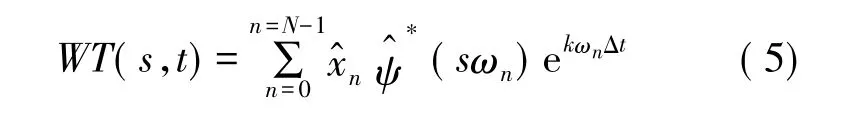
用式(6)实现连续小波变换，必须先选取合适的尺度。对尺度s的选取均采用二进制方法，即把尺度设为2的分数幂形式:

式中:sj是尺度数;j是尺度变量;so为可分辨的最小尺度，m;J为确定的最大尺度，m;δ为阈值。

so需恰当选择以便使相等的傅立叶周期近似于 2Δt，δj决定尺度数，最大不能超过 0.5，一个足够小的δj的选择依赖于小波方程谱空间的宽度。

连续小波变换的逆变换为:

式中:Cδ为重构系数;Wδ(s)为母小波各个尺度计算结果;Re为复数的实部。

其中，如果采用的母小波为复数形式，xnA(t)表示xn(t)解析信号，实部是xn(t)，虚部与Hilbert变换的结果一样。另外如果只对其中部分尺度感兴趣，可以只计算这些尺度上的结果，这样也叫做滤波。

图3为关井压降数据小波变换滤波处理效果对比。由图3可知，采用小波变换方法对由停泵产生水锤效应而导致的压力波动进行滤波，可以得到令人满意的结果。经小波变换滤波后的数据在波动剧烈段和压力平稳段均为非常平滑的数据，表明采用小波变换滤波的方法可以对复杂的压力波动现象进行滤波，得到理想的压降曲线［17－24］。

图3 关井压降数据小波变换滤波处理效果对比图Fig.3 Comparison of wavelet－transform filtering processing effect of shut－in pressure dropping data

2 去噪处理方法的优选

图4为3种滤波方法与实测数据的对比。由图4可知，Savitzky－Golay滤波得到的校正压力在压力迅速降低段与实测压力存在一定的差距，相对误差达到5.3%。快速傅立叶变换得到的校正压力在压力平稳段存在一定幅度的波动，与实测压力数据有一定的差距。小波变换得到的校正压力与实测压力总体上吻合非常好，相对误差只有0.4%，满足了注入压降分析精度要求。因此，建议采用小波变换滤波算法进行停泵压降数据的预处理工作。

图4 3种滤波方法与实测数据对比Fig.4 Comparison of the three filtering methods and the measured data

3 压力去噪技术在压裂效果评估中的应用

X1井为鄂尔多斯盆地伊陕斜坡东北部构造带上的一口开发井，完钻层位为石炭系太原组，地面海拔为1 304.52 m，完钻层位为石炭系太原组，完钻井深为2 925.00 m。图5为X1井压裂施工曲线。由图5可知:施工结束后存在明显的停泵压降段，因此，利用压裂施工数据去噪算法，对停泵数据进行了去噪处理，并开展了注入压降评价。

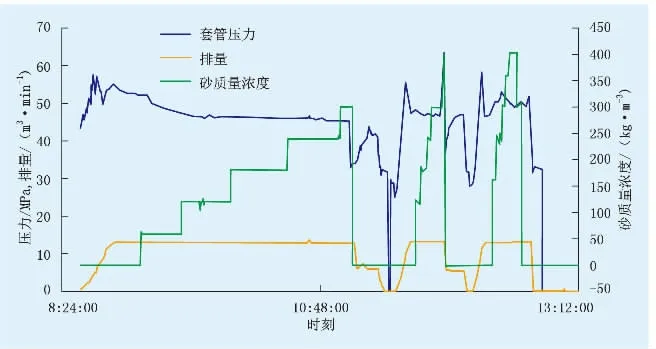
图5 X1井压裂施工曲线Fig.5 Fracturing curve of Well X1

图6为X1井第9段停泵后压力变化曲线及采用小波变换滤波后的压力曲线。由图6可知:采用小波变换滤波处理后的压力曲线在停泵前、压力迅速下降段、压力波动较大段以及压力平稳段均能够很好的对实测数据进行拟合，小波变换滤波在停泵水击振荡压力降噪中具有良好的效果。

图6 X1井压降数据小波变换滤波处理效果对比Fig.6 Comparison of the wavelet－transform filtering processing effect of pressure dropping data from well X1

通过注入压降分析，获得停泵压裂双对数曲线(图7)，该曲线压力导数曲线上翘，呈现斜率为0.25的有限裂缝导流渗流模式，解释表皮系数为0.385，渗透率为1.56 mD，解释缝长为29.4 m，压裂后试气无阻流量为23.6×104m3，表明该井水力压裂施工较为成功，与分析结果较为吻合。

图7 X1井压裂停泵后双对数曲线Fig.7 Double logarithmic curve of well X1 after stopping pump during fracturing

4 结论

(1)Savitzky－Golay滤波得到的校正压力在压力迅速降低段与实测压力有一定的差距，相对误差达到5.3%;快速傅立叶变换得到的校正压力在压力平稳段存在一定幅度的波动，与实测压力数据有一定差距;而小波变换得到的校正压力与实测压力总体上吻合非常好，相对误差只有0.4%，满足注入压降分析精度要求。

(2)停泵压裂双对数曲线为有限裂缝导流渗流模式，斜率为0.25，解释表皮系数为0.385，渗透率为1.56 mD，解释缝长为29.4 m，压裂后试气无阻流量为23.6×104m3，与分析结果较为吻合，表明该井水力压裂施工较为成功。