基于LHS抽样的边坡可靠度有限元分析

曹 伟，李文静，易海洋，王野驰，张红芬

(1. 华北科技学院 建筑工程学院，北京 东燕郊065201； 2. 北京航空航天大学 交通科学与工程学院，北京100191；3. 燕京理工学院 建筑学院，北京101601)

0 引言

滑坡是一种常见的地质灾害，其稳定性评价一直是岩土工程界的重点研究课题。传统的边坡稳定分析方法假定土体的参数是一个定值，根据极限平衡法计算出安全系数，进而进行边坡的稳定性评价。然而实际的岩土工程问题往往具有的一定的不确定性，为了考虑这些不确定性，可靠度方法被用于边坡的稳定性分析[1-3]。该方法可以考虑土体参数的变异性和相关性，更符合岩土工程实际，因此越来越受到岩土工程界的关注，并逐渐成为一种趋势[4]。常用的可靠度分析方法有一次二阶矩法、概率矩点估计法、响应面法及Monte Carlo模拟法等[5]。随着计算机技术的发展，随机分析理论与有限元法相互结合，形成了随机有限元方法。随机有限元方法采用强度折减法计算边坡的安全系数，不需要预先假定临界破坏面，被广泛应用于边坡工程的可靠度分析[6]。

近年来，国内外进行了很多边坡可靠度方面的研究，取得了大量的研究成果。Lumb[7]在大量土工试验的基础上，提出大多数土体的参数都可以看作正态分布的随机变量来考虑，并将可靠度的方法应用于边坡的设计和稳定性评价。Nguyen[8]提出了一种具有相关随机变量的Monte Carlo模拟方法，将其应用于岩土工程的风险分析，并取得了很好地模拟效果。Griffiths和 Fenton将有限元强度折减法与随机场理论结合，提出随机有限元的方法用于边坡的可靠度分析[9-10]。杨明、孙小娜、陈将宏等利用Monte Carlo法，采用MATLAB软件编制了程序，实现对土质边坡稳定的可靠度分析，研究了土体参数变异性对边坡稳定性的影响[11-13]。朱瑜劼等[14]基于Monte Carlo法和GEO-SLOPE软件，对三峡库区泄滩边坡的稳定性进行了综合评价，并对其进行支护设计。李典庆等[4，15，16]提出了非侵入式的随机有限元法，用于计算考虑土体参数空间变异性的边坡可靠度。该方法的计算程序NISFEM用MATLAB 语言编写，并将GEO-SLOPE软件视为黑箱子直接调用。

在上述研究中，采用MATLAB软件编制的程序和岩土数值分析软件GEO-SLOPE计算边坡稳定性都是基于极限平衡方法的，均需要事先假定临界破坏面。相比较而言，ABAQUS、ANSYS等有限元软件基于强度折减法计算边坡的稳定性，无需事先假定临界破坏面，更符合实际情况，适用性更强。传统的Monte Carlo抽样方法收敛速度慢，需要较大的模拟次数，计算量非常大，而LHS抽样可以使用较少的模拟次数达到收敛标准，从而提高抽样的效率。目前现有的有限元软件不能考虑参数的变异性和相关性，也没有内置LHS抽样方法，不能直接进行用于可靠度分析，因此在使用这些软件计算边坡可靠度时需要其他软件协同合作，不仅开发难度大，也难以进行推广[17]。

本文基于LHS抽样在有限元软件ABAQUS中开发了边坡可靠度自动计算的算法，用户可以通过交互输入参数调整土体的变异性和相关性，即可简单方便地计算出边坡的可靠度。通过典型的边坡算例，利用开发的算法计算了边坡的可靠度，并对可靠度的影响因素进行了分析。

1 边坡可靠度分析的有限元-LHS法

1.1 有限元强度折减法

有限元强度折减法最早由Zienkiewicz等提出，已经在边坡工程中得到了广泛应用。与极限平衡法相比，有限元强度折减法[18-19]考虑了土体的非线性弹塑性本构关系以及变形对应力的影响，而且能够模拟边坡的失稳过程及其滑动面形状，无需提前对滑动面形状和条块条间力(无需进行条分)作任何假定。该方法通过将岩土体抗剪强度参数逐渐降低直到边坡失稳破坏，以临界破坏的强度折减系数作为边坡安全系数[20]。本文采用摩尔-库伦强度模型，假定抗剪强度折减系数为Fr，为在计算过程中，将土体抗剪强度参数按照下面的公式进行折减：

(1)

(2)

式中，c和φ为土体的粘聚力和内摩擦角；c′和φ′为折减后土体的粘聚力和内摩擦角。

1.2 有限元-LHS法

拉丁超立方抽样法(LHS)是一种分层抽样方法。与传统的Monte Carlo 抽样法相比，LHS抽样法更高效，能够做到以较小的采样规模获得较高的采样精度。在边坡的可靠性分析中，可以将LHS抽样法与有限元强度折减法结合起来，以Z=Fs-1作为边坡的功能函数，先按照土体材料参数的分布函数生成n组随机数(c1，φ1)，(c2，φ2)，…，(cn，φn)，把生成的n组随机数作为土体的材料参数，采用有限元强度折减法分别计算边坡的安全系数，从而得到安全系数的n个相对独立的统计样本值Fs1，Fs2，… ，Fsn。统计安全系数的样本中满足Fs<1的个数，假设为m。那么当n足够大时，由大数定律可知边坡的失效概率为：

(3)

由安全系数的统计样本可以较精确地得到安全系数的概率分布及其分布函数。安全系数的均值和标准差分别为：

(4)

(5)

若用β表示可靠指标，并定义β=μZ/σZ，则失效概率：Pf=1-Φ(β)，其中Φ(β)为标准正态分布函数。

2 边坡可靠度自动计算流程

2.1 确定性分析模型的建立

在ABAQUS软件中建立边坡稳定性的确定性分析模型，包括绘制边坡剖面、赋予材料参数、划分网格、设置荷载和边界条件、设定分析步、通过场变量实现强度折减法进行计算等步骤。其中土的强度采用摩尔-库伦模型，土体参数取均值。为了检验确定性分析模型的正确性，建立Job-0，并提交运算，查看计算得到的安全系数，并与其他稳定性分析方法的计算结果进行对比。

2.2 输入可靠度计算所需要的参数

可靠度计算需要输入的参数有粘聚力c的均值和变异系数、内摩擦角φ的均值和变异系数、c与φ的相关系数和LHS的模拟次数N等。为了方便用户操作，在ABAQUS中利用Python语言开发了可靠度计算所需参数的接口。在ABAQUS软件中打开建立好的边坡确定性分析模型，然后运行脚本Parameters.py，在如图1所示的窗口中就可以输入这些计算参数，输入参数以后，单击“OK”键即可。

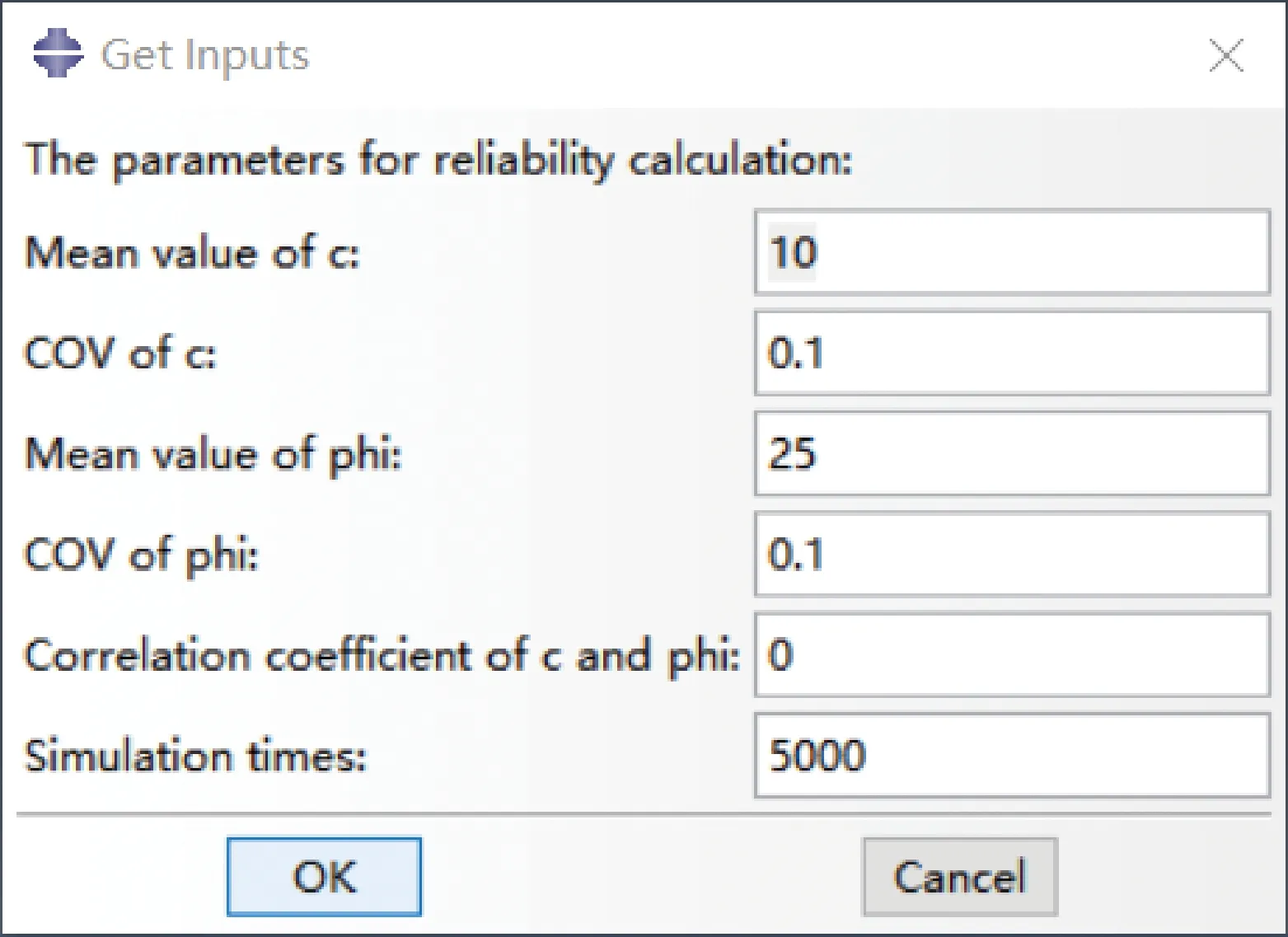
图1 边坡可靠度计算参数的输入窗口

2.3 计算边坡的可靠度

在ABAQUS软件中运行Calculation.py脚本，ABAQUS会开始自动计算边坡的可靠度，并将计算得到的多个安全系数样本值和边坡失效概率等结果输出到文件中。程序的求解过程如图2所示。

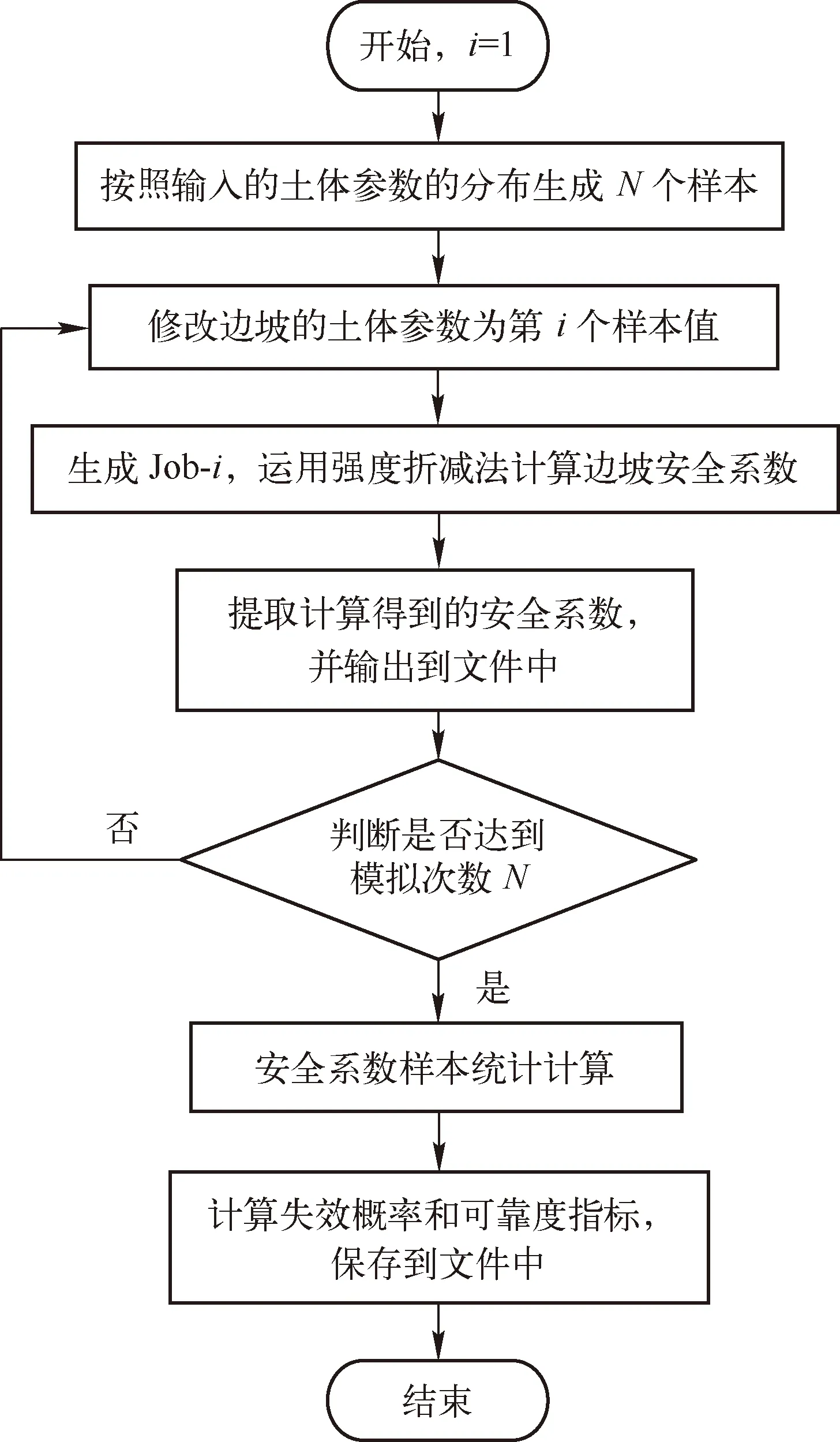
图2 边坡可靠度计算流程图

3 算例分析

下面以图3所示的边坡为算例，利用开发的可靠度计算算法进行分析。在有限元软件ABAQUS中建立边坡的强度折减计算模型，边坡的坡高为 10 m，坡度为 1∶1。单元采用平面应变单元CPE4，共划分成1210个单元。土体参数统计特征见表1，先取土的材料参数为其均值，计算得到边坡的安全系数，并与经典的边坡稳定分析方法的计算结果进行对比。通过表2可知，由ABAQUS强度折减法计算出的边坡安全系数与其他三种经典方法的结果基本一致，说明采用强度折减法计算边坡安全系数是较为准确的。

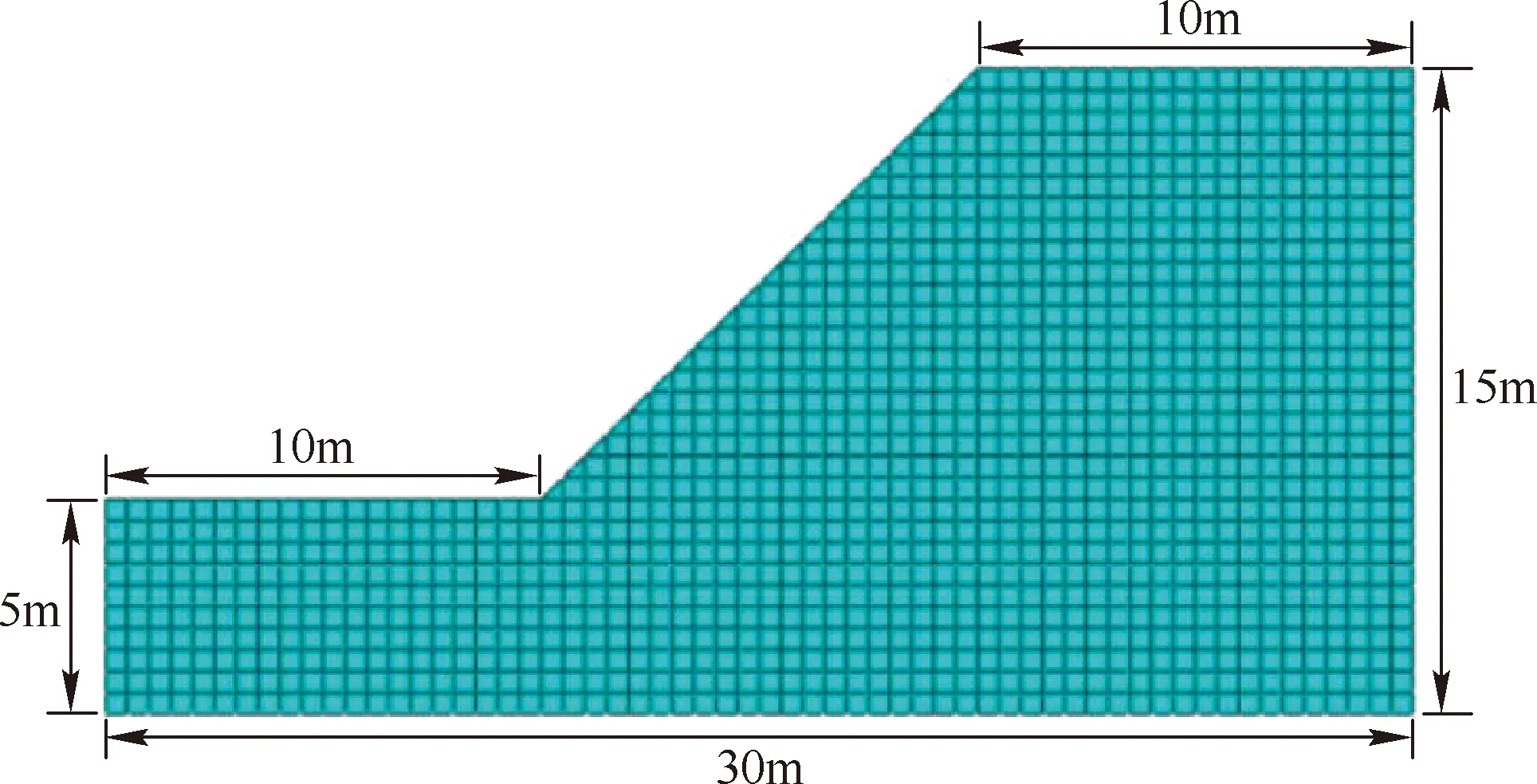
图3 边坡的有限元计算模型

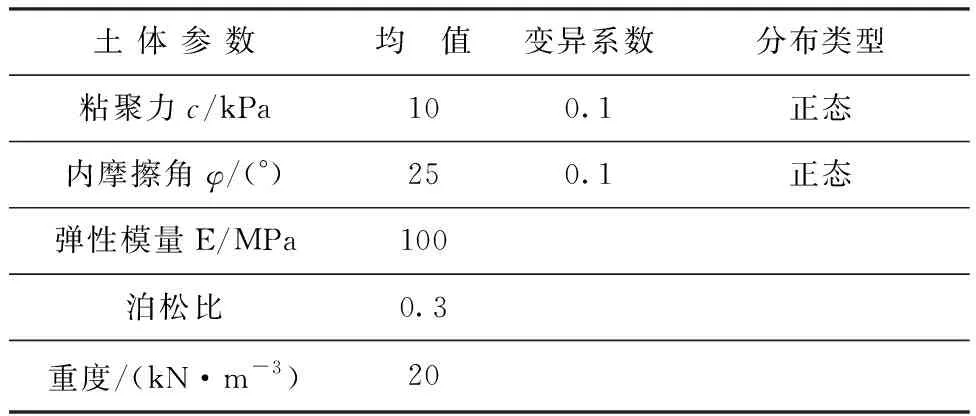
表1 土体参数统计特征

表2 边坡安全系数结果对比

3.1 边坡可靠度的计算

取LHS模拟次数为5 000 次，利用在ABAQUS中开发的边坡可靠度计算算法进行计算，得到安全系数样本的散点图如图4(a)所示，可见安全系数大多分布在0.95～1.25之间。经过统计可知，安全系数的均值为1.082，标准差为0.083，变异系数为0.077。可见安全系数的变异系数要小于粘聚力和内摩擦角的变异系数0.10。进一步计算得到，边坡的失效概率为20.12%，对应的可靠性指标为0.8373。通过如图4(b)所示的安全系数样本的分布直方图可以发现，安全系数近似服从正态分布。

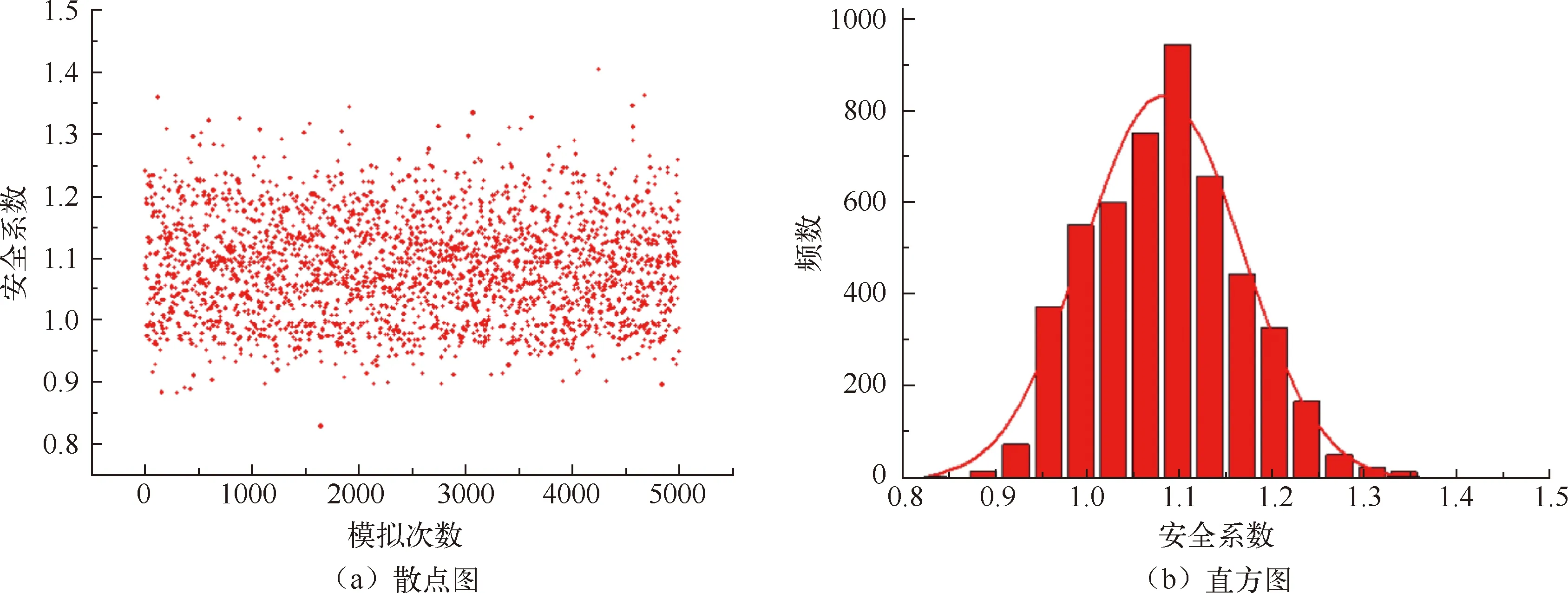
图4 安全系数样本分布图

3.2 边坡可靠度影响因素分析

在利用开发的边坡可靠度算法进行计算时，LHS模拟次数、土体参数变异性、土体参数相关性等因素对可靠度的计算结果均有影响，但影响大小不同。下面对这些边坡可靠度的影响因素的进行研究。

3.2.1 模拟次数

取模拟次数100、250、500、750、1 000、2 000、3 000、4 000、5 000，分别计算边坡的安全系数的样本，统计得到安全系数样本的均值、标准差、失效概率和可靠度指标等，分析模拟次数对于边坡可靠度的影响。

如图5所示，安全系数的均值、标准差、失效概率和可靠度指标均随着模拟次数的增加趋向于稳定。当采用LHS抽样法时，在模拟次数达到1 000 次以上时，各项指标已基本稳定。而Monte Carlo 抽样法当模拟次数达到3 000 次以上时，才趋于稳定。这表明LHS抽样法比传统Monte Carlo 抽样法更高效，可以明显的减少计算的工作量，更适用于计算边坡的可靠度问题。

图5 模拟次数对计算结果的影响

3.2.2 土体参数变异性

为了研究土体参数变异性对边坡可靠度的影响，固定c和φ中的一个土体参数为其均值，另一个参数取不同变异系数的正态分布，LHS模拟次数为1 000 次，分别计算边坡安全系数的样本和可靠度，得到的结果如图6所示。

由图6可知，土体参数的变异性对于安全系数的均值几乎无影响，安全系数的均值始终稳定在1.084附近。安全系数的标准差随着土体参数的变异系数增加而增加，相对而言，在变异系数相同的条件下，内摩擦角φ变化对应的安全系数标准差要大于粘聚力c变化对应的安全系数标准差，说明内摩擦角对于边坡稳定性的影响要大于粘聚力。随着土体参数变异系数的增加，失效概率Pf逐渐增加，对应的可靠度指标β逐渐降低。除去变异系数小于0.08的范围之外，内摩擦角φ变化对应的可靠度指标β均小于粘聚力c变化对应的可靠度指标β。当变异系数小于0.15时，内摩擦角φ变化引起的可靠度指标β的下降幅度要大于粘聚力c，说明可靠度指标β对于内摩擦角φ变化更加敏感。当变异系数大于0.15时，内摩擦角φ变化与粘聚力c变化引起的可靠度指标β的下降幅度大致相同。

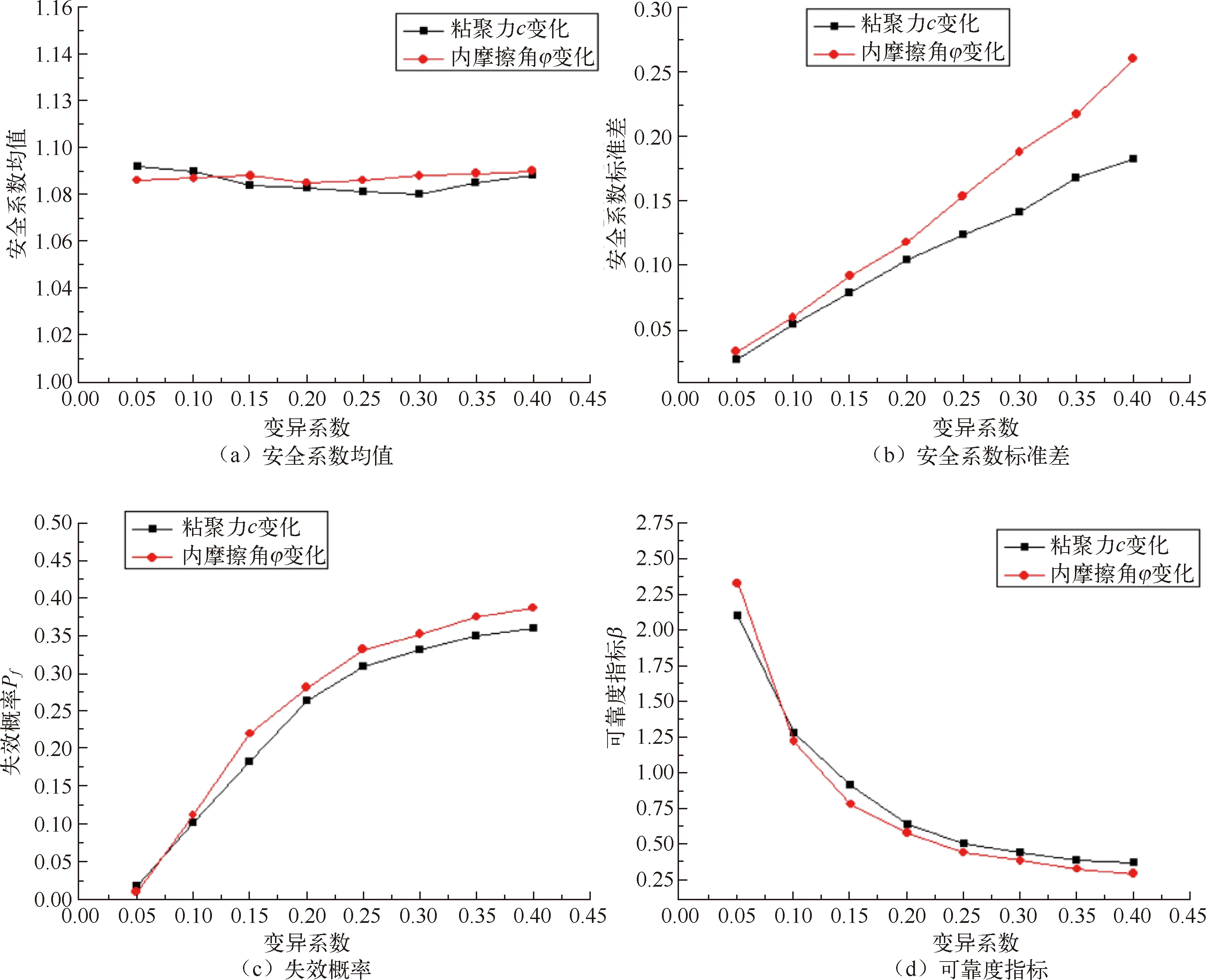
图6 土体参数变异性对计算结果的影响

3.2.3 土体参数相关性

在实际的边坡中，土体参数并不是独立随机变量，而是具有一定的相关性，这种相关性会对边坡的可靠度分析产生一定影响。对上述算例，取不同的相关系数，生成多个c、φ相关性不同的土体参数样本，利用开发的可靠度算法分别计算边坡的可靠度，研究c、φ相关性对边坡可靠度的影响。计算得到的边坡可靠度指标β随相关系数的变化关系见图7。当相关系数从-0.75变到0.75时，可靠度指标β从1.55降低到了0.61，对应的失效概率Pf从6.1%增加到了27.2%。可以看出，c、φ的相关性对边坡可靠度具有明显的影响。c和φ的负相关性对边坡的稳定性是有利的，对应的可靠度指标β较高；相应的，当c和φ呈正相关时，若忽略变量的相关性，所得可靠度指标高估了实际值，偏于不安全。在进行边坡的可靠度分析时，要尽可能准确地确定c和φ的相关性，从而得到更符合实际的结果。

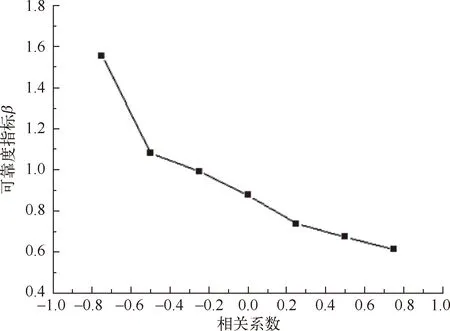
图7 可靠度指标β随相关系数的变化

4 结论

(1) 开发的边坡可靠度自动计算算法是可靠的，用户可以通过交互输入参数，方便准确地计算出边坡的可靠度，解决了传统可靠度计算需要多种软件协同合作的难题。

(2) 模拟次数、土体参数变异性和c、φ的相关性对于可靠度的计算均有明显的影响。边坡可靠度随着模拟次数的增加趋于稳定，并且在计算边坡可靠度时，LHS抽样法比传统Monte Carlo 抽样法更为高效。当采用LHS法，模拟次数达到1 000 次以上时，计算出的可靠度较为准确。可靠度指标β与土体参数变异系数呈负相关，随着土体参数变异系数的增加，可靠度指标β逐渐降低。相对而言，可靠度指标β对于内摩擦角变化更加敏感。c、φ的负相关性对边坡的稳定性是有利的，负相关性越强，边坡的可靠度越高。