基于Transformer模型和Kalman滤波预测船舶航迹

徐瑞龙 祁云嵩 石 琳

(江苏科技大学计算机学院 江苏 镇江 212003)

0 引 言

海洋不仅是国际贸易和大宗货物运输的主要通道，也是未来维护国家权益和安全的主要领域，海洋已经成为人类生存的第二大空间。有效地对船舶航迹及时预测、跟踪是解决海上交通的核心问题，所以对其深入研究非常有必要，而且目前对航迹状态估计预测的研究已经有很多。姜佰辰等[1]提出了一种基于多项式Kalman滤波的船舶轨迹预测算法，补偿航迹定位数据信息缺失、更新较慢等问题，并基于经纬度信息预测船舶运动轨迹。文献[2]利用以时间序列为基础的轨迹数据，预测船舶航行轨迹的线性运动，在丢失部分航迹数据的情况下仍可以取得良好的预测效果。但是实际情况下，船舶航迹一般都是动态变化、非线性的，很难满足线性需求。文献[3-4]分别是通过支持向量机的方法和利用灰色模型结合马尔可夫链对航行轨迹数据进行时间序列上的预测，然而二者都需要预先通过专家知识构建运动学方程，面对复杂的实际航迹相对难以实现。乔少杰等[5]利用系统状态空间模型、观测模型，以最小均方误差为准则结合Kalman滤波，针对移动对象的行为，利用前一时刻的估计值和当前时刻的观测值更新对状态变量的估计,预测出下一时刻轨迹位置。文献[6]提出了一种处理函数型数据的现代统计方法，即高斯过程回归。该方法在充分利用所给数据的前提下进一步总结数据本身的时间、周期和增减趋势，以此建立模型预测船舶轨迹。文献[7]提出了基于高斯混合模型的轨迹预测方法，针对复杂的运动模式利用高斯混合模型建模,并通过模型计算不同运动模式的概率分布,将轨迹数据划分为不同分量，实现准确和高效的位置预测。文献[8]利用AIS数据的航行轨迹特征，提出了循环神经网络——长短期记忆模型(Recurrent Neural Networks-Long Short Term Memory,RNN-LSTM)，通过训练模型，预测未来船舶航行轨迹。

综上所述，海域环境极其复杂，干扰的随机性、多样性导致船舶运动状态往往频繁变化，状态信息无规律可寻，难以准确提取特征数据变化趋势。另外，部分算法无法满足时间序列要求、实时性要求，而且实时准确地建立航迹数学模型极其困难，难以用简单的模型进行推算。本文提出基于Transformer深度学习模型结合Kalman滤波器的方法进行航迹预测。该方法充分发挥Transformer模型突出的特征提取能力和高效的并行运算效率[9-10]，将船舶历史航迹特征数据作为模型输入进行训练预测，同时利用Kalman滤波器对预测值进行实时调整，实现最优估计值。

1 相关概念及模型

传统深度学习算法如RNN、LSTM，它们都是顺序计算，即相关算法只能从左向右依次计算或者从右向左依次计算，这样会导致两个问题：①t时刻的计算依赖于前一时刻的值，限制了模型并行能力[11]；② 计算过程的信息丢失问题，虽然LSTM算法一定程度上缓冲了这个情况，但对于超长期的依赖，LSTM还是会存在问题[12]。Transformer模型摆脱了传统的卷积神经网络和循环神经网络结构[13]，整个网络架构是由注意力机制组成，完全利用自注意力机制(self-Attention)和前馈神经网络(Feedforward Neural Network,FNN)对样本进行“自我学习”和“自我调整”，省去利用先验知识处理的步骤，而且其并行能力突出，高于传统的RNN算法，对于航迹预测问题有一个很好的解决效果。但是Transformer的静态预测可能无法兼顾航迹当前值的变化，为降低其对预测结果的影响，利用Kalman增益，使用当前值对预测值进行实时动态修正，实现进一步提高预测精度。

1.1 自注意力简介

Transformer模型注意力机制的思想核心是计算输入向量列表中每个样本与该向量中所有样本的关联情况，并利用这种相互关系在一定程度上体现不同样本的重要程度，通过这种关联程度调整每个样本的权重，从而获得一个更加全局的表达，不仅考虑到样本自身，同时还将其与其他样本的关系融入在内。Transformer模型本质是一个编解码器的结构，解码器的输入为编码器的输出。编码器由N个编码层组成，并且每层是完全相同的，同样对应的解码器也是由N个相同的解码层构成。图1给出了单个编码器和自注意力机制的结构。

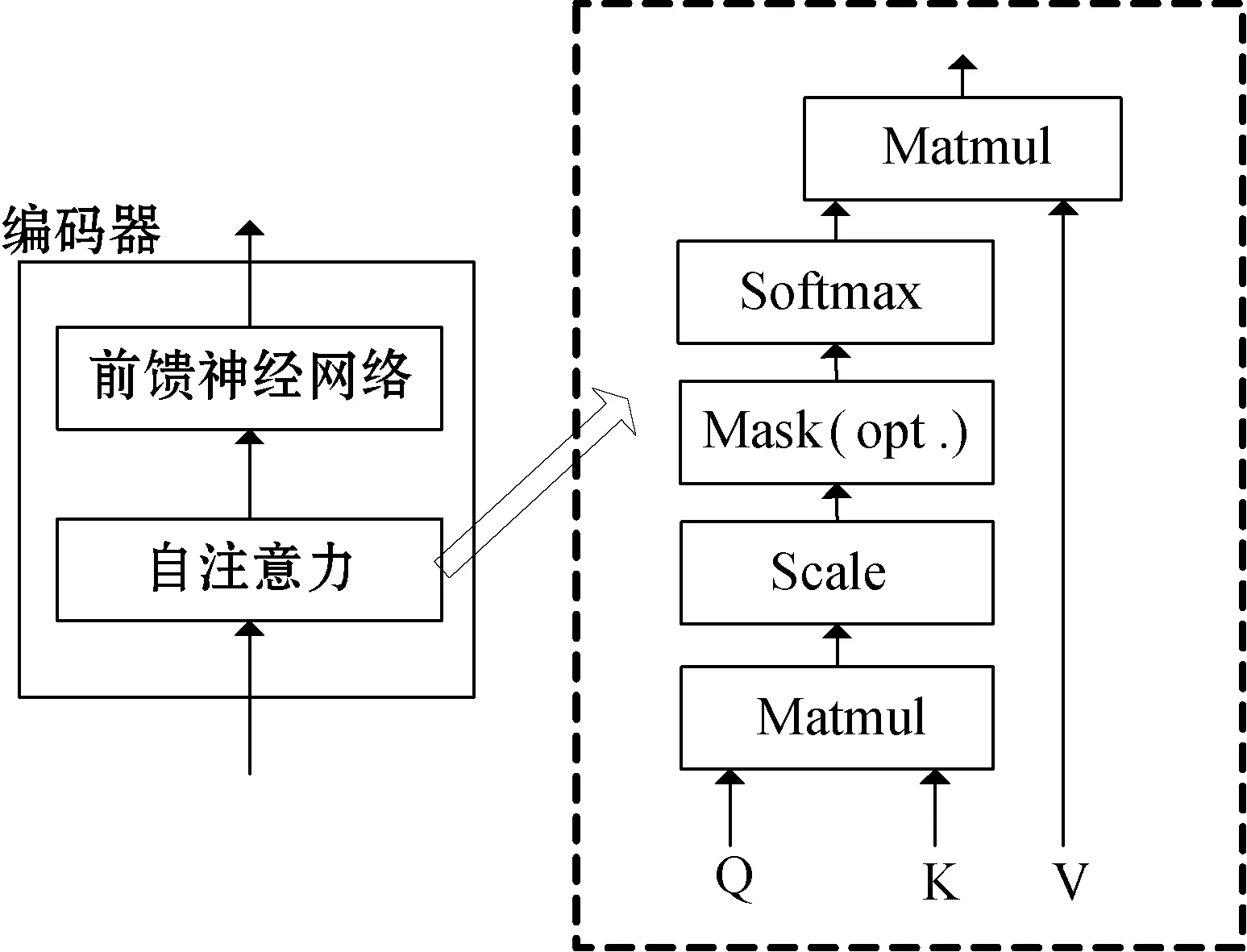
图1 编码器和自注意力机制

假设输入集为X={x1,x2,…,xt,xt+1,…}，其中t为时间序列{t|t=1,2,…,T}，编码器将输入集作为一个向量列表输入，经过存在依赖关系的各自路径进入注意力层，同时通过将向量中每个样本点积训练过程中创建的3个训练矩阵(WQ,WK,WV)，为每个样本生成三个诠释向量，即查询向量(Q)、键向量(K)、值向量(V)。注意力机制实现具体步骤如下。

步骤1获取三个诠释向量，计算式分别表示为:

(1)

步骤2为每个样本打分，计算式表示为:

(2)

viuj=cos(vi,uj)‖vi‖2‖uj‖2

(3)

式中：v、u分别为Q、K的投影。

步骤3优化训练梯度，计算式表示为:

(4)

式中：D(K)表示K向量的维度;dk为梯度因子，其值由经验所得并非唯一值。

步骤4利用Softmax函数进行标准化，并将标准化后的值与向量V进行点积运算，保证在保持对当前样本关注度不变的情况下，降低对不重要样本的关注度[14]，获取自注意力机制输出，计算式表示为：

Attention(Q,K,V)=Softmax(Opt)·V

(5)

步骤5通过残差连接进行归一化处理，得出注意力层的输出，并作为前馈神经网络的输入。层归一化在稳定循环网络中的隐藏状态动态方面非常有效，可以大量减少训练时间而且每个样本对应的前馈神经网络是完全一样的，在此层可以用并行化提高效率，使得Transformer模型效率高于传统深度学习模型。

1.2 Kalman滤波

Kalman滤波是一种线性最优滤波算法，适合于线性高斯系统，其不要求保存过去的量测数据，根据当前数据和前一时刻数据的估值，根据系统状态方程，使用Kalman增益进行修正，预测出新的状态估计值[15-16]。假设船舶航行轨迹在t时刻的状态为：

X(t)=[x,y,v,α]

(6)

式中：x、y分别表示由经纬度转换后的直角坐标系坐标值；v表示航速；α表示当前时刻对地航向。

模型状态方程与量测方程分别为：

X(k+1)=FX(k)+Bμ(k+1)+ω(k+1)

(7)

Z(k+1)=HX(k+1)+V(k+1)

(8)

式中：X(k+1)表示航迹在k+1时刻的状态向量;Z(k+1)表示在k+1时刻的量测向量;F为状态转移矩阵;B为过程噪声或控制矩阵;H为量测矩阵或量测值系数矩阵；μ(k+1)为k+1时刻对系统的控制量，若当前状态没有，可以为0；ω(k+1)和V(k+1)分别为过程噪声和量测噪声，且都为相互独立、均值为0的高斯白噪声。

Kalman滤波器修正步骤如下：

(9)

(10)

(11)

(12)

(13)

2 船舶航迹预测模型

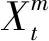
(14)

式中：m代表MMSI，为方便计算，将经纬度转换为直角坐标系值，即x、y;则x、y、v、α、dt分别代表t时刻m号船舶的坐标、航速、航向、时间间隔。

图2 具体模型结构

步骤1位置编码，采用偶数位置进行正弦编码，奇数位置进行余弦编码；通过位置编码解释样本中元素序列的顺序问题[17-18]，计算式如下：

(15)

(16)

式中：pos表示样本中元素位置;i表示样本中元素的维度；dmodel表示位置向量的维度，与整个模型的隐藏状态维度值相同。

步骤2应用Attention机制，计算输入向量列表的诠释向量Q、K相似度，并利用激活函数Softmax进行归一化，最后利用V进行加权求和，从而实现对各个样本合理的关注度，然后经过线性变换和Softmax层输出预测结果，如式(1)-式(5)所示。但是Attention机制无法避免数据本身存在的问题，航迹的历史数据中也会存在一些偏离航道的轨迹数据，这会对模型预测造成一定的误差，故提出将数据中未偏离航道点迹数和总点迹数的占比，点积模型输出，再进行归一化，加权求和以降低预测的偏差，计算式表示如下：

(17)

(18)

式中：nleg表示样本向量中未偏离航道的航迹点数；Ntr表示样本向量的总航迹点数；f(Q,K)表示Q、K的相似度。

步骤3多头注意力机制，利用h个不同的线性变换对Q、K、V进行投影，将不同的注意力机制结果拼接起来，获取多头注意力机制的输出，计算式表示如下：

(19)

MulHead=Concat(head1,head2,…,headh)Wo

(20)

式中：Concat表示将多个Attention结果进行拼接。

步骤4前馈神经网络层计算，经过多头注意力机制、归一化处理后的样本会进入一个全连接的前馈神经网络，输出表示为：

FFN(Z)=max(0,ZW1+b1)W2+b2

(21)

式中：b表示偏置。

步骤5子层输出，每个编码器由两个子层(sub)组成：多头自注意力和前馈神经网络。每两个子层中都会使用一个残差连接进行归一化操作[19-20]。每个子层的输出可以用式(22)表示：

sOut=LN(x+sOut(x))

(22)

(23)

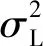
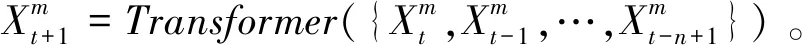
B(k+1)=Z(k+1)-Z(k+1,k)

(24)

(25)

图3 自调整Kalman滤波器

根据上述描述步骤，结合Transformer模型和Kalman滤波器的航迹预测过程，算法描述如下：

算法1基于Transformer模型和Kalman滤波预测算法

输出：预测航迹均方误差MSE。

1.X′=Dev_Norm(Xtrain)；

2.X*=NData_to_supervised(X′)；

5. fori=1 tot

6.p_t=TF_Predic(TF)；

7.pVal=Kalman(p_t)；

8.err[i]=getError(m,pVal)；

9.init_Kalman(pVal,err[i])；

10. end

算法1中：NData_to_supervised为构建监督学习数据集函数；Dev_Norm为离差归一化函数；TF_Predic为加入未偏离航迹权重的Tranformer模型；变量err为航迹点误差值；变量p_t为Transformer模型预测值；pVal为最终预测值。

3 实验与结果分析

本文采用宁波市水域内3 000组船舶AIS信息数据作为实验数据，并抽取其中200组作为测试数据，验证基于Transformer模型和Kalman滤波器的航迹预测模型(下文简称为TK模型)的有效性。实验使用Python 3.5版本，基于TensorFlow 1.12实现本文算法。

Transformer模型参数设置：编解码为8层；隐藏层神经元数量hidden_size为512；batch_size为500；dk为64；dmodel为512；dropout为0.1。

Kalman模型参数设置：R=[20,0;0,20];Q=[20,0,0,0;0,20,0,0;0,0,20,0;0,0,0,20]。

实验的硬件条件：CPU为Intel(R) Core(TM) i7-8550U，主频为4.0 GHz，内存为8 GB。

3.1 算法预测

算法实验以宁波市MMSI号为412999999的渔船为例，对其坐标位置进行预测，通过对比量测和预测的航迹图，可以更直观看出预测效果，如图4所示。图4(a)展示了量测航迹与预测航迹整体情况，可以明显地看出二者航迹线几乎重叠。图4(b)为此航迹预测部分细节图，图中的量测与预测的坐标位置点误差偏移很小，证明了算法预测精度较高。

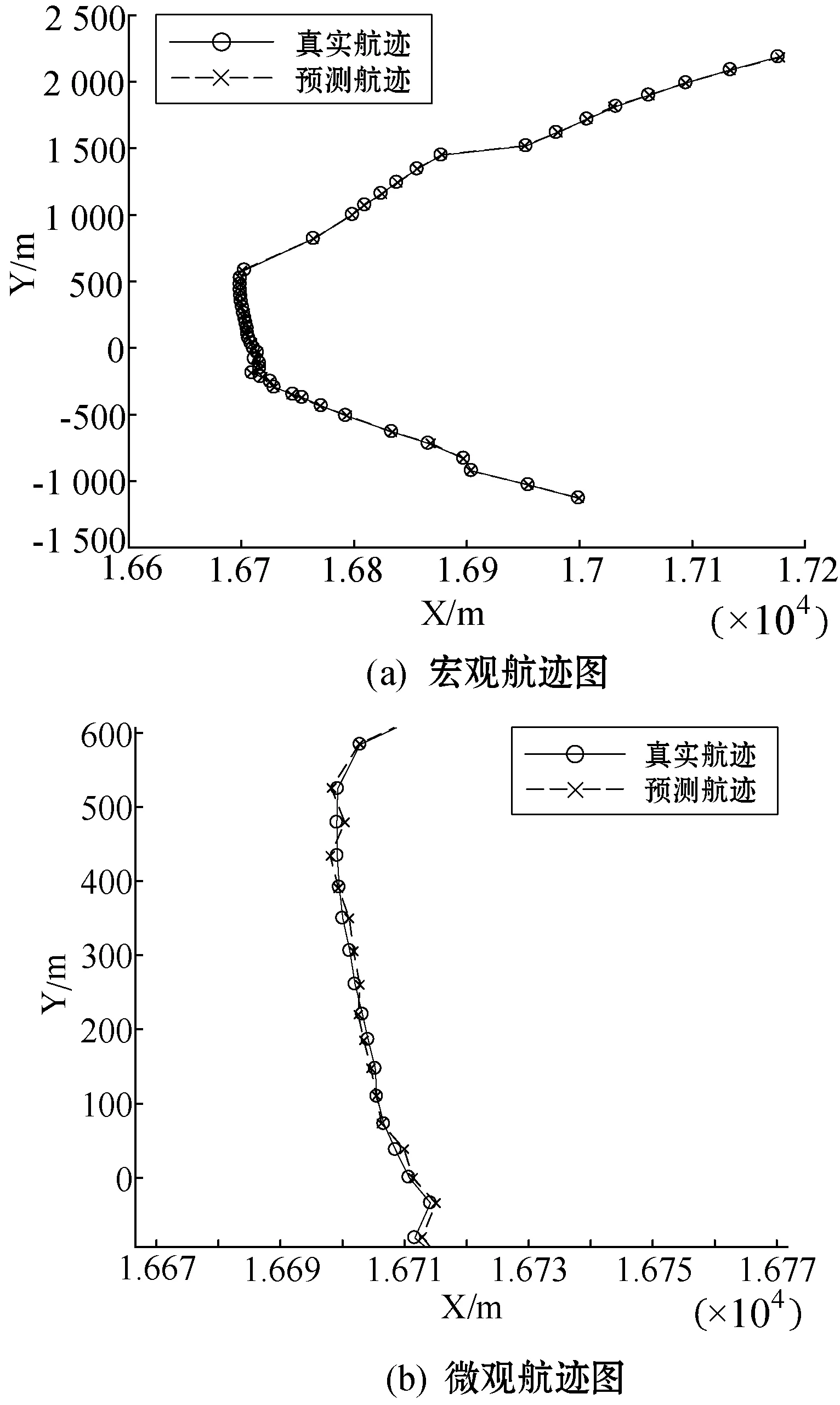
图4 航迹图

3.2 预测准确性比较

实验采用均方误差(Mean Squared Error,MSE)和平均绝对误差(Mean Absolute Deviation,MAD)比较LSTM模型和TK模型的预测精度。

均方误差反映预测精度情况，计算式表示为：

(26)

平均绝对误差反映预测值误差实际情况，计算式表示为：

(27)

式中：n为样本数量;m为量测值;p为预测值。

LSTM模型和TK模型的MSE和MAD预测误差统计情况，如表1所示。对比两种评估指标情况，虽然二者的误差处于同一量级，但TK模型的误差相对较小，预测精度更高一些，从而也能看出Transformer模型的特征提取能力和Kalman滤波的修正能力得到很好的表现。

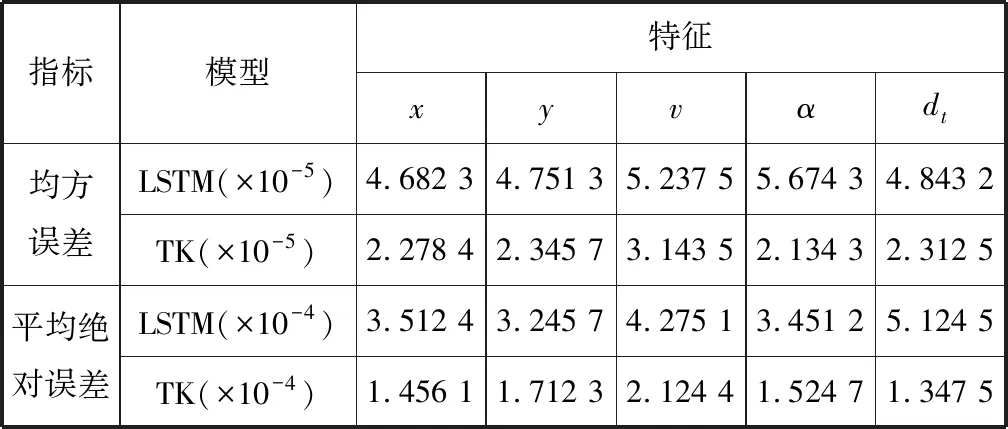
表1 LSTM模型和TK模型的均方误差和平均绝对误差

为了更好地比较模型预测精度，运用定量分析法测试各算法的预测误差、预测准确率。利用训练好的模型，针对样本单一特征数据(如横坐标位置x)，对LSTM模型、Kalman模型、多项式Kalman滤波模型、Transformer模型和TK模型预测情况进行比较，结果如图5、图6所示。

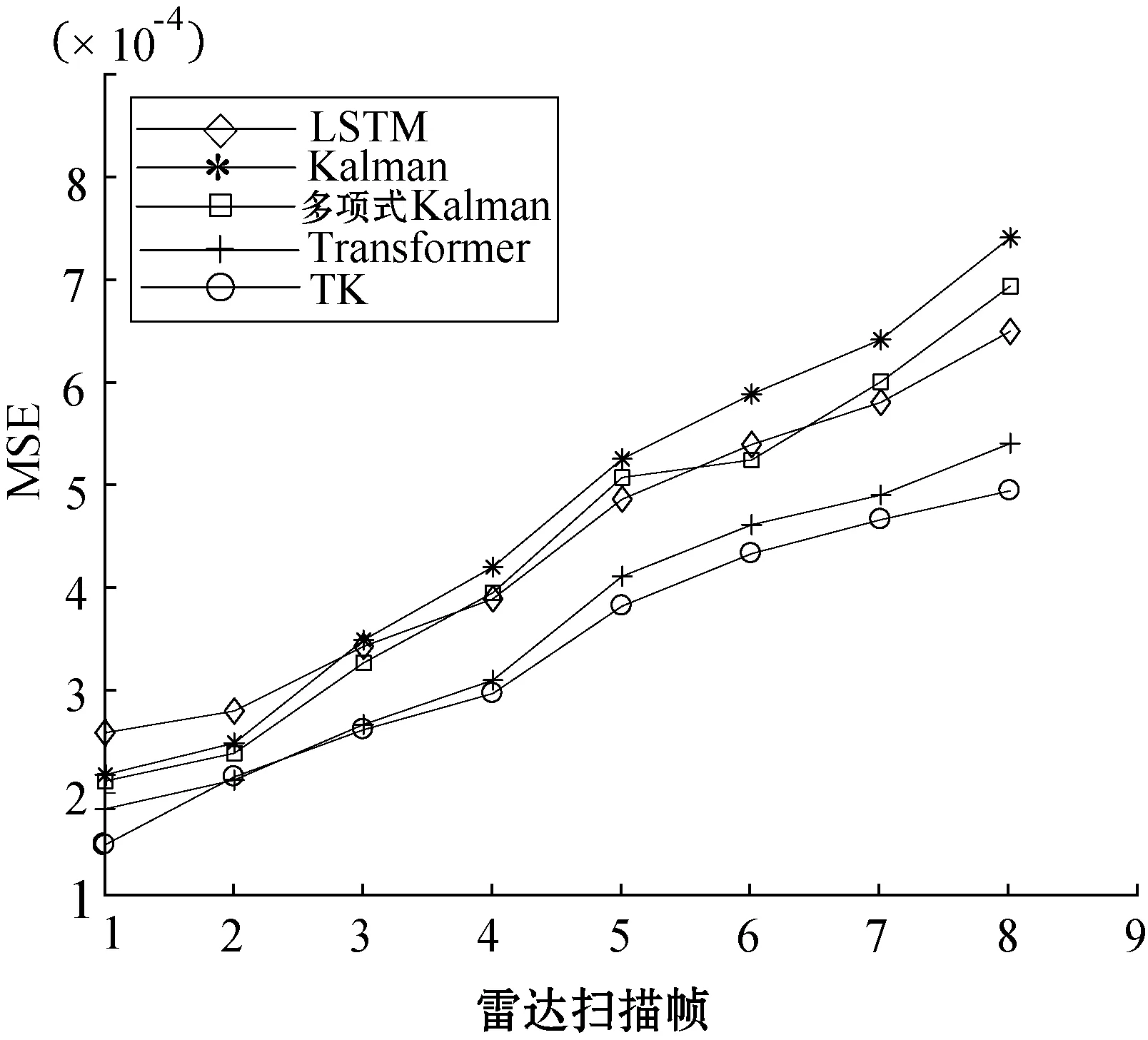
图5 均方误差对比

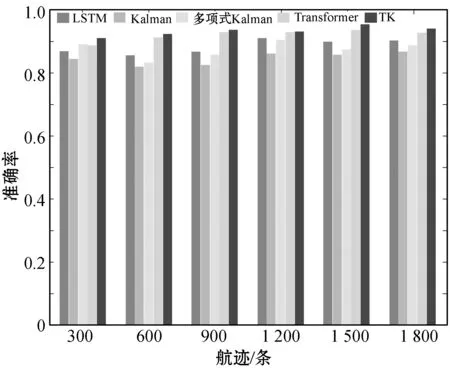
图6 准确率对比

图5连续递归测试8帧(8个时刻)，观察其均方误差变化趋势。从曲线趋势同样可以看出TK模型的均方误差小于其他几个模型，而且随着时序的积累TK模型误差曲线趋于平稳，另外四个模型的曲线趋势陡峭，表明TK模型的均方误差更加稳定。图6分别对不同数量的航迹进行训练预测比较各模型的准确率，TK模型准确率在92%左右浮动，明显高于其他几个模型。

3.3 预测时间比较

利用预测效率比较LSTM模型和TK模型二者训练模型、预测目标的时间性能，如图7所示。LSTM模型无论是训练模型还是在线预测，其运行时间相对于TK模型的时间占比大概在3～5倍之间。对于相同长度的样本，LSTM模型因为序列依赖，并行运算时无法消除样本长度，而Transformer模型却利用自注意力机制和前馈神经网络结构，很好实现并行计算能力。

预测效率定义为：

(28)

式中：tTK、tLSTM分别表示TK模型和LSTM模型的运行时间。

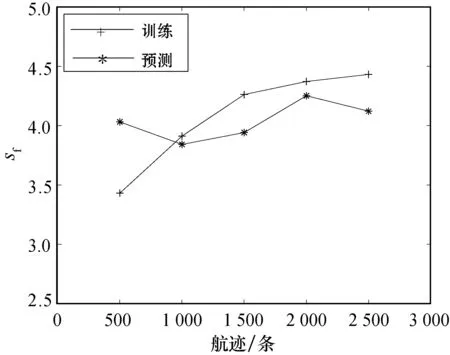
图7 运行时间

4 结 语

本文提出基于Transformer模型和Kalman滤波器的航迹预测方法。采取自注意力机制和前馈神经网络框架结构的Transformer模型，抛弃了传统的神经网络思想，利用自注意力机制提取航迹数据特征，学习航迹规律，解决了长期依赖问题；同时利用Kalman滤波器结合量测数据对预测值进行实时修正，从而获取最佳估计值。实验比较了LSTM模型、TK模型和Kalman模型的误差、准确率、时间性能。结果表明，基于Transformer模型和Kalman滤波器对航迹预测的算法具有良好的并行特性，并且特征提取能力相对LSTM模型也有较高的提升，使得预测的准确性、实时性都有良好的表现。