从频数分布图表中巧读信息
王云峰
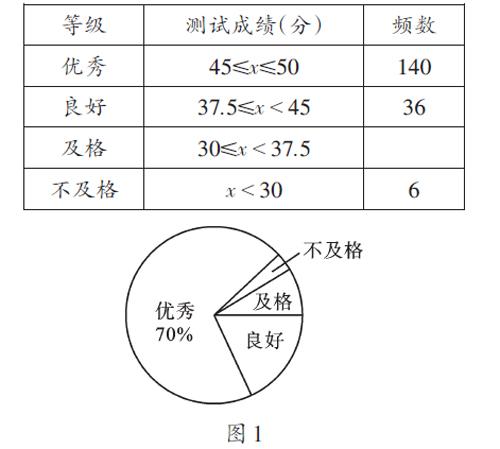


一、频数分布表与扇形统计图结合
例1 某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初学校随机选取部分学生进行体质健康测试。以下是根据测试成绩绘制的部分统计图表:
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;(2)求体质健康成绩属于“不及格”等级的频率;(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数。
【解析】在频数分布表及扇形统计图中,一般抓住所有量都已知的某个小组,利用“百分比=频数÷总数”求出总数。(1)由扇形统计图知,“优秀”等级占测试学生的70%,由频数分布表知,“优秀”等级的频数是140,据此可求出测试学生的总人数;再根据“各小组频数之和等于总数”求出“及格”等级的频数;(2)用“不及格”等级的频数÷测试学生的总人数即可求解;(3)利用“样本估计总体”的数学思想求解,即先由频数分布表中“优秀”与“良好”等级的人数之和÷测试学生的总人数,求得样本中达到“良好”及以上等级的频率,再用该频率乘总体中的学生总人数。
參考答案:(1)200(人);18。(2)0.03。(3)1584(人)。答略。
二、频数分布直方图
例2 小明统计了同学们2月份平均每天观看“空中课堂”的时间,并绘制了如图所示的频数分布直方图,得出如下结论:①一共调查了100名学生;②平均每天观看时间不足30分钟的人数占总人数的10%;③平均每天观看时间超过60分钟的人数超过调查总人数的一半;④平均每天观看时间不足60分钟的人数少于平均每天观看时间在60~90分钟的人数。其中,正确的结论是()。
A.①② B.①④
C.③④ D.②③④
【解析】解答关于频数分布直方图的多结论判断题,一般要先抓住频数分布直方图,得出各小组的频数。由频数分布直方图可知,从左到右各小组的频数分别为10,30,60,20,所以一共调查的学生数为10+30+60+20=120(名),故①不正确;平均每天观看时间不足30分钟的人数占总人数的百分比为[10120]×100%≈8.33%,故②不正确;平均每天观看时间超过60分钟的学生数为60+20=80(名),而80>[12]×120,即超过调查总人数的一半,故③正确;平均每天观看时间不足60分钟的学生数为10+30=40(名),平均每天观看时间在60~90分钟的人数为60人,而40<60,故④正确。故选C。
三、频数分布表与频数分布直方图结合
例3 为了解某校七年级学生的身高情况,在七年级每班随机抽取部分学生的身高进行调查,利用所得数据绘成如下频数分布表:
(1)求这次被调查的学生共有多少人;(2)求表中a、m的值,并补全频数分布直方图;(3)该校七年级共有800名学生,估计身高不低于160cm的学生大约有多少人。
【解析】(1)根据“百分比=[频数总数]”,不妨取频数分布表中“x<150”小组的频数6与百分比10%,即可求出总数;(2)根据“各小组频数之和等于总数”求出a的值,进而可补全频数分布直方图;利用“百分比=[频数总数]”,求出“160≤x<165”小组的百分比,进而得到m的值;(3)利用“样本估计总体”的数学思想求解,即先由频数分布表求出样本中身高不低于160cm的学生的百分比,再乘学生总数。
参考答案:(1)60(人);(2)a=9,m=35,补全频数分布直方图如图4所示。(3)360(人)。答略。
(作者单位:江苏省盐城市葛武初级中学)

