Insight into the chemomechanical coupling mechanism of kinesin molecular motors
Ping Xie
Key Laboratory of Soft Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
Abstract Kinesin is a two-headed biological molecular motor that can walk processively on microtubule via consumption of ATP molecules.The central issue for the molecular motor is how the chemical energy released from ATP hydrolysis is converted to the kinetic energy of the mechanical motion,namely the mechanism of chemomechanical coupling.To address the issue,diverse experimental methods have been employed and a lot of models have been proposed.This review focuses on the proposed models as well as the qualitative and quantitative comparisons between the results derived from the models and those from the structural,biochemical and single-molecule experimental studies.
Keywords: molecular motor,kinesin,dynamics,mechanochemistry,mechanism,catch bond
1.Introduction
Motor proteins or biomolecular motors are a group of macromolecules that typically consume the energy of a chemical reaction and convert it into mechanical motion or work to perform a myriad of biological functions in cells [1,2].A large number of molecular motors can move processively on their linear tracks[3].A typical class in this category is that of kinesin proteins,which can move processively on microtubule (MT) filaments towards the plus end by hydrolyzing ATP molecules,responsible for intracellular transport,chromosome segregation during mitosis,regulation of MT dynamics and so on[4-7].Kinesin proteins constitute a large superfamily,which can be divided into 15 families,consisting of kinesin-1 through kinesin-14 families and ungrouped family called orphan kinesin [8].Members of kinesin-1 through kinesin-12 and orphan families have their motor domains (also called heads) in the N-terminus of the polypeptide,members of kinesin-13 family have their heads in the middle of the polypeptide while member of kinesin-14 family have their heads in the C-terminus of the polypeptide.In this review,we focus mainly on the N-terminal kinesin-1,also called conventional kinesin (unless otherwise pointed out,throughout kinesin refers to kinesin-1) [4-8].Since it was discovered in 1985[9],kinesin-1 has attracted much attention and has been studied in great details because of its simple structure and function [10-14].It was considered as a model system for studying the chemomechanical coupling mechanism of the N-terminal kinesin motors.
A kinesin molecule is composed of two identical heads that are connected together by a long coiled-coil stalk through their unstructured,flexible neck linkers(NLs)[15].Each head has the ATPase activity and can bind to MT with nucleotidedependent binding energy.Upon binding to MT,the kinesin dimer advances stepwise along an MT filament in increments of about 8.2 nm,the periodicity of an MT filament,in a handover-hand manner [16,17]: a given head being displaced in discrete steps with a size of about 16.4 nm[17].With various experimental techniques,diverse aspects of the motor dynamics such as velocity,forward-to-backward stepping ratio,dwell time between two successive mechanical steps,run length,etc,as well as the dependences of these quantities on the external load in both the forward and backward directions have been well examined [16,18-26].To understand the mechanism of the chemomechanical coupling of the motor and to explain the experimental data on the motor dynamics,a lot of models have been proposed [27-34].In general,the models can be grouped into two classes(see,e.g.review paper [34]).The first and prevailing class is that the forward stepping of the motor is driven mainly by a large conformational change of the NL (termed as NL docking)induced by ATP binding [27-31],namely the forward stepping is mainly via the power-stroke(PS)mechanism,and thus this class is called NL-docking model(or PS model)here.The other one is that the forward stepping of the motor is mainly via the Brownian ratchet (BR) mechanism,and thus it is called BR model here.The preliminary form of the BR model was presented more than a decade ago(see,e.g.[34],where it was termed as two-heads-interacting plus NL-docking (THINLD) model),which was recently improved and studied in great detail [3,35-40].Here,I review the two classes of the models and particularly the BR model as well as the numerical and theoretical studies of the kinesin dynamics on the basis of the BR model.
2.NL-docking model
The critical element for the NL-docking model is the pronounced conformational change of the NL of the kinesin head[41-43].When the head is in ADP or nucleotide-free (φ)state,its NL is mobile.After ATP binding to the head,its NL becomes immobilized and extended towards the MT plus end(called NL docking).Another main element is the nucleotidedependent interaction between the head and MT[14,44-46].The head inφ,ATP or ADP.Pi state has a high affinity (ES)for MT,while in ADP state has a low affinity (Ew2).
Although there are several kinds of minor variations in this class of the models,the chemomechanical coupling pathway can be generally illustrated in figure 1.Let the pathway begin with the rear head in ATP state binding strongly to binding site I on an MT filament and the front head inφstate binding strongly to site II (figure 1(a)).The internal strain on the NLs enhances the rate of ATP hydrolysis and Pi release of the rear head that is pulled forward and inhibits ATP binding to the front head that is pulled backward.After ATP hydrolysis and Pi release in the rear head,the head in ADP state becomes binding weakly to site I,reducing the internal strain (figure 1(b)).ADP is inhibited to release from the rear head that is pulled forward although the internal strain is reduced.However,due to the reduced internal strain,ATP can bind to the front head,inducing NL docking,which drives the rear ADP-head to detach from site I and delivers the detached ADP-head to the front position(figure 1(c)).(An alternative argument is that after ATP hydrolysis and Pi release the ADP-head detaches from the rear site I and then stays at the rear position with neither rebinding to site I nor diffusing past the MT-bound head,which is impossible to realize due to the flexibility of NLs connecting the two heads and the large fluctuation of the detached head as a Brownian particle with a radius of only about 2.5 nm.The ensuing NL docking of the front head induced by ATP binding delivers the detached head to the front position).After moved to the front position,the ADPhead then binds to the nearest site III via diffusional searching,which is followed by ADP release from the head that is pulled backward (figure 1(d)).From figures 1(a) to (d),a forward step of size d = 8.2 nm was made by hydrolyzing an ATP.
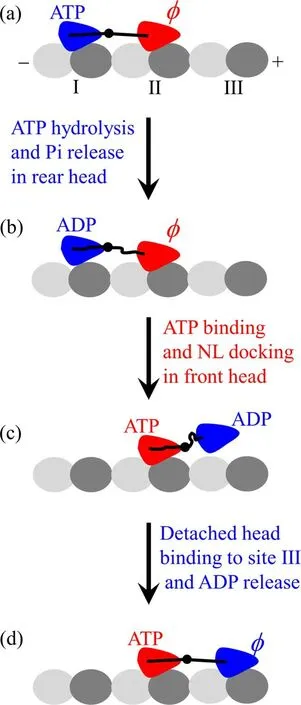
Figure 1.Schematic illustrations of NL-docking model.(a)-(d) The chemomechanical coupling pathway (see text for detailed description).Symbolφ represents nucleotide free.
The pathway dictates that the ATPase cycle is tightly coupled to the stepping cycle (abbreviated as tight chemomechanical coupling) such that every ATP molecule leads to a forward step of size d = 8.2 nm under the backward load smaller than the stall force of about(6-8)pN.It is evident that the model requires that the length of the NL should not be too long.For example,kinesin-1 head has an NL of 14 residues[15],kinesin-2 head has an NL of 17 residues [47],and kinesin-5 head has an NL of 18 residues [48].However,the N-terminal head of an orphan kinesin-phragmoplast-associated kinesin-related protein 2(PAKRP2)-has an NL of 32 residues,and the experimental data showed convincingly that PAKRP2 homodimer can also step processively on MT in the hand-over-hand manner,also with one forward step of size d = 8.2 nm by hydrolyzing one ATP molecule under no load[49].These indicate that a model rather than the NL-docking model is required for the kinesin(at least for PAKRP2)dimer.
The pathway dictates that that the kinesin dimer can only move in the direction along that of NL docking,namely in the plus-end direction,under no or low load.Surprisingly,some kinesin-5 motors such as Saccharomyces cerevisiae Cin8 and Kip1 and Schizosaccharomyces pombe Cut7 can move processively in the direction opposite to that of NL docking,namely in the minus-end direction,under no load and at high(or near-physiological) salt conditions,although these kinesin-5 motors,like kinesin-1 motors,also have the N-terminal motor domains and after ATP binding their NLs can also dock towards the plus-end direction [50].More puzzlingly,the movement direction of these kinesin-5 motors can be switched by changing the experimental conditions(e.g.at low slat,in clusters of the motors,in multi-motor MT-gliding,and in antiparallel MT sliding)under no load[50].These indicate that the NL docking is not a key determinant for the directionality of the kinesin motor,which is contradictory to the NL-docking model.
A puzzling issue for the NL-docking model,which was often mentioned in the literature [13,34,51],is that the experimentally measured free energy change associated with the NL docking of kinesin-1 is only about 1kBT[52],which is much smaller than the work done for the motor to move a step of 8.2 nm under a load of (6-8) pN,with the work estimated to be about (49-66) pN nm ≈(12-16)kBT.
Another puzzling issue similar to the above one is that by completely nullifying the NL docking via deletion of head’s strandβ0 that is essential for the NL docking the kinesin dimer can still move processively towards the plus end of MT with a large velocity close to the wild-type(WT)case under a small load and with a stall force (~2.5 pN) smaller than the WT case(~6 pN)[24].These experimental results imply that the NL docking does not play a critical role and plays only an assisting role in the kinesin motility.On the contrary,in the model the NL docking provides the driving force,i.e.plays the critical role,in the forward movement of the kinesin,and thus without the driving force the motor cannot move forward or can at most move with a very low velocity even under no load.
A confusing issue for the model is stated as follows.In order to keep the coordination between the ATPase activities of the two heads such that the tight chemomechanical coupling is maintained at low ATP concentrations [19],it was postulated that ADP is inhibited to release from the rear head.On the contrary,in order to explain the ATP-dependent backward stepping (noting that even under no load the backward stepping can occur)[25],it was assumed that ADP can be released from the rear head [53,54].However,with the latter assumption,multiple ATP molecules are expected to hydrolyze per forward step at a very low ATP concentration even under no load,which is contrary to the experimental data[19].Moreover,the latter assumption conflicts with the biochemical data showing that upon the kinesin dimer with both heads bound by ADP mixing with MT in solution in the absence of ATP only half fraction of ADP molecules are released [55].
Additionally,as showed elsewhere [3],based on the model,which dictates the tight chemomechanical coupling under the backward load smaller than the stall force,the following issues are contrary to the experimental data.To theoretically reproduce the experimentally measured loadvelocity curve,the ATPase rate is required to change greatly with the change of the load on the stalk,which is contrary to the experimental evidence that reducing greatly the strain on the NL by extending the NL has nearly no effect on the ATPase rate of the motor but affects significantly its velocity[56].Since for the dimer with two heads bound to MT the internal force on its NLs is more than 25 pN [26,35] and for the monomer no internal force is presented,it is expected that under no external force the rate of ATP hydrolysis and Pi release of the truncated monomer should be significantly different from that of the dimer.This is inconsistent with the available experimental data showing that the rate of ATP hydrolysis and Pi release of the truncated monomer is nearly equal to that of the dimer [30,57,58].Under a medium backward load on the stalk (e.g.3 or 4 pN),the theoretical results predict that the dwell-time distribution for the forward steps has evidently a two-exponential form,which is contrary to the available single-molecule data showing that the dwelltime distribution is single exponential [21,23].While the dependence of ATPase rate upon load acting on the stalk can be explained by the load-dependent effect of NL on its head[59],for the case of load on one head via an external linker,since the external linker has no such effect on the head,it is puzzling how the load affects more sensitively the ATPase rate and thus the velocity [60].Moreover,based on the pathway (figure 1) it is expected that the presence of added salt in the buffer,which would reduce the binding energy between the head and MT,would have the same effect on the reduction of the run length under loads in both the forward and backward directions.However,the available experimental data showed that the presence of added salt reduces greatly the run length under a 4 pN backward load whereas has a small effect under a 4 pN forward load [61].
3.BR model
3.1.Three elements in the BR model
The BR model is constructed mainly on the basis of following three elements that are consistent with the experimental,structural and atomistic molecular dynamics(MD)simulation evidence.
3.1.1.Interaction between kinesin head and MT.A head inφ,ATP or ADP.Pi state has a strong interaction with an MTtubulin,while in ADP state has a weak interaction [14,44-46].The strong interaction induces large conformational changes of the MT-tubulin [62] and the weak interaction induces little conformational changes [39].After the MTbound head releases Pi,the head has temporarily a much weaker binding energy(Ew1)to the local MT-tubulin with the large conformational changes than the weak binding energy(Ew2) to other MT-tubulins without the conformational changes,as atomistic MD simulation indicated [39].Then,the local MT-tubulin restores elastically(with a time period trof the order ofμs) to its normally unchanged conformation,with the binding energy of the ADP-head to the local MTtubulin changing from Ew1to Ew2.
3.1.2.Conformational change and NL docking.A head inφor ADP state has the conformation that its NL docking is unable to occur[41-43].When the MT-bound head is in ATP or ADP.Pi state a large conformational change can take place[63,64],enabling the NL docking to occur [41-43].
3.1.3.Interaction between two heads.The MT-bound head without the large conformational change has a high binding energy with the other detached ADP-head while with the large conformational change has a much lower binding energy,as atomistic MD simulation indicated [40].
The detailed correlations among the large conformational change of the head in ATP or ADP.Pi state,weakening its affinity with the detached ADP-head and its NL docking are described in appendix.As showed elsewhere[40],the relative position and orientation of the detached ADP-head to the head bound strongly to MT,which were determined using atomistic MD simulation for element(iii),are consistent with the cryo-EM image observed by Alonso et al [65] and the single-molecule FRET data of Mori et al [66].Based on elements(ii)and(iii),the biochemical data showing that upon the kinesin dimer with both heads bound by ADP mixing with MT only half fraction of ADPs were released and the addition of ATPs led to the release of the other half fraction of ADPs[55] can be understood easily.As discussed elsewhere [40],element(iii)can also explain the single-molecule microscopic imaging observations by Isojima et al [67] and the singlemolecule optical trapping data of Guydosh and Block[60]on the position of the detached ADP-head relative to the MTbound head in intermediate(INT)state.In particular,element(iii) explained well the experimental data for orphan kinesin PAKRP2 showing that although the dimer walked in the hand-over-hand manner with the step size of about 8.2 nm by hydrolyzing one ATP under no load,the step-size distribution of a given head showed the sizes around 8.2 nm,rather than around 16.4 nm,constituting the dominant fraction [49,68].
3.2.The chemomechanical coupling pathway
The chemomechanical coupling pathway at saturating ATP is illustrated schematically in figure 2.ATP can bind to both rear and front heads,but with the rate constant of ATP release from the front head being larger or much larger than that from the rear head (see appendix).Since at saturating ATP after ATP or ADP release from one head an ATP can bind immediately,the lifetime ofφstate is so short that theφstate is neglected here.Let the pathway begin with two heads in ATP state binding strongly to binding sites II and III on an MT filament,with the rear head having closed nucleotidebinding pocket (NBP) and the large conformational change while the front head,due to the NL interference,having open NBP and without the large conformational change (see appendix) (figure 2(a)).The rear head has a much larger rate of ATP hydrolysis and Pi release than the front head(see next section).
First,consider ATP hydrolysis and Pi release taking place in the rear head,inducing the reverse large conformational change and NBP opening of the head in ADP state.Facilitated by the large stretched force on the NL [35],the rear ADP-head detaches readily from site II by overcoming the small Ew1and diffuses rapidly to INT position relative to the MT-bound head,where the two heads have the high affinity(figure 2(b)).In other words,due to the large stretched force on the NL and small Ew1,site II can be considered as the‘reflecting’ boundary,while due to the high affinity between the two heads,INT position can be considered as the‘absorbing’ boundary,making the ADP-head diffuse from site II to INT position within time tr.In INT state,without the NL interference the NBP closing and large conformational change of the MT-bound ATP-head take place (see appendix),reducing greatly its affinity to the ADP-head and enabling its NL docking (figure 2(c)).The detached ADPhead can then either(with probability PE)diffuse forward and bind to site IV with affinity Ew2by stretching NLs(figure 2(d))or(with probability 1-PE)diffuse backward and bind to site II with affinity Ew2by undocking the NL,inducing the reverse large conformational change and NBP opening of the front ATP-head due to the NL interference,and stretching NLs.The small energy barriers arising from undocking NL and making the reverse large conformational change of the MT-bound head give PEclose to one under no or a small backward load but evidently smaller than one under a medium or large backward load.After the ADP-head binding to MT,ADP is released,followed immediately by ATP binding,and then the rear ATP-head closes its NBP and makes the large conformational change(figure 2(a))while the front ATP-head,due to the NL interference,cannot make the large conformational change and its NBP is kept in the open form (figure 2(e)).From figures 2(a) to (c) to (e),the dimer moved forward by a step of size d = 8.2 nm by hydrolyzing an ATP.From figures 2(a) to (c) and then returning to 2(a),the dimer did not move although an ATP was hydrolyzed.
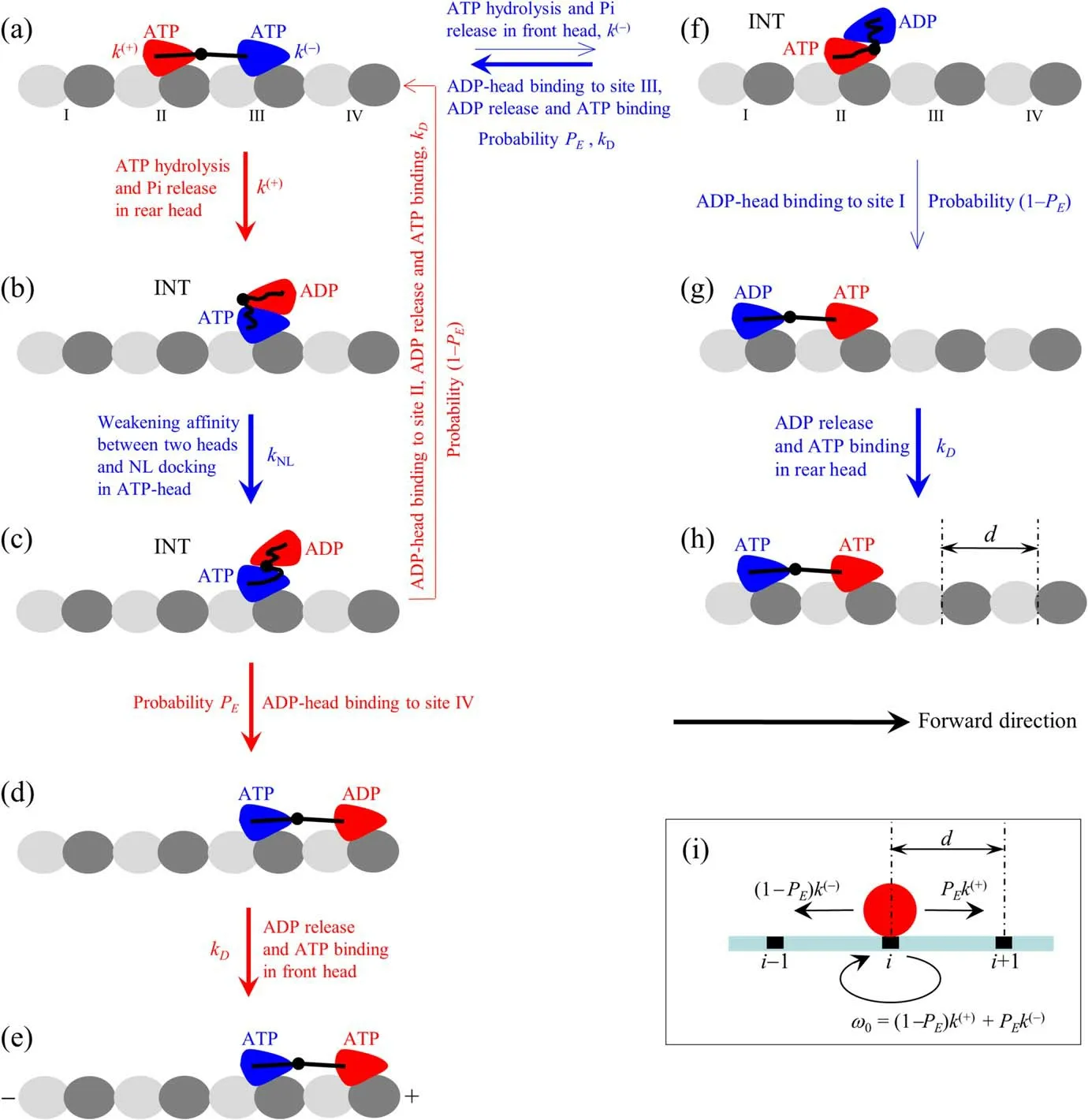
Figure 2.Schematic illustrations of BR model.(a)-(h) The chemomechanical coupling pathway at saturating ATP (see text for detailed description).The thickness of the arrow represents the magnitude of the transition probability under no load.Since in both ATP and ADP.Pi state the head binds strongly to MT,for simplicity,ATP hydrolysis and Pi release are drawn here as one step,with symbol ATP representing both ATP and ADP.Pi states and the transition from ATP to ADP consisting of two sequential transitions of ATP to ADP.Pi and of ADP.Pi to ADP.(i) The simplified model derived from the pathway shown in (a)-(h).The red circle represents the center of mass of the dimer.The positions of binding sites on the MT filament are denoted by…,(i - 1),i,(i + 1),….The motor can step forward and backward with rates PEk(+) and (1 - PE)k(-),respectively,where PE is effective chemomechanical coupling probability,and k(+) and k(-) are rates of ATP hydrolysis and Pi release of the rear and front heads,respectively.
Second,consider ATP hydrolysis and Pi release taking place occasionally in the front head in figure 2(a).Facilitated by the large stretched force on the NL,the front ADP-head detaches readily from site III by overcoming the small Ew1and diffuses to INT position(figure 2(f)).The detached ADPhead can either (with probability PE) diffuse forward and rebind to site III with affinity Ew2in time trby stretching NLs or(with probability 1-PE) diffuse backward and bind to site I with affinity Ew2by undocking the NL,inducing the reverse large conformational change of the front ATP-head and stretching NLs(figure 2(g)).After ADP-head binding to MT,ADP is released,followed immediately by ATP binding(figure 2(a)or(h)).From figures 2(a)to(f)and then returning to 2(a),the dimer did not move by hydrolyzing an ATP.From figures 2(a)to(f)to(h),the dimer moved backward by a step of size d = 8.2 nm by hydrolyzing an ATP.
3.3.Force-independent but NL-orientation-dependent rate of ATP hydrolysis and Pi release
To be consistent with the experimental evidence that the extension of the NL of each head has little effect on the ATPase rate of the kinesin dimer during its processive movement on MT [56],it was proposed that the rate of ATP hydrolysis and Pi release(the rate-limiting step of the ATPase activity)of the kinesin head is independent of the force on its NL [35-38].However,the orientation of the NL has a large effect: the head with the forward NL orientation having a much higher rate of ATP hydrolysis and Pi release than the head without the forward NL orientation[35-38].This can be understood as follows.Without the effect of the interaction with NL in the forward orientation the head has a very low rate of ATP hydrolysis and Pi release,and the interaction of the NL in the forward orientation with the head enhances greatly the rate of ATP hydrolysis and Pi release.This is consistent with the experimental evidence that deleting NL in the kinesin head or reducing the interaction of NL with the head by mutations reduces greatly the ATPase rate while has no effect on the ADP release rate [69],because after ATP binding and before Pi release the docked NL is in the forward orientation.It should be mentioned that since an ATP hydrolysis provides a free-energy change of as large as about 20kBT,for a good approximation,the reverse chemical reactions are not needed to consider.
3.4.Numerical results reproducing experimental data
Based on the BR model (figure 2),the Langevin equations can be written for the mechanical stepping following Pi release in one head,including those for the translation motion of the ADP-head in three dimensions and those for the rotation motion of the ADP-head in three directions relative to the other head bound to MT[35,36,68,70-73].The flexible NL was considered to have no compressional rigidity and the internally stretching force on the NL were determined using atomistic MD simulations [35,36,68,70-73].The Langevin equations can be solved numerically with stochastic Runge-Kutta algorithm.By also considering continuous ATPase activities of the two heads,which can be simulated with Monte-Carlo algorithm,the motion trajectory of the kinesin dimer can be obtained [35,36,68,70-73].From a lot of simulated trajectories,the motor’s mean velocity,stepping ratio,dissociation rate,run length,randomness parameter,chemomechanical coupling efficiency (i.e.the inverse of mean number of ATP molecules consumed per mechanical step),etc,and the distributions of velocities and run lengths can be calculated statistically.
The calculated results [35,36,72] reproduced quantitatively the experimental data on diverse aspects of the kinesin dynamics such as the dependences of stepping ratio,velocity,dissociation rate,run length,randomness parameter,chemomechanical coupling ratio,etc,upon the load acting on the stalk and upon the load acting on one of the two heads for the wild-type kinesin,the mutant one with nullification of its NL docking and the mutant one with extension of its NLs.In particular,the calculated results [36] explained well the dramatic asymmetry of the run length with respect to the direction of the external load acting on the stalk,with the run length under a small forward load being an order of magnitude shorter than that under the corresponding backward load[26].The calculated results[72]explained well the slip-catchslip bond behavior for the dissociation rate of the dimer during its processive motion under the backward load: with the increase of the backward load,the dissociation rate firstly increasing exponentially,then decreasing and then increasing again [74].The experimental data on the asymmetric or limping dynamics of kinesin homodimers were also reproduced quantitatively [70].Moreover,the rather different features on the load dependence of the run length for three families of kinesin dimers-kinesin-1,kinesin-2 and truncated kinesin-5 Eg5-were explained quantitatively[71].The approximate Gaussian distribution of run lengths for cargoinduced dimerized kinesin-3 compared with the singleexponential distribution of run lengths for kinesin-1 as well as the peculiar feature of the load dependence of dissociation rate for kinesin-3 dimer were explained well [73].More interestingly,the puzzling stepping features of orphan kinesin PAKRP2 dimer,which has an NL of 32 residues in each head,compared with those of kinesin-1,which has an NL of only 14 residues in each head,were also explained well[68].
3.5.Analytical expressions for stepping ratio,stall force,velocity,dwell time and chemomechanical coupling efficiency
Here,we focus only on saturating ATP concentrations.Denote by k(+)the rate of ATP hydrolysis and Pi release of the rear head with the forward NL orientation,byis the rate of ADP release from the rear head,by k(-)the rate of ATP hydrolysis and Pi release of the front head without the forward NL orientation,and bythe rate of ADP release from the front head.For simplicity,the rate of MT-stimulated ADP release is treated here to be independent of the force on and orientation of the NL,withIn addition,denote by kNLthe rate of NL docking of the MT-bound head under no load (which is equal to the rate of reducing the affinity between the two heads) in INT state.
The experimental data showed that ADP release is a nonrate-limiting step of the ATPase activity [57] and the rate of NL docking is much larger than the rate of ATP hydrolysis and Pi release [75],implying kD≫k(+)and kNL≫k(+).Under these approximations,the pathway illustrated in figures 2(a)-(h) can be simplified to that shown in figure 2(i)[3,76] and the following expressions for the load dependences of stepping ratio r,probability PE,velocity v,dwell time Tdand number N of ATP molecules consumed per mechanical step (either forward or backward step) can be obtained [3,38,76]


Table 1.Parameter values for different species of kinesin under different experimental conditions used in BR model.
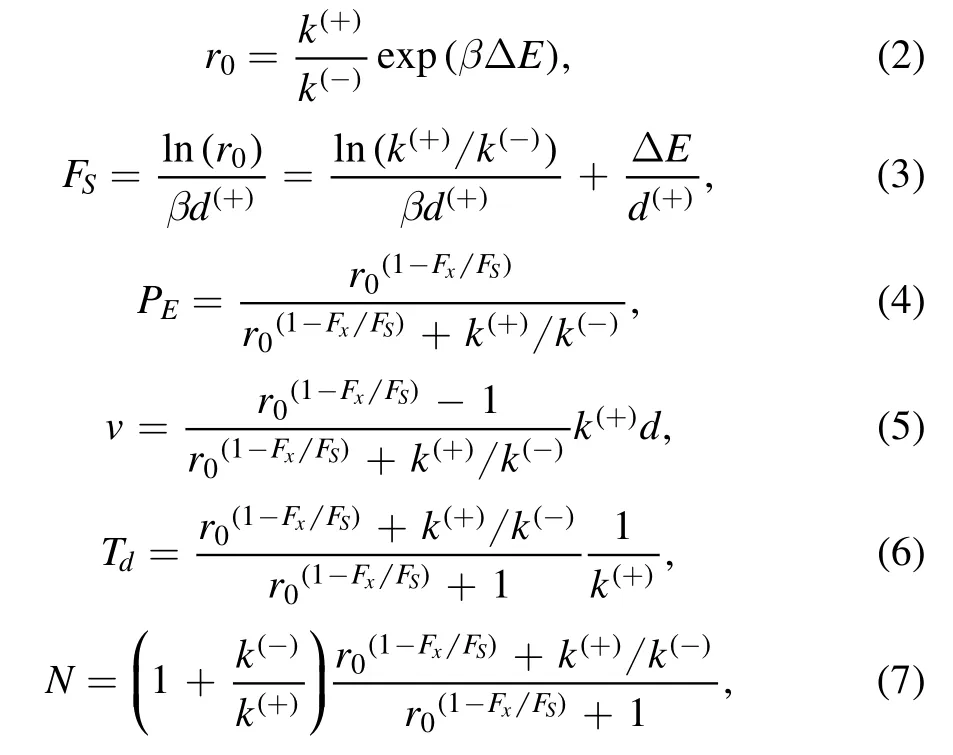
where Fxis the horizontal component of the load on the stalk,which is defined to be positive when it is in the backward direction,r0is the unloaded stepping ratio,FSis the stall force,ΔE= ΔE1+ ΔE2,withΔE1being the free energy change associated with the large conformational change of the MT-bound head in ATP or ADP.Pi state andΔE2being the free energy change associated with the NL docking,d(+)is the distance parameter for the movement of the ADP-head from INT position to the binding site on MT,andβ-1=kBT,with kBbeing the Boltzmann constant and T the absolute temperature.
Using equations (1),(5) and (6) and with only four adjustable parameters r0,FS,k(+)and k(-),each of which has a clear physical meaning (see definitions above),the experimental data on load dependences of stepping ratio,velocity and dwell time can be reproduced well[37,38].For example,with r0= 350,FS= 7.6 pN,k(+)= 128-s1and k(-)= 3-s1
(table 1) the single-molecule data for bovine brain kinesin at saturating ATP(1 mM)measured by Nishiyama et al[23]can be reproduced well (figures 3(a)-(c)); with r0= 900,FS= 7 pN,k(+)= 100-s1and k(-)= 3-s1(table 1) the singlemolecule data for Drosophila kinesin at saturating ATP(1 mM)measured by Carter and Cross[25]can be reproduced well (figures 3(d)-(f)).Note that the above k(+)= 128-s1or 100-s1for the rear head with the forward NL orientation is consistent with the biochemically determined rate of ATP transition to ADP for the truncated kinesin monomer whose docked NL after ATP binding is in the forward orientation[57].The above k(-)= 3-s1for the front head with the backward NL orientation,which is about 33-fold or 43-fold smaller than k(+),is consistent with the biochemical data showing that deleting NL in the kinesin head or reducing the interaction of NL with the head by mutations decreased the ATPase rate by about 27-60-fold while had no effect on the ADP-release rate [69],because the NL in the backward orientation has a little interaction with the head.The total rate k(+)+ k(-)= 103-s1or 131-s1is also consistent with the biochemical data for the dimer [57,77].Moreover,with the above values,from equation (2) it is calculated thatΔE= 2.1kBT for bovine brain kinesin andΔE= 3.3kBT for Drosophila kinesin.ConsideringΔE= ΔE1+ ΔE2,these small values ofΔEgive a good explanation of the experimentally measured free energy change associated with the NL docking (ΔE2) being only about 1kBT [52].WithΔE2= 1kBT,from the above values ofΔE= ΔE1+ ΔE2we have the free energy change associated with the large conformational change of the ATP- or ADP.Pi-head (ΔE1)being about 1.1kBT-2.3kBT,which is also in good agreement with the atomistic MD simulation value of about 1.7kBT [78].
Considering k(-)≪ k(+)andfrom equation (7) it is noted that under no or a small backward load,we have N ≈1 (figure 4),implying nearly tight chemomechanical coupling,which is consistent with the experimental data showing that under near-zero load kinesin hydrolyzes nearly one ATP molecule per mechanical step[79,80].However,under a large backward load,and from equation (7) we have(figure 4),implying evidently nontight chemomechanical coupling,namely a chemical reaction of ATP hydrolysis being not necessarily generating a mechanical step,which is hoped to test experimentally in future.
It is noted that equations (1)-(7) are only applicable to the case of load on the WT kinesin.The analytical expressions for the case of load on the mutant kinesin with extension of its NLs were also presented[38],where with the same four parameters r0,FS,k(+)and k(-)and only one additionally adjustable parameter for the mutant one the available singlemolecule data for both the WT and mutant motors [26,54]were reproduced consistently and quantitatively.
More interestingly,with the BR model the puzzling features for some kinesin-5 motors such as S.cerevisiae Cin8 and Kip1 and S.pombe Cut7 that can move processively in the minus-end direction at high (or near-physiological) salt conditions and switch to the plus-end direction at low saltconditions can also be explained well [81].The physical origin of why kinesin-1 motors can only make unidirectional movement and these kinesin-5 motors can make bidirectional movements under no load was revealed [81].The available experimental data about different movement directions under different experimental conditions and about mutations or deletions of several structural elements affecting the directionality of these kinesin-5 motors were explained well [81].
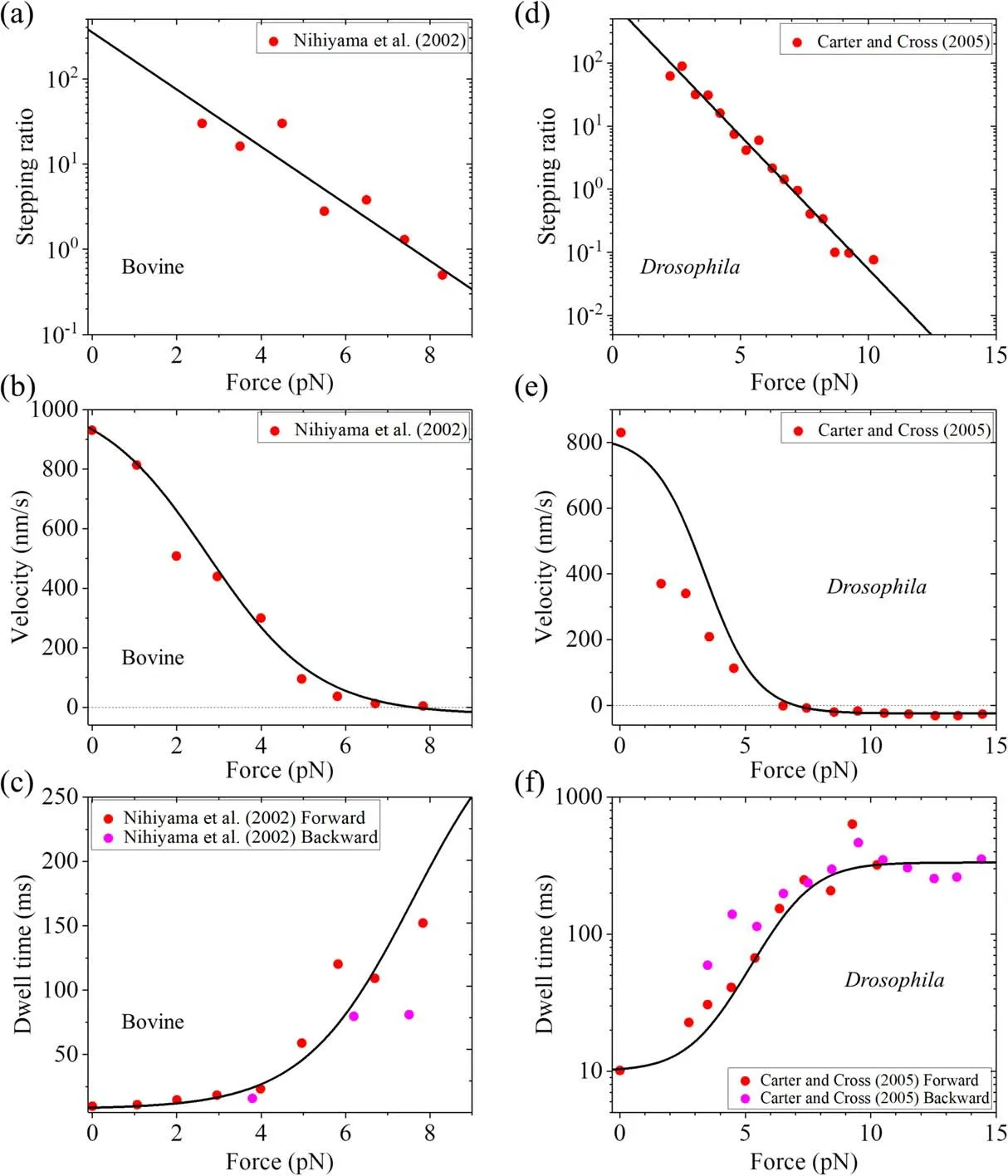
Figure 3.Comparisons between theoretical results obtained based on BR model and experimental data for different species of kinesin.Lines are theoretical results,and symbols are experimental data at saturating ATP(1 mM).Left panels(a)-(c)are for bovine brain kinesin,with the theoretical results calculated with parameter values given in table 1 and the experimental data taken from Nishiyama et al[23].Right panels(d)-(f)are for Drosophila kinesin,with the theoretical results calculated with parameter values given in table 1 under experimental condition of Carter and Cross [25] and the experimental data taken from Carter and Cross [25].(a),(d) Stepping ratio versus load.(b),(e) Velocity versus load.(c),(f) Dwell time versus load.
3.6.Analytical expressions for dissociation rate and run length
The dissociation of kinesin from MT can be studied by considering the dissociation during the period of weak MTbinding state and that of strong MT-binding state of the dimer in one chemomechanical coupling cycle,separately [76].Since the occurrence of weak MT-binding state is determined by the rate of reducing affinity between the two heads(which is equal to the rate of the NL docking of the MT-bound head under no load)in INT state and rate of ADP release relative to the rate of ATP hydrolysis and Pi release,the large rates kNLand kDmust be considered to study the dissociation.
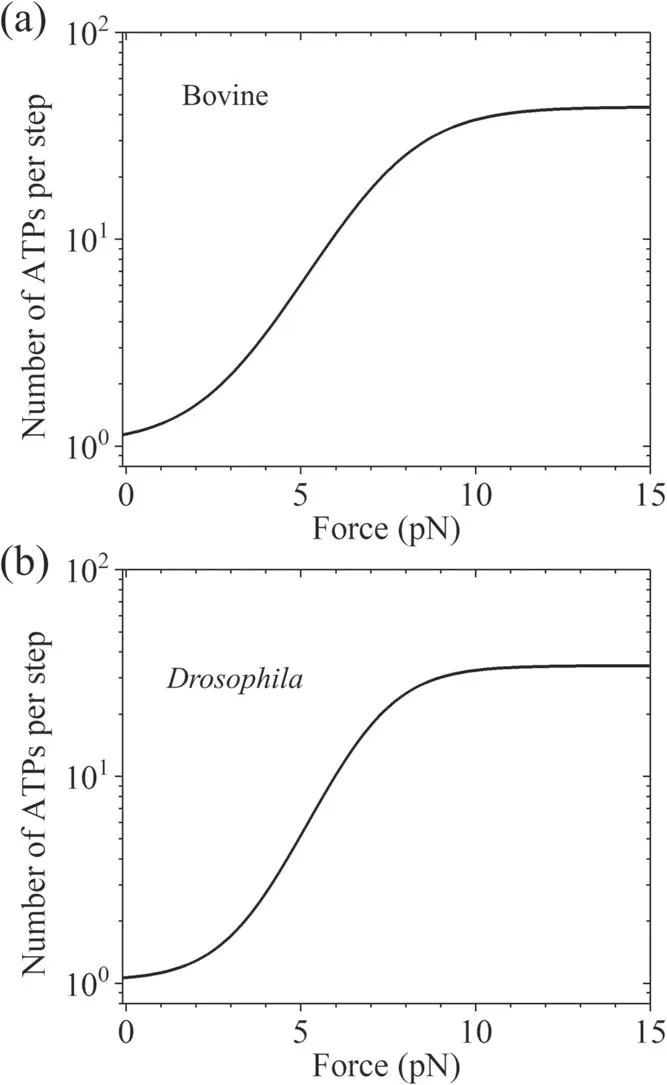
Figure 4.Theoretical results for number of ATP molecules hydrolyzed per mechanical step versus load obtained based on BR model.(a)Results calculated with parameter values given in table 1 for bovine brain kinesin.(b) Results calculated with parameter values given in table 1 for Drosophila kinesin under experimental condition of Carter and Cross [25].
From the BR model (figure 2),the weak MT-binding state can occur during two periods.One period (termed as Period I) occurs from INT state (see,e.g.figure 2(b)) when ATP in the MT-bound head transition to ADP takes place before the reduction of the affinity between the two heads[76].In Period I,one head in ADP state binds weakly to MT with affinity Ew1and the other ADP-head binds to the MTbound head with high affinity.The other period (termed as Period II) occurs from state of figure 2(d) when ATP in the rear head transition to ADP takes place before ADP release from the front head or occurs from state of figure 2(g) when ATP in the front head transition to ADP takes place before ADP release from the rear head[76].In Period II,one head in ADP state binds weakly to MT with affinity Ew2and the other ADP-head binds to the MT-bound head with high affinity.When only dissociation in periods of weak MT-binding state,including Periods I and II,is considered,the dissociation rate can be written as [76]
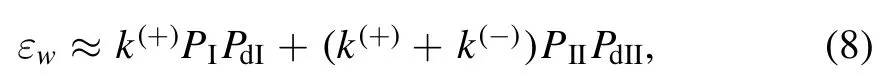
where PIis the occurrence probability of Period I in one ATPase cycle,PdIis the dissociation probability during Period I,PIIis the occurrence probability of Period II in one ATPase cycle,and PdIIis the dissociation probability during Period II.
For Period I,PIcan be calculated with [76]
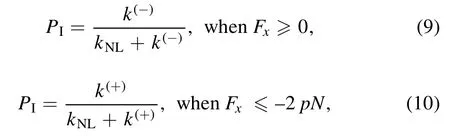
where it is considered that under no or a backward load(Fx≥0) on the stalk the NL of the MT-bound head in INT state before NL docking is not in the forward orientation,with the rate of ATP hydrolysis and Pi release equal to k(-),while under a forward load on the stalk with the magnitude of its horizontal component lager than or equal to 2 pN (Fx≤ - 2 pN)the NL of the MT-bound head in INT state before NL docking is driven to be in the forward orientation,with the rate of ATP hydrolysis and Pi release equal to k(+).Under the forward load with the magnitude of its horizontal component smaller than 2 pN,the following phenomenological form can be adopted for the rate of ATP hydrolysis and Pi release of the MT-bound head
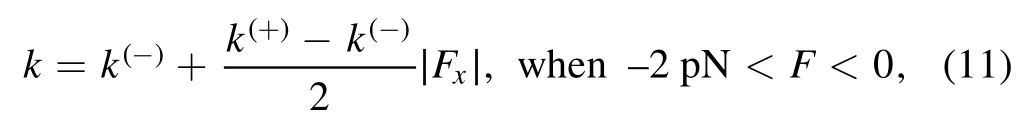
where k = k(-)when Fx= 0 and k = k(+)when Fx= -2 pN.The occurrence probability of Period I can then be calculated with
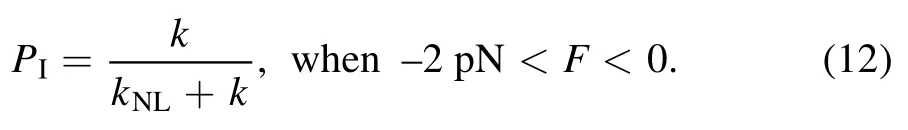
In Period I,since Ew1is very small kinesin can dissociate from MT with a nearly 100%probability even under no load,giving PdI≈1 under any load.
It is noted that during the very short-time period after the reduction of the affinity between the two heads and before the detached ADP-head binding to MT,when only one head is bound to MT,ATP transition to ADP in the MT-bound head can also take place occasionally.For simplicity,the effect of this very short-time period on probabilityPIhas not been considered in equations (9)-(12),which is a good approximation in the dilute medium with the viscosity being nearly equal to that of water,as usually used in the experiments.However,in a crowded medium with the effective viscosity being much larger than that of the water,especially under backward loads,the time of detached head diffusing from INT position to binding site on MT becomes not very short and its effect on probability PImust be considered.
For Period II,PIIand PdIIcan be calculated with [76]
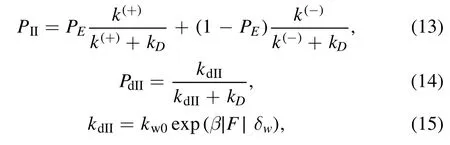
where kdIIis the dissociation rate in Period II,with kw0being the dissociation rate under no load andδwbeing the distance parameter for the weak interaction between the kinesin head and MT-tubulin.Equation (15) is consistent with Kramers theory.is the total load acting on the stalk of the kinesin,where Fxis the horizontal component,as defined above,and Fyis the vertical component.Fycan be calculated byFy= ∣Fx∣ tan Θand Θ = sin-1where RBis the radius of the bead attached to the stalk and lK= 35 nm is the stalk length.
Periods I and II can occur only occasionally in a chemomechanical coupling cycle and if occur they constitutes only a small fraction of the whole period of the chemomechanical coupling cycle,implying that during the processive motion the motor is almost always in the strong MTbinding state.Thus,according to Kramers theory,when only dissociation in period of the strong MT-binding state is considered the dissociation rate can be approximately calculated with
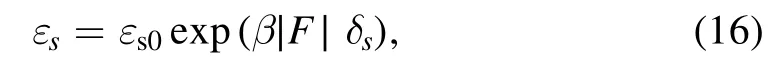
whereεs0is the dissociation rate under no load andδsis the distance parameter for the strong interaction between the kinesin and MT.
The total dissociation rate can be calculated with

The run length can then be calculated with

where v is velocity that can be calculated with equation (5).
With equations(5)and(8)-(18)the experimental data on load dependence of run length and dissociation rate can be reproduced quantitatively [76].In particular,the dramatic asymmetry of the run length with respect to the loading direction and the slip-catch-slip bond characteristic for the dissociation rate under the backward load can be explained well.For example,with parameters given in table 1,the comparisons between the theoretical and experimental data for Drosophila kinesin at saturating ATP (2 mM) are shown in figure 5.Note that in table 1 the rate of ADP release,kD= 300-s1,is consistent the biochemical data[57,77],and the rate of NL docking,kNL= 1500-s1,is also consistent with the biochemical data [75].The dramatic asymmetry of the run length with respect to the loading direction can be understood as follows.Under no or a backward load the dissociation occurring during Period II makes the main contribution to the total dissociation of the motor,while under a forward load the dissociation occurring during Period I makes the main contribution to the total dissociation.The occurrence probability of Period I under the forward load is much larger than that under the corresponding backward load,which is in turn due to that the rate of ATP hydrolysis and Pi release under the forward load is much larger than under the corresponding backward load,as seen from equations(9)and(10).The slip-catch-slip bond characteristic for the dissociation rate under the backward load arises from the cooperative effects of the backward load on the occurrence probability of Period II,on the dissociation rate in Period II and on the dissociation rate in the strong MT-binding state,as seen from equations (13)-(16).
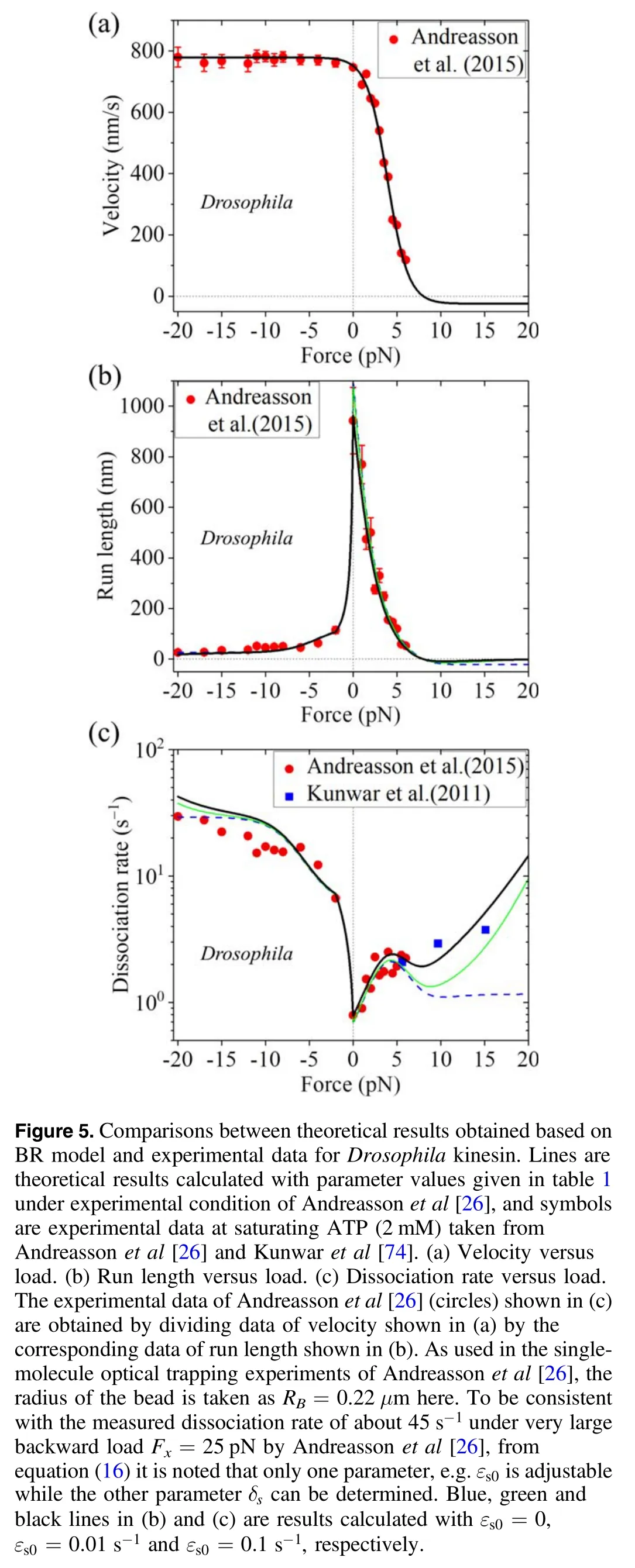
More interestingly,with equations (5) and (8)-(18) the experimental data about the effect of added Pi and that of added salt on the run length [26,61] can be explained well.First,consider the presence of added Pi.The transition of ADP.Pi to ADP can be considered to be composed of two steps.The first step is that Pi is released but the orientation of ADP in NBP and the conformation of the head have not been changed yet,with the head still having the conformation in ADP.Pi state.The second step is that the orientation of ADP in NBP is changed and thus the conformation of the head is changed,with the head having the conformation in ADP state.After Pi release and before the second step,Pi can bind to the head.After the second step,the steric restriction induced by the change in the orientation of ADP in NBP does not allow Pi to bind.Thus,the presence of added Pi elongates the lifetime of the conformation of the head in ADP.Pi state or equivalently reduces rates k(+)and k(-)in the model.In figure 6(a) we show the load dependence of the ratio of run length calculated with k(+)and k(-)being reduced by 2-fold to that with unchanged k(+)and k(-)for Drosophila kinesin.It is seen that with k(+)and k(-)being reduced the run length under the forward load is increased by more than 1.8-fold,which is consistent the experimental data showing that in the presence of added Pi the run length is increased by nearly 2-fold under a forward load of 4 pN [26,61].Second,consider the presence of added salt,which reduces the binding affinity between the head and MT or equivalently increases dissociation rates kw0andεs0in the model.In figure 6(b) we show the load dependence of the ratio of run length calculated with unchanged kw0andεs0to that with kw0andεs0being increased by 4-fold for Drosophila kinesin.It is seen that with kw0andεs0being increased the run length has a large reduction under no or a backward load whereas has a small reduction under a forward load,which explains well the puzzling experimental data showing that in the presence of added salt the run length is reduced greatly under a backward load of 4 pN whereas has a small reduction under a forward load of 4 pN [61].These results of different effects of added salt on the run length under different loading directions can be explained as follows.Under no or backward load,the dissociation occurring during Period II makes the main contribution to the total dissociation of the motor.As see in equation(15),increasing kw0increases the dissociation rate in Period II.Under the forward load,the dissociation occurring during Period I makes the main contribution to the total dissociation of the motor.As seen in equation (10),the dissociation rate in Period I is independent of kw0andεs0.
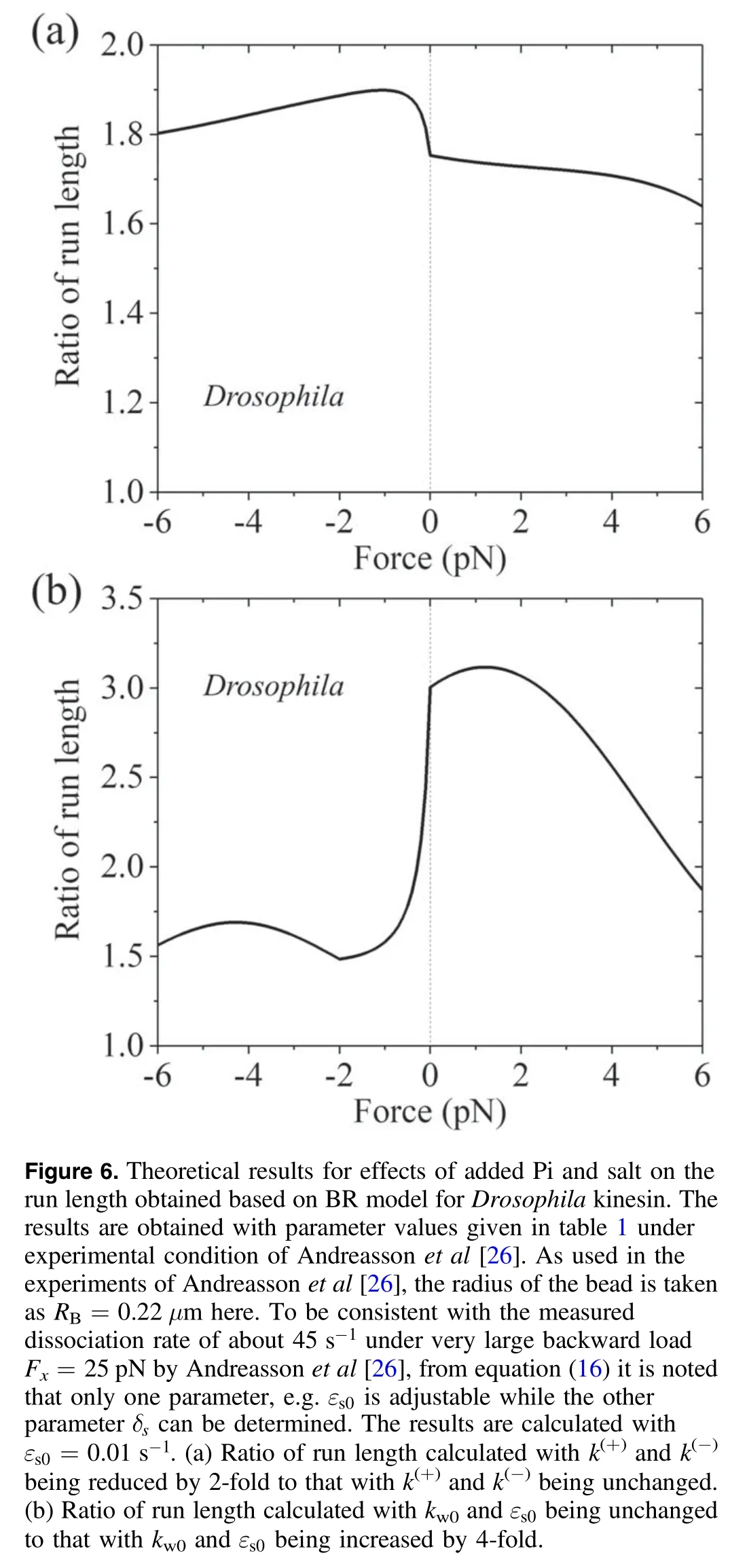
It is mentioned that in the BR model in any MT-binding state (e.g.the weak MT-binding state with affinity Ew1,the weak MT-binding state with affinity Ew2,or the strong MTbinding state) kinesin shows slip bonding to MT,with the dissociation rate increasing exponentially with the increase in the magnitude of the load,consistent with Kramers theory.During the processive motion,however,the occurrence rate of the weak MT-binding state with affinity Ew1depends on the loading direction,resulting in the dramatic asymmetry of the dissociation rate and thus the dramatic asymmetry of the run length with respect to the loading direction.The occurrence rate of the weak MT-binding state with affinity Ew2,the dissociation rate in the weak MT-binding state with affinity Ew2and the dissociation rate in the strong MT-binding state depend on the magnitude of the backward load,resulting in the slip-catch bond behavior for the dissociation rate under the backward load.
4.Differences between two models
It is evident that the BR model is very different from the NLdocking model.The main differences between the two models are summarized as follows.
4.1.PS versus BR mechanism
In the NL-docking model,the NL docking plays a pivotal role in the forward stepping of the kinesin motor.The forward stepping of the kinesin is driven mainly by the NL docking.In more details,the forward stepping of the rear ADP-head to the front position is driven by the NL docking of the front head upon ATP binding.As a consequence,kinesin stepping is mainly via the PS mechanism.
In the BR model,upon Pi release the forward movement of the ADP-head from the rear binding site on MT to INT position is driven mainly by the thermal noise.The NLs of finite length between the two heads inhibit the rear ADP-head from diffusing backward to the minus-end binding site next to the rear binding site from which the ADP-head has just detached.Thus,the rear binding site (with the small affinity Ew1to the ADP-head) acts as the ‘reflecting’ boundary and the INT position(with the high affinity to the ADP-head)acts as the ‘absorbing’ boundary for the diffusing ADP-head.After the weakening of the affinity between the two heads the forward movement of the detached ADP-head from the INT position to the front binding site on MT is also driven mainly by the thermal noise,with the NL docking and large conformational change of the MT-bound head providing small energy barriers to prevent the tethered ADP-head from diffusing backward and re-binding to the rear site.As a consequence,kinesin stepping is mainly via the BR mechanism(as implied in the name of this model),with one mechanical step involves two BR processes.The first process is rectified by the effects of the small affinity Ew1and the finite NL length,and the second process is rectified by the effects of the weak affinity between the two heads and the large conformational change and NL docking of the MT-bound head.
In a word,in the NL-docking model the NL docking plays a critical role in the forward stepping of the kinesin motor,while in the PR model the NL docking plays only an assisting role.
4.2.Passive versus active role of MT in motor motility
In the NL-docking model,except for stimulating ADP release,MT acts as a passive track.Thus,MT plays mainly a passive role in the motor motility on MT.In other words,only the motor plays the active role in the relative motion between the motor and MT.
In the BR model,besides stimulating ADP release by MT,the conformational changes of the local MT-tubulin induced by the strong interaction with head inφ,ATP or ADP.Pi state are critical in the rectified BR motion of ADPhead from the rear site on MT to INT position.Thus,MT plays a critically active role in the motor motility.In other words,both the motor and MT play the active roles in the relative motion between them.
4.3.Tight versus non-tight chemomechanical coupling
In the NL-docking model,kinesin behaves tight chemomechnical coupling under any load smaller than the stall force.Namely,the chemomechanical coupling efficiency is kept equal to one under any load smaller than the stall force.
In the BR model,kinesin behaves non-tight chemomechnical coupling under the large backward load although behaves tight or nearly tight chemomechnical coupling under no,forward or small backward load.Namely,the chemomechanical coupling efficiency depends on the external load.
4.4.Force-dependent versus force-independent ATPase rate
In the NL-docking model,since the chemomechanical coupling efficiency is independent of the load,in order to explain the load dependence of velocity it is assumed that the ATPase rate depends on the load.In other words,the decrease of the velocity under the backward load arises mainly from the decrease of the ATPase rate.
In the BR model,it is proposed that the rate of ATP hydrolysis and Pi release(the rate-limiting step of the ATPase activity) is independent of the load,consistent with the available experimental evidence [56].The decrease of the velocity under the backward load arises from the decrease of the chemomechanical coupling efficiency.
5.Concluding remarks
As mentioned in section entitled‘NL-Docking Model’,based on the NL-docking model the following issues are difficult to explain.(i) PAKRP2 dimer,with NL in each head having 32 residues,can also step processively on MT in the hand-overhand manner,also with each forward step of size d = 8.2 nm by hydrolyzing one ATP molecule under no load.(ii) Some kinesin-5 motors can move processively in the minus-end direction,which is opposite to that of NL docking under nearphysiological salt conditions [50].(iii) The NL-docking energy of kinesin-1 is smaller than 10% of the energy required to power a forward step under a load of (6-8)pN.(iv)By completely nullifying the NL docking the kinesin can still move processively towards the MT plus end with a large velocity close to the WT case under a small load.(v) The postulation of the inhibition of ADP release from the rear head to maintain the coordination between the two heads and that of the permission of ADP release from the rear head to explain the ATP-dependent backward stepping are contradictory.(vi) To theoretically reproduce the experimentally measured load-velocity curve,the ATPase rate is required to change greatly with the change of the load on the stalk [3],which is inconsistent with the experimental evidence that changing the strain on the NL has nearly no effect on the ATPase rate of the motor[56].(vii)The theoretical results for ATPase rates of the truncated kinesin monomer and native dimer [3] are inconsistent with the experimental data that the rate of ATP hydrolysis and Pi release of the truncated monomer is nearly equal to that of the dimer [30,57,58].(viii) Under a medium backward load on the stalk (e.g.3 pN or 4 pN),the theoretical results give an evidently two-exponential distribution of dwell times for the forward steps [3],which is contrary to the single-molecule data showing that the dwell-time distribution has a single-exponential form[21,23].(ix) While for the case of load on the stalk the load dependence of ATPase rate can be explained by the loaddependent effect of NL on its head [59],for the case of load on one head via an external linker it is puzzling how the load affects more sensitively the ATPase rate [60].(x) While the experimental data showing that the presence of added salt reduced greatly the run length under a 4 pN backward load[61] can be explained easily,it is very puzzling that the presence of added salt had a small effect on the run length under a 4 pN forward load [61].
By contrast,based on the BR model,the above puzzling issues can be explained well and readily [3,35-38,68,81].Moreover,diverse available experimental data on the dynamics of different families of N-terminal kinesin motors such as kinesin-1,kinesin-2,kinesin-3,kinesin-5 and orphan kinesin PAKRP2 can be explained quantitatively and consistently [35-38,70-73,76,81].All these support the BR model.In addition,it is interestingly noted with the similar model for dimeric myosin-V molecular motor,diverse available experimental data about dependences of velocity,run length,etc,upon load and ATP concentration and in particular the puzzling catch-bond characteristic for dissociation rate of myosin-V can also be reproduced very well [82,83].To further verify the BR model,it is required in future to test the prediction that under a large backward load multiple ATP molecules are consumed per mechanical step (figure 4).For example,using single-molecule optical tweezers complemented with using a fluorescent ATP analogue (deacaminoATP),the processive stepping and nucleotide binding/dissociation under load can be measured simultaneously,similar to that used by Sakamoto et al [84] to study the chemomechanical coupling of dimeric myosin-V motor.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No.11775301).
Appendix.Correlations among the large conformational change of the head in ATP or ADP.Pistate,weakening its affinity with the detached ADPhead and its NL docking in BR model
When the head is inφstate its NBP is in the open form.ATP binds firstly to the open NBP and then NBP can close,which is associated with the large conformational change of the kinesin head [63].Evidently,ATP has a high rate to dissociate from the open NBP,while has a small (nearly zero)rate to dissociate from the closed NBP.For the front head,with the NL in the backward and horizontal direction(parallel to the MT filament),due to the NL interference NBP closing and the large conformational change cannot occur.For the rear head,with the NL in the forward direction,the NL does not interfere with NBP closing and the large conformational change.For the MT-bound head in INT state,even under the backward load used in optical trapping experiments with micrometer-sized beads the NL of backward direction forms an angle more than 45°with the horizontal direction[85],and thus the NL still does not interfere with NBP closing and the large conformational change.As showed elsewhere[37,38,76],with the above proposal of NL-directiondependent NBP closing and on the basis of the BR model reviewed here the available single molecule experimental data on dependences of velocity,stepping ratio,dwell time,etc,upon the load and ATP concentration can be reproduced well.
The large conformational change of the kinesin head induces the rotation ofα6 helix(to which the NL strandβ9 is connected) relative toα4 helix (which is bound fixedly to MT) [64].Then,the NL docking can occur by forming a cover-neck bundle between the NL strandβ9 and motor domain strandβ0 [24,43].The conformational change of the MT-bound head also induces the large reduction of its binding energy with the detached ADP-head,which is consistent with the atomistic MD simulations [40].Thus,both the large reduction of the binding energy of the MT-bound head to the detached ADP-head and the NL docking can occur almost simultaneously,with the rate determined by the conformational change of the MT-bound head.
 Communications in Theoretical Physics2021年5期
Communications in Theoretical Physics2021年5期
- Communications in Theoretical Physics的其它文章
- A simplified Parisi ansatz
- New holographic Weyl superconductors in Lifshitz gravity
- Electron acoustic solitary waves in unmagnetized nonthermal plasmas
- Vector kink-dark complex solitons in a threecomponent Bose-Einstein condensate
- Ab initio study of the effects of helium on the mechanical properties of different erbium hydrides
- A pedagogical review on solvable irrelevant deformations of 2D quantum field theory
