A simplified Parisi ansatz
Simone Franchini
Sapienza Università di Roma,1 Piazza Aldo Moro,00185 Roma,Italy
Abstract Based on simple combinatorial arguments,we formulate a generalized cavity method where the Random Overlap Structure (ROSt) probability space of Aizenmann,Sims and Starr is obtained in a constructive way,and we use it to give a simplified derivation of the Parisi formula for the free energy of the Sherrington-Kirkpatrick model.
Keywords: Sherrington-Kirkpatrick model,cavity methods,Parisi formula
1.Introduction
Some decades ago a very sophisticated mean-field (MF)theory was developed by Parisi to compute the thermodynamic properties of the Sherrington-Kirkpatrick (SK)model in the low-temperature phase [1-6].In his theory,that is obtained within the larger framework of the replica theory[2,5],Parisi introduced many important concepts that are now standards in the field,like the overlap distribution as an order parameter and the nontrivial hypothesis that the scalar products between independent replicas of the system (overlaps) concentrate on a numeric support that is ultrametrically organized [2,3,5,7-13].
After many years Guerra [3] and Talagrand [4] showed that this remarkable MF theory indeed provides the correct expression for the free energy of the SK model,while Panchenko proved that the SK Gibbs measure can be perturbed into a special cascade of point processes (Ruelle cascade[9,10]) that gives the same free energy and indeed satisfies the ultrametricity assumption [10,13].These mathematical milestones and many other theoretical and numerical tests(see [6] and references) contributed to form the idea that,at least for MF models,this ansatz provides the correct physical properties.
Following simple combinatorial arguments we show that the same results of the replica symmetry breaking (RSB)theory can be obtained in a constructive way without relying on the replica trick,or averaging on the disorder.After presenting a general analysis of the SK Hamiltonian,we will show that the usual assumptions associated with L levels of RSB(see[2,8-10,14])are consistent with a hierarchical MF theory in which the states ensemble is charted according to a sigma algebra generated by a partition of the vertex set.The method provides a constructive derivation of the Random Overlap Structure (ROSt) probability space introduced in [8]by Aizenmann,Sims and Starr.We further tested this by computing the corresponding incremental pressure that one obtains from the cavity method [2,8,9],and it indeed provides the correct Parisi functional.
We start by introducing the basic notation.Let us consider a spin system of N spins; we indicate the spin sites by the vertex setV= {1 ,2,… ,N},marked by the label i.A unique spin variableσithat can be plus or minus is associated with each vertex.Formallyσi∈Ω,hereafter we assume Ω = {+ ,-},although our argument holds for any size of ∣Ω ∣(for this paper a modulus∣·∣applied to a discrete set returns its cardinality,for example∣V∣=N).We collect the spins into the vector
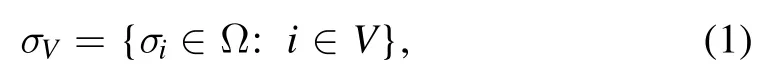
that is supported by the N-spin vector space ΩV,and we call these vectors magnetization states.Notice that we implicitly established an arbitrary reference frame on V by labeling the spins.
Let J be some matrix of entriesJij=O(1).Even if the arguments we are going to present are not limited to this case,in the following we also assume that the Jijentries are random and normally distributed.Then,the Sk model without an external field is described by the Hamiltonian
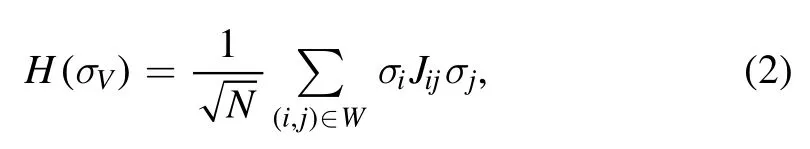
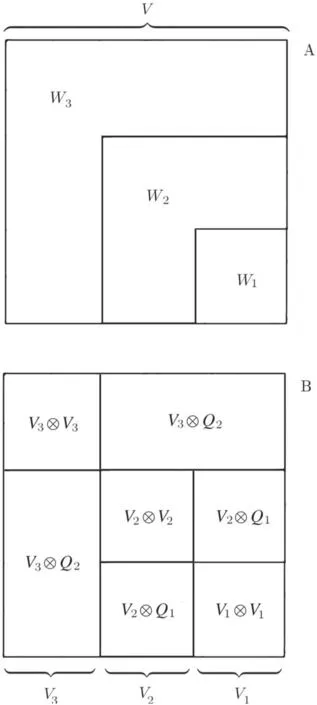
Figure 1.Figure A shows the partition of V ⊗V following that of V for L = 3.The edges set is split into subsets Wℓ containing all the edges with both ends in Qℓ minus those with both ends inQℓ -1.The bottom figure (B)is intended to explain the structure of Wℓ in terms of layers of spins: Vℓ ⊗Vℓ contain the edges between the spins of Vℓ,while Vℓ ⊗ Qℓ -1 and Qℓ - 1 ⊗Vℓcontain the edges that make the interface between the layer Vℓ and the rest of the system.
whereW=V⊗Vis the edges set accounting for the possible spin-spin interactions andis a normalization that in MF models can be∣V ∣- dependent.In the SK model the interactions are normally distributed and we have to take a normalization that is the square root of the number of spins∣V ∣ =N,but the same analysis can be repeated for any coupling matrix and its relative normalization.As usual,we can define the partition function
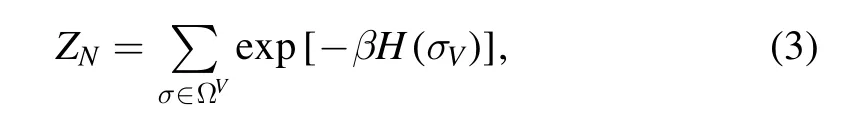
and the associated Gibbs measure

The free energy density is written in terms of the pressure
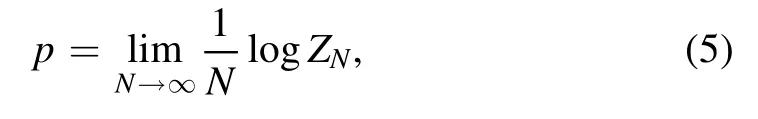
and the free energy per spin is given by
A variational formula for the pressure of the SK model has been found by Parisi [1].Following this,and after[2,8-10]it has been proven that the average pressure per spin can be computed from the relation
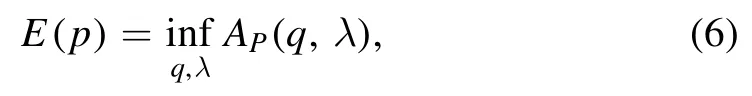
whereAP(q ,λ) is the Parisi functional of the (asymmetric)SK model,as defined in equation (3); hereafter,for the noise average we use the special notationE(·).
The minimizer is taken over two non-decreasing sequences q = {q0,q1,… ,qL} andλ = {λ0,λ1,… ,λL} such that q0=λ0=0and qL=λL=1.The Parisi functional is defined as follows
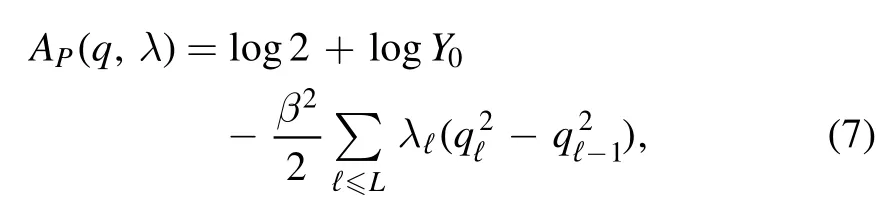
where to obtain Y0we apply the recursive formulato the initial condition
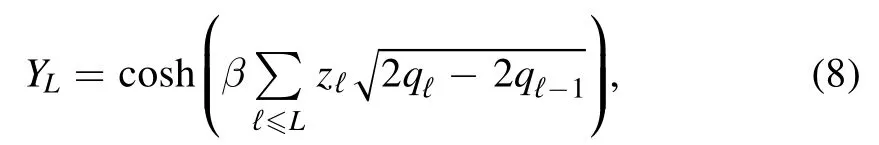
with zℓi.i.d.normally distributed andEℓ(·) the normal average that acts on zℓ.Notice that we are using a definition where the temperature is rescaled by a factorwith respect to the usual Parisi functional.This is because the Hamiltonian H (σV)does not represent the original SK model,where in the coupling matrix the contribution between spins placed on the vertex pair (i ,j) is counted only once,but the so-called asymmetric version that has independent energy contributions from both (i ,j) and the commuted pair (j ,i).The functional for the original SK model is recovered by substituting β with β.
2.Martingale representation
Let us partition the vertex set V into a number L of subsets Vℓ,with ℓ from 1 to L.Notice that by introducing the partition Vℓwe are implicitly defining the invertible map that establishes which vertex i is placed in which subset Vℓ,but,as we shall see,the relevant information is in the sizes∣Vℓ∣ =Nℓand we do not need to describe the map in detail.The partition of V induces a partition of the state
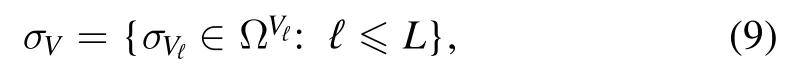
and its support.We call the sub-vectorsσVℓthe local magnetization states of σVwith respect to Vℓ,formally
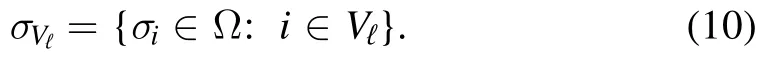
From the above definitions we can construct the sequence of vertex sets Qℓthat is obtained by joining the Vℓsets in sequence,according to the label ℓ


composed by the first ℓ sub-statesσVℓ.Also,in this case,hold the relations=σVℓandσQL=σV.Notice that the sets Vℓare given the differences between consecutive Qℓsets,then
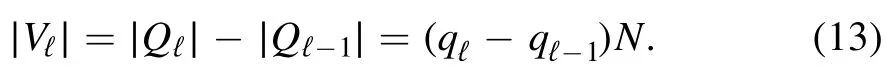
In this section we will show a martingale representation for the Gibbs measureμ(σV),where we interpret the full system as the terminal point of a sequence of subsystems of increasing size.Formally,we show that one can splitHσ(V)into a sum of ‘layer Hamiltonians’
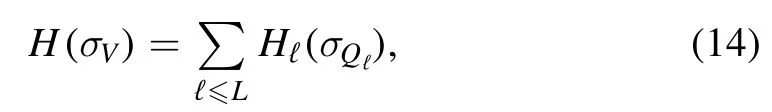
with each Hℓdescribing the layer of spins Vℓplus an external field that accounts for the interface interaction with the previous layer.
To prove this we first notice that the partition of the edges set W induced by that of V is into subsets Wℓthat contains the edges with both ends in Qℓminus those with both ends inQℓ-1; this is also shown in figure 1A,where the edges(i,j)are represented as points on the squareV⊗V.The HamiltonianHσ(V) can be written as a sum of layer Hamiltonians defined as follows

and each contains the energy contributions fromThe total number of energy contributionsσi Jij σjgiven by Wℓis
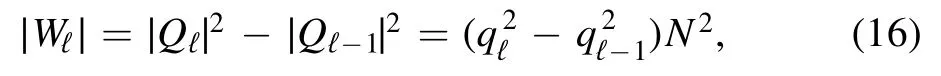
that already unveils a familiar coefficient of the Parisi formula.We can further rearrange the components of the layer contributions by noticing that
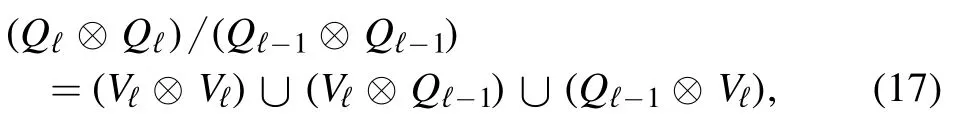
where the right side of the equation is also shown in figure 1B.Then,the energy contributions coming from Wℓcan be rewritten as follows
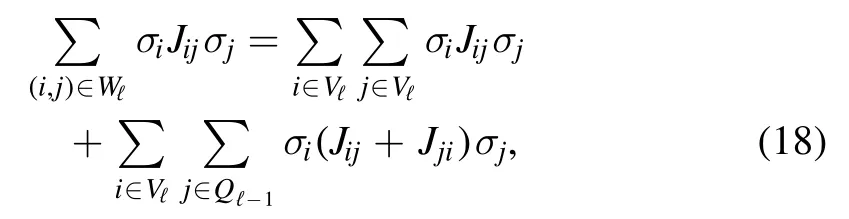
and we can identify two components; one is the layer selfinteraction that depends only on the spinsσVℓ
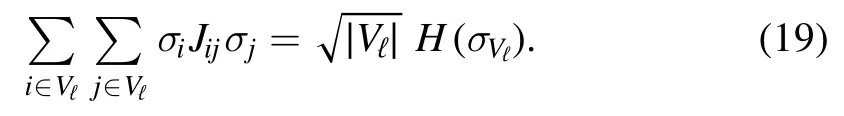
The second contribution can be interpreted as the interface interaction between the layers.Let us define the interface fields
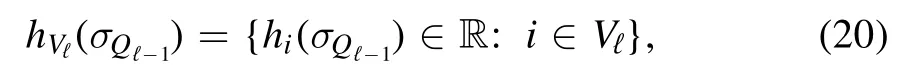
where the individual components are defined as follows

then the interface contributions can be written in terms of a perturbation depending on the preceding layers.Putting these definitions into the previous equation we find that the SK Hamiltonian can be written as a sum of the layer energy contributions

Notice that the contributions of theℓ- th level only depend on the spins of Vℓand the previous Vtfort<ℓ,but not on those for t > ℓ; this is expression of the fact that the original system is reconstructed through an adapted process,in which we start from the unperturbed seedHσ(V1) of N1spins and then add layers of Nℓspins until we reach the size N.Also,notice the coefficientin front ofH(σVℓ)that is due to the N-dependent normalization of the SK Hamiltonian.This coefficient is special for fully connected random models;for a fully connected static model,like the Curie-Weiss,it would have been of the orderqℓ-qℓ-1,while for models with finite connectivity the coefficient isO(1),as we shall shortly see.
From the last equations we find the corresponding partition of the Gibbs measure.The partition function is obtained from the formula
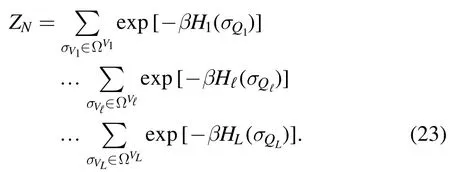
Let us introduce the ‘layer distributions’

with the layer partition functions given by

It is easy to verify that their products give back the original Gibbs measure

but notice that the relative weightsξ ℓ(σQℓ) are measures themselves and sum to one inσVℓ
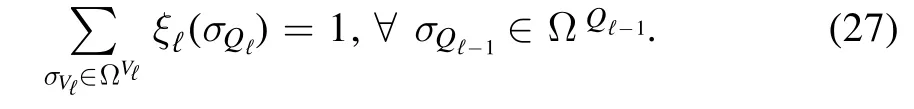
We can finally write the martingale representation we were searching for.Consider the test functionf: ΩV→ℝ;then,applying the previous definitions the average〈f(σV)〉μwith respect to μ is obtained through the following backward recursion.The initial condition isfL(σQL) =f(σQL),whereQL=V,then we iterate the formula

backward until the first stepℓ= 0 that gives the average of f with respect to the Gibbs measure μ.This result is an expression of the Bayes rule and can be easily derived starting from the identity
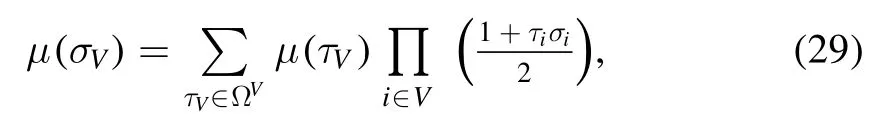
and substituting the definitions given before in that of〈f(σV)〉μbrings us to the desired result.Notice that up to now our manipulations are based on general principles and do not require any special assumption concerning the Hamiltonian.
Before going further we remark that these arguments are not limited to MF models.For example,we can easily extend this description to the Ising spin glass in finite dimensions.
Let Λ be the adjacency matrix of the hyper-cubic latticeℤdand substitute the Hadamard product Λ◦Jon behalf ofJandon behalf ofwhere the normg(Λ) is the average number of nearest neighbors of a vertex according to Λ,
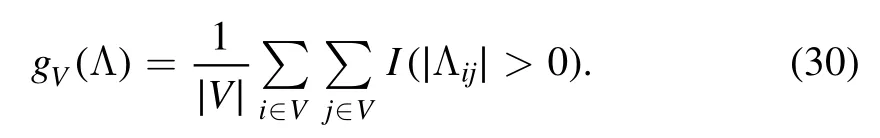
If the adjacency matrix Λ is that of a fully connected graph we takeg(Λ) =∣V∣and recover the SK model,otherwise forℤdisg(Λ) =2d.The result is the following generalized Hamiltonian
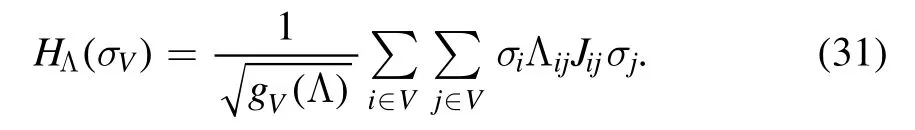
If the adjacency matrix is fully connected,which is the case for the SK and other MF models,there is no underlying geometry associated with V and we can grow the system to the size we want.In finite dimensional models,however,we may have additional constraints.In the finite dimensional case,to grow an Ising spin glass onℤdwe should consider a cube that is enclosed in a larger cube and so on.To enclose a hyper-cubic region ofℤdof side length r and volume rdinto a larger region of side r + k we need at least (r+k)d-rdnew sites to add,so the sizes of the V partition should satisfy the relationor equivalentlyfor some integer sequence rℓ.
Due to the presence of gV(Λ)nearest neighbors to each site,each layer contributes to the total energy with∣Wℓ∣ =gV(Λ)∣Vℓ∣edges,each multiplied by its coupling Jij.Apart from this,the partition works in the same way
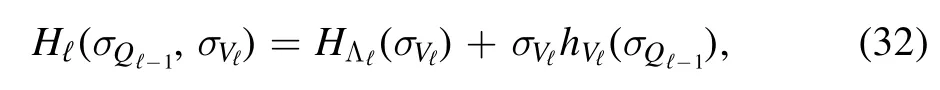
where the local contributions are defined as follows
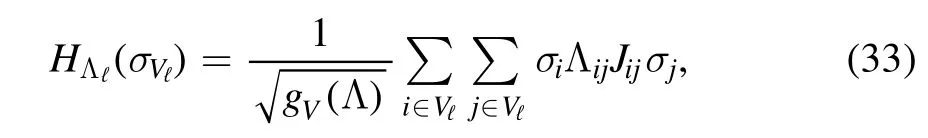
and the cavity fields again incorporate the interface interaction between the layers
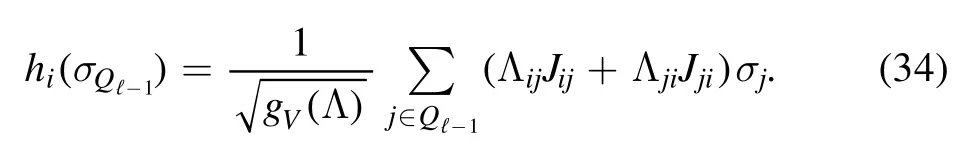
For this paper we concentrate on the MF description.
3.Incremental pressure
To make the previous formulas effective we need a way to express the pressure in terms of the Gibbs measure.This can be done by the cavity method [2,8,14],i.e.by relating the partition function of an N-spin system to that of a larger(N+ 1)- system and then computing the difference between the logarithms of the partition functions.
In this paper we follow a derivation in [7]originally due to Aizenmann et al [8],see also [9,10].Define the cavity variables,i.e.the cavity field
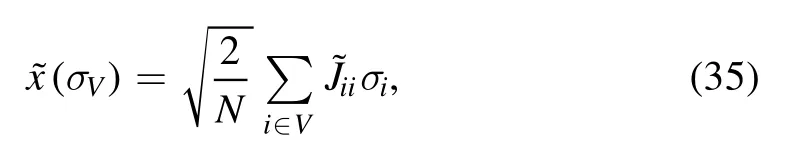
and the so-called ‘fugacity term’ (see[8])
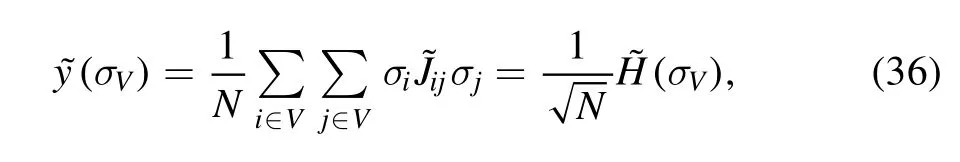
that is proportional to the Hamiltonian in distribution,with a different noise matrix.First,we apply the Gaussian summation rule
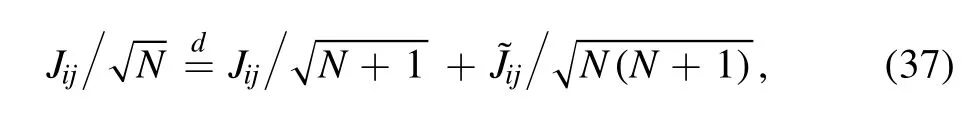
to the Hamiltonian of the N-system to isolate the fugacity term.The matrixJ~is a new noise independent from the J.The following relation holds in distribution
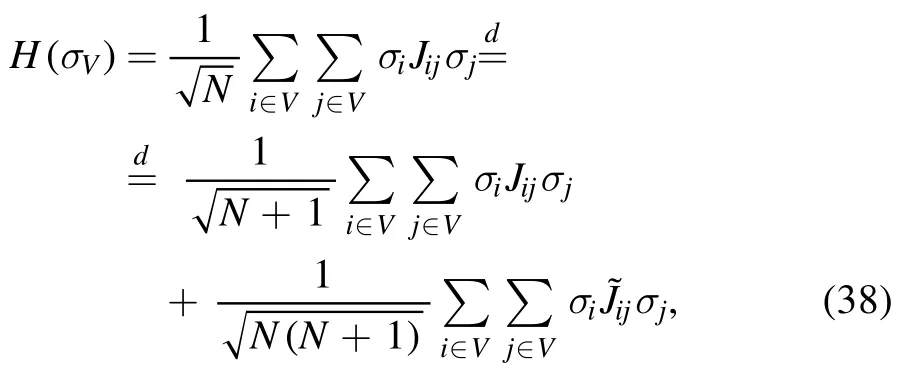
using the definition ofthe partition function is written as

and notice that the average is with respect to an N-system at slightly shifted temperature.Now,considering the system ofN+1 spins,we separate the last spin to find
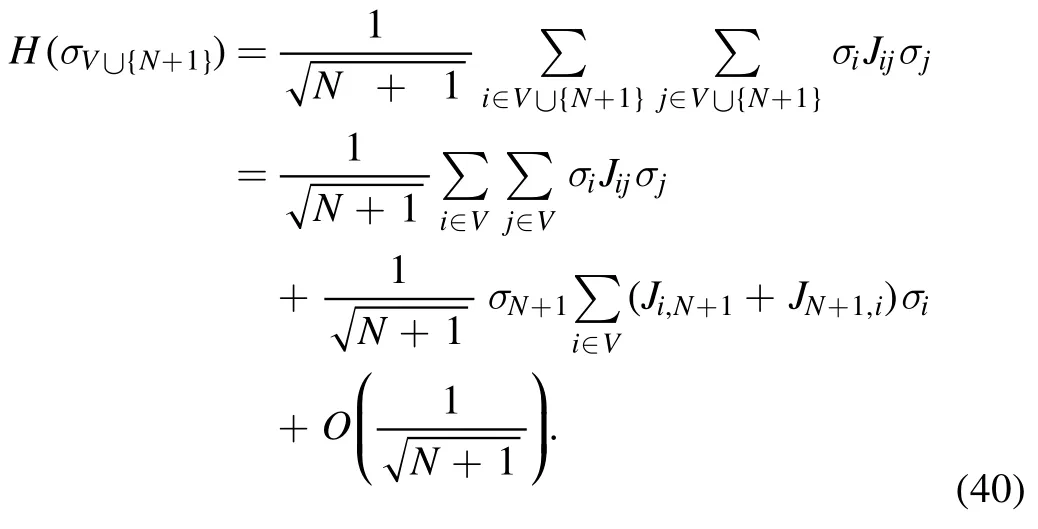
Since the sequenceJi,N+1and its transpositions are independent from the other J entries and also between themselves,we can write a more pleasant formula by using the diagonal terms ofon its behalf,i.e.we again use the Gaussian summation rule
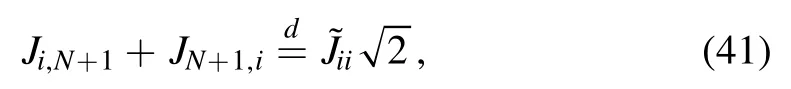
where the superscript d specifies that the equality holds in distribution.The noise relative to the vertexN+ 1 is written entirely in terms of thematrix.The associated partition function is computed by integrating the spinσN+1,and one obtains
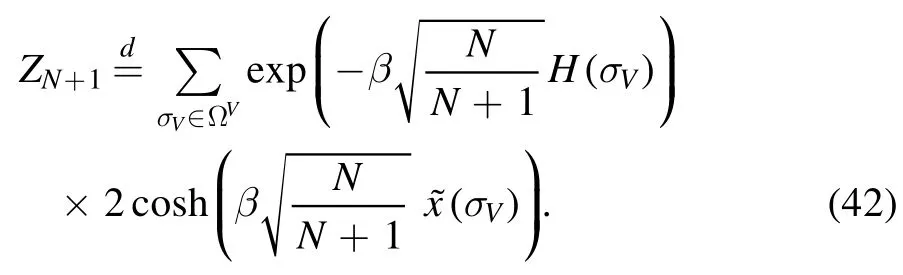
Now,both partition functions are rewritten in terms of the N-system at a rescaled temperature
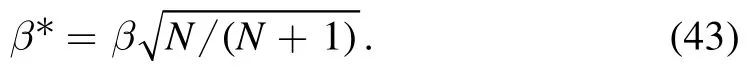
We distinguish the rescaled partition function from ZNwith a star in superscript
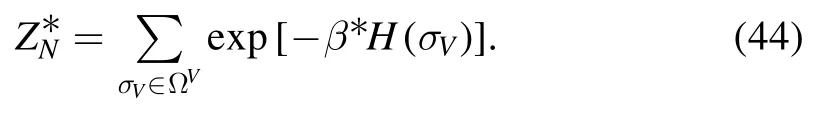
Dividing bothZN+1and ZNbywe can eventually write the incremental pressure in terms of the measure
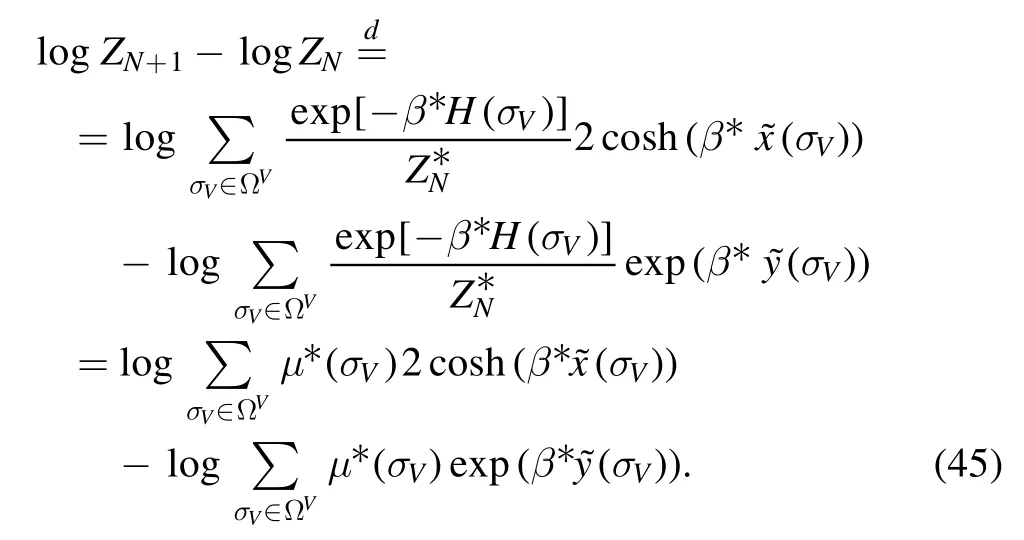
Then,apart from a rescalingβ*→βand other terms that are negligible in the thermodynamic limit the pressure can be bounded from below by the incremental pressure functional,
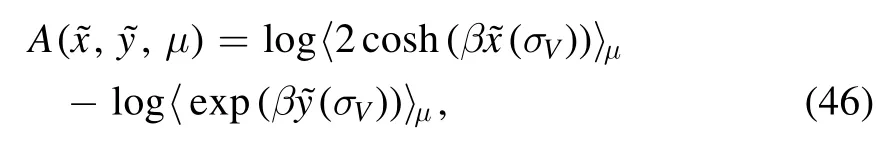
because the pressure is always bounded from below by the limit inferior of the incremental pressure
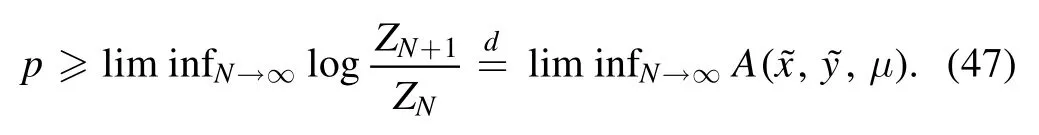
Until this point the analysis is well known.Let us now apply some considerations from the previous section to the cavity variables.The cavity field is easy,as it is natural to split
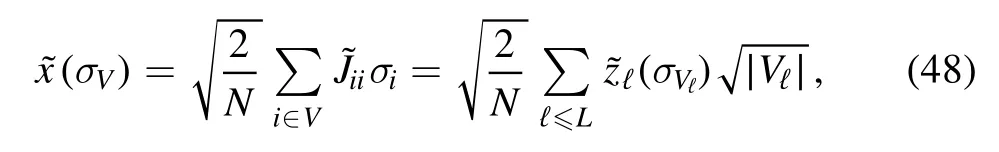
into independent variables that are functions of the Vℓspins only

The fugacity term is distributed like the Hamiltonian,and then we can use the same arguments as before and write the decomposition

where we introduced the new variable
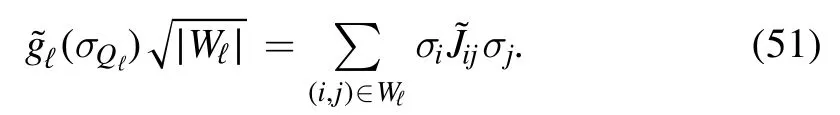
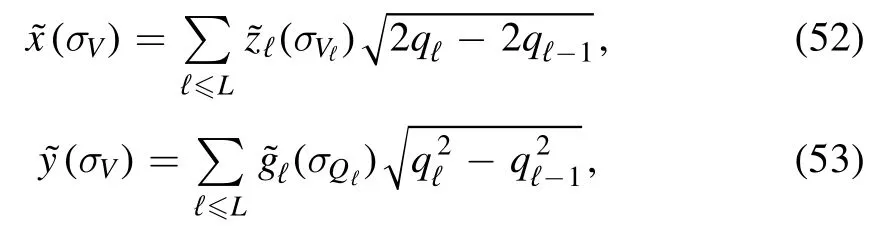
and match that of the ROSt probability space first introduced in[8].Indeed,this is precisely the point where the martingale representation before plays its role,as it allows us to bridge between the pure state distributions described in [2],that we can identify with the following products of layer distributions
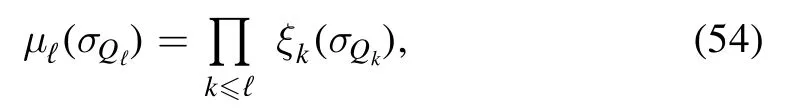
and the ROSt probability space given in [8],with all its remarkable mathematical features.
Put together the functional becomes
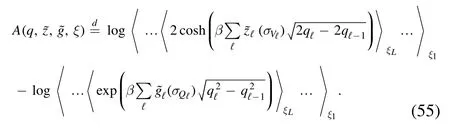
In computing the previous formula we made the natural assumption that the partition used to split the HamiltonianH(σV) should be the same as that used to split the terms that appear in the cavity formula,then the dependence of A on q is both explicit and through the distributions ξℓ.It only remains to discuss the averaging properties of the layer distributions.
4.Simplified ansatz
We start by noticing that due to the vanishing coefficientin front ofH(σVℓ) this contribution in equation(22)can actually be neglected in theL→∞limit.If we introduce the rescaled temperature parameter
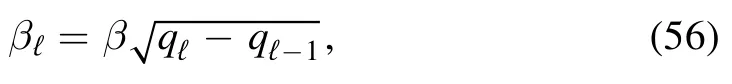
that can be made arbitrarily small in theL→∞limit,then we can rewrite each layer in terms of an SK model of size Nℓat temperature βℓ

subject to the (strong) external field

whose magnitude diverges in theL→∞limit due to thenormalization.Then,for any finite temperature β we can make N and L large enough to have a qℓsequence for whichβℓ<βcat any ℓ,and it has been established since[11]and [12] that in the high-temperature regime the annealed averages needed to compute equation (55) match the quenched ones (the layers are replica symmetric).
To make this argument more precise let us consider the Hamiltonian

in the thermodynamic limit,and forL→∞one can compute the averages in equation (28) according to the Hamiltonianinstead ofHℓ(σQℓ); this will be shown at the end of this section.The partition function of themodel can be computed exactly and one finds
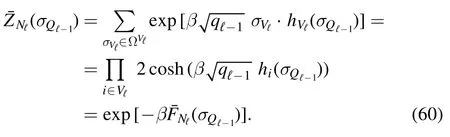
Moreover,following[2],from the Boltzmann theory one can show that at equilibrium the logarithm of the associated Gibbs distribution is proportional to the fluctuations around the average internal energy
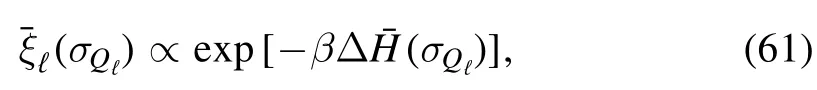
where the fluctuations are defined as follows
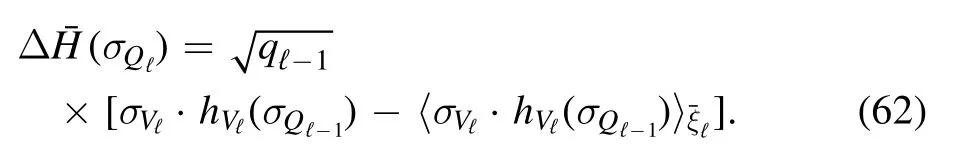
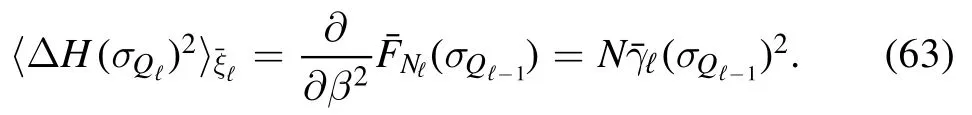
Then,under the Gibbs measurethe energy fluctuations can be approximated in distribution by a Derrida’s random energy model (REM,see [7,10])

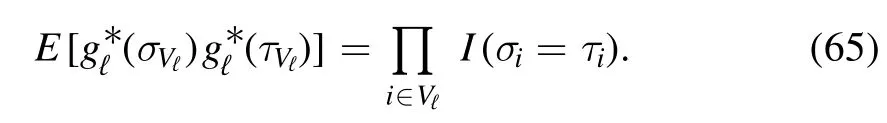
Since the SK measure is weakly exchangeable,althoughmay depend on the spins ofσQℓ-1through the cavity fieldshVℓ(σQℓ-1),the only way to enforce this invariance is to admit that eventually

under ξℓaverage for some positive numberNotice thatindependent ofσQℓ-1does not mean that the sign ofis fixed,and under the full measureone may have different correlations between the full statesσQℓdue to the averaging effect ofon the interface fields.The term∈ ℓ(N) in equation (64) is a constant that does not depend on the spins and we can interpret it as the deterministic component ofHℓ(σQℓ) under Gibbs measure; for the SK model we expect∈ ℓ(N) =0for all ℓ,but its exact value is not important in computing the Parisi functional because in the end it will wash out due to the difference between the logarithms.
Before discussing the physical features let us verify that the simplified ansatz provides the correct Parisi functional.As shown in[9],the thermodynamic limit of a Gaussian REM of amplitudeis proportional in distribution to a Poisson point process (PPP) of rate
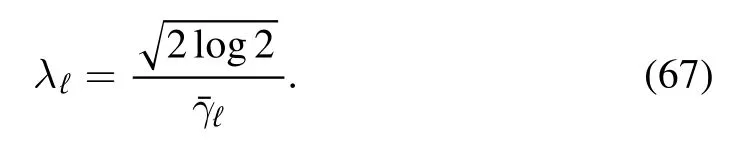
The system at equilibrium is then decomposed into a large (eventually infinite) number L of subsystems,one for each vertex set Vℓ,whose Gibbs measures are proportional in distribution to a sequence of Poisson-Dirichlet (PD) point processes,i.e.the Gibbs measures that describe the layers are proportional in distribution to PPPs[9,10]of rate λℓ,that is a function of q but independent from the spinsσQℓ-1.
By the special average property of the PPP [9,10] (see also the Little theorem of [14]) for any positive test functionf: ΩN→ ℝ+we have
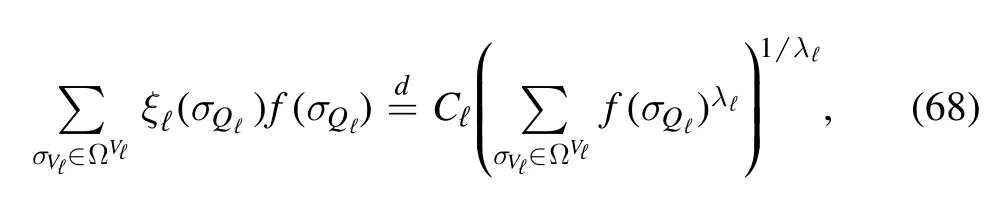
for some constant Cℓthat may depend on β but not on the spins.Then,the random average〈f(σV)〉μis obtained through the following recursion
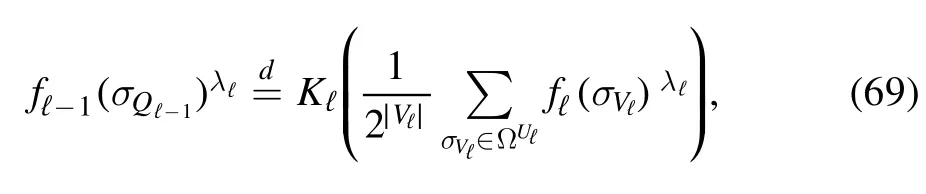
that holds in distribution,withThis allows us to compute the main contribution
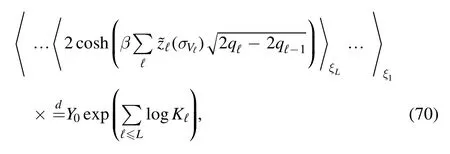
by applying the recursive relation
to the initial condition
down to the lastℓ= 0.Notice that in the recursion the average overσVℓis uniform; under uniform distribution bothandare normally distributed and independent from the previous spin layersσQℓ-1,then we can take
with zℓand gℓi.i.d.normally distributed,and change the uniform average overσVℓinto a Gaussian average Eℓacting on these new variables.We compute the fugacity term in the same way,

Put together the contributions depending on Kℓcancel out and one finds
that is exactly the Parisi functional as is defined in the introduction.Notice that in this equation and in the previous we implicitly assumed that the sequences q and λ are exactly those that approximate the SK model.The lower bound in the variational formula can be easily obtained from the knowledge of the Parisi functional by minimizing on the possible sequences q and λ
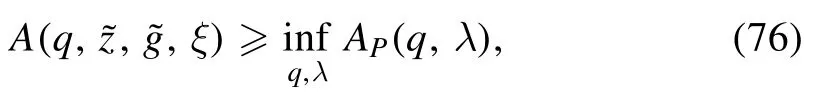
while the upper bound can be checked,at least for the SK model,by Guerra-Toninelli interpolation [3].
It remains to be proved that one can compute the averages in equation (28) according to the Hamiltonianinstead ofHℓ(σQℓ),consider the full layer distribution

define its version without an external field
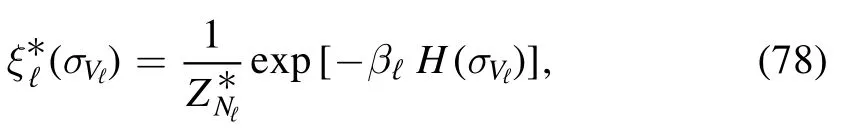
that is simply an SK model at (eventually high) temperatureNow,if we assume the thermodynamic limit exists we can use the Boltzmann theory and express the thermodynamic fluctuations as though they were a Gaussian set.Start from the general average formula
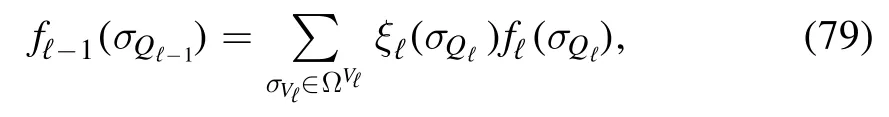
using the REM-PPP relation onHσ(Vℓ) and the PPP average properties one finds that the formula for the partition function is
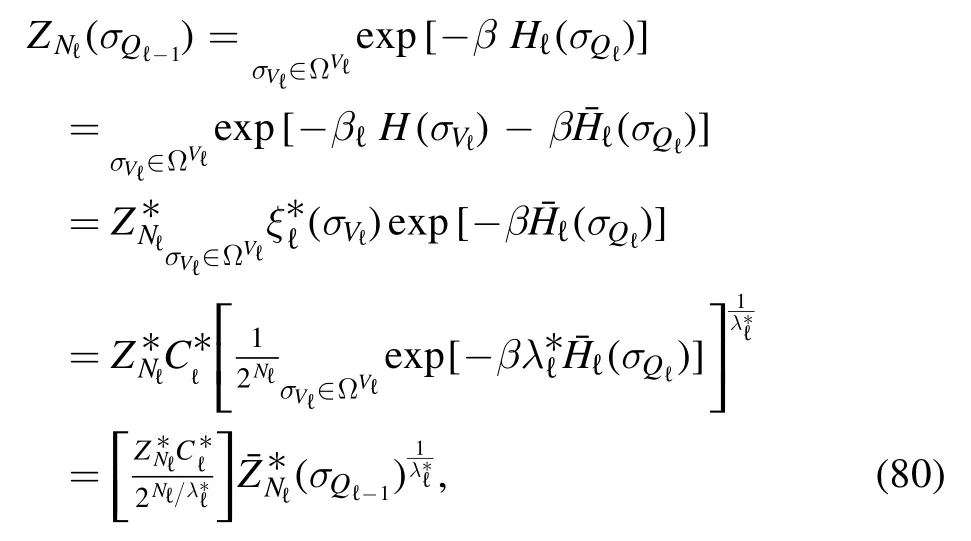
wheres the rate of the associated PPP.In the last two steps we introduced the partition functionassociated with themodel at slightly rescaled temperatureLetbe the Gibbs measure associated with themodel at the rescaled temperaturethen the formula for the average becomes

and putting everything together simplifies to
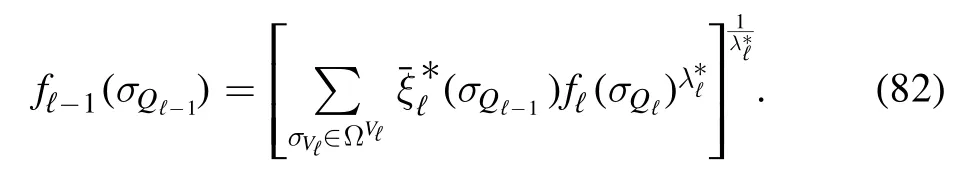
This formula does not depend on N and then also holds in the thermodynamic limitN→∞,where we can actually take βℓto zero,and applying to the recursion one would find
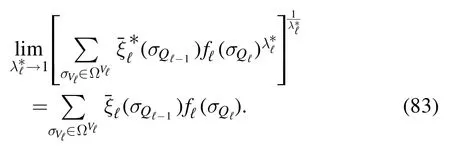
The idea is that for positive fℓand in the limitqℓ-qℓ-1→0 one would find that the SK average is taken at infinite temperature,then equivalent to a PPP of rate→1.
5.Conclusive remarks
Even if we easily obtained the functional,from the physical point of view this short analysis still did not clarify what is the proper approximation forunder the full measure μ(see figure 2).If one assumes that the same approximation used under ξℓalso holds under μ it would be equivalent to assert that
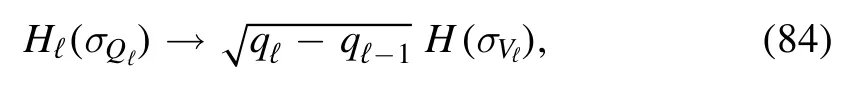
and then the model would simply be a sum of smaller independent systems at higher temperatures.By the way,we remark once again that for large L the coefficientsqℓ-qℓ-1vanish with respect toqℓ-1,and it is unlikely that this ansatz can return stable solutions in any fully connected model.
In fact,this would be a quite orthodox MF ansatz [15],where the external field acting on the layer is irrelevant,although in the SK model the number of pairwise energy contributions from the interfaces is much larger than the energy contributions from the spins in the same layer,as already predicted in [16].We expect that the proper approximation under μ would be the generalized random energy model (GREM) [9,10],where

and λℓis the sequence of free parameters that controls the variance,andgℓ(σQℓ) is a collection of normal random variables of the covariance matrix
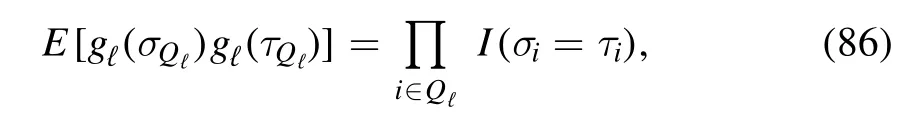
withE(·) representing the normal average that acts on the variablesgℓ(σQℓ).The difference with the orthodox MF ansatz is in that by changingwithgℓ(σQℓ) for any magnetization states σVandτVwithnow one has

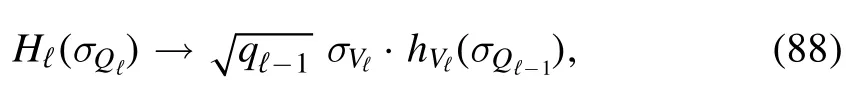

Figure 2.Two extreme pictures for the RSB ansatz for L = 3.The diagram shows the edges that contribute to the energy in the orthodox MF ansatz,top figure A,where the Hamiltonian operator is diagonal under Gibbs measure,and a situation where the interfaces dominate the total energy,lower figure B.We expect the second option to be much more likely for fully connected models,because in such models the interfaces are overwhelmingly large with respect to the contribution from edges between spins of the same layer.
which indeed seems the case for any fully connected MF model,at least.Notice that in the thermodynamic limit the associated Gibbs measure is distributed proportionally to a cascade of PPP,known as the Ruelle cascade[8-10,13],that is known to have an ultrametric overlap support.For the SK model this property was first proven in[13],where it is shown that the Gibbs measure of the SK model can be infinitesimally perturbed into a Ruelle cascade.
In conclusion,it seems not possible to distinguish between the orthodox MF ansatz (the Gibbs measure is a product measure) from the RSB ansatz (the measure is a Ruelle cascade) by only looking at the Parisi formula.Nonetheless,we argue that the orthodox MF theory is unlikely to hold in the SK model,due to expected dominance of the interface contribution.Whether an orthodox MF ansatz is meaningful in some sense for the SK model we still cannot say,although it seems related to the replica trick.Despite this,we think it would naturally apply to many other disordered systems,like random polymers,or any other model with low connectivity between the layers.
Acknowledgments
I wish to thank Amin Coja-Oghlan (Goethe University,Frankfurt) for sharing his views on graph theory and replica symmetry breaking,which deeply influenced this work.I also wish to thank Giorgio Parisi,Pan Liming,Francesco Guerra,Pietro Caputo,Nicola Kistler,Demian Battaglia,Francesco Concetti and Riccardo Balzan for interesting discussions and suggestions.This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme(Grant Agreement No [694925]).
 Communications in Theoretical Physics2021年5期
Communications in Theoretical Physics2021年5期
- Communications in Theoretical Physics的其它文章
- Insight into the chemomechanical coupling mechanism of kinesin molecular motors
- A pedagogical review on solvable irrelevant deformations of 2D quantum field theory
- Ab initio study of the effects of helium on the mechanical properties of different erbium hydrides
- Interface water-induced hydrophobic carbon chain unfolding in water
- Vector kink-dark complex solitons in a threecomponent Bose-Einstein condensate
- Electron acoustic solitary waves in unmagnetized nonthermal plasmas
