A pedagogical review on solvable irrelevant deformations of 2D quantum field theory

Yunfeng Jiang

CERN Theory Department,Geneva,Switzerland

Abstract This is a pedagogical review on deformation of two dimensional quantum field theories.It is based on three lectures which the author gave at ITP-CAS in December 2018.This review consists of four parts.The first part is a general introduction to deformation.Special emphasises are put on the deformed classical Lagrangian and the exact solvability of the spectrum.The second part focuses on the torus partition sum of thedeformed conformal field theories and modular invariance/covariance.In the third part,different perspectives of deformation are presented,including its relation to random geometry,2D topological gravity and holography.We summarize more recent developments until January 2021 in the last part.

Keywords:irrelevant deformation,integrability,conformal field theory,2D gravity,holographic duality

1.Introduction

Quantum field theory(QFT)provides an important theoretical framework for understanding nature.The space of QFTs can be explored with the help of renormalization group (RG).Conformal field theories constitute the fixed points of RG flow.Understanding conformal field theory is an important question and is now under intensive study.

At the same time,it is equally interesting to study the flows away from fixed points.Depending on the operators that trigger the flow,the deformations of QFTs can be divided into three broad classes,namely relevant,marginal and irrelevant.While there have been a lot of works on relevant and marginal deformations of QFT,irrelevant deformations of QFTs are largely unexplored,for good reasons.By standard arguments of renormalization theory,irrelevant deformations of QFTs necessarily Require an infinite number of counter terms when computing physical quantities.Therefore the Lagrangian involves a tower of infinitely many terms and becomes highly ambiguous.However,it was discovered recently that for certain special classes of irrelevant deformations in two dimensional spacetime,this procedure is under much better control and is even solvable [1,2].This is th e so-calleddeformation,which is the main subject of this review.Apart from thedeformation [1,2],more families of solvable deformations of QFTs have been proposed in the past two years.For theories with a conserved holomorphic U(1) current,one can defnie thedeformation[3].For integrable QFTs which have higher conserved charges,one can defnie a whole family of deformations using the conserved currents [1,4,54].

1.1.Solvability of deformation

Thedeformation is triggered by the irrelevant operator= - det(Tμν).Although thedeformation folws towards UV,many physically interesting quantities can be computed exactly and explicitly in terms of the data from the undeformed theory.More precisely,these quantities include the S-matrix,the deformed classical Lagrangian,the finite volume spectrum on an infinite cylinder and the torus partition function.We give a brief discussion on these quantities in what follows.

The S-matrix.The S-matrix is deformed in a simple way underdeformation.The deformed S-matrix is obtained from the undeformed S-matrix by multiplying a phase factor of Castillejo-Dalitz-Dyson type (CDD factor) [6].This deformation of the S-matrix was first conjectured in [7,8] to describe a toy model of quantum gravity.The authors of[7,8]called the multiplication of the CDD factor ‘gravitationl dressing’ because the deformed theory exhibit certain features of gravity.One such feature is non-locality which we will discuss in more detail in this review.Later,the same authors showed that the gravitational dressing of the S-matrix corresponds to thedeformation in the Lagrangian description [9].

Deformed Lagrangian.The definition ofdeformation is given in the Lagrangian description of QFT.We will present this definition in section 2.From the definition,one can derive the deformed classical Lagrangians.It is found that the deformed Lagrangians take very interesting forms[2,10,11].For example,the deformed Lagrangian of a free massless boson takes the form of the Nambu-Goto action in the static gauge.The derivation of this result will be discussed in detail in section 2.More complicated Lagrangians lead to more involved deformed Lagrangians.Due to the complexity of the deformed Lagrangian,it is hard to use them to compute physical quantities at the quantum level.Even so,classical analysis of the deformed Lagrangians give useful hints for some of the features of the deformed quantum theory.

Finite volume spectrum.The surprising feature ofdeformation is that despite the complicated form of the deformed Lagrangian,one can find the finite volume spectrum in a universal way.This is based crucially on Zamolodchikov's factorization formula for the expectation value ofoperator.This interesting formula was first proved by Zamolodchikov in 2004[12].What makes thegreat again after more than a decade is that the authors of [1] and [2] realized that one can perform an irrelevant deformation using this interesting operator.Then the factorization formula results in the solvability of the finite volume spectrum.The deformed spectrum obeys a partial differential equation which is the inviscid Burgers’equation in 1D.This is a well-known equation in fluid dynamics which can be solved explicitly with given initial conditions.We will discuss in detail how to obtain the deformed spectrum in section 3.In integrable QFTs,one can obtain the finite volume spectrum by integrability methods such as thermodynamic Bethe ansatz.The only input for these methods are the factorized S-matrix,which is given by the gravitational dressing as we discussed before.Indeed one finds that the two methods give the same deformed spectrum.

Torus partition function.Given the deformed spectrum in the finite volume,it is natural to study the torus partition function of thedeformed theory.The first interesting result concerning the torus partition function is given by Cardy [13]who derived a diffusion type of differential equation for the partition function.It is proven in [14] that the torus partition function of thedeformed conformal field theory is still modular invariant although the theory is not conformal any more.More interestingly,it is shown in[15]that by requiring modular invariance and that the deformed spectrum depends on the undeformed spectrum in a universal way,one can fix the deformed theory uniquely to be that of thedeformed CFT.A similar analysis can be applied to thedeformed CFT where one replaces modular invariance by modular covariance[16].Section 4 is devoted to a detailed discussion on the torus partition function of theanddeformed CFTs.

1.2.Why is deformation solvable?

As we mentioned above,usually irrelevant deformation is ambiguous,but thedeformation is solvable.A natural question is what is the reason for this solvability? There are different point of views on this.

Integrable deformation.One way to see this is to consider integrable QFT.These theories have infinitely many conserved charges.It is shown that these conserved charges remain conserved along theflow[1].In this sense,it is an integrable deformation.This implies that the deformation preserves an infinite amount of symmetry,which strongly constraints the flow and makes it integrable.

2D topological gravity.Of course,most QFTs are not integrable.However,thedeformation is defined for any QFT.There must be other ways to understand the solvability ofdeformation.One such point of view is provided by Cardy's random geometry picture[13].It is shown that the infniitesimal deformation of the partition function byis equivalent to integrating over the variations of the underlying spacetime geometry.The ‘gravity sector’ which governs the possible variations turns out to be a total derivative.This implies that the‘gravity sector’ related to the infinitesimaldeformation is solvable.Related to this more geometrical picture,it is proposed in[9]that turning ondeformation for a QFT is equivalent to coupling the theory to a specifci 2D topological gravity,which is very similar to the Jackiw-Teitelboim (JT) gravity.We will discuss these two points of views in section 5.

1.3.Other motivations and developments

Thecoupling can have two possible signs.Depending on the convention,for one of the signs,the deformed spectrum become complex if the undeformed energy is large enough.This leads to possible break down of unitarity.We will call this sign of the coupling the‘badsign’1Sometimes it is also called the ‘wrong sign’.However,we want to stress that these names should not be taken as moral judgements.We love both signs equally..The other sign which leads to well behaved spectrum in the high energy limit is called the ‘good sign’.These two signs of the deformation parameter lead to very different physics in the UV.

Holography.For the bad sign,we cannot take the original energy spectrum to be too large,otherwise the deformed spectrum becomes complex.There is an interesting holographic dual for this sign proposed in [17].The proposal is that for pure gravity (that is,not including matter fields) thedeformation corresponds to putting a Dirichlet boundary condition in the bulk at finite radius.The ability to‘move into the bulk’usingdeformation is very interesting from AdS/CFT point of view and might shed some lights on some fundamental questions such as bulk locality.The relation betweendeformation and the cut-off geometry is further explored in [18-21].

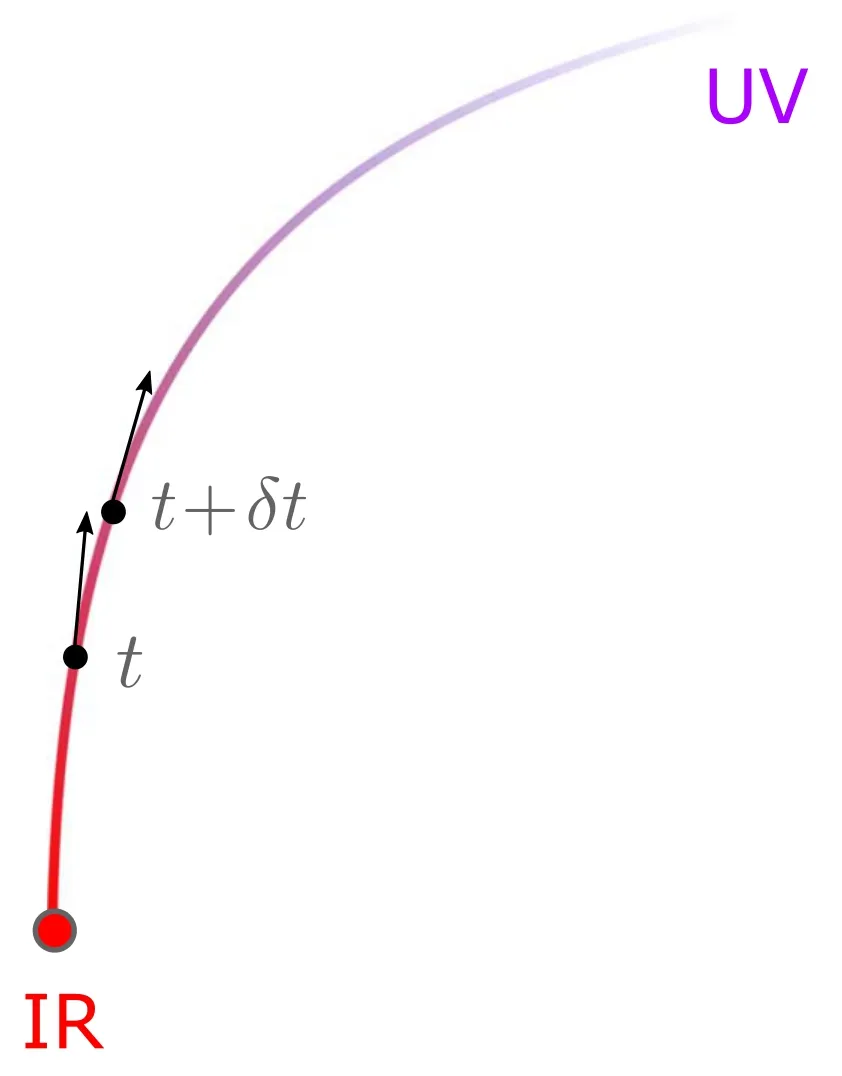
Figure 1.The flow in the space of 2D quantum field theories.The point t =0 corresponds to the undeformed IR theory.As we increaset,we go from IR to UV.

Little string theory.For the good sign,we can take the original energy to be infinitely high.One can investigate the density of states in the deep UV regime.It turns out the asymptotic growth of the density of states in thedeformed CFT interpolates between the Cardy behavior logand the Hagedorn behavior logρ～E.The Hagedorn behavior indicates that thedeformed theory is not a local QFT.In fact,this is the expected behavior for a class of non-local theories called little string theory which is dual to gravity theories on linear dilaton background.Motivated by this fact,a single trace deformation on the worldsheet of string theories inAdS3is proposed in [22].This deformation share many features of thedeformation.In particular,it gives the same deformed spectrum.This work is further developed in [23-26].In this review,we focus on the field theory side and will not discuss this interesting direction.For a complementary review,we refer to the lecture note of Giveon [27].

1.4.Structure of the review

This review is aimed for non-experts who want to learn about the subject for the first time,so we try to be very pedagogical,especially in sections 2-4.Most of the main results are derived in detail.In section 5,since we try to cover more topics,the derivations are more sketchy but we try to make the ideas and main steps clear.Finally in section 6,we briefly summarize new developments up to January 2021.This section is even more concise and it mainly serves as a literature guide for the interested reader.The structure of this review is as follows.

In the frist part,which consists sections 2 and 3,we first give the definition ofdeformation and derive the deformed Lagrangian for free massless boson.Then we consider the quantum theory and derive Zamolodchikov's factorization formula which is used to find the finite volume spectrum of the deformed theory on an infinite cylinder.In the last part,we present a different derivation of Zamolodchikov's factorization formula which does not rely on Cartesian coordinate systems.The formalism can be generalized to spacetimes with constant curvature and show that factorization formula does not apply for non-zero curvatures.

In section 4,we focus on the modular properties of the torus partition function ofanddeformed CFTs.We first prove that the torus partition function of thedeformed conformal field theory is still modular invariant.Then we show that by requiring modular invariance and that the deformed spectrum only depends on the undeformed energy and momentum of the same state,we can fix the deformation uniquely to be that of thedeformed CFTs.Finally we discuss some non-perturbative features of the deformed theory and new features of thedeformed CFTs.

In section 5,we first discuss Cardy's random geometry picture fordeformation.Then we discuss the 2D topological gravity point of view for thedeformation.Finally we discuss the holographic dual for the bad sign of the deformation parameter.

The topics discussed in the main part of this review are obviously limited.Moreover,is a quickly developing field,even for the topics we covered,new insights have been obtained in the past few years.To balance these points,we review briefly other topics and developments ofdeformation until January 2021 in section 6.

2.Definition and deformed Lagrangian

In this and the next section,we give the defniition of thedeformation of 2D QFTs in the Lagrangian formulation.In the current section,we discuss how to obtain the deformed classical Lagrangian for the free massless boson and show that the deformed Lagrangian is basically the Naumbu-Goto action in the static gauge.We then discuss the deformed spectrum on an infinite cylinder in section 3.It turns out that the deformed spectrum can be obtained exactly and non-perturbatively.Our discussions mainly follow the original works [1,2,12].In section 3.4,we give an alternative proof of the factorization formula without using any specific coordinate system.This method is generalizable to homogeneous symmetric spacetime with non-zero curvatures.We see from this analysis that flat spacetime is special and have particularly nice properties.In this section,we define thedeformation of 2D QFT in the Lagrangian formulation and consider a simple example which is the free massless boson in detail.

2.1.Definition

Abstractly a 2D QFT can be defined by a LagrangianL2For theories that cannot be described by a Lagrangian,there can be other ways to define this deformation.For example,for any CFT,the deformation can be described by the trace flow equation..We consider a trajectory in the field theory space parameterized by t and denote the Lagrangian at each point of the trajectory byL(t).The flow for theories on the trajectory is triggered by the operator det3We follow the sign convention of [2],which is different from [17].

This is depicted in figure 1.

To write down the results explicitly,let us fix some conventions.We work in two dimensional Cartesian coordinate(x,y).As usual we can define the holomorphic and antiholomorphic coordinatesz=(z,) by

The components of stress energy tensor in these two coordinates are related by

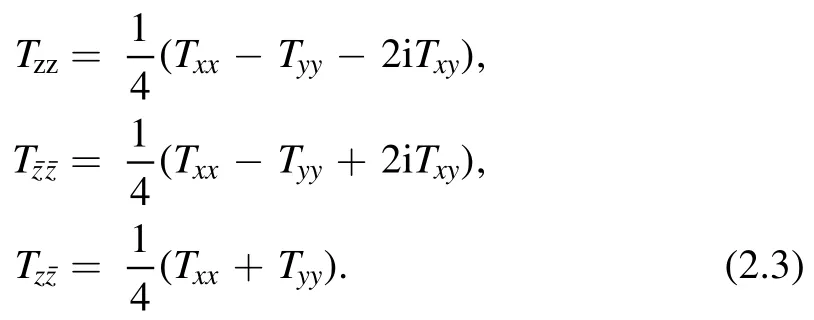
Following the conventions in [1,2,12],we define

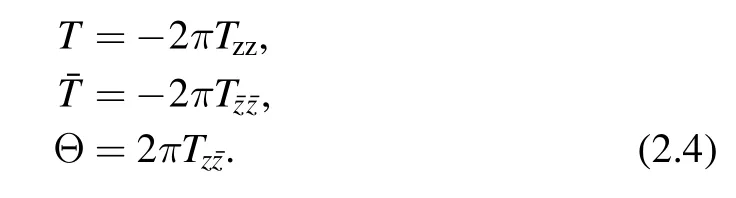
Then theoperator is given by

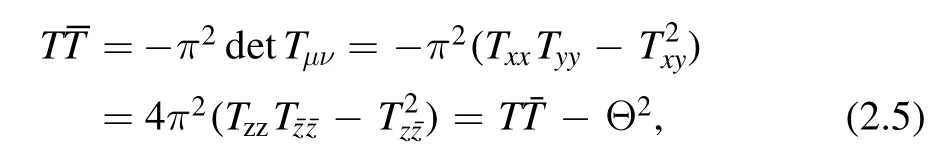
where we have used the relations in (2.3) and (2.4).We use the notationto denote the composite operator.This is different from the quantityin general.Theoperatoris of dimension [mass]4.Therefore the couplingt is of dimension [length]2.From RG point of view,this is an irrelevant deformation.

Since the operatoris a composite operator,we should ask how it is defined precisely.We will define it by point splitting and show that it is well-defined up to derivatives of other local operators.This will be discussed in more detail in section 3.

2.2.Deformed Lagrangian

The definition in (2.1) might seem a bit abstract,so let us work out an explicit example to get some feeling about it.We consider the simplest possible QFT,namely the free massless boson and see what the deformed Lagrangian looks like.This derivation is first presented in[2],which we also follow here.The Lagrangian is given by

where we have introduced the short-hand notation for the holomorphic and anti-holomorphic derivatives

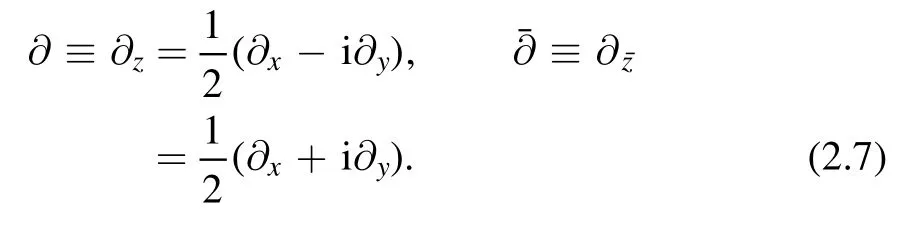
We will show that the deformed Lagrangian takes the following form

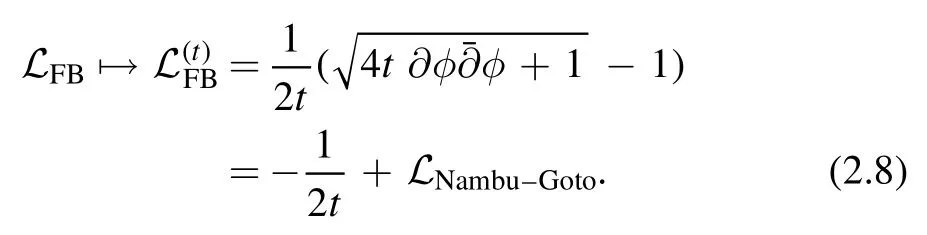
The square root part is exactly the Nambu-Goto action4This is part of the reason we follow the sign convention of [2],otherwise the NG action looks a bit strange with minus signs.in a three dimensional target space

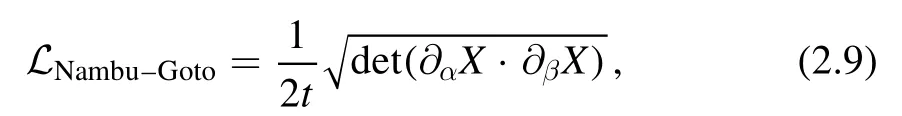
in a specific gauge called the static gauge5The static gauge is the gauge choice that one identifies two of the target space coordinates with the worldsheet coordinates.X1=x,

Now we start the derivation.To simplify the notation,let us introduce

Given the Lagrangian,the canonical stress-energy tensor is given by

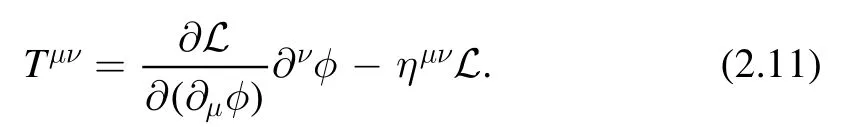
Written in terms of components,

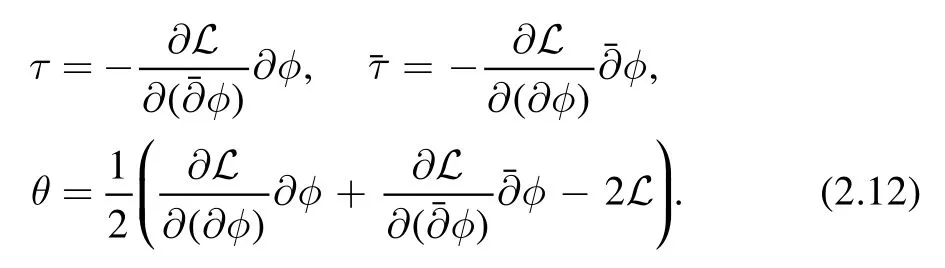
The key equation which allows us to find the deformed Lagrangian is the following

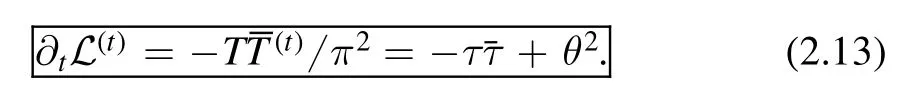
This equation comes directly from the definition of-deformation.Since the left hand side of(2.13) involves a derivative in t while the right hand side does not,we can perform a perturbative expansion in t and set up a recursion procedure to find the coefficients of the t-expansion order by order.To this end,let us write

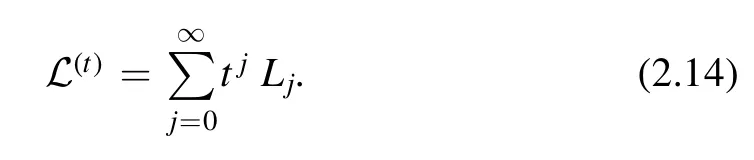
Using this ansatz,at the (j+ 1)th order of t (2.13) takes the form

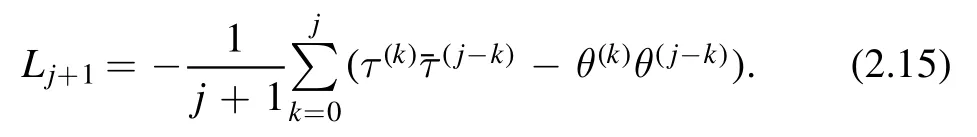
The main point here is that the right hand side only involvesτ(k),(k)andθ(k)withk≤j.These are determined by Lkas follows

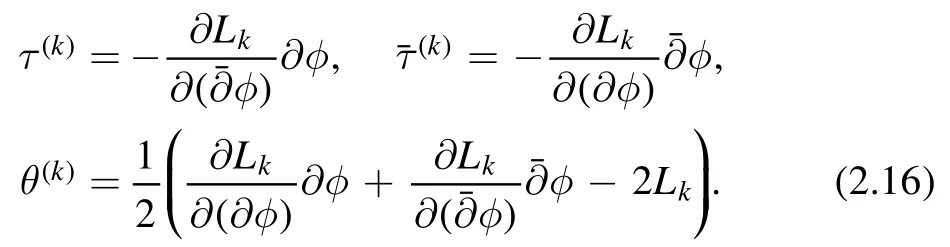
The initial conditions for the recursion relation is

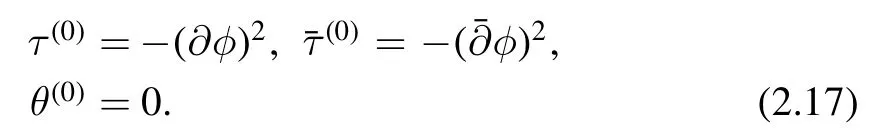
From these,we find the first coefficient L1from (2.15)

From L1,we can work outτ(1),(1)andθ(1)using (2.16)

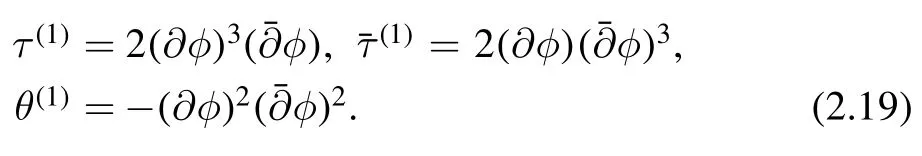
Then we can use again (2.15) to construct L2

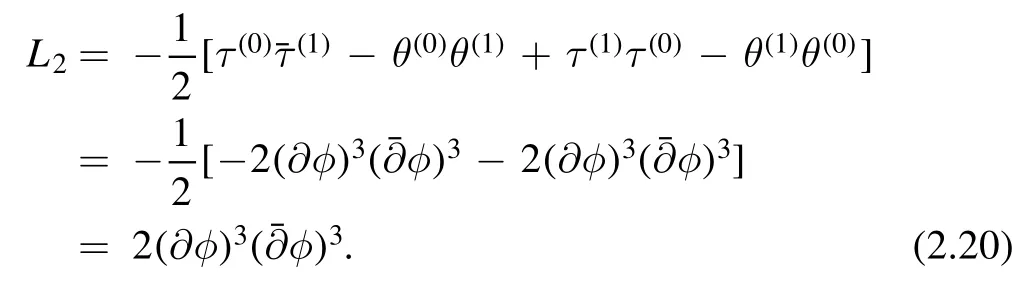
Having L2at hand,we can deriveτ(2),(2)andθ(2)using(2.16)again.Then we can obtain L3,and so on.Working out the first few orders,one can find a general pattern of Lj6This can be done for example using the‘FindSequenceFunction’of Mathematica.

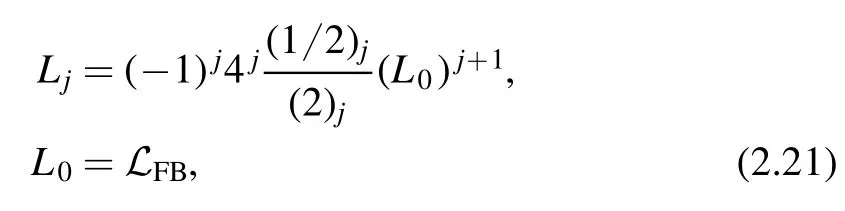
where(a)nis the Pochhammer symbol

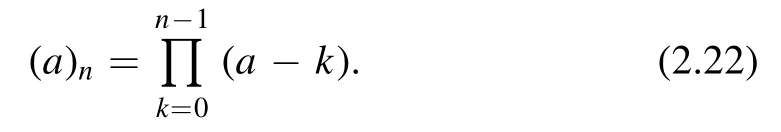
Plugging (2.21)-(2.14),one finds the deformed Lagrangian (2.8).

Alternatively,if it is hard to guess the closed form formula,one can proceed as follows.From the first few orders,we already gain some idea about what the Lagrangian looks like.Therefore we can make the following ansatz

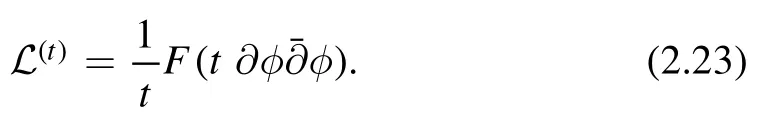
Using this ansatz,we can write the defining equation(2.13)as a differential equation ofF(x) whereIn more detail,we have

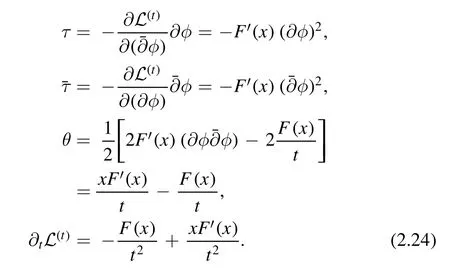
Plugging into (2.13),we obtain the following differential equation forF(x)

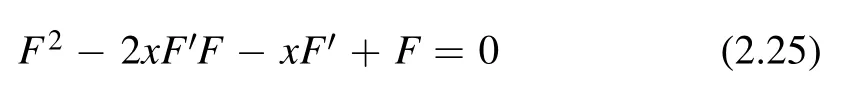
with the initial condition L(t=0)=we can easily solve this equation and find

This is exactly the Lagrangian we promised in (2.8).

Several comments are in order for the deformed Lagrangian.First of all,it is clear that similar strategy can be applied for more general Lagrangians,such as more fields and non-trivial potentials.This kind of computation has been performed in[2,10,18]and in general they lead to non-local Lagrangians.

It is well-known that the Nambu-Goto Lagrangian describes the propagation of a free bosonic string.We also see thatplays the role of string tension in the Lagrangian(2.8).Intuitively,when t = 0 we have a string with infinite tension which reduces to a point particle whose motion is described by a local Lagrangian.At finite t,we have some finite string tension and the Lagrangian describes some extended object.This is another hint of the non-local feature of the-deformed QFTs.

The classical Lagrangian gives some first taste of the deformed theory,but the quantization of such kind of Lagrangians are obviously hard.Even for the Nambu-Goto action,this is a non-trivial problem in the context of effective string theory(see for example[32]and references therein).In fact,it is not clear at the moment how can we make use of these Lagrangian in practice to compute some observable such as the spectrum or correlation functions.Conformal perturbation theory is not well-developed so far(see[18,112]for the first order calculation in conformal perturbation theory for certain correlation functions).The main problem is that as usual conformal perturbation theory leads to divergent integrals and a good prescription to regularize such integrals has not been fully worked out yet.

One final important remark is that despite of the difficulties we mentioned above,the deformed theory is solvable in the sense that if we know the undeformed spectrum,we can find the deformed spectrum explicitly.This will be the focus of section 3.

3.Deformed spectrum

In this section,we derive the deformed spectrum of thedeformed theories.Consider a QFT on an infinite cylinder with radius R.We denote the eigenstates of the Hamiltonian by ∣n〉 .The starting point for deriving the deformed spectrum is Zamolodchikov's factorization formula

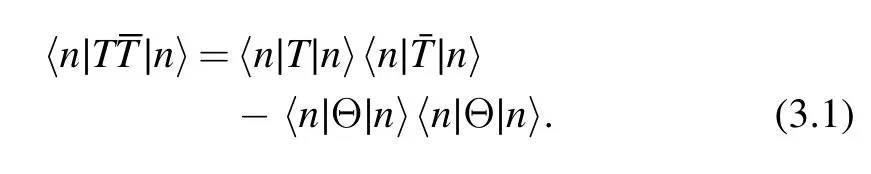
We want to address two issues in this section.Firstly,we need to explain more carefully how theoperator is defined by point splitting as we promised in the previous section.Secondly,we need to prove the key equation (3.1).

3.1.The operator

Let us start by defining theoperator.In the(z,) coordinate,the conservation of the stress-energy tensor∂μTμν=0 can be written as

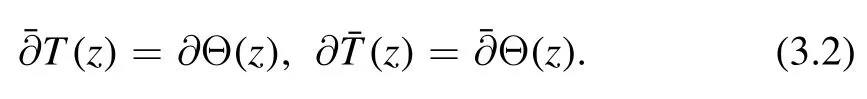
We define the operator by point splitting.Consider the following limit

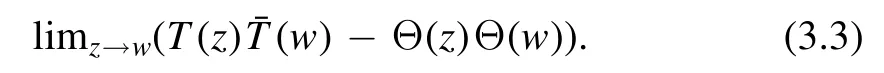
In general,taking this limit leads to divergences.We will prove that this operator is in fact well-defined up to derivatives.Why should one expect something special will happen for the specific combination (3.3)? To this end,we can consider the undeformed CFT.The trace of the stress-energy tensor vanishes for CFTs.The two-point function of the stress-energy tensor in d dimensions is given by

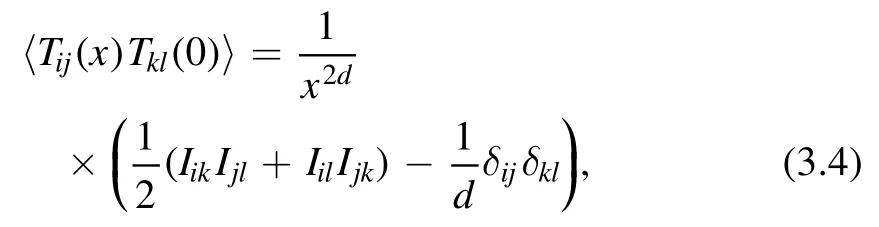
where

The specific combination in (3.3) is given by

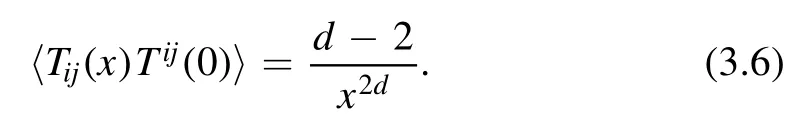
We see that when d = 2,the limitx→0 is well-defined.This is of course something we know already.In 2D CFT,the holomorphic and anti-holomorphic part of stress-energy tensor do not talk to each other and hence their OPE is regular.On the other hand,it also hints that at higher dimensions,things become more complicated,even for CFTs.

We will show that the limit in (3.3) is well-defined beyond CFT and along the wholedeformed trajectory where the trace Θ is no longer zero.The derivation below follows closely Zamolodchikov's original paper [12].Let us take the derivativeof (3.3)

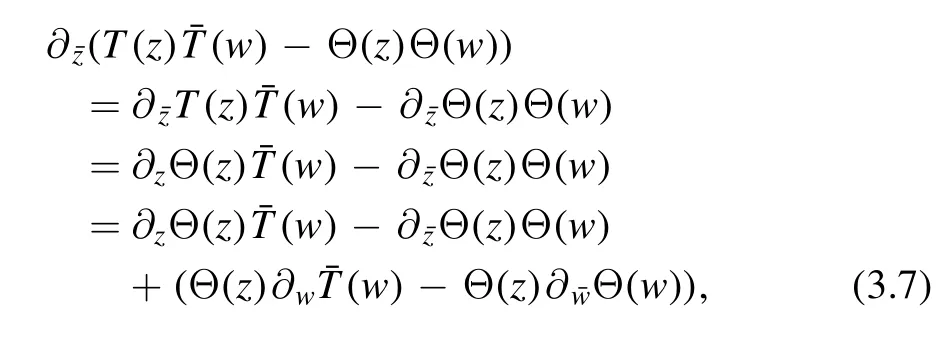
where in the second line we have used the conservation law(3.2).Also by the conservation law,the term we add in the bracket in the third line is in fact zero.The last line can be rewritten as

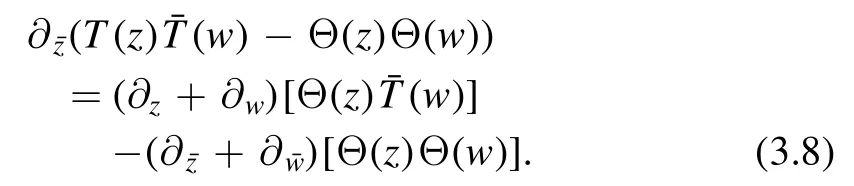
Similarly,we can find that

The reason of writing the results in the right hand side of(3.8)and (3.9) can be seen from OPE.For example,consider the OPE of Θ(z)T(w)

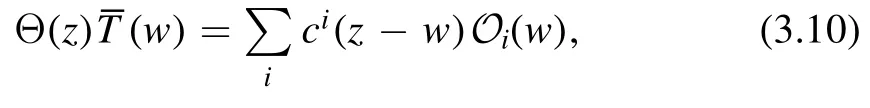
where the sum is over all operators in the spectrum.The formc i(z-w) is due to translational invariance.It is clear that (∂z+ ∂w) andannihilate the coefficientsc i(z-w),so it only acts on the operators.The conclusion is that

The exact form ofAi,,Di… are not important.The important point is that the operators that appear on the right hand side of(3.11)all takes the form of derivative of some operators.This gives a constraint for the form of OPE.Let us write the OPE as

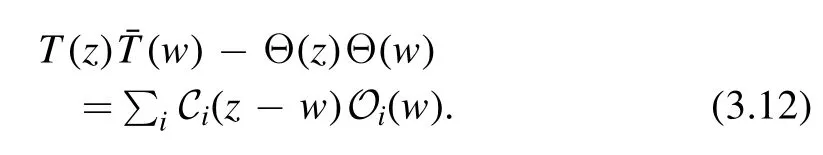
From the previous analysis,we can see that if an operatorOkis not the derivative of another operator,then the correspondingCi(z-w)must be a constant,i.e.does not depend on z or w.We prove this by contradiction.Suppose we have the termCn(z-w) On(w) in the OPE whereOnis not the derivative of another operator

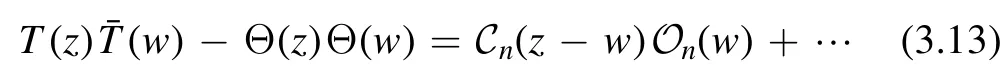
Taking derivative on both sides

Note that the first term is not compatible with the result(3.11)unless∂zCn(z-w)is zero,namelyCn(z-w)is a constant.If the operatorOnis already a derivative of some other operators,then the above form is compatible with the result (3.11)so we do not get additional constraints.Absorbing the constant coefficient into the definition of the local operator,we conclude that

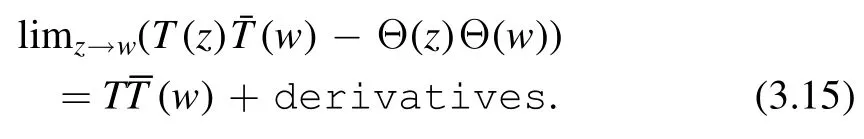
We see that the operator itself is defined up to total derivatives.However,when putting into the expectation value,the derivative terms vanish.This is because the expectation value is constant in a translational invariant theory.Taking derivatives leads to zero.

3.2.Factorization formula

Now we are ready to prove the main formula (3.1).As a first step,we want to prove that the following quantity

which looks like some two-point function is actually a constant.This can be proven as follows.Taking the derivativeofC(z,w),

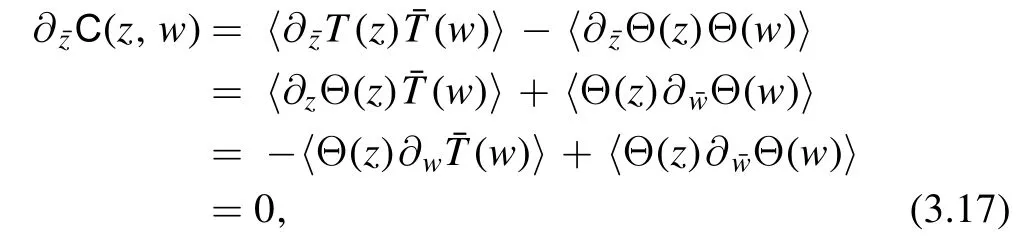
where we have used the conservation laws and the translational invariance to move the derivative from one operator to the other at the price of a minus sign.Similarly we can prove that∂zC(z,w) =0.HenceC is a constant.

Now thatC is a constant,we can write it in two different ways.Firstly,since we are on an infinite cylinder,we can take the two points infinitely separated from each other.In this limit,by clustering decomposition theorem,the two-point functions can be factorized and hence we find

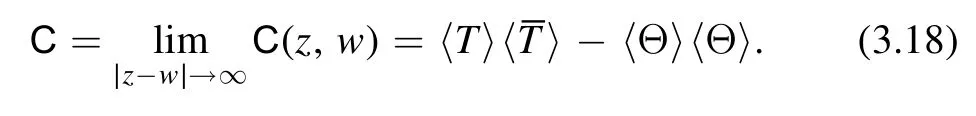
On the other hand,we can take the coinciding limit and keeping in mind that the derivative ambiguities vanish within the expectation value,we find that

Combining (3.18) and (3.19),we proved the factorization formula(3.1)for the vacuum state ∣n〉 = ∣0 〉.To complete the proof,we need to show that it holds for general excited state.Let us again define

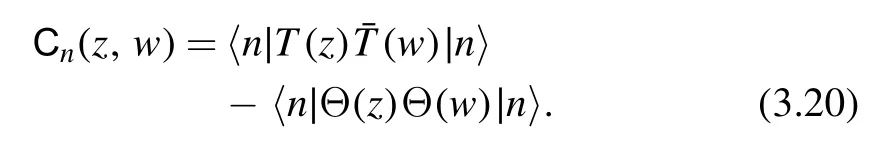
We can show thatnC is a constant as before.The difference between the vacuum state and excited states is that the asymptotic factorization property (3.18) no longer holds.There's a possibility to pick up contributions from intermediate states.This can be seen from the spectral expansion

and similar spectral expansion for〈n∣Θ (z) Θ (z′) ∣n〉.Note that in(3.21)we have written the exponential factors in Cartesian coordinatesz=(x,y).Now it is clear that forCnto be independent of the coordinates,all the terms with non-diagonal matrix elements should cancel between the two terms in(3.20).We are therefore left with diagonal matrix elements.Taking the limitz→z′ ,we obtain

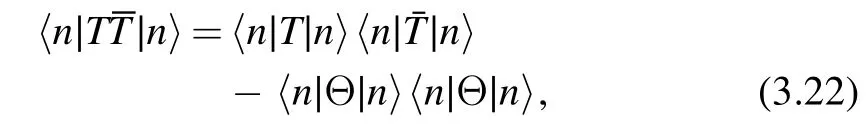
which is the key result we are after.

3.3.Burgers’ equation and deformed spectrum

The proof of the factorization formula only depends on Lorentz invariance and conservation of the stress energy tensor.Since both are still valid along theflow,we expect the factorization formula holds for the deformed theory at generic point t.Then we can use the factorization formula to find the spectrum of the deformed theory.This is done by translating factorization formula into a differential equation of the spectrum.For QFT on a cylinder of circumference R,expectation values of components of the stress-energy tensor are related to the spectrum as

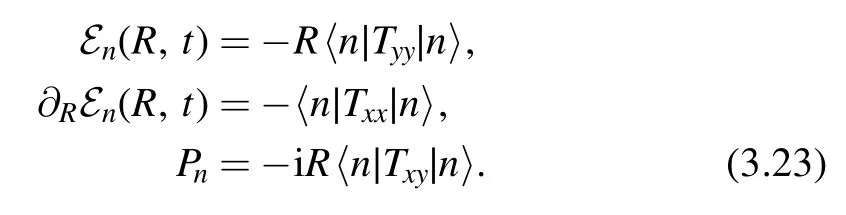
In this way,we can write the right hand side of the factorization formula(3.1)in terms ofEnand Pn.On the other hand,by the definition ofdeformation,we have

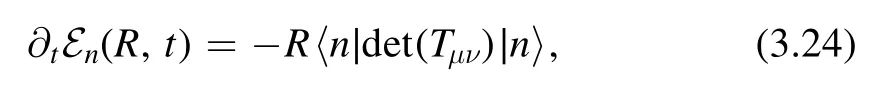
on the left hand side of the factorization formula.Combining these results,we find

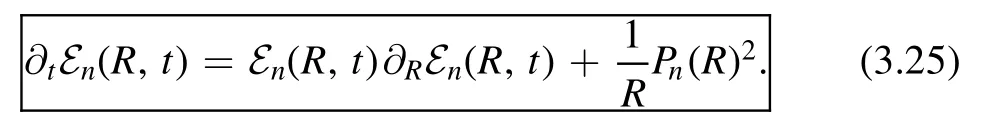
This is the inviscid Burgers’equation in one dimension.This equation is well-known in fluid mechanics which describes shock waves and can be solved by method of characteristics.To solve the equation,we need the initial condition En(R,0) =E n(R).This is particularly simple for CFTs since we have

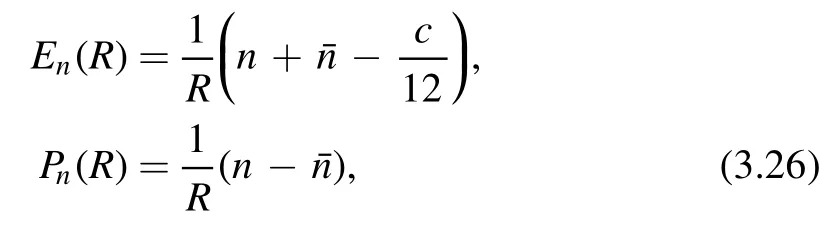
where n andare the eigenvalues of the Virasoro generator L0andWith the initial condition (3.26),the solution of Burgers’ equation is given by

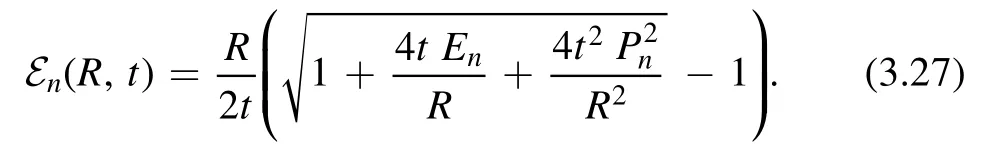
The momentum Pnare quantized and remain undeformed.Several comments are in order for the deformed spectrum.Firstly,if we do not impose the initial condition En(R,0) =En,we can find two solutions for the Burgers’equation corresponding to the two branches of square root

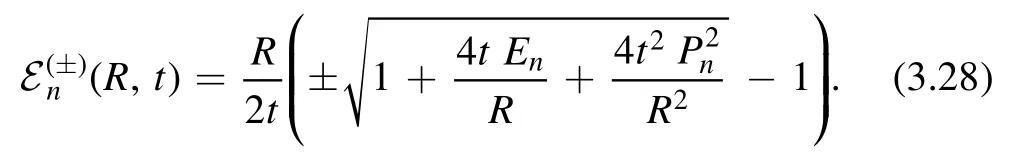
The equation (3.25) is a nonlinear partial differential equation.In fact it can be brought to a simpler form and written as an ordinary differential equation (ODE).Let us introduce the dimensionless quantities

We define the dimensionless coupling constant

where α is some multiplicative constant such aswhich we keep arbitrary for later convenience.Using this change of variable,the Burgers’ equation can be rewritten as an ODE

The solution of the Burgers’ equation or ODE takes the form of a square root,thereforeEn(λ) can be taken as the solution of the following quadratic algebraic equation

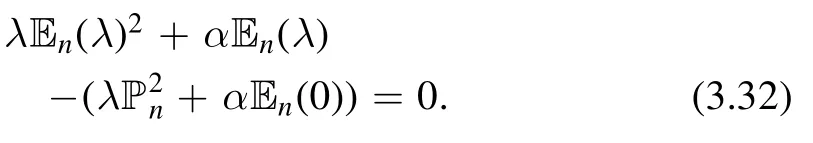
Or equivalently,

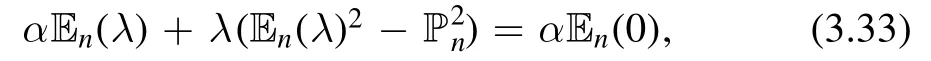
which states that the combinationis a constant along the flow.The right hand side is simply the value of this quantity at λ = 0.This quadratic equation actually has physical meaning in the string theory side.It corresponds to the mass-shell relation.The deformed spectrum for single trace deformation of string theory [22,27] is obtained from this algebraic equation instead of a differential equation.

Taking derivative with respect to λ on both sides of the quadratic equation,we find the ODE(3.31)again.Writing the ODE in terms of dimensionful quantities and translate the derivative of ′Enand ′E En nas derivatives with respect to t and R respectively,we recover the Burgers’ equation.

3.4.A covariant proof

The proof of factorization formula in the previous section uses the Cartesian coordinate system.Physical results should not depend on the choice of coordinate systems.We thus look for an alternative derivation of the factorization which does not depend on any specific choice of coordinate systems.To this end,it turns out to be helpful to be slightly more general and consider spacetimes with maximal symmetry,for example sphere and hyperbolic space.The idea is to exploit the symmetry of spacetime and write the two-point function of the stress energy tensor in a convenient form.We follow the discussions in [65].

3.4.1.An invariant biscalar.Recall that the central step towards the factorization formula is to prove that the quantity C(x,y) defined in (3.16) is a constant.This quantity can be written in the Cartesian coordinate as

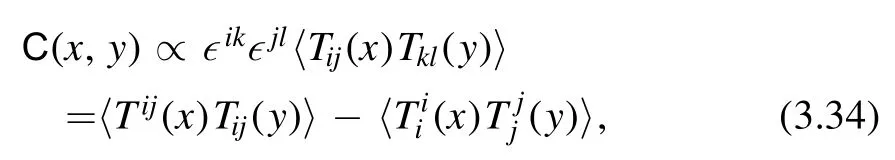
where we have used the identity∈ ik∈ jl=δ il δkj-δ ij δkl.An alternative proof thatC(x,y) is a constant is given in [13].Both proofs are done in the Cartesian coordinate.This fact should not depend on which coordinate system we are using.So we should first defineC(x,y) in a way which is invariant under change of coordinates.

Below we use Latin lettersi,j,… to denote indices of Cartesian system and Greek lettersμ,ν,…for those of general coordinate system.It is tempting to simply replacei,jbyμ,νin (3.34) and take it as a definition ofC(x,y) in general coordinate.However,this naive replacement does not work because we are contracting indices at different spacetime points.The resulting quantity is not invariant under coordinate transformation.Since the factors at different points do not cancel each other.We need some kind of‘connection’to make the two points talk to each other.In order to gain some idea,let us consider a similar situation in gauge theory.Suppose we want to make a gauge invariant bilinear in terms of two fermionsandψ(y) which transform as

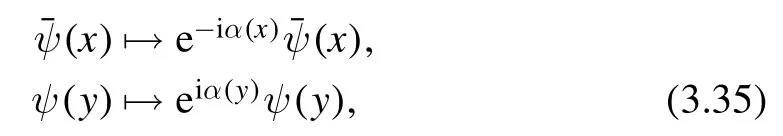
under gauge transformation.Simply taking)ψ(y) does not work because the two phase factors do not cancel.To make a gauge invariant quantity,we need a Wilson line to connect the two spacetime points.The following quantity

is gauge invariant.HereW(x,y) is the Wilson line

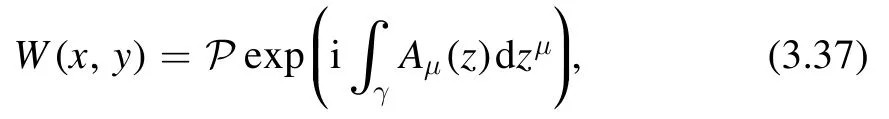
whereP denotes path ordering and γ is a path between the two spacetime points.

To define an invariant quantity C(x,y),we need a quantity similar to a Wilson line.In fact,such a quantity also exist in gravity theory and is called the parallel propagator.

Parallel propagator.We give a brief introduction to the parallel propagator following [33].Consider a pathγ:xμ(λ)parameterized by an affine parameter λ.The equation of parallel transport along this path is given by

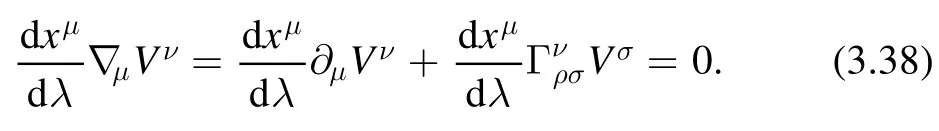
Solving the parallel transportation equation for the vectorVμamounts to finding a matrixsuch that it relates the values of the vectorVμat two different positionsλ0and λ

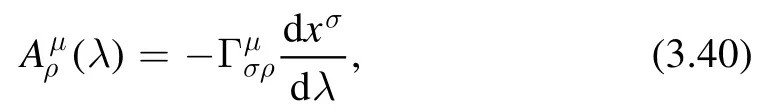
then the parallel transport equation (3.38) can be written as

Substituting (3.39) into (3.41),we obtain

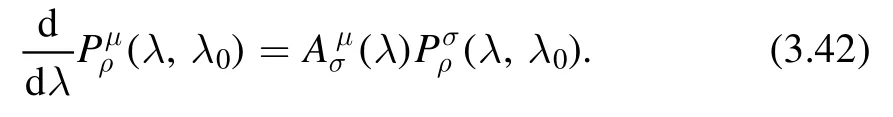
A formal solution of this equation is given by the following path-ordered exponential

The parallel propagator transforms as a bi-vector which connects two spacetime points.For more detailed introduction,we refer [33] and also [34,35].

The definition of the parallel propagator depends on the choice of the path.For our purpose,we choose the path between two points x and y to be the geodesic.We denote such parallel propagator asUsing parallel propagators,we propose that the invariant biscalarC(x,y) can be defined as

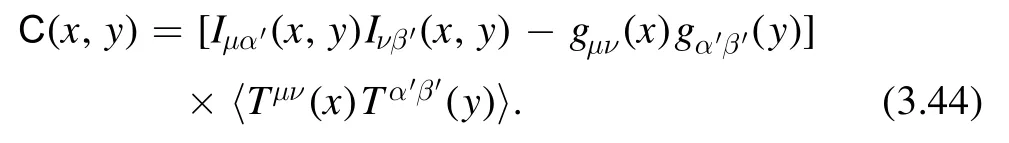
3.4.2.Maximally symmetric bi-tensors.In a maximally symmetric spacetime,two-point function of two scalar operatorsO1(x) andO2(y) is a function of the geodesic distance between the two pointsθ(x,y),namely

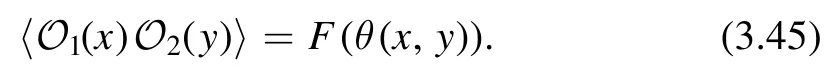
On flat spacetime this reduces to the familiar result that〈O1(x) O2(y) 〉 =F(x-y).(3.45) has a non-trivial generalization to two-point functions of symmetric tensors of arbitrary rank.The statement is that the two-point functioncan be decomposed into different tensor structures.All the tensor structures are constructed in terms of the vectorsnμ,mα′,the metricgμ ν,gα′β′and the parallel propagatorIμα′.Here the vectorsμnandmα′are derivatives of the geodesic distance

where indices with a prime (∇α′) means we take derivatives with respect to the coordinate at the second positionx′ .These two vectors are normalized asnμ nμ=m α′mα′=1 and are related by the parallel propagator as

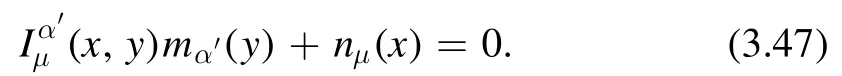
The proof can be found in the paper [34,35].For the stressenergy tensor,we have the following tensor decomposition

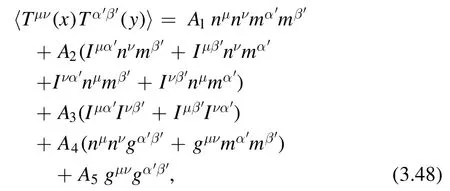
whereAi(θ) (i=1,…,5)are scalar functions that only depend on θ.In what follows,we will need the covariant derivatives of the quantitiesIμα′,μnandmα′which are [34]

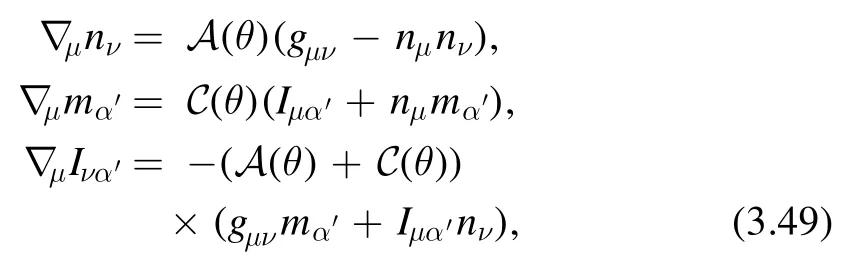
whereA(θ) andC(θ) are scalar functions of the geodesic distanceθ(x,x′).For different spacetime,they are given by

· Flat spacetime

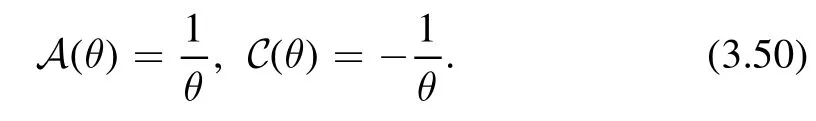
· Positive curvature spacetime (scalar curvature R=d(d-1) /R2)

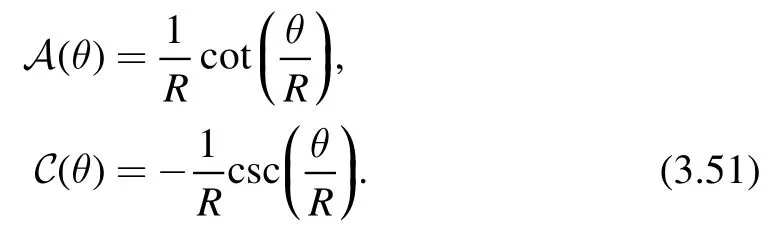
· Negative curvature spacetime (scalar curvature R = -d(d-1) /R2)

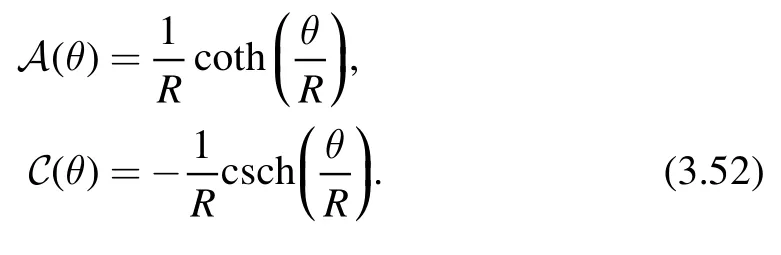
Using the decomposition (3.48) and the definition (3.44),we can write the invariant biscalarC(x,y) in terms ofAi(θ)

where d is the dimension of the spacetime.For d = 2,we simply have

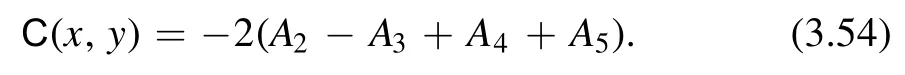
To prove the factorization formula,we need to show that∂μC(x,y) =0.To this end,we need to take into account the conservation law of the stress energy tensor.

3.4.3.Ward identity and factorization.The five unfixed coefficientsAi(θ) are not independent.They are related to each other by the Ward identity

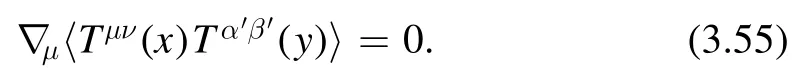
We act ∇μon the right hand side of(3.48)and then make use of the relations (3.49).The result can be written as

Since the three tensor structures are independent,this is equivalent to three equations X = 0,Y = 0,Z =0 where X,Y and Z are given by

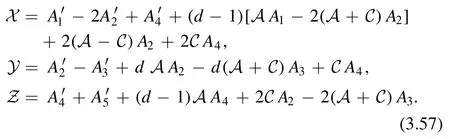
For d = 2,these become

Now we take the derivative ofC(x,y) defined in (3.54).We have

It is interesting to notice that the equation Y + Z =0 leads to

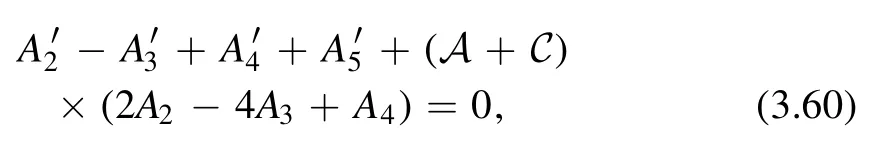
which allows us to get rid of the derivatives in (3.59)completely and we have

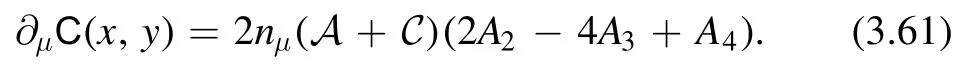
In flat spacetime,we have A + C =0 from (3.50) so that∂μC(x,y) =0.For curved spacetime,however,we have A + C ≠0.For example,

for the sphere.This shows that flat spacetime is special and the fact thatC(x,y) is a constant depends crucially on the flatness of spacetime.

In order to prove∂μC(x,y) =0in flat spacetime,our machinery seems a bit heavy compare to the previous proofs.However,the merit of this approach is that it can be easily to generalized to curved spacetime.We see that the invariant biscalarC(x,y) is no longer a constant in curved spacetime.In fact,one can do better and derive an explicit formula for the expectation value of theoperator in maximally symmetric curved spacetime.The conclusion is that the factorization formula does not apply,unless in the large-c limit.There are corrections to the factorization formula at finite curvature and central charge.For more details,we refer to [65].

4.Modular bootstrap and uniqueness

In this section,we study the torus partition sum of thedeformed conformal field theory.We are particularly interested in the modular property of the torus partition sum.More specifically,we ask the following two questions.

Firstly,as is well known,torus partition sum of 2D conformal field theory is modular invariant.After turning on thedeformation,we know the deformed spectrum.A natural question is what happens to the modular property of the deformed partition sum.The answer turns out to be that the deformed partition function is still modular invariant.This is a very nice property and again shows the internal simplicity of thedeformation.In addition,we can use this property to derive a Cardy like formula for the asymptotic density of states fordeformed CFTs.

To introduce the second question,we can take a slightly more general point of view.In fact,constructing solvable deformations in the Hamiltonian formulation is easy and one can construct infinitely many such deformations.Of course,not all of these deformations are physical.To constraint the‘physical’ ones,we need to impose some consistency conditions.One natural condition is requiring the torus partition sum of the deformed theory to be modular invariant.This resembles the idea of bootstrap.On general grounds,we expect that the consistency conditions will lead to some constraints of the infinite many deformations and select a subset of these theories.Our second question is how constraining is the requirement of modular invariance?Somewhat surprisingly,the constraint turns out to be so strong that it restricts the infinite family to a single theory.What's more,this theory is exactly thedeformed conformal field theory!We call this property uniqueness.

4.1.Modular invariance of torus partition sum

In this section,we investigate the first question.Namely,what is the modular property of thedeformed conformal field theory.

4.1.1.The set-up.Consider a CFT on a torus.The partition function of the CFT is given by

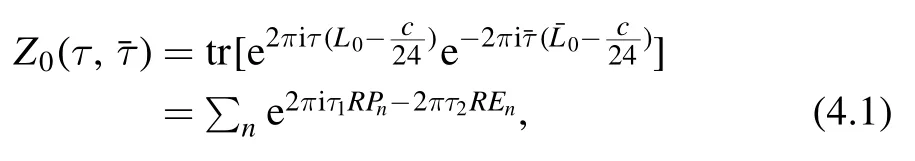
whereτ=τ1+ iτ2is the modular parameter that specifies the torus and=τ1- iτ2.The energy and momentum are given by

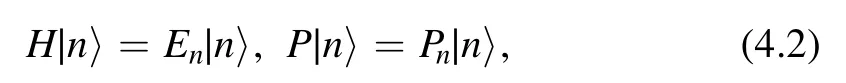
where

The CFT torus partition sum is modular invariant

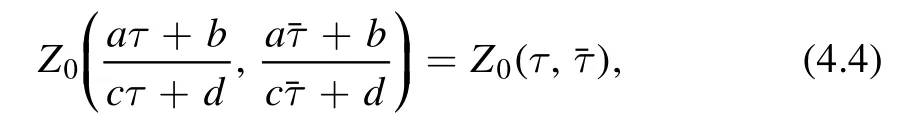
wherea,b,c,d∈ℤandad-bc=1.Modular invariance comes from a seemingly trivial observation.A torus can be identified with a lattice of the plane.The lattice can be parameterized by the complex parameter τ.However,this parametrization is not unique.Any PSL (2,ℤ) (modular)transformation on τ leads to the same lattice and hence the same torus.Physical results should not depend on how we parameterize the torus.This is the statement of modular invariance.

4.1.2.Deformed partition function.Now we consider thedeformation.We consider the spectrum on a cylinder of circumference R.The deformed energy has been derived in section 3

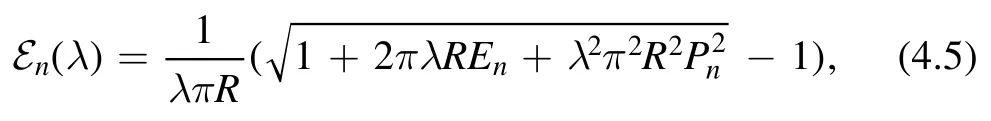
where we have introduced the dimensionless parameterλ=2t(πR2).The deformed partition sum is defined as

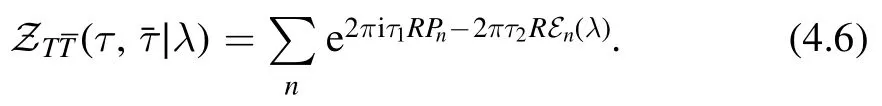
In order to study the modular properties of the partition sum,we can perform the perturbative expansion ofin λ

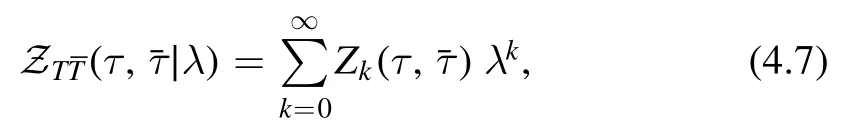
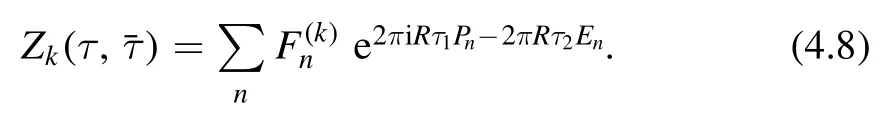
It is easy to see that inserting monomials of Enand Pnin the sum like (4.8) can be achieved by taking derivatives of the undeformed partition function (4.1) with respect toτ1andτ2.By this we simply mean,for example,

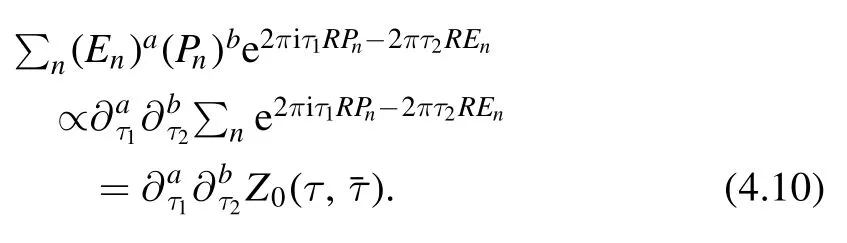
Notice that we can do this because the deformation of the energy spectrum is universal,namely all the energy levels are deformed in the same way.Using the replacement rule

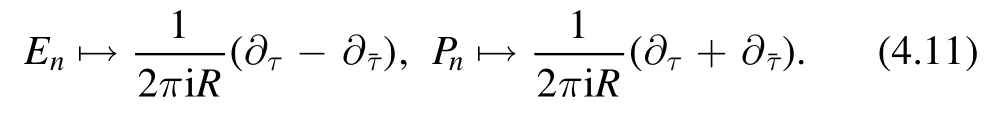
We can rewrite

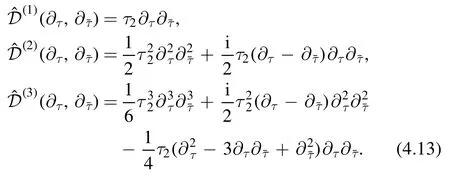
In what follows,we will study these differential operators in more detail.It turns out that these operators can be organized in a nice way which make it manifest thattransforms as modular form of weight(k,k).To this end,we will need some mathematics about the modular forms which we will introduce in the next subsection.

4.1.3.Some mathematics.A functionis called a modular form of weightif it satisfies the following property

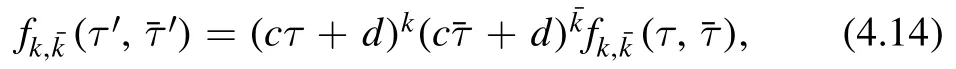
where

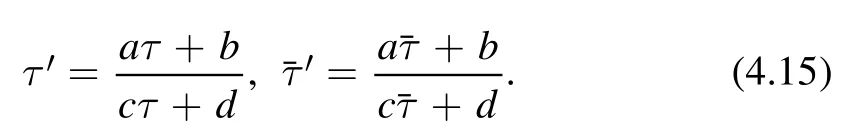
One simple and useful example isτ2= Imτ.Computing the imaginary part of (aτ+b)/ (cτ+d),we find thatτ2transforms as

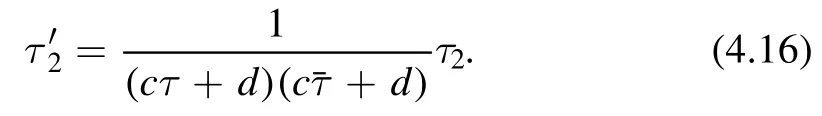
So we can say thatτ2is a modular form of weight (- 1,-1).Usually the derivative of a modular form is no longer a modular form,but becomes quasi-modular.Let us considerActing ∂τon both sides of (4.14) and using the factwe obtain

Or equivalently,

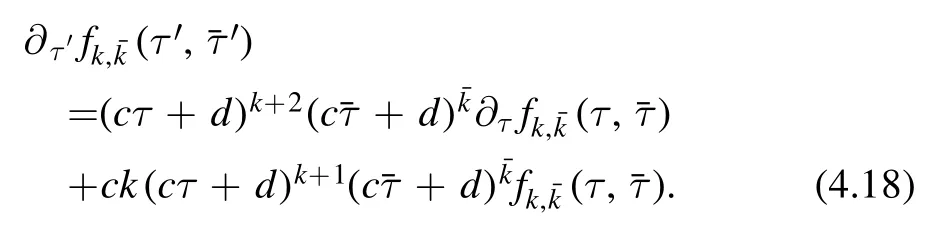
The first term is covariant,but the second term is anomalous.

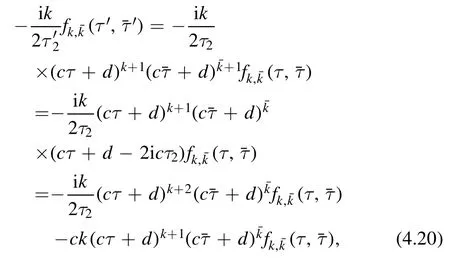
where in the second line we used the simple fact that

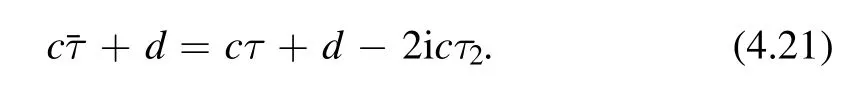
Taking the sum of (4.18) and (4.20),we see that the anomalous terms cancel each other exactly and we obtain

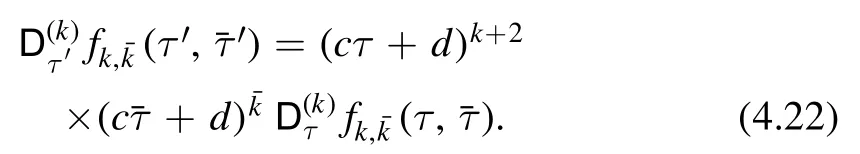
Therefore we have proved thatis a modular form of weightSimilarly,we can define the antiholomorphic covariant derivative

Acting this covariant derivative on a modular form of weightwe obtain a modular form ofNotice that the definition ofanddepend on the weights of the modular form that they act on.

The covariant derivativesandare called Maass-Shimura derivatives.Using these,we can define the following operators which are useful later

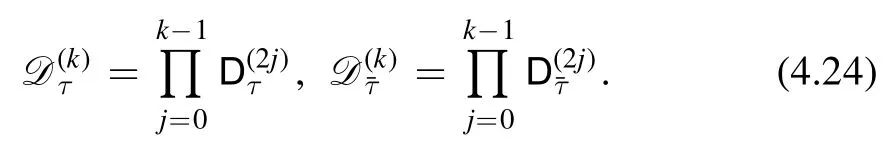
From the definition of these operators,it is easy to see that the operatortakes a modular form of weight(0,m) to a modular form of weight(2k,m) for any m.Similarly,takes a modular form of weight(m,0) to a modular form of(m,2k) for any m.

Notice that in the definition of the differential operators in (4.24),the operators on the left actually act on the ones to the right since the latter containSo if we expand explicitly in terms of ∂τand,the result is more complicated.As an example,let us write explicitly

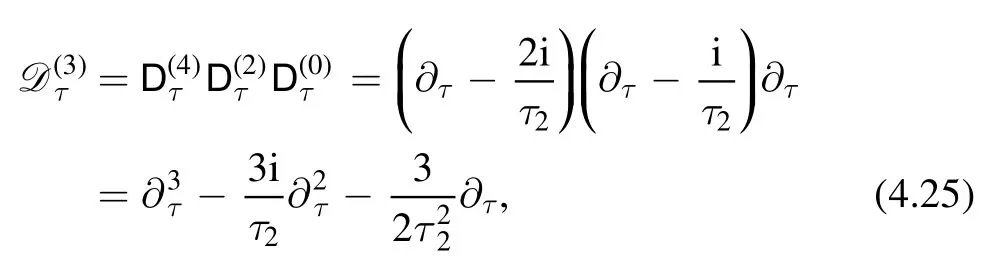
where we have used the fact that

4.1.4.Modular invariance of deformed partition function.Now we are equipped with necessary mathematical tools,we start to investigate the modular properties ofZk(τ,).We find that the first few differential operators given in(4.13)can be written in terms of the covariant operators defined in(4.24)in a surprisingly simple way

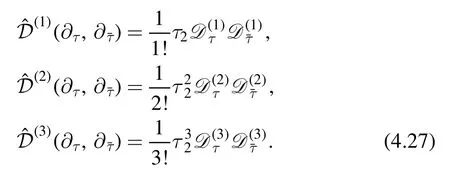
We can check further and find that to very high orders of k we have

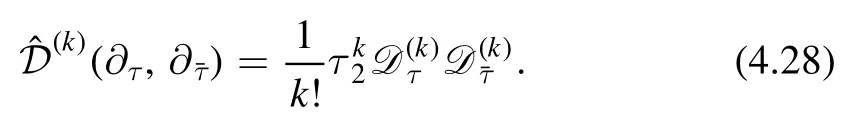
Again we emphasis that the differential operators on the left act non-trivially on the ones on the right.From the modular properties of the operatorsand,we see thattakes a modular function(which is a modular form of weight(0,0)to a modular form of weight(2k,2k)).Multiplying with,which reduces the weights by (-k-,k),we find thatmaps a modular function to a modular form of weight(k,k).If we require the dimensionless parameter λ transforms as a (- 1,-1) form,thenis invariant under modular transformation.This is of course a strong hint that the deformed partition function is modular invariant,but not yet a rigorous proof.To complete the proof,we can use the flow equation for the deformed partition function.This can be derived from Cardy's random geometry point of view,as we will discuss in section 5.In fact it can also be derived directly from the Burgers’ equation,as we will show now.

Flow equation.Let us first write the deformed partition function in terms of dimensionless quantitiesEn,Pnand λ

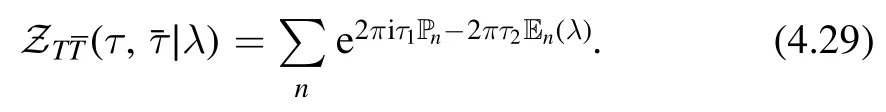
We quote the ODE (3.31) which is equivalent to Burgers’equation for CFTs (taking α = 1/π)

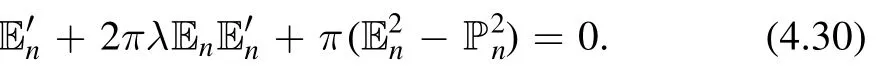
We can take derivative of the deformed partition function with respect toτ1,τ2and λ.These derivatives will act on the exponent and bring down some factors.For example,taking derivative with respect to λ,we have

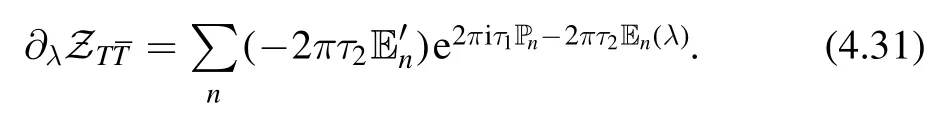
We can denote this relation by the replacement rule

Or equivalently,we write

Taking again the derivative with respect toτ2,we obtain the replacement rule

Combining (4.32) and (4.34),we have

Finally,it is easy to see that

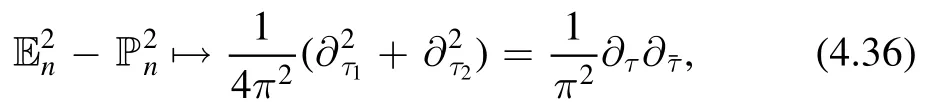
where we have used the relation

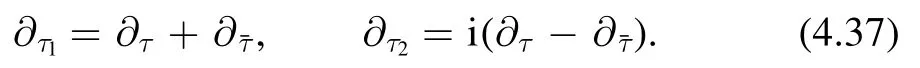
Now we can use the replacement rule to rewrite the ODE(4.30) as

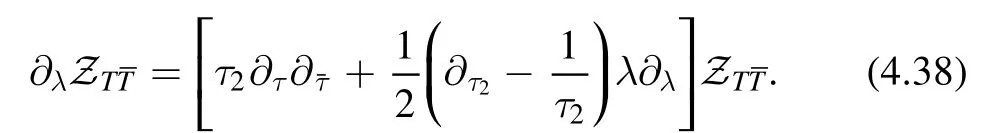
This is the flow equation we need.

A recursion relation.Now we plug the perturbative expansion of the partition function

into the flow equation (4.38),we obtain a recursion relation between Zpand Zp+1

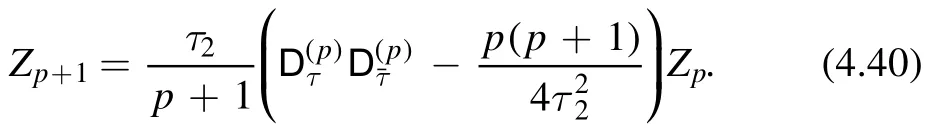
From this recursion relation,it is clear that if Zpis a modular form of weight(p,p),then Zp+1is a modular form of weight(p+ 1,p+1).By requiring that λ transforms as

we see that thedeformed partition function is modular invariant

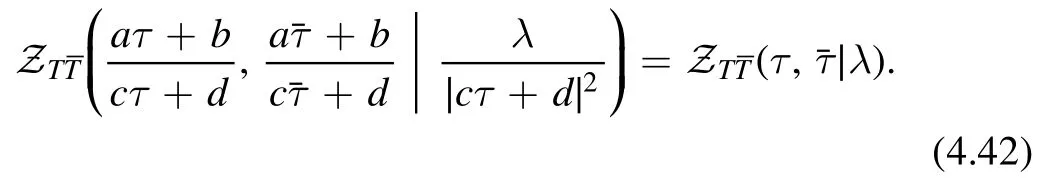
We notice that the quantization radius R also transforms under modular transformation as

Therefore the transformation rule forcomes solely from the transformations of R.If we write the deformed partition function in terms of the dimensionful parameter t,we have

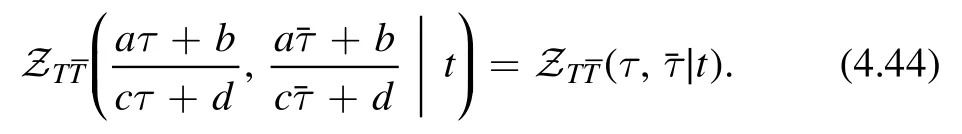
4.2.Modular bootstrap

Now we move to the second question.We consider the same setup as in the previous section.Let us forget about thedeformation for the moment and recover it from modular bootstrap.

4.2.1.Solvable deformations.For a given CFT on a cylinder of radius R,we can consider a trivially solvable deformation,depending on a dimensionless parameter λ

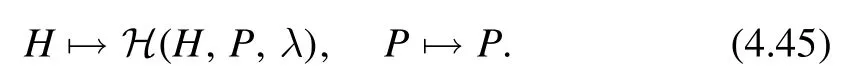
It is clear that the state ∣n〉 automatically diagonalize the deformed HamiltonianH

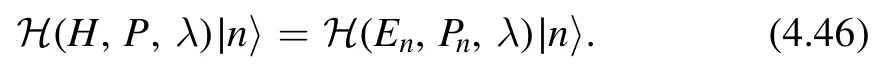
The momentum is not deformed.Let us denoteEn(λ)=H(En,Pn,λ) and the initial condition isEn(0) =En.We define the deformed torus partition function as

There are infinitely many possible choices for the function H(E,P,λ),but not all the deformations are physical.To restrict to a subset family of the solvable deformations,we need to impose some consistency conditions.One natural consistency condition for partition function on the torus is modular invariance.Let us impose that and see which kinds of theories do we get.More explicitly,we require

We will see that this condition is strong enough to fix the function H(E,P,λ)completely.Before that,let us make one comment here.One might ask that why should we require that λ transforms as in (4.48),can we instead require that λ transforms as a(m,n) form

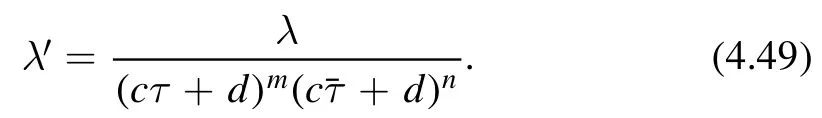
The answer is no.One can show that the only non-trivial deformations that is compatible with modular invariance is(m,n) =(1 ,1).This will be clear after our proof of uniqueness.

4.2.2.Perturbative expansion.We need to make another assumption for the deformed spectrum.We assume that the deformed energyEn(λ) has a regular Taylor expansion in λ

where Z0is the undeformed partition function.It is easy to work out the first few orders

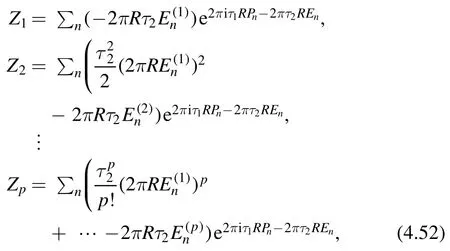
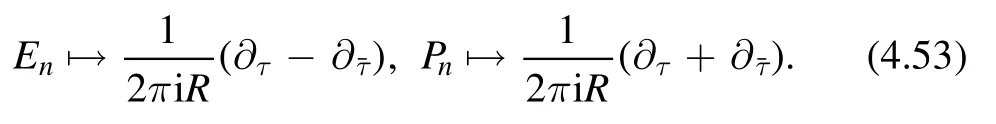
The Taylor coefficients Zpcan be written in terms of acting certain differential operator on Z0.They have the following structure

1.The differential operator is a polynomial in terms ofτ2

2.The highest order term ofτ2is given byTherefore from (4.54),we see thatis fixed by.Notice thatfixes Z1completely.

3.The lowest order term ofτ2is given byτ2(-2πR)Notice thatis the only quantity that does not appear in lower ordersZ0,Z1,…,Zp-1.

4.There are no terms withsuch thatm≤ 0.

Let us first notice that due to our assumption of the modular property (4.48),the Taylor coefficient Zptransforms as a modular form of weight(p,p)

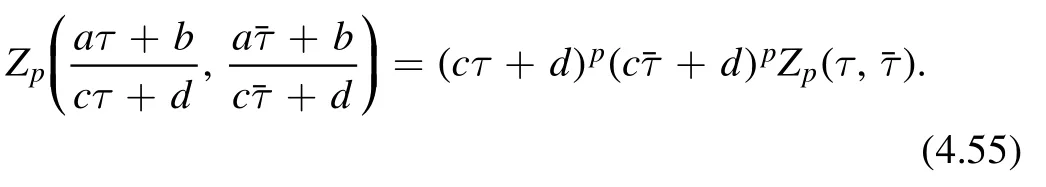
Our proof involves two steps

1.Uniqueness.Show that all Zpare uniquely determined

by the modular property.

2.Existence.Give a method to construct Zpexplicitly.

4.2.3.Uniqueness.We shall prove uniqueness by induction.First consider Z1

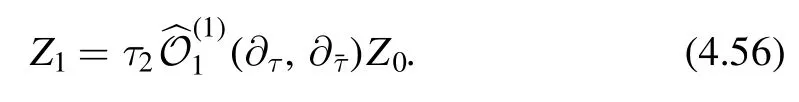
From our assumption,Z1is a (1,1) modular form.Thereforeis an operator which takes a(0,0)form to (2,2)form.It is not hard to see that the only possibility foris that

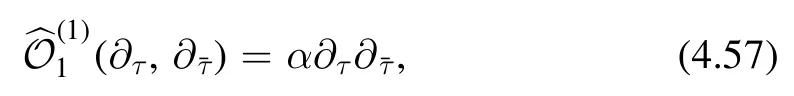
where α is an unimportant multiplicative constant that can be absorbed into the coupling constant λ.Now we consider the induction.AssumingZ0,Z1,…,Z pare completely fixed,we want to show that Zp+1is also fixed.As we discussed before,fixingZ0,…,Z pimply that we have completely fixed the energy shiftswithj=1,2,…,p.Then in the expression of Zp+1,the only unknown operator isthat couples toτ2.

Suppose two such operators exist,which we denote byandThen there are two quantities Zp+1andwhich are (p+ 1,p+1) forms Their difference

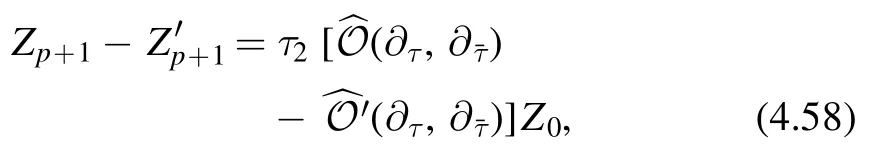
is also a (p+ 1,p+1)form.Notice that higher order terms inτ2cancel because they are fixed byThis implies that there must be an operatorsuch that

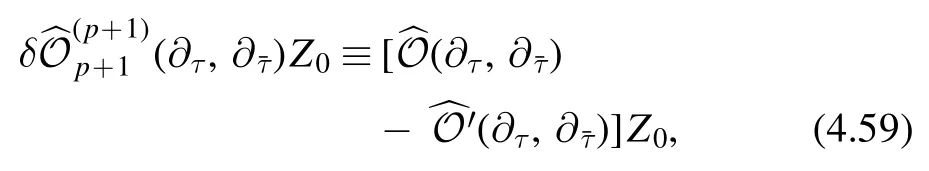
is a (p+ 2,p+2)form.We will show that such an operator does not exist forp＞0.Notice thatis a differential operator involving only the derivatives ∂τandand some numerical coefficients.It does not involves other modular quantities such asτ2.Let us analyze the action of ∂τandon a modular form of(k,).Using the covariant derivatives we have the following

The two terms on the right hand side are modular forms of weightsandSimilarly,actingleads to modular forms of weightandThe total increase of the weights are 2.To obtain the desired form,we need to act a total p + 2 derivatives of ∂τandHowever,apart from the wanted terms,we will also generate many unwanted terms along the way which we cannot get rid of in general.

As an example,consider p = 1.Suppose we want to generate a (3,3) form from (0,0) form by acting some operators made of ∂τand.The total weight is 3 + 3 = 6.There are four operators which generate such total weight:andThese operators generate the following modular forms

To generate the desired (3,3) modular form,we need to actandon Z0.However,these operators also generate the unwanted modular forms of weights (4 ,2) ,(5 ,1) and(2 ,4) ,(1 ,5).To cancel these unwanted modular forms,we need to take into account the operatorsandHowever,these operators will then generate the unwanted modular forms of weights (6,0)and (0,6),which cannot get canceled.Therefore there is no way to get rid of all the unwanted terms Similar analysis can be performed for modular forms of of weight(p,p) forp＞ 3.To conclude,there is no differential operator O (∂τ,)made of ∂τandthat takes a(0,0)form to a(p,p) form forp≥ 3.As a result,there cannot be two differential operatorsandSo the operatoris unique.This implies that Zp+1is uniquely fixed.

4.2.4.Existence.We have shown that the differential operator which leads to Zpis unique.The next step is to give an explicit way to construct such an operator.Of course,since we have proved thatdeformed CFT satisfies the modular invariance.By the uniqueness,the theory is nothing but thedeformed CFT.Suppose we do not know the deformed spectrum,can we still have a practical way to construct such a differential operator? This kind of construction will be useful for more general cases.

A covariant ansatz.Let us take a closer look at the following expression

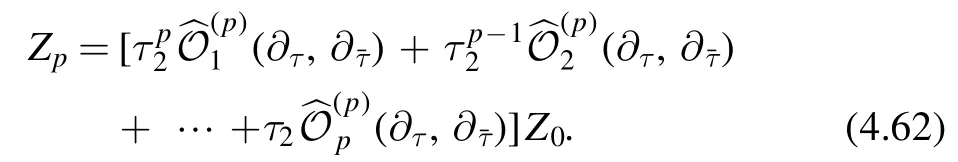
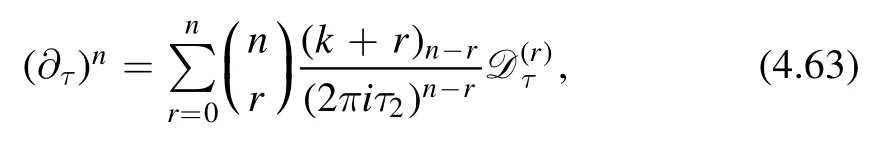
where(a)mis the Pochhammer symbol.A similar expression exists forThis implies that we can equivalently express the differential operator in terms ofandandτ2.Therefore we can write the operator in terms of linear combinations ofThe advantage of this rewriting is that each term increases the modular weight by a definite amount.For example,the operatoracting on a modular function leads to a modular form of weight(2i-k,2j-k).At each order p,we want Zpto be modular form of weight(p,p).We can make an ansatz so that each term in the ansatz leads to the desired weight of the modular form.We have

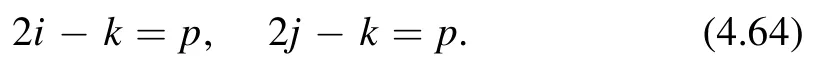
We see therefore i = j,so the ansatz consists of operatorsfor any integer i.In addition,the possible values of i are bounded from the structure of perturbative expansion (4.62).

· It is clear thati≥ 0 since negative numbers ofdo not make sense here.

· From(4.62),it is clear that the highest power ofτ2for ZpisThere are also factors ofτ2in the covariant derivativesbut they are all negative powers.Therefore we have 2i-p≤p,which impliesi≤p.

To sum up,the possible range of values of i is given by 0 ≤i≤pandi∈Z.Therefore at each order p,we can make the following ansatz

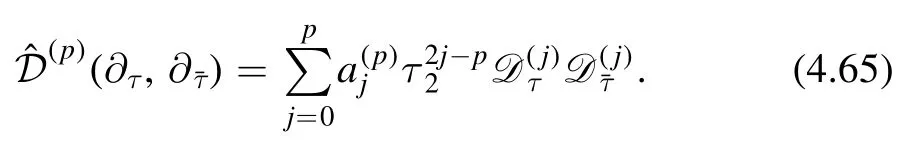
This ansatz has used the modular property of Zp.Now we need to fix the coefficients.These coefficients are fixed by the structure of perturbative expansion.Firstly,we notice thatis completely fixed becauseis always coupled toandis already fixed by Z1to be

where α is some constant that can be absorbed in the dimensionless coupling constant.We have

Expanding the covariant derivatives,we find

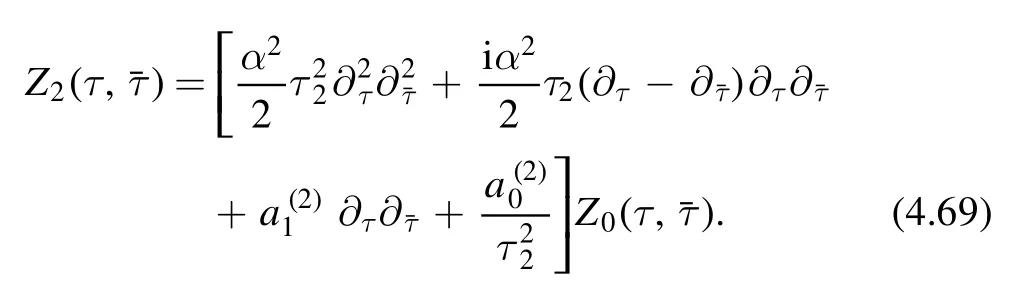
It is clear that the last two terms in (4.69) couple to nonpositive powers ofτ2and are not compatible with the structure of perturbative expansion.Therefore the coefficients need to be put to zero.We thus find

and fixZ2(τ,) to be

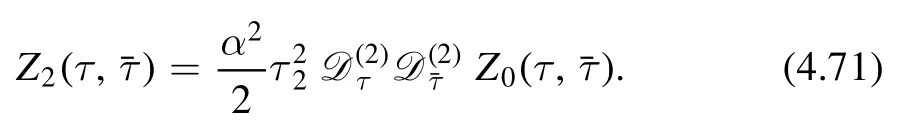
Similarly,one can find a few more terms This gives a systematic way to constructZp(τ,).In order to fix all the Zponce and for all,it is helpful to set up a recursion relation between Zpand Zp+1.From our previous analysis,we see that we need an operator which maps a(p,p) modular form to a(p+ 1,p+1) modular form.There are only two natural candidatesandTherefore we can make the following ansatz for the recursion relation

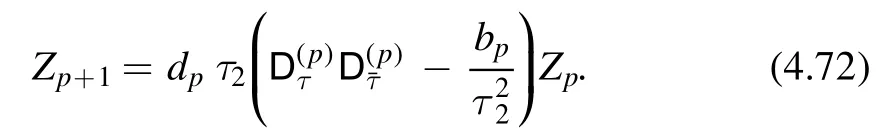
The coefficient bpcan be fixed by requiring that there is no terms at orderMore explicitly,we notice thathas the following expansion

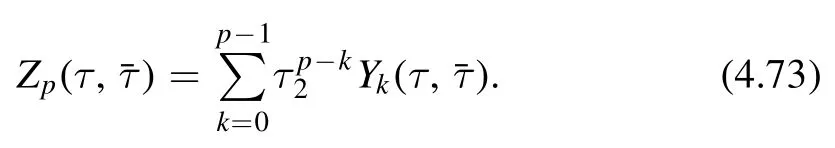
Acting the operator(4.72)on the above ansatz,it leads to the following terms at order

Requiring this to be zero,we can fix bpto be

The coefficient dpis fixed by the global normalization and we have

Therefore we fix the recursion relations to be

Fixing α = 1,we see that this is exactly the same recursion relation for thedeformed CFT.Then we can run the story in the reverse order.Namely,from the recursion relation we can write down the flow equation.Having the flow equation and assuming torus partition sum takes the form of sum over Boltzman weights (4.47),we can recover the Burgers’equation for the deformed spectrum.This shows that the result is exactly thedeformed CFT.

4.3.Non-perturbative features

In the previous sections,we have shown that thedeformed CFT is modular invariant and that by requiring modular invariance,one can fix the solvable deformation to be that of thedeformed CFT.In this section,we will explore some interesting non-perturbative features of the deformed partition sum.

4.3.1.Different signs and non-perturbative ambiguity.We have seen in section 3 that the deformed spectrum for the two signs of the coupling constant t (or equivalently in terms of the dimensionless coupling constant λ) have different properties.For the good sign,the spectrum is well-defined for arbitrary high energy states.On the other hand,for the ‘bad’sign,the deformed spectrum become complex for high energy states in the original theory and signifies a possible break down of unitarity.We will see that similar phenomena appears at the level of partition function.The solutions of the flow equation are different for the two signs of the coupling constant.For the good sign (corresponds toλ＞0 in our convention),the solution seems to be unique.For the bad sign,there are non-perturbative ambiguities.Let us first recall the recursion relation

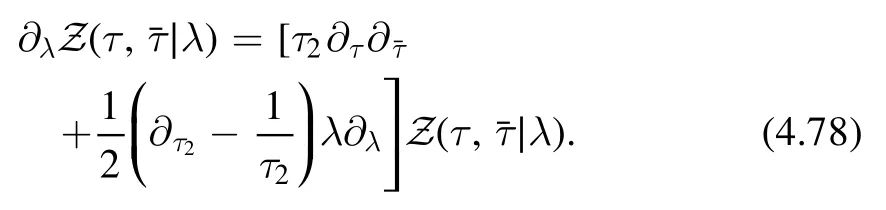
We want to study the solution of this equation with the initial condition

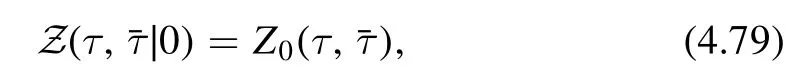
whereZ0(τ,) is the partition function of a CFT.We have seen that perturbatively we can constructZ (τ,) by the recursion relation (4.77).However,the flow equation also allows non-perturbative solutions in λ.

A non-perturbative solution.The simplest possible non-perturbative solution we can find is

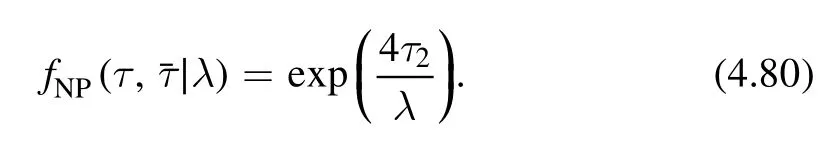
This solution is modular invariant and is indeed a solution of the flow equation.One interesting observation,that is also generalizable to thecase is that the exponent can be obtained from the Burgers’ equation.In fact the Burgers’equation allows two solutions if we do not impose the initial condition limλ→0En(λ) =Enwhich correspond to the two branches of the square root.Let us denote them by

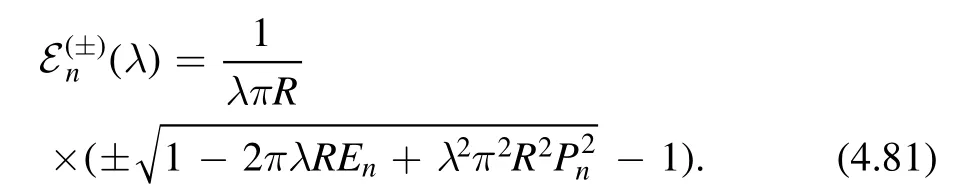
The solution which allows a well-defined CFT limit isTaking the sum of the two solutions,we obtain

We find that

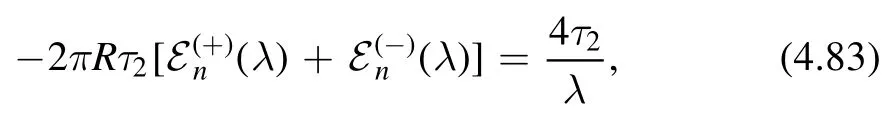
which is the exponent of the non-perturbative solution.We can consider more general solutions of this type by making the ansatz

Plugging this ansatz into the flow equation,we find thatX(τ,∣λ) satisfies exactly the same flow equation,but withλ→-λ.Namely,

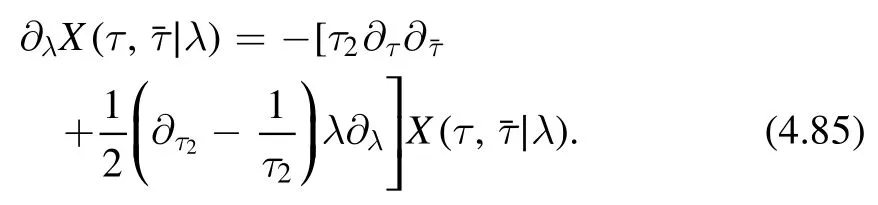
Different signs.Now let us consider the solution of the following kind

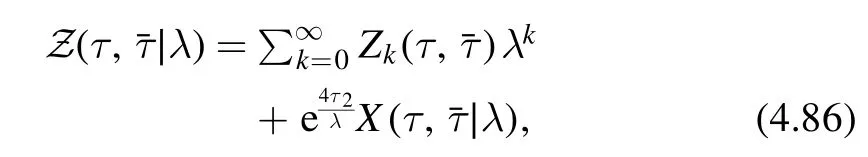
where the first term is our solution from the recursion relation(4.77).Now we consider the second term for two different signs.

For the caseλ＞0,the second term in(4.86)is divergent in the limitλ→+0 .Therefore the second term is not allowed by the initial condition

For the caseλ＜0,the factor=0and is thus compatible with the initial condition.There is no restriction on the functionX(τ,∣λ)apart from the flow equation(4.85).Therefore we can choose any functionX(τ,∣λ) satisfying(4.85).This is the non-perturbative ambiguity.

This is another manifestation of the possible break down of unitarity,which is consistent with what we have seen in the spectrum.One interesting point is that similar phenomena can be seen in the string theory side[22].For the two signs of the coupling constant,the deformed geometry is different.For the bad sign,the geometry has certain pathologies,such as naked singularities and closed time-like trajectory.By considering also thedeformation,we believe that the ambiguity is related to closed time-like trajectory.

4.3.2.Asymptotic density of states and hagedorn singularity.

In this section,we derive the asymptotic density of states fordeformed CFTs.We will see the density of states interpolates between the Cardy behaviorρ(E) ～and the Hagedorn behaviorρ(E) ～ e-E.Our derivation is similar to the derivation of Cardy's formula in CFT.

To derive the asymptotic density of states,we apply the S-modular transformation

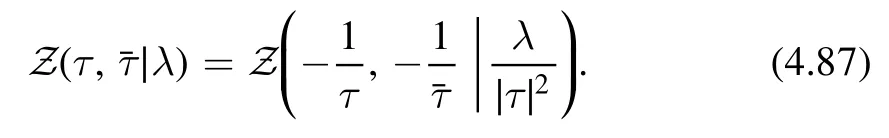
In addition,we choose the modular parameter τ to bewhich implies that

In this case,the partition sum simplifies to

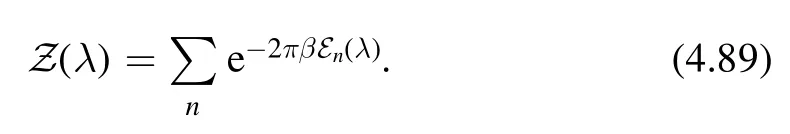
Now let us consider the low temperature limitβ→∞.In this limit,the partition sum is dominated by the ground state energy.The ground state energy of the deformed theory is given byandP0=0.From the expression of the deformed energy,we obtain

Notice that for this formula to make sense,we need to restrict ourselves to the regimeπ cλ＜6.We will make this assumption implicitly in what follows.The partition function in the low-temperature limit is thus given by

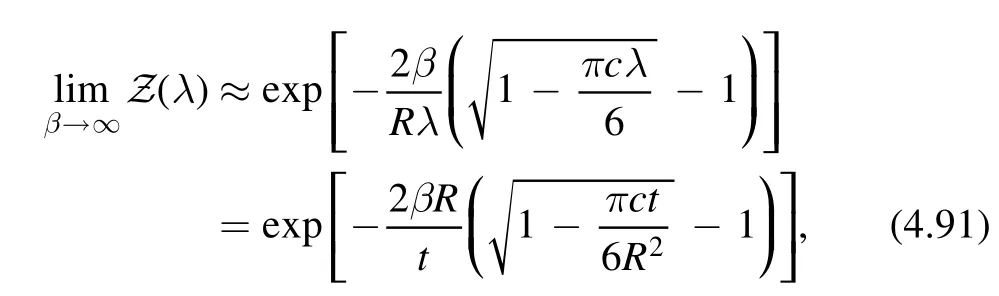
where in the second equality we have changed from the dimensionless parameter λ to the dimensionful parameter t.This makes the modular transformation slightly simpler since t does not change under modular transformation.Now we perform the S-modular transformation on (4.91),which is equivalent to exchange R and β.Physically,the S-modular transformation maps the low temperature limit to the high temperature limit.In the high energy limit,β≪1 and almost all the state contributes.We can thus define the following spectral density

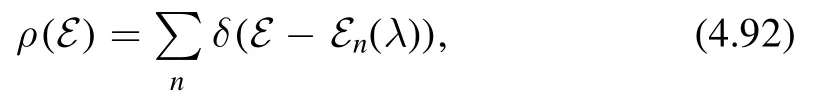
and write the partition function as

Identifying this expression with the S-modular transformation of (4.91),we obtain

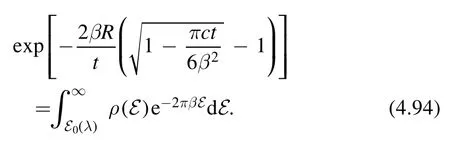
We see that the asymptotic densityρ(E) can be extracted by performing an inverse Laplace transformation

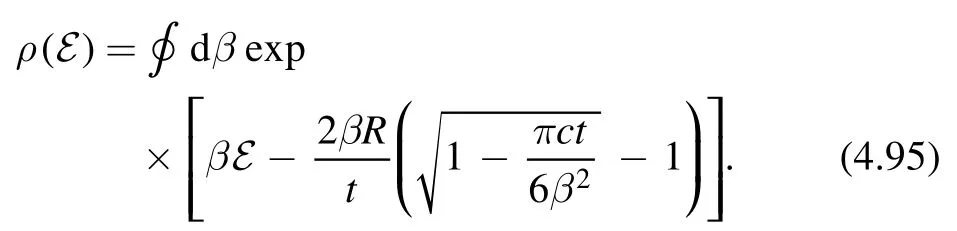
This integral can be computed by saddle-point,which is at

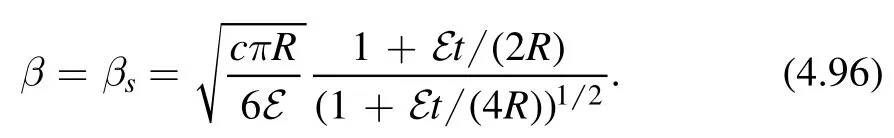
Taking into account the Gaussian fluctuations,we find

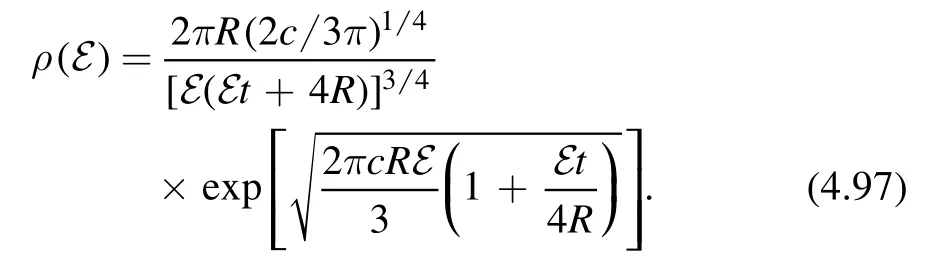
We can consider two limits,

· The IR limitEt≪R,we recover Cardy's formula for CFT

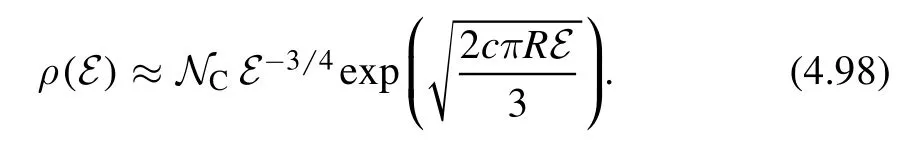
· The UV limitEt≫R,we find the Hagedorn behavior

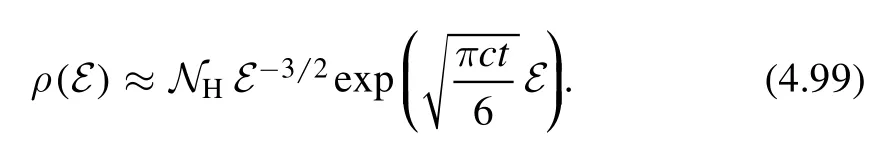
We can identify the Hagedorn temperature to be

The Hagedorn behavior in the UV implies that the partition function has a singularity nearβH.The scaling of the partition function near that point can be found by

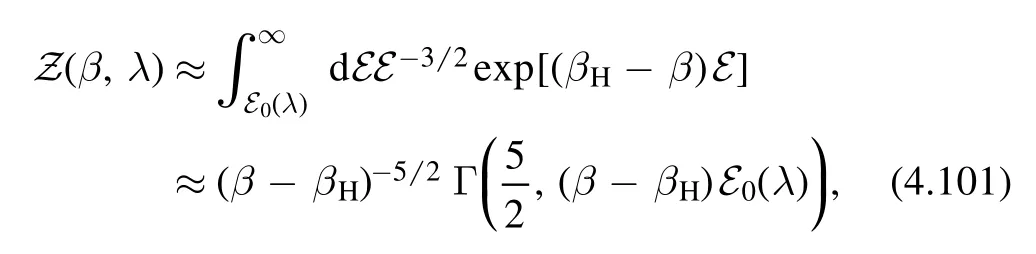
whereΓ(a,b)is the incomplete Gamma function.It is regular at b = 0.Therefore we see the nature of the singularity is a branch point.The Hagedorn growth of density of states is not the usual behavior of a local QFT,but rather the behavior of non-local theories such as the little string theory.

4.4.Uniqueness of deformation

As we mentioned in the previous section,for theories with an U(1) holomorphic current,one can define an irrelevant solvable deformation called thedeformation [3,36].This deformation is triggered by the irrelevantoperator defined by

whereand Θ are the components of stress energy tensor which appeared before in the definition ofbefore.J andare components of the U(1) currentJμ

For purely holomorphic current,we have=0.A factorization formula for thecan be proved in the same way as theoperator,which we discussed in detail in the previous sections.Putting the theory on an infinite cylinder,both the energy and the U(1) charge are deformed and the deformed quantities can be determined explicitly,similar to thecase.I n this section,we show that the deformed spectrum can also be determined from modular properties of the torus partition sum.The idea is similar to the discussion in the previous subsection for thedeformation,but it is technically more involved.

4.4.1.The set-up.Let us first give the set-up.For a CFT with U(1) current,we define the charged torus partition sum

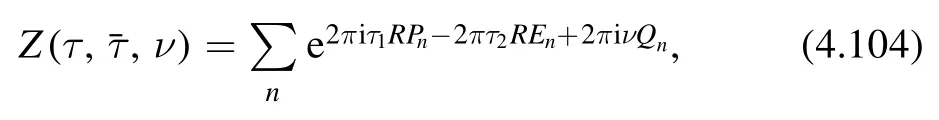
where ν is the chemical potential.We denote the common eigenstate of operatorsP,H,Qas ∣n〉 and

where for CFT we have

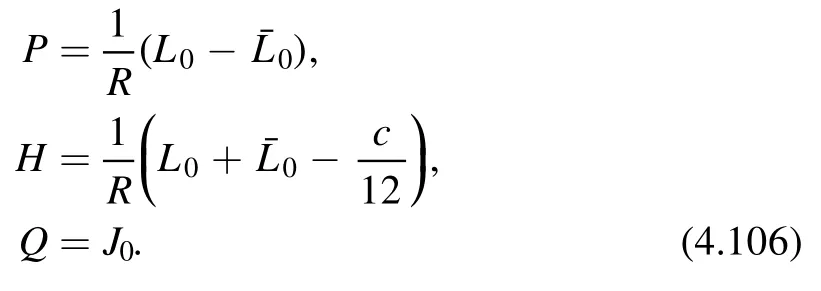
Here J0is the time component of the U(1) current.The charged partition function transforms as a Jacobi form of weight (0,0) and index k

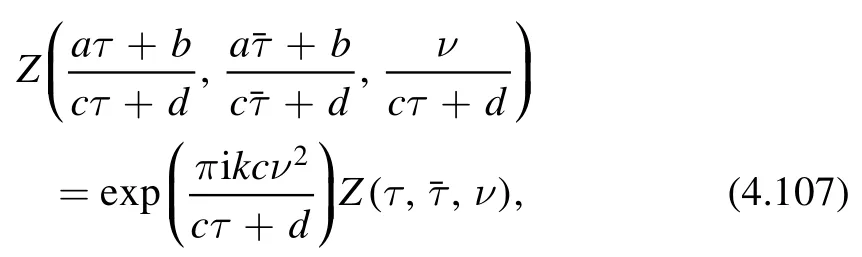
witha,b,c,d∈ℤandad-bc=1.Here k is the level of the U(1) affine Lie algebra

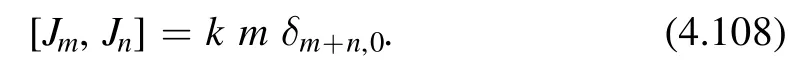
Note that (4.107) implies that the chemical potential ν transforms as a modular form of weight (-1,0).This is due to the fact that it couples to a holomorphic current of dimension (1,0) (see [37],section 3.1 for a discussion).

4.4.2.Deformations and perturbative expansion.Now we consider a solvable deformation of the following form

The deformed partition function is defined as

Similar to thedeformation,we require the deformed partition sum to be modular covariant

Plugging (4.112) into (4.111),we can perform the expansion of the deformed partition function

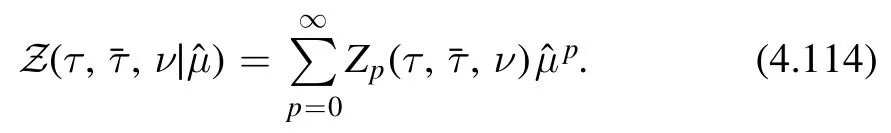
Modular covariance of the deformed partition sum,(4.113),implies that Zptransforms as a non-holomorphic Jacobi form of weight(0,p) and index k,

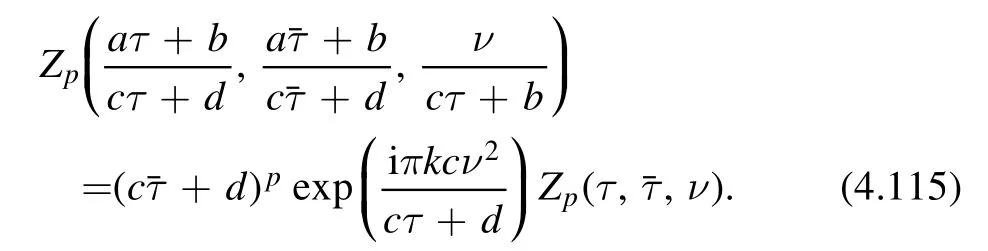
The first few orders in theexpansion are given by

where

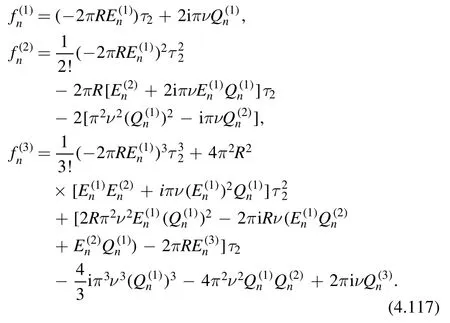
We can write Zpas a differential operator made ofacting on Z0.This is done by replacingin (4.117) by differential operators with the replacement rules

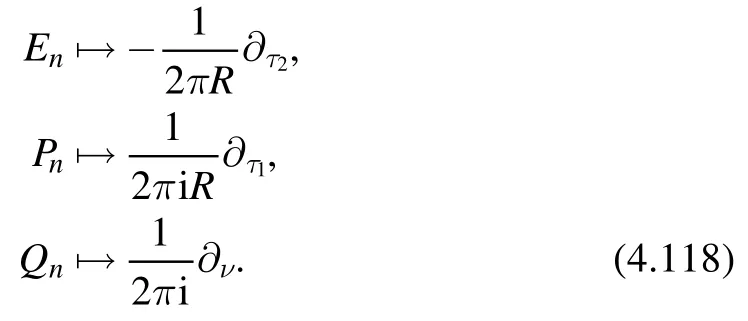
The above procedure leads to a double expansion of Zpin powers ofτ2and ν,

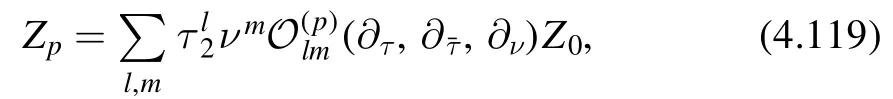
where the sum runs over the rangel,m= 0,1,…,p;0＜l+m≤p.As before,our strategy is to first prove uniqueness using induction and then give a way to construct the partition function which proves existence.

4.4.3.Uniqueness.It is clear that the differential operatorfor fixed p is only sensitive to the energy and charge shiftswithk= 1,2,…,p.Conversely,if we know allwith given p,we can determine all the energy and charge shifts withk≤pby using (4.116)-(4.119).

We can use the expansion (4.119) to prove that if Z1,…,Zphave been determined,Zp+1can be determined uniquely as well.As in the previous section,we start by considering the first step in this process.Equation (4.119) (with p = 1) takes the form

We are looking for differential operatorsfor which Z1transforms as a Jacobi form of weight (0,1) and index k,for any Z0of weight(0,0)and index k.To find them,we need a new covariant derivative with respect to the chemical potential ν in addition to the Maass-Shimura derivative.The new covariant derivative is given by

Acting withνD on a Jacobi form of weight(,) and index k gives a Jacobi form of weight (r+1,) and index k.The proof is basically the same as we did for the Maass-Shimura derivatives.

Using these covariant derivatives,it is straightforward to find a combination of the form (4.120) that has the correct modular transformation properties,

Here α is a constant that can be absorbed in the definition ofWe will set it to one below.It is not hard to check that(4.122) is the unique object of the form (4.120) with the correct modular transformation properties.

We are now ready to move on to the general induction step.We assume that Z1,…,Zp(with p ≥ 1) have been determined,and want to show that Zp+1can be determined as well.

We saw before that from the form of Z1,…,Zpwe can read off the energy and charge shiftswithk=1,2,…,p.Consider now the expansion (4.119) of Zp+1.Most of the terms in that expansion involve the energy and charge shifts withk≤p,which are assumed to be already known.There are only two terms in the sum,corresponding to(l,m) =(1 ,0) and (0,1),that involve the unknowns

To show that there is no more than one solution for the expansion (4.119),suppose there were two different ones.Subtracting them,and using the fact that most terms in the expansion (4.119) cancel between the two,we find that there must exist differential operatorssuch that

is a Jacobi form of weight(0 ,p+1)and index k,for any Z0which is a Jacobi form of weight (0,0) and index k.The fact that such differential operators do not exist(forp＞0)can be proven by using the properties of the covariant derivatives in a similar way to the proof for thecase.Since we have discussed this point in detail in the previous section we will not repeat it here.

4.4.4.Existence.We have shown that if a modular covariant deformation of the type(4.109)exist,then it must be unique.Now we want to give a way to construct the deformed partition function and find the deformed spectrum.The idea is again very similar to thecase.We first use the covariant ansatz approach to compute the first few orders and then give a recursion relation between different orders inexpansion.From the recursion relation,we can derive a flow equation for the partition function.From the latter,we can write down the flow equation for the deformed charges similar to the Burgers’ equation.Finally we solve the equations to find the deformed spectrum and find a perfect match with the results obtained from other approaches.

Covariant ansatz.In order to find Zp,we write down an ansatz with the desired modular properties,(4.115),and require it to be consistent with the general structure of the perturbative expansion,(4.119).The leading term inτ2is fixed by (4.119),(4.122),to be

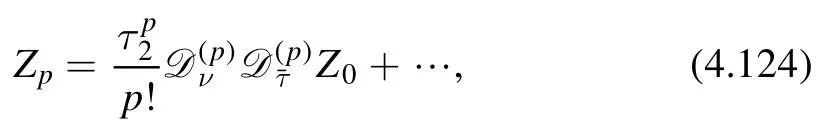
where

The other terms have lower powers ofτ2and can be written in terms ofwith 0 ≤i,j≤p.A term of the formwith particulari,ji s multiplied bysuch that its contribution to Zptransfor ms as a Jacobi form of weight(0,p) and index k,(4.115).Si ncehas weight

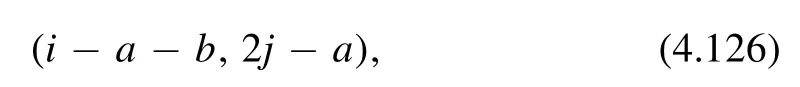
we have the constraint

The indicesi,jsatisfy the constraits 0 ≤i,j≤pand 0 ≤b≤p.This leads to

In addition,there are no terms witha=b= 0.Taking into account these constraints,we can write down the ansatz for any p.The first few Zptake the form

To fix the constantsa k,bk,ckwe impose the conditions which stem from the structure of the perturbative expansion.To be more explicit,we first expand the covariant derivativesandin terms of∂νandin the ansatz.Comparing with the structure of the perturbative expansion,we impose the following conditions

· The coefficients of the terms withoutτ2and ν,namelyare zero.

· The coefficients of terms with negative powers ofτ2,i.e.

We find that these conditions are powerful enough to fix Zpcompletely at any given order.The solutions for the first few orders are given by

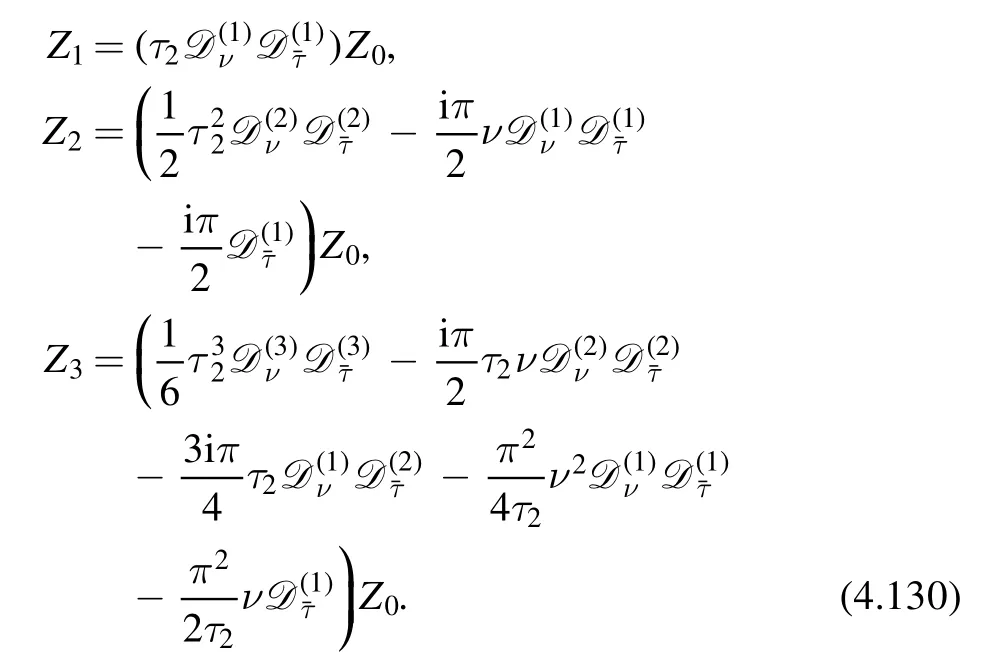
This approach enables us to find explicitly Zpto any order in principle.

Recursion relation.In practice,it is more convenient to write down a recursion relation.It turns out that such a relation exists,but it is more complicated than thecase.In particular,it relates Zpto all Zjwith 0 ≤j＜p.It takes the form

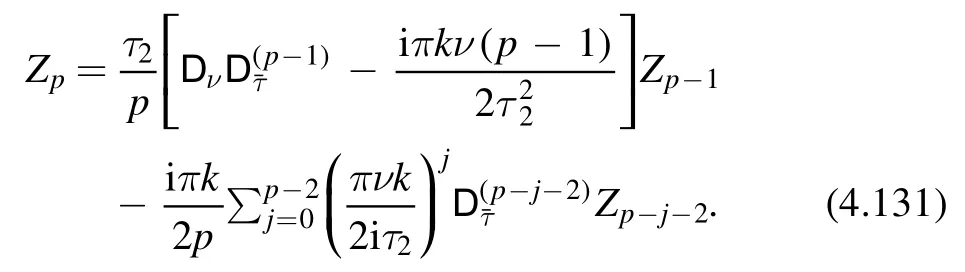
We see that Zpdepends on all of the lower order quantitiesZ1,…,Z p-1while in thecase,Zponly depends onZp-1.Nevertheless,the recursion relation (4.131) can also be phrased as a differential equation for the partition sum.Namely,if the partition sumsatisfies

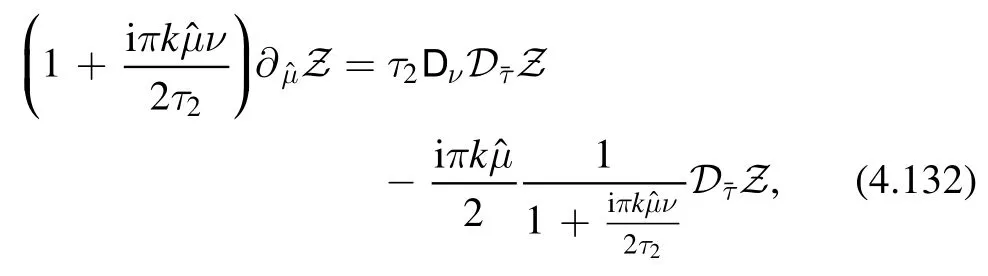
where

then expanding this equation in a power series inreproduces (4.131).For thecase,the flow equation for the torus partition sum can also be derived from a description with a dynamical metric [13,104].It would be interesting to derive (4.132) from a similar point of view,by including a dynamical gauge field as well.

Deformed spectrum.From the equation (4.132) we can read off a system of differential equations that describes the evolution of the energies and charges of states with the coupling.To do that,we plug the the partition sum(4.111)into (4.132),and compare the coefficients of a given exponential on the left and right hand sides.We also multiply by the factoron both sides.The resulting equation then takes the form

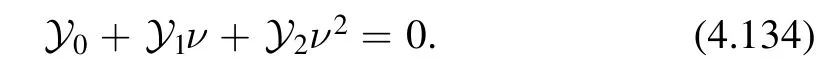
Here,Yiare functions containingand the derivativesSince this should hold for all values of ν,we haveY0,1,2=0.The equations Y1- Y2=0and Y2=0respectively yield

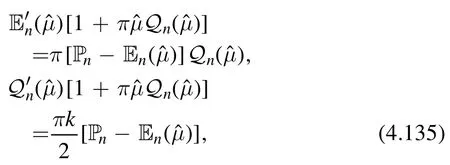
Dividing the two equations in (4.135),one finds that

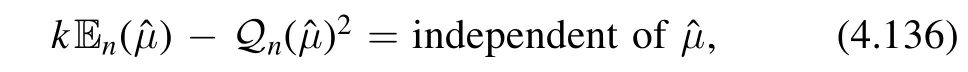
which reproduces one of the results of [36].

Equations (4.135) can be expressed in a form that is closer to Burgers’ equation by writing them in terms of the dimensionful couplingμ=,and using the fact that the dimensionless energiesEndepend only on the dimensionless coupling.

The resulting system of equations can be written as7To reproduce the equations given in [36],we need to make the replacement

The differential equation on the second line of (4.137) looks like the inviscid Burgers’ equation with a time-dependent source,where the coupling μ plays the role of time.The dynamics of this source is described by the first line of (4.137).

The solution of (4.137) with the boundary conditions En(0) =EnandQn(0) =Qnis given by

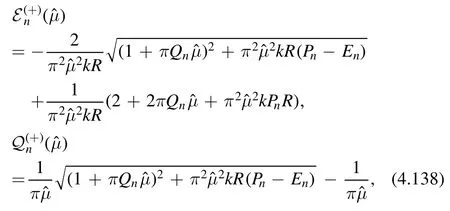
where we took the positive branch of the square root,so that

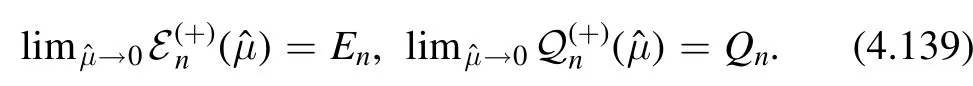
This spectrum indeed matches with the one of thedeformed CFT.

Let us notice that thedeformed spectrum does not depend on the sign of the deformation parameter.This is different from the case of thedeformed spectrum.The spectrum for both signs ofbehaves like the bad sign of thedeformed spectrum.Namely,the spectrum become complex for high enough energies of the original theory.

4.4.5.Non-perturbative aspects.Now we consider some non-perturbative features of the partition function using the flow equation (4.132).As one might expect,since thedeformed spectrum behaves like the bad sign of thedeformation,there are non-perturbative ambiguities in the solution of the flow equation.

A simple way to investigate them is to consider the contribution to the partition sum of states for which we take the negative branch of the square root in (4.138).The two branches are related by

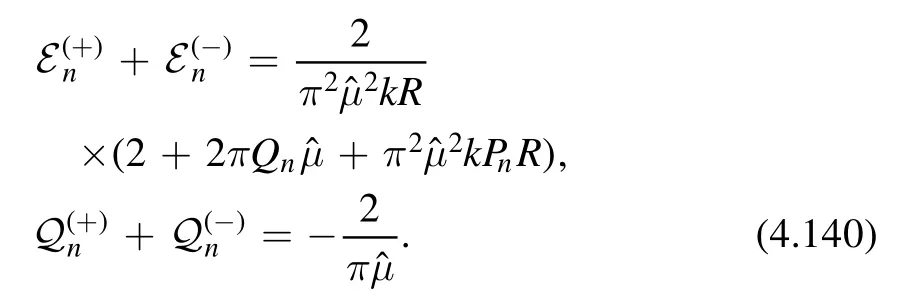
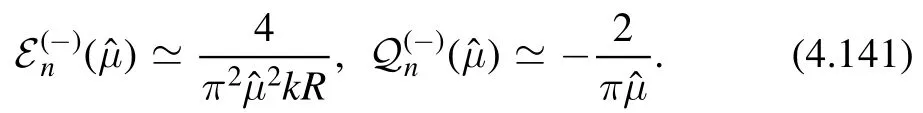
One way to find consistent non-perturbative contributions is then to assume that we have some extra states in our theory labeled byn~,whose energies and charges are given byandThese states can be the negative branch energies and charges of some otherdeformed CFT,that a priori need not have anything to do with the one that gives the perturbative contributions discussed above.We find

Using the relation

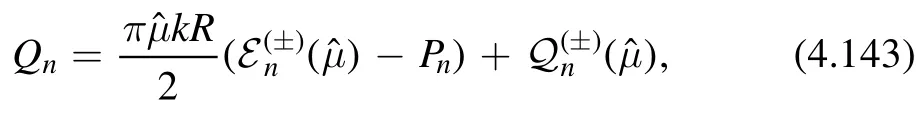
satisfied by both branches of (4.138),we can rewrite (4.142)as

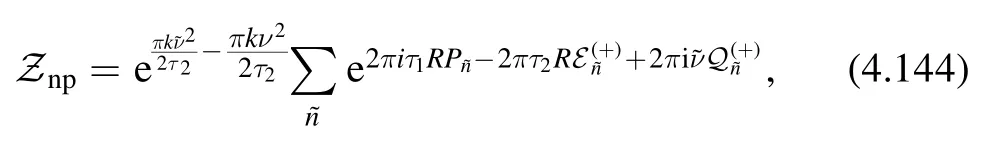
where the shifted chemical potential is given by

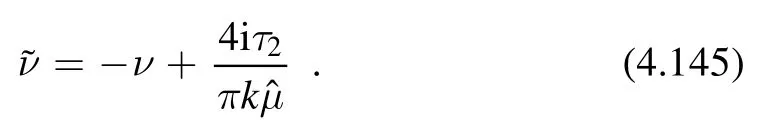
By construction,the partition sum (4.144) must be modular invariant (since the original expression (4.142) is).This can be shown directly as follows.The prefactors in (4.144)transform as

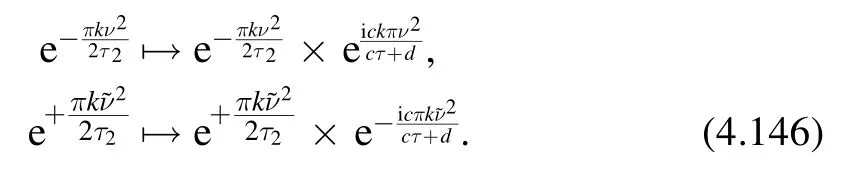
The partition sum on the right-hand side of(4.144)transforms as

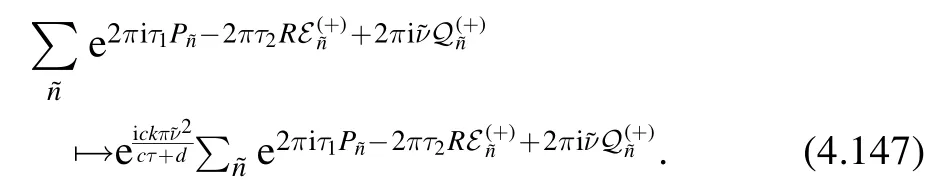
Combining these transformations,we see that Znp(4.144)indeed transforms as a Jacobi form,(4.113).

The fact that Znpis a non-perturbative contribution to the partition sum is due to the behavior as→0of the prefactor on the right-hand side of(4.144).The leading behavior of the partition sum in this limit iswhich is exponentially small for both signs of,as expected.Thus,we see that the non-perturbative completion of the partition sum ofdeformed CFT has a similar ambiguity to that for adeformed CFT.

5.Gravity and holography

In this section,we present several different perspectives ofdeformation.In particular,its relations to 2D gravity theories and holography.We first present Cardy's random geometry point of view,this provides us an alternative explanation for the solvability ofdeformation.We also derive the flow equation for the torus partition function from this perspective.We then discuss a path integral formulation ofdeformation,which is related to the 2D topological gravity.We will derive the deformed S-matrix and partition function from this definition.Finally we consider the holographic dual of thedeformed CFT.The proposal is quite simple and has passed several non-trivial checks.Since in this section we consider several different topics,we will only present the main results and key steps of the derivations.For more details,we refer to the original papers.

5.1.Random geometry

Thedeformation can be interpreted as coupling the original QFT to a random geometry [13].Using this interpretation,one can derive a flow equation (or evolution equation if we view the coupling t as time) for the torus partition function.At the same time,it provides an alternative point of view on the solvability ofdeformation.

The analysis can be performed in two steps.In the first step,using the fact that theoperator is quadratic in components of the stress energy tensor,one performs a Hubbard-Stratonovich(HS)transformation of the variation of the partition function.The HS transformation introduces auxiliary variables hijwhich couple to Tijand have the natural interpretation as the fluctuation of the metric,or infinitesimal fluctuation of the spacetime geometry.The auxiliary ‘gravity sector’ can be solved by saddle-point approximation and the on-shell action turns out to be a total derivative.This is the reason for the solvability of thedeformation.In the second step,if the variations of spacetime geometry is uniform,one can rewrite the fluctuation of the metric hijin terms of the variation of parameters that specify the geometry.This leads to a diffusion type equation which can be used to study the deformation of the partition function.In what follows,we mainly discuss the deformed partition function on a torus.For other interesting geometries,we refer to the original paper [13].

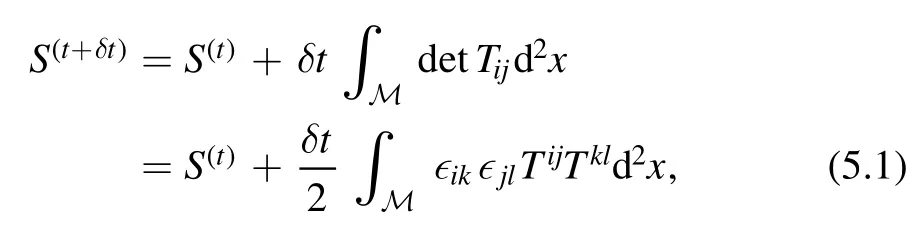
where M is the domain on which we define the theory.We work in the Cartesian coordinate system and use the relation

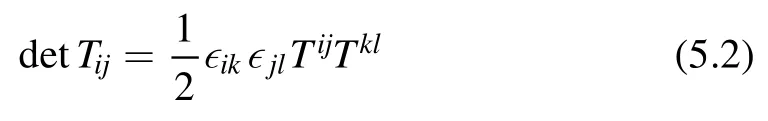
in the second equality.Since detT ijis quadratic in components of the stress energy tensor,we can rewrite the infinitesimal deformation of the partition function by performing a HS transformation,which is nothing but a fancy name for Gaussian integral

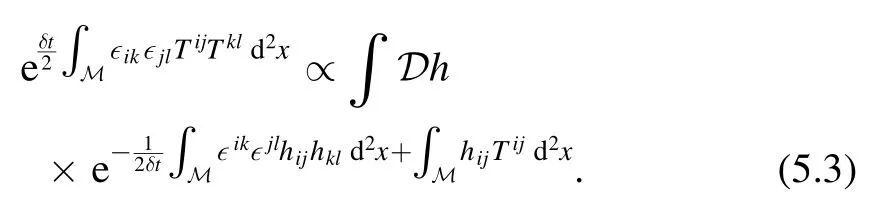
By the definition of stress energy tensor Tij,the second term is equivalent to an infinitesimal change in the metricgij=δij+hij.Several comments are in order.

1.We notice that the ‘gravity action’

is not the linearized Einstein-Hilbert action,so it is not really a standard gravity theory.

2.The infinitesimal parameterδtappears in the action(5.4) asSinceδt→0,the gravity sector is dominated by the saddle-point.So we can restrict our considerations to the saddle-point.

3.In principle the functional integral should be performed over all possible hij,including the ones with non-zero curvature.However,as we will show,it is enough to restrict ourselves to the flat metrics.

Restriction to flat metrics.In two dimensions,any infinitesimal deformation of the metric can be written as

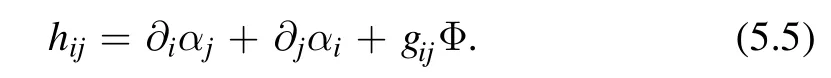
This is because any 2D metric is locally conformal flat.The first two terms in (5.5) correspond to an infinitesimal diffeomorphismof the Euclidean metric.The last term in (5.5) corresponds to an infinitesimal change of scale.We will show that we can take Φ = 0.The derivation is based on the saddle-point equation and the conservation of stress energy tensor.Due to the saddle-point equation,

Or equivalently,

Notice that in the above equations hijare at the saddle point.The conservation of stress energy tensor∂i Tij=0can be translated to an equation about the metric

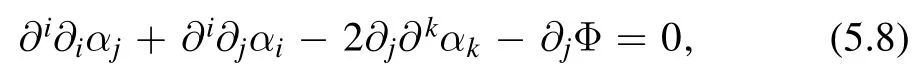
where repeated indices are summed over.This is equivalent to

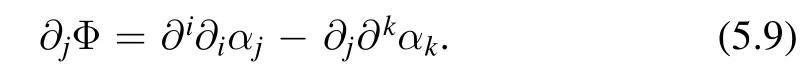
It is then easy to see that

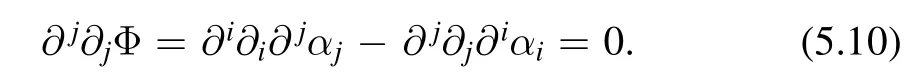
This implies that Φ can be absorbed into a redefinition ofαi.It is easier to see this in the complex coordinate(z,.The equation (5.8) can be written as

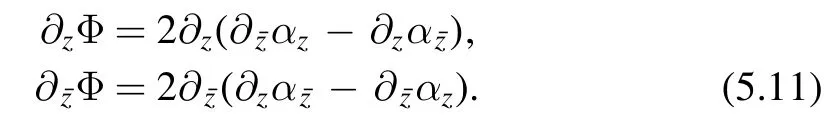
Since we know from (5.10) thatwe can write

for some functionsf(z)andCombining with(5.11),we find

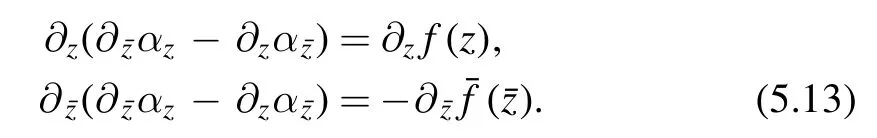
So we can take

If we define

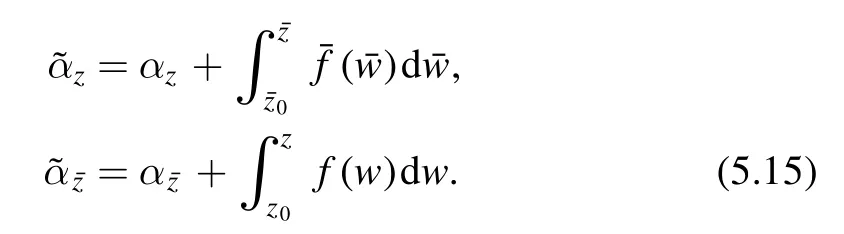
Then we have

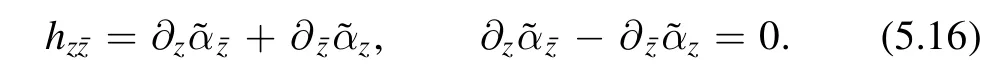
To conclude the discussions so far,to define the path integral in (5.3),we can restrict to the following class of metrics

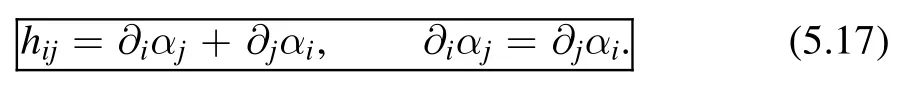
Using the second equation,we can writehij= 2∂i αj.Therefore we can write the gravity action as

which is a total derivative.We can thus write down the full action as

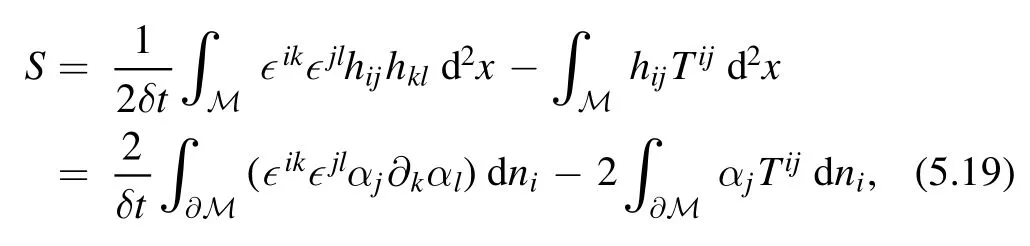
where ∂M is the boundary of the region and niis the outward pointing normal vector.Alternatively,the boundary action can also be written as

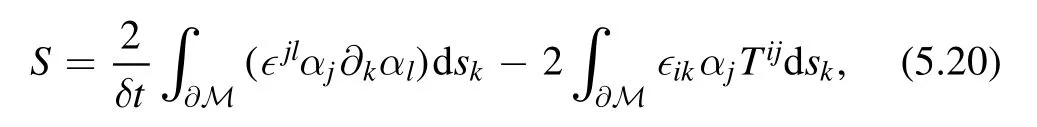
where skis now the tangent vector.We can perform the path integral over the new variablesαisince it is a rewriting of hij.However,we should not forget the constraint (5.17)∂iαj= ∂j αi.This can be rewritten as

From the discussion so far,we find that after rewriting in terms of hij,the gravity sector is in a sense topological and reduces to a boundary action.Topological theories are typically solvable,and this is the main reason of the solvability of thedeformation.This already gives us an alternative explanation for the simplicity ofdeformation.In addition,it gives us a way to write down a flow equation for the deformed partition function.

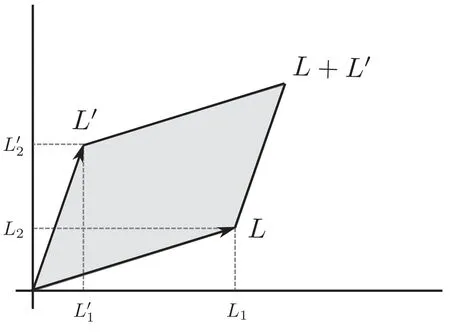
Figure 2.The parallelogram which is identified with the torus.

5.1.2.Flow equation for partition function.For definiteness,we consider the torus partition function.Following Cardy[13],we take the four end points of the parallelogram to be 0,L,L′,L+L′withL=L1+iL2andas is shown in figure 2.Firstly we want to argue that although we are performing a functional integral over the fluctuations of the metrich ij(x) in (5.3),in fact only constant flat metric hijcontributes.This is actually very natural.The random geometry is basically a rewriting of the effect ofdeformation on partition function at the linear order,namely.In conformal perturbation theory,the effect is given byδtWe have seen that in factis a constant due to translational invariance.If we relate this deformation to the fluctuation of the spacetime geometry,the effect should be the same everywhere.In other words,this is a uniform deformation.This implies that hijshould be position independent and the functional integral actually reduces to the usual integral.We can therefore write

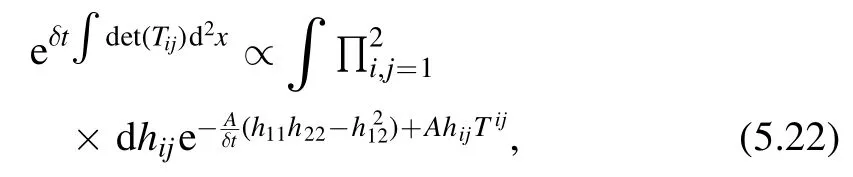
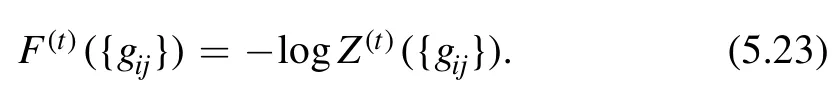
We can write the second term in the exponent as

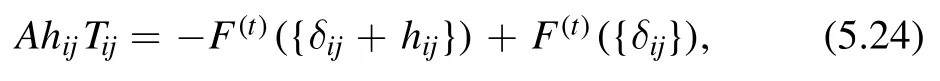
and we have the following equation for the deformed free energy

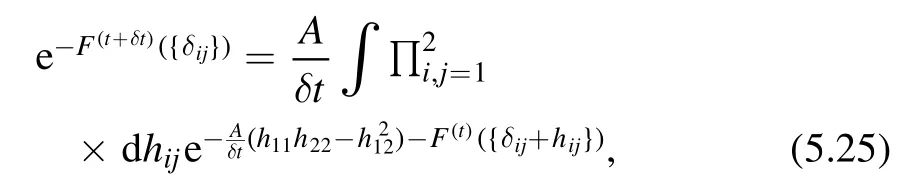
where we have put in some factors to the measure which are not essential.

A small lemma.To proceed,we need a small lemma by Cardy.The proof is given in the original paper.The statement is as follow.Suppose we have an integral over N variables{Xi}.If the quantityZ(t)({X})satisfies the relation

Then the quantityZ(t)({X})obeys the following equation

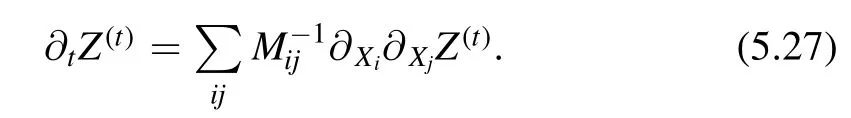
In terms of the quantityF(t)= -logZ(t),the differential equation is given by

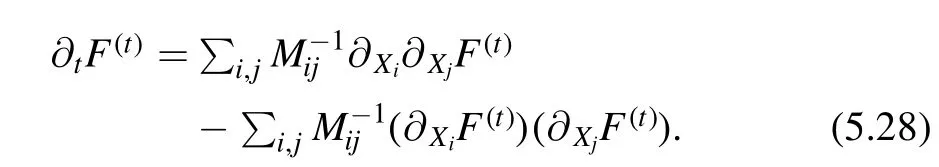
Variations in parameters.For a geometry without boundary such as a plane,thedeformation does not change the spectrum,or equivalently it does not have any effects on the deformed partition function.On the other hand,when we put the theory on the torus,the constant fluctuation will deformed the shape of the torus in a uniform but nontrivial way.This affects the partition function.The shape of the torus is specified by L andL′,which are shifted toL→L+δLandL′ →L′ +δL′.These shifts are related to the uniform variation of the metric by

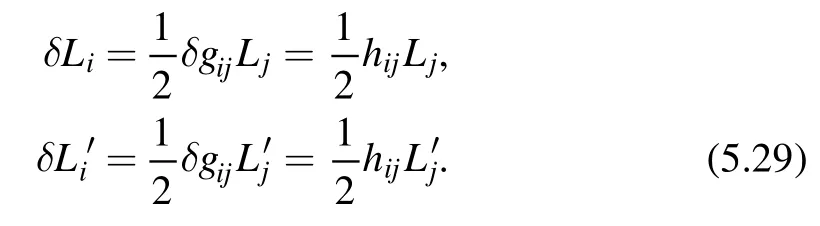
Using these relations,we can rewrite the fluctuation of the metric in terms of fluctuation of the parameters LiandFrom the lemma (5.26),we can write down the following differential equation for the partition function

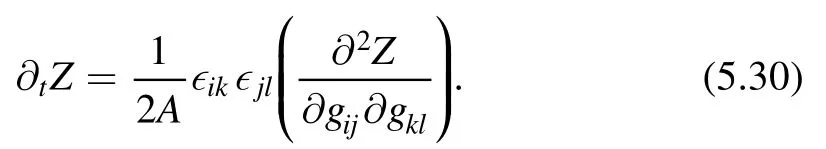
Or equivalently,in term of F

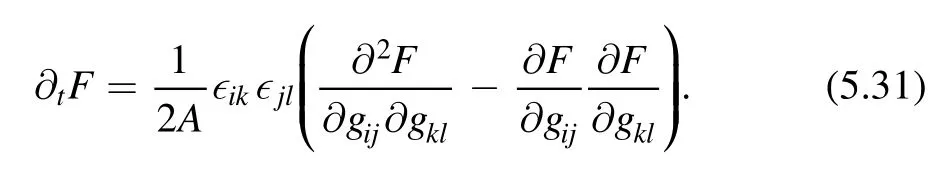
The derivative of F with respect to gijis given by the onepoint function of stress energy tensor

In the second equality,we have used (5.29) and

By translational invariance,(5.32) can be written as

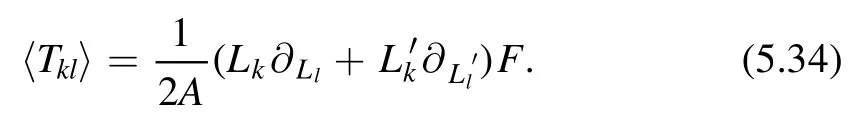
In general,for any local operatorO (0),

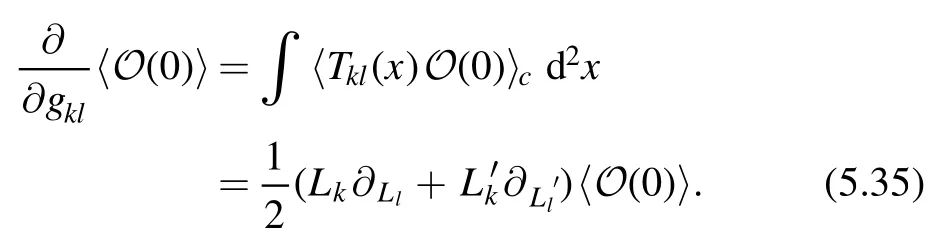
Therefore we have

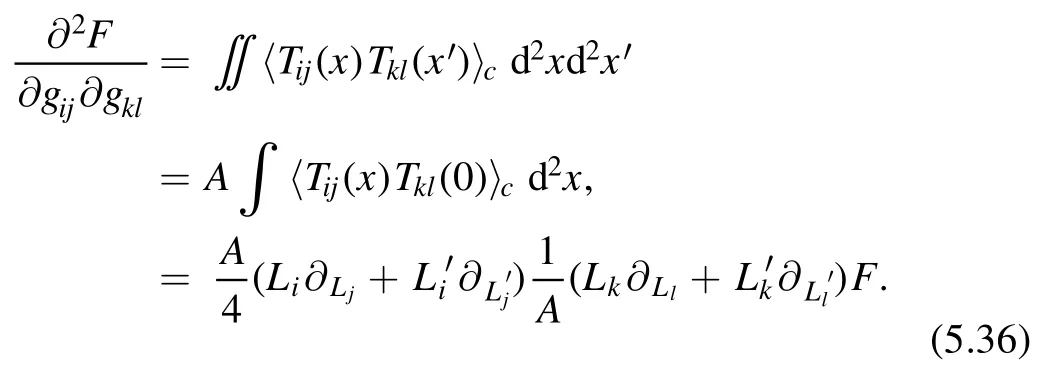
Then (5.31) can be written as

Equivalently for the partition function

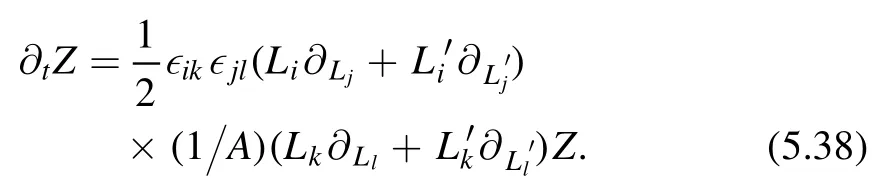
To write this equation in a nicer form,we can introduceThe equation for Z is given by

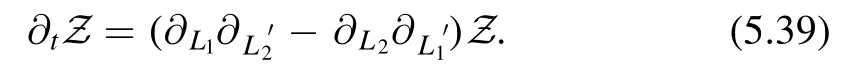
The flow equation (5.38) is equivalent to (4.38) that we derived in section 4 by the simple identification

5.2.2D topological gravity

The random geometry point of view rewrites the infinitesimal deformation of the partition function in terms of fluctuations of spacetime geometry.In this way,we can only derive the flow equation for the partition function.Can one somehow‘integrate’ the flow equation and give a path integral definition of thedeformation? Such a definition was proposed in [9,104].The proposal is thateforming a 2D QFT is equivalent to coupling the theory to a 2D topological gravity which is similar to flat spacetime JT gravity.In this section,we discuss this interesting proposal.Before going into the details,it is worth emphasising that the gravity theory which is proposed in [9,104] is not exactly the JT gravity.On the plane,the gravity theory is almost the JT gravity.This is enough for deriving the deformed S-matrix.For computing torus partition function,however,one has to resort to the first order formalism and strictly speaking the theory is no longer the JT gravity.

There are several checks for this proposal.Firstly,one can show that under thedeformation,the S-matrix is deformed in a simple way by multiplying a CDD factor.Secondly,by performing the path integral carefully,one can derive the flow equation which we derived in the previous section.The derivations are technical,so we will present the main ideas and some of the key steps for the derivation.More details are referred to the original papers and references therein.

5.2.1.The proposal.The proposal of [9,104] is as follows.Thedeformed action is given by coupling the theory to the flat spacetime JT gravity

whereS0(gμν,ψ) is the original field theory which minimally couples to the dynamic metricgμν,but it does not couple directly to the dilaton φ.The second term is the gravity sector.On the plane,this action can be written equivalently in the first order formalism which we will write down in (5.87) in the next section.The vacuum energy Λ is related to thecoupling constant t by

Unlike Cardy's random geometry interpretation,which is an alternative interpretation about the infinitesimal deformation of the partition function around a given point t.The definition(5.41)is a complete and non-perturbative definition of thedeformed theories along the whole flow.In this formulation,the relation betweendeformation and gravity is manifest.

The gravity sector is purely topological and does not have propagating degrees of freedom.The dilaton field plays the role of Lagrangian multiplier and forces the spacetime to be flat.Since the gravity sector is topological,the action again can be written as a total derivative and interesting physics happens at the boundary.

5.2.2.Gravitational dressing.In the previous sections,we have studied the deformed spectrum and partition function of thedeformed theories.We now turn to another observable which is the S-matrix.The S-matrix relates incoming and outgoing asymptotic states in a scattering process and is one of the most important physical observables in QFTs.An Smatrix element can be parameterized by the four-momenta and other quantum numbers of the scattering particles.For our purpose,we consider the S-matrix in 1+1 dimensions.The four-momentum is given bypμ=(E,p) where E is the energy and p is the momentum of the particle.We denote the collection of all four-momenta byTo simplify our notation,we omit other quantum numbers of the particles and write the S-matrix element asS({pi}).As we will show below,underdeformation,the S-matrix is deformed in the following simple way

Derivation of the deformed S-matrix.There are several ways to arrive at the deformed S-matrix.The simplest way is via a geometrical interpretation of thedeformation.From the random geometry point of view,we already see that turning ondeformation has the same effect as deforming the spacetime geometry.Therefore we can take two different point of views fordeformation.

1.The spacetime geometry is fixed,we perform an irrelevant deformation of the QFT on the fixed background.This is the original definition of thedeformation.

2.The spacetime is deformed in a dynamical way via a dynamical change of coordinates.The new coordinates depend on the stress energy tensor of the QFT.On the new coordinates,the theory ‘looks’ undeformed.

Of course,to make the second point of view more precise,we need to first specify the change of coordinate and then make clear the meaning of ‘looks undeformed’ in the new coordinate.As we will see,coupling the theory to 2D gravity provides a convenient way to find the dynamical coordinates.We will make the meaning ‘looks undeformed’ more precise when deriving the gravitationally dressed S-matrix.

We want to emphasis that the second point of view for thedeformation is potentially very powerful and its range of application is beyond the deformed S-matrix.At the classical level,this change of coordinate is constructed recently in [39] from a different consideration.A similar interpretation for thedeformation as dynamical change of coordinate (or field depend change of coordinates) is also proposed recently in [40,41].

For our purpose,it is convenient to work in the light-cone coordinate

The vacuum solution of the JT gravity is given by

whereα,β= ±,c is some constant.We haveη+-=η-+= -1 andη--=η++=0.We want to study scattering around this vacuum.We see that although the metric is invariant under Poincaré groupx±↦x±+a±,the vacuum solution of the dilaton is not.This implies that the deformed vacuum is not invariant under the Poincaré transformation in the original coordinate systemx±.The vacuum solution of the dilaton is invariant under the combined transformation

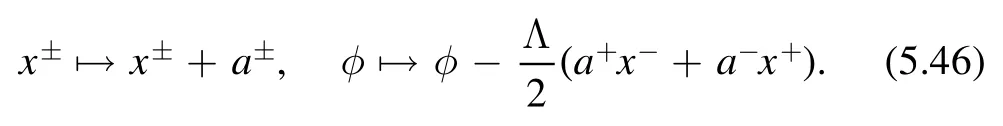
If there exist a new coordinate systemX±(x+,x-) on which the theory looks like undeformed,then it must has the Poincaré invarianceX±→X±+a±and it should involve φ in some way.This is a requirement for the new coordinates.To proceed,we work in the conformal gauge

Then the gravity action becomes

The equations of motion for φ and Ω are given by

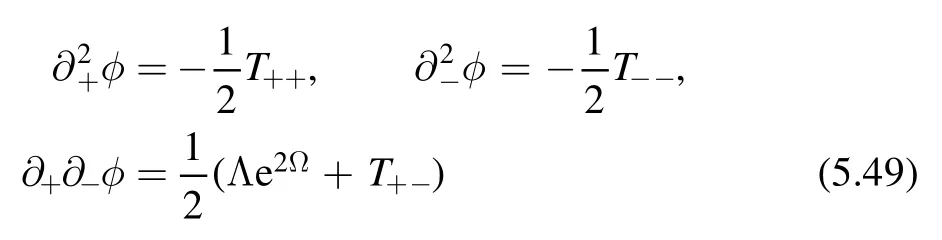
and

The general solution for Ω is thatfor two arbitrary functionWe impose the boundary condition thatgαβ→ηαβat infniity.This implies that Ω = 0 everywhere.So (5.49) simplifies to

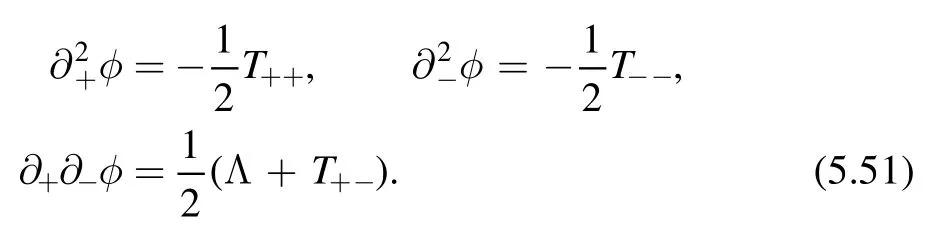
The main proposal of [9] is that we should take dynamical coordinateX±(x+,x-) to be

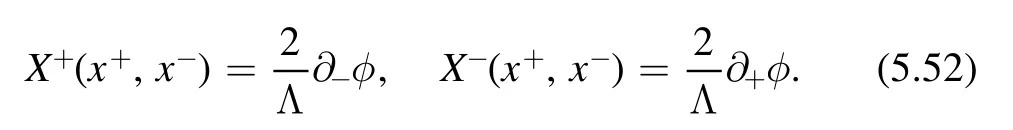
Let us separate the original coordinates and write

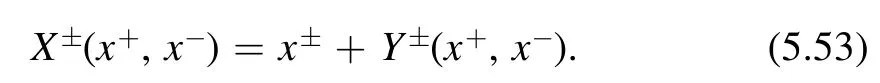
Then the equations of motion for the dilaton imply

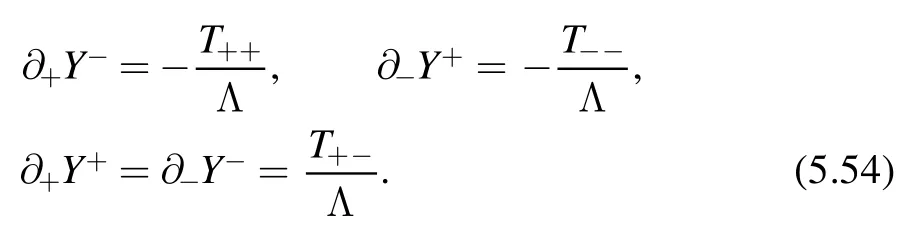
This is equivalent to the following change of coordinates

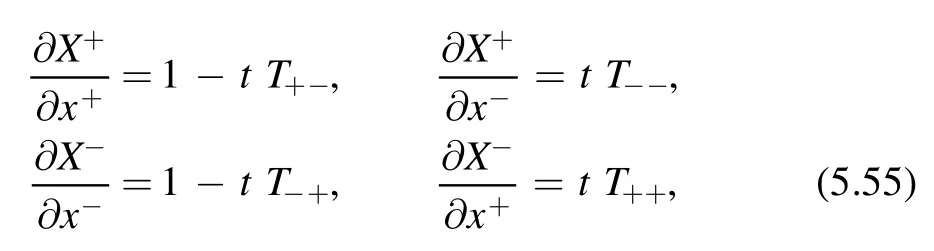
which coincides with the proposal in [39].We see that the transformationX±+const,which is equivalent to the combined transformation (5.46) indeed leaves the vacuum invariant.

Despite this nice feature,we see that the change of coordinates(5.55)is rather unusual.Normally if we specify a change of coordinate,we writeX±=f±(x+,x-) with some given function.Here,however,we specify the change of coordinates in a differential formwithbeing an operator that depends on the stress energy tensor.Strictly speaking,this ‘change of coordinates’ is an operator equation.This makes is a bit subtle to interpret at the quantum level.At classical level,we can treatas usual functions.The differential form of (5.55) is related to nonlocality ofdeformation.In order to find the dynamical coordinateXαexplicitly from (5.55),we need to perform integrals,which is a non-local operation.

Now we consider the scattering problem in 1+1 dimensions and see how we can make (5.55) more precise in this simple context.This can be done in two steps.Firstly we work out the dynamical coordinates explicitly using some special features of scattering in 1+1 dimensions;Then we use the dynamical coordinate to perform the mode expansion of the free field,which leads to the dressing of the asymptotic states.

Dynamical coordinate.Let us denote the set of on-shell momenta of the incoming and outgoing particles as{pi} and{qi} respectively.Then the stress energy tensor is that of a collection of particles.We can find the quantities±Yby integrating (5.54).For example,

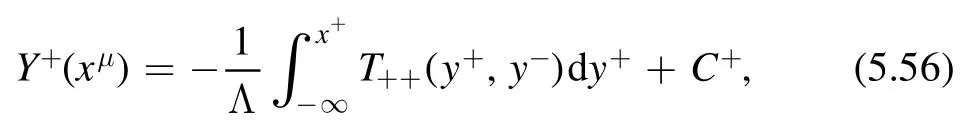
whereC+is an integration constant.We have similar expression forY-(xμ).In order to fixC+,we need to impose boundary conditions.In what follows,we denote the spacetime coordinate byxμ=(t,x).The total momentum of the light-cone components are given by

Figure 3.The ordering of particles.The ordering of the rapitities are the same as the orderings of the spacetime positions.

We can impose the condition that at infinite left,the coordinatesY±are given by

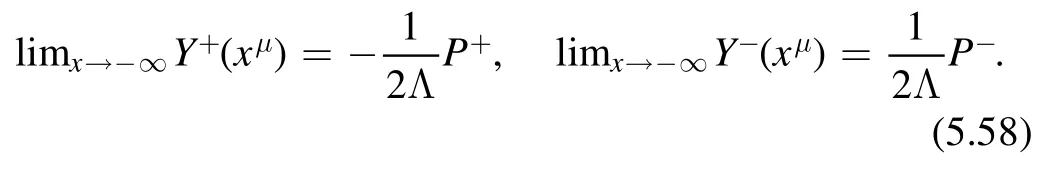
These conditions fix the constants±Ccompletely.From this,we can deduce that at infinite right,we have

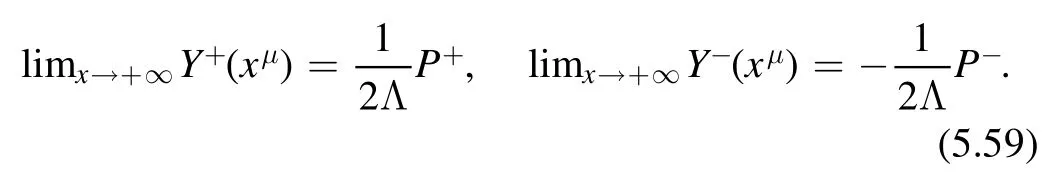
We focus on the incoming particles first.In 1+1 dimensions,we can parameterize the momenta of the particle by rapidities.Let us denote the rapidities byθ1,…,θ N.One special feature of scatterings in 1+1 dimension is that the rapidities are ordered.We can take the following ordering

where the positive rapidity corresponds moving towards right and the negative rapidity correspond to moving towards left.For incoming particles,this ordering is equivalent to the ordering of particles in space.The reason is simple.In 1+1 dimensions,all the particles are placed along a line.In order for the scattering to take place,for the incoming particles,the leftmost particle (moving towards right) must move faster than the other right moving particles,otherwise it cannot catch up with them and will miss the scattering.This is shown in figure 3.

The positions of the particles are denoted byx1,…,x N,we have

In the far past where t→ -∞,the particles are well separated,we have

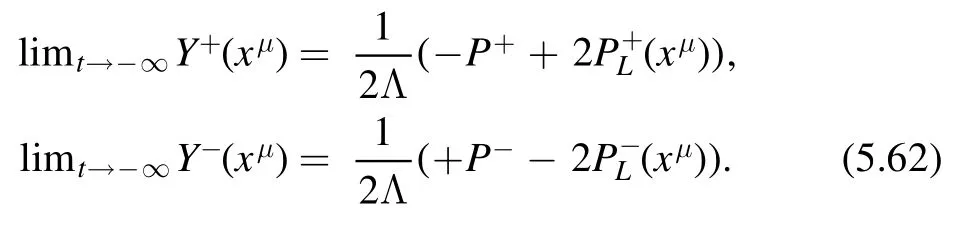
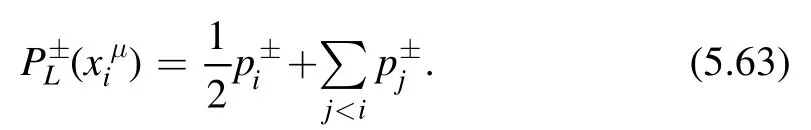
Plugging the prescription (5.63) in (5.62) and recalling that

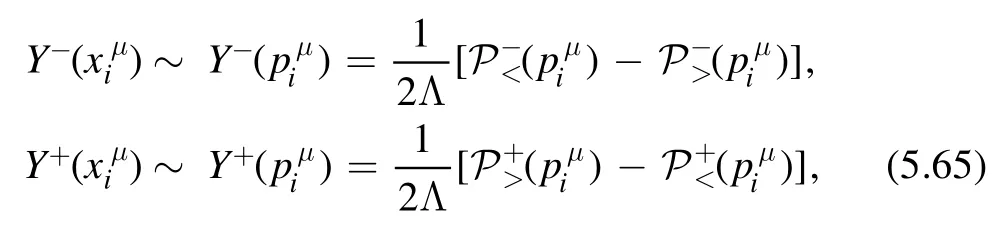
Dressing asymptotic states.To compute the S-matrix,one needs to prepare asymptotic states in the far past.In this asymptotic regime,before introducing gravity,the matter field can be decomposed as

As we discussed before,after introducing gravity,the effect can be encoded in a dynamical change of coordinates.Therefore if we use the new coordinatesXμ,the theory should‘look the same’in the asymptotic regime.More precisely,all we need to do is to perform the same decomposition,but using new coordinate systemXμ.Accordingly,we need to define a set of new creation and annihilation operatorsAin(p)andsuch that

The precise meaning of ‘looks undeformed’ in our context is to identify the ψ in (5.66) and (5.67).We then find

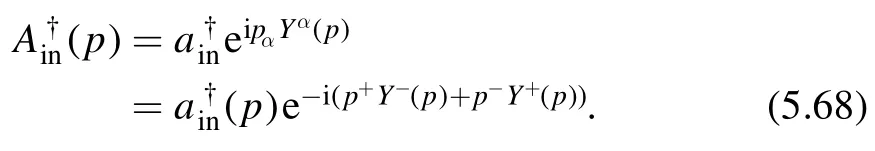
The dressed incoming asymptotic state is generated by the action ofas

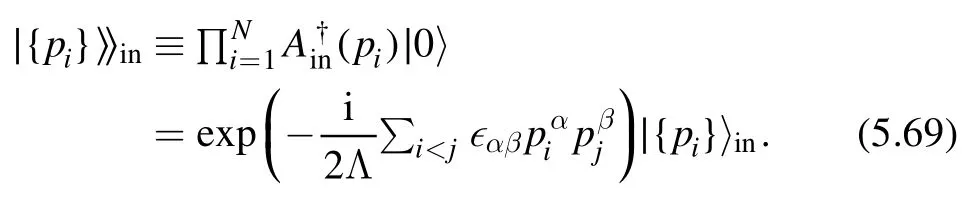
A similar analysis can be done for the outgoing states.The only difference is that the ordering is reversed which leads to a sign flip

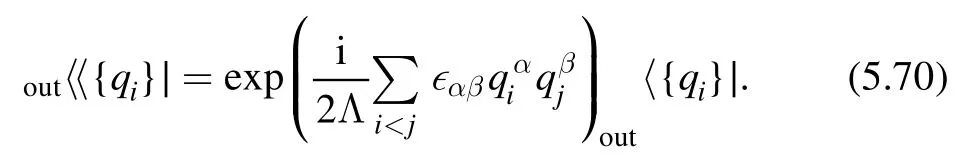
From the definition of S-matrix,

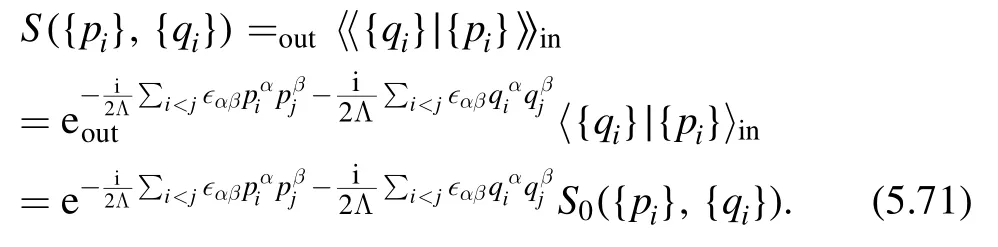
This is the gravitational dressing formula for the S-matrix in (5.43).

CDD factor and S-matrix.The dressing factor in(5.43)is a CDD factor.Here we discuss in more detail about these factors and their physical effects.The CDD factor(sometimes called CDD ambiguity),which is a short name for the CDD factor [6] is a special kind of function in the context of Smatrix bootstrap.For simplicity,we focus on the scattering of massive particles in integrable field theories where we only need to consider 2 to 2 scatterings.We parameterize energy and momentum in terms of rapidity

Due to Lorentz invariance,the 2 to 2 S-matrix can be written aswhere ‘i,j’ and ‘k,l’ denote the quantum numbers of incoming and outgoing particles,respectively andθ≡θi-θj.The idea of S-matrix bootstrap is to fix the S-matrix as much as possible from general physical principles and assumptions about analyticity.One requires thatsatisfy a set of bootstrap axioms such as unitarity and crossing symmetry.These axioms lead to a set of functional equations for the S-matrix.However,in general they are not sufficient to fix the S-matrix completely.If we multiplyby a scalar factor Φ(θ)

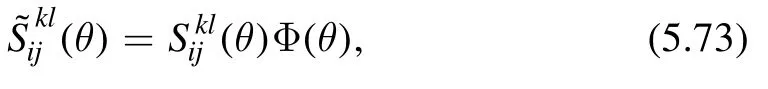
such that Φ(θ) is a meromorphic function which is analytic and bounded in the ‘physical strip’ 0 ≤ Imθ≤πand satisfeis the equations

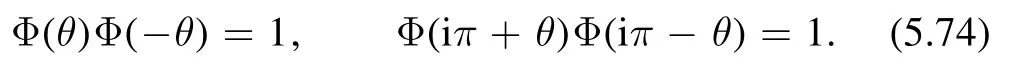
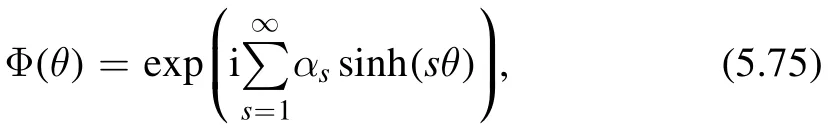
whereαsare parameters.Alternatively,it has the representation in the rational form

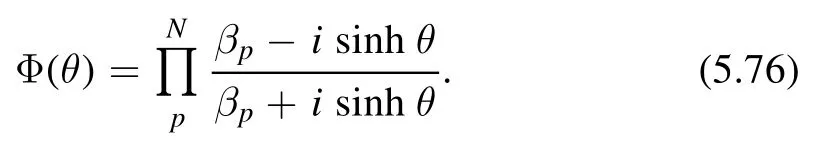
It is easy to verify that the factor from gravitational dressing can be written as

which is indeed a CDD factor in the exponential form.Although our discussion is for integrable field theories,the proposal of gravitational dressing is applicable to any S-matrix.

Effects of CDD factor.The CDD factor from gravitational dressing is quite simple.Multiplying such factors to the S-matrix has some interesting consequences which is most easily analyzed in integrable QFTs.

1.The deformed S-matrix still satisfies unitarity,crossing symmetry and Yang-Baxter equations,so it is still integrable.This implies that thedeformation should preserve integrability.This is confirmed by the fact thatdeformation preserves all the higher spin charges [1].

2.Having the deformed S-matrix,we can compute the deformed spectrum by thermodynamic Bethe ansatz.This has been done and the result is the same as the deformed spectrum we found in section 3 using factorization formula.

3.The connection between CDD factors and irrelevant deformations of CFTs was already noticed by Sasha Zamolodchikov in [42] when studying the RG flow between Ising and tri-cricial Ising.There he also found that at the leading order of perturbation theory,the corresponding operator is theoperator.In the early 90s,Alyosha Zamolodchikov studied extensively the spectrum of IQFTs that are deformed by CDD factors using TBA.He observed that for generic CDD factors,the spectrum always has a square root branch point at finite R.This singularity was also observed in [43].In general,given a CDD factor,it is not clear which irrelevant deformation it corresponds to in the Lagrangian formulation.Thedeformation and the CDD factor we found in this section provides a very neat example of such correspondences.

4.As we mentioned before,multiplying CDD factors to the S-matrix corresponds to irrelevant deformations of QFTs.Under irrelevant deformation,a QFT becomes an effective field theory and one expects that there are infinitely many terms in the Lagrangian,which is the case fordeformation.For relevant perturbation of CFTs,it is known that in general different signs of the coupling constant lead to very different IR theories.Therefore we should not be surprised that similar things happen for irrelevant deformations,which is indeed the case fordeformation.

5.2.3.Torus partition function.In this section,we explain how to compute the torus partition function directly from the path integral of 2D gravity.This calculation is rather technical and have many subtleties.We will give the idea and sketch the main steps.More details are referred to the original paper[104].Before going into any details,it is worth pointing out that the computations below are not the usual path integral that one does for 2D gravity.First of all,one restricts the path integral to torus topology.Secondly,the final result of the computation,which is thedeformed torus partition function still depends on the parameters of a fixed torus.Therefore,what the path integral really does is summing over all possible mappings from a worldsheet torus to a fixed target space torus.The mappings are restricted to have winding number 1 and the weight of the mapping is specified by the gravity action.

The first order formalism.Due to several technical reasons,in particular,to consider the system in finite volume,it is necessary to use the so-called first order formalism.In this formalism,instead of integrating over the metricgαβ,one integrates over the veilbein eaα,the spin connection ωαand a pair of Lagrange multipliersλa.Here the indicesα,β=0,1 anda,b=1,2.We write the action as

where

Notice that we put the vacuum energy term to the matter part of the action.The veilbein is defined as the ‘square root’ of the metric

whereηabis the standard metric for Minkowski spacetime.Using the veilbein,the action of the vacuum energy becomes

The action for the 2D gravity becomes

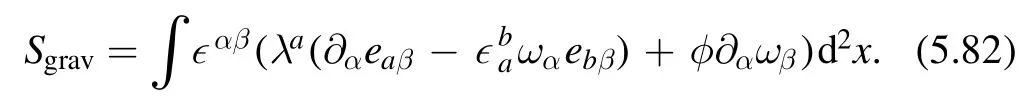
The variation with respect toλaenforces the relation between the veilbein eaαand the spin connection ωα

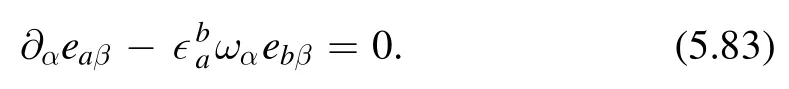
As before,a variation with respect to the dilaton φ forces the spacetime to be flat

This equation implies that we can takeωα= ∂αω.Plugging this into (5.82) and after some manipulations,one arrives at the following simple action

Furthermore,one introduces an auxiliary variable Xadefined as

By adding a total derivative term,one can rewrite the total action in the final form

This is the action that the authors of [104] propose to take in the path integral.

Partition function and integration.The partition function is now defined as

where we need to integrate over the vielbein eaαand the Lagrange multiplier XaandVdiffis the volume of reparameterization group.The idea of performing the path integral is similar to computing the one-loop vacuum energy in string theory [44].For the different variables,we decompose them to various pieces that we need to integrate over.For the vielbein,it can be shown that a generic vielbein on a torus can be decomposed in the following way

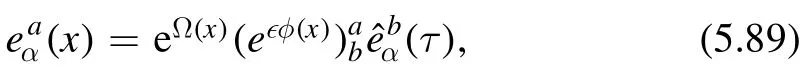
where ∈in the exponent is the Levi-Civita symbol andis a constant vielbein depending on the modular parameterτ=τ1+ iτ2given by

From this decomposition,it is clear that integrating overis equivalent to performing functional integration over Ω(x),φ(x) together with usual integral over modular parameter τ.

The quantityX a(x) can be decomposed as

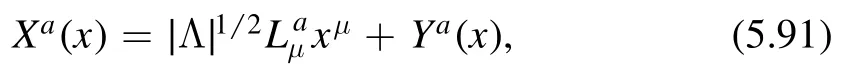
where

are the parameters that parameterize the parallelogram(or the torus) andY a(x) are scalar fields that are periodic inμx.Notice that on a torus the coordinatesμxare periodic and we can choose

So the integration overX a(x)can be traded by the integration overxμand functional integration overY a(x).

To proceed,one further decomposes the integrations over Ω(x)andφ(x)into constant part(slow)and its orthogonal part(fast) as

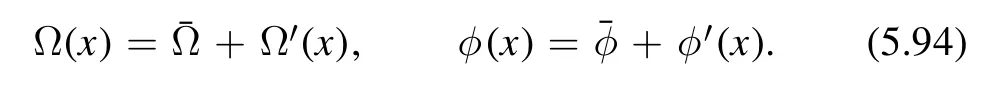
The upshot of the calculation is that,as it turns out,the functional integrals overY a(x),Ω′(x),φ′(x)can be performed and we are left with only the usual integrals over the constant partsτ,

Notice that the functionalZ0(gαβ) also depends on Ω′(x)and φ′(x),so it might seem a bit surprising that such integrals can be performed.The reason is the following.The functionalZ0(gαβ)does not depend onY a(x),so we can frist integrate outY a(x).This can be done straightforwardly.The integrand is Gaussian and the exponent turns out to be linear inY a(x)after neglecting total derivatives.Therefore the integration overY a(x)leads to certain δ-functional.Written out explicitly,the δfunctional contains the fast moving factorsδ(Ω ′(x))δ(φ′(x)),but not the constant piecesandThat's the reason why we can get rid of the functional integrals over Ω′(x) and φ′(x).

After performing the functional integrals,we are left with the following usual integral

where A is the area of the torus.We put a bar on the quantities to indicate that these are usual variables instead of functions ofxμ.The above equation looks like an integral transformation of the original partition function.The fact that we can get rid of the functional integrations and are left with only constant deformations is also consistent with random geometry point of view,where we argued that the deformation of the geometry is uniform and does not depend on the position.This can be traced back to the fact that the expectation value of theoperator is constant.

Equivalence to deformed partition sum.Now we need to show that the integral (5.95) is indeed equivalent to thedeformed partition sum.We recall that a constant vielbein can be parameterized byandwhich are four parameters.We can make a change of variables to bring the integral (5.95) to different forms For example,one interesting parameterization of the vielbein is

Intuitively,these can be seen as the parameters that specify the shape of deformed torus which we want to integrate over.Then the integral (5.95) can be interpreted as summing over all possible shapes of the torus with a specific weight.More explicitly,we have

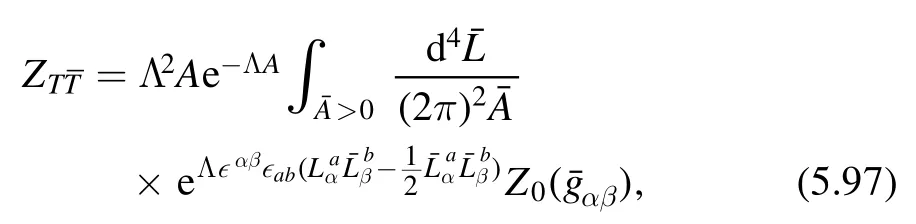
whereis the surface area of the deformed torus.This representation makes the random geometry point of view quite manifest.

To bringto a form that is closer to our discussions in section 4,we first assume that the original partition function can be written in the form of sum over Boltzmann weights

where

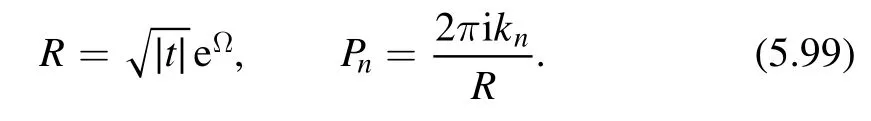
We can perform another change of variables and parameterize the torus byL1,L2,τ1,τ2by

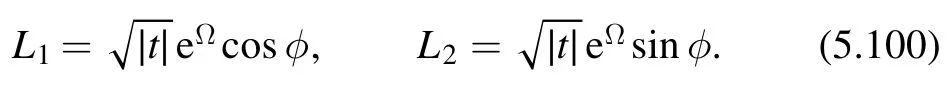
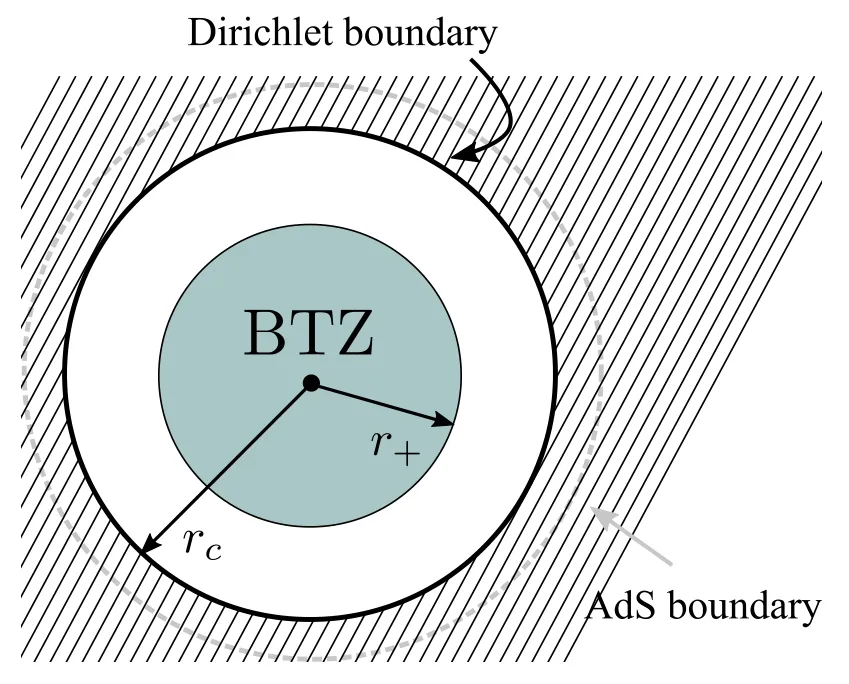
Figure 4.The cut-off geometry.Turning on deformation for the bad sign is equivalent to putting a Dirichlet boundary condition at finite radius.

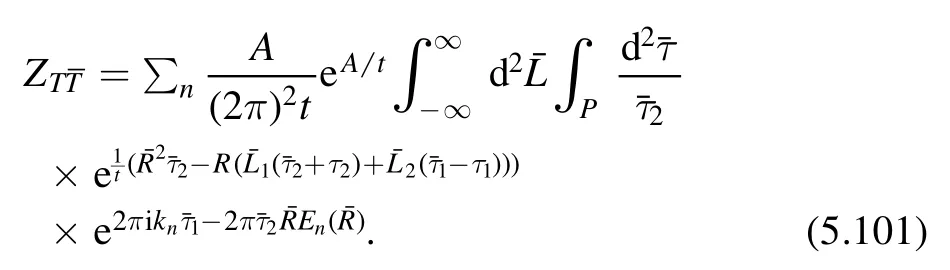
Notice that we have

Let us consider the case where the original theory is a CFT.Then the dependence ontakes a simple form

whereEnis a pure number and does not depend onThen the integral overandcan be performed since it is Gaussian and we obtain

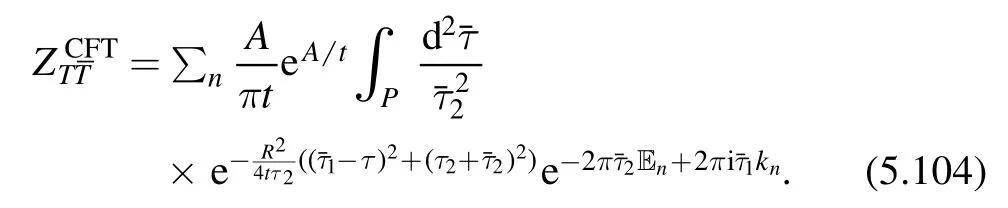
We can then perform the integration overandand obtain the expected result

whereEn(R,t)is thedeformed spectrum which we found in section 3.

5.3.Holography

Thedeformation can be defined for any 2D QFT and in particular CFTs.From AdS/CFT point of view,it is a very natural question to ask what is the holographic interpretation of thedeformation.This question was partly answered by a proposal by McGough,Mezei and Verline [17] (see also[18]).The proposal is rather simple,which is that thedeformation correspond to putting Dirichlet boundary condition in the bulk at finite radius,as is shown in figure 4.In what follows we first introduce the main proposal in more detail and then discuss some of the evidences that support this proposal.We mainly follow the paper [18] in the derivations below.

5.3.1.The cut-off picture.We give more details about the MMV proposal [17].Let us consider the action for pure gravity in AdS3space

where the second term is the Gibbons-Hawking-York boundary term.We need this term in a geometry with boundary.Different from the usual case,where the boundary is put at infinity,we put the boundary or Dirichlet wall at finite radius direction.The tensor hijis the induced metric on the boundary and Kijis the extrinsic curvature.We write the metric in the following coordinate system

In this coordinate system,the extrinsic curvature is given by

We take the AdS radius to be ℓ = 1,the Einstein equation in this coordinate system

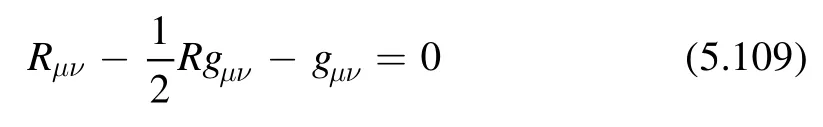
is given by

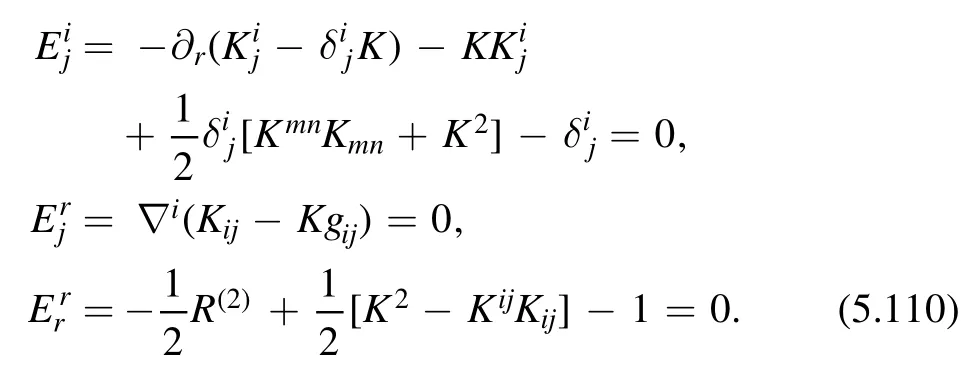
In terms of gij,the action after proper integration by parts takes the following form

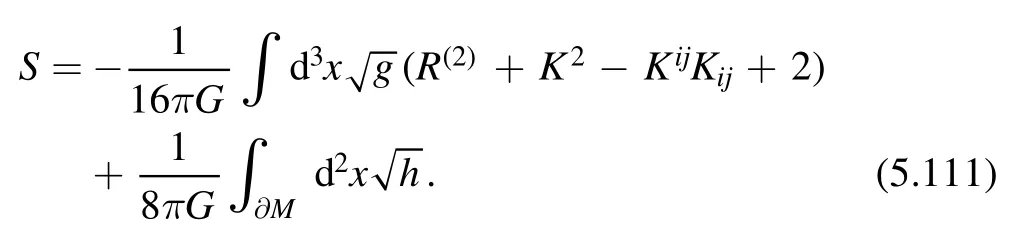
The quasi-local stress energy tensor on the boundary is defined via the on-shell variation of the action

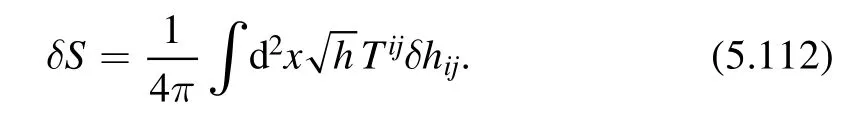
This yields the stress energy tensor of the form

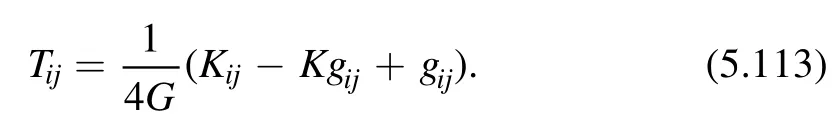
In AdS/CFT dictionary,we identify this quasi-local stress energy tensor with thedeformed stress energy tensor of the boundary theory.The crucial point is that via (5.113) the Einstein equation (5.110) can be rewritten in terms of the tensor Tij.This leads to equations about Tij.For example,the Einstein equation=0leads to the conservation of stress energy tensor

5.3.2.Trace flow equation.Now let us see what does=0 tell us about the quasi-local stress energy tensor.The trace of the stress energy tensor is

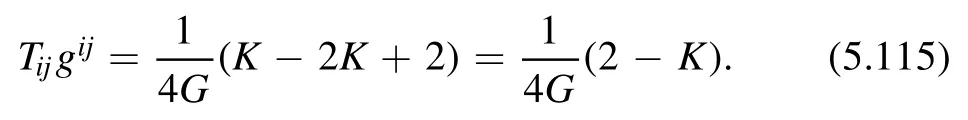
Theoperator can be written as9Here we follow the convention of [18] for the definition of operator,which is slightly different from the previous sections.

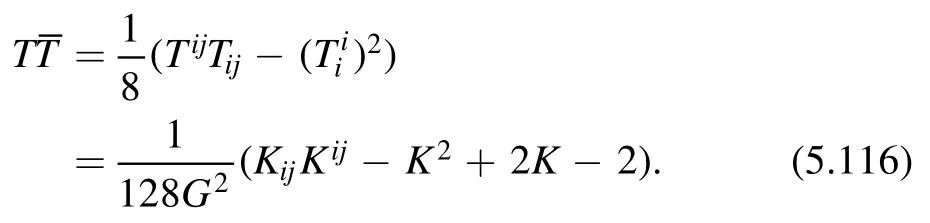
Now using the Einstein equationwe have

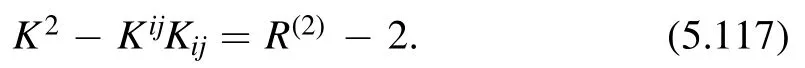
Therefore we can write

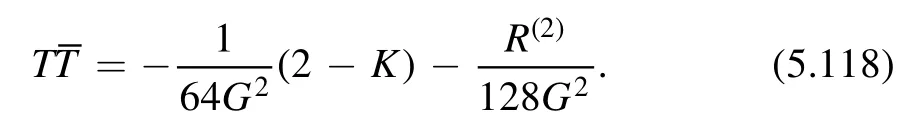
When the boundary metric is flat,we haveR(2)=0.From(5.115) and (5.118) we see that

This is the trace flow equation for thedeformed CFT which can also be derived from the boundary QFT,as we will show shortly.Notice that the discussion above is general and works for any solution of Einstein equation with flat boundary metric.

Now we derive the trace flow equation from the boundary QFT.Let us denote the action of the theory asS(t).From the definition ofdeformation,

If the theory has a single mass scale μ (which is the case for thedeformed CFT),the infinitesimal scale transformation is given by the trace of the stress energy tensor as

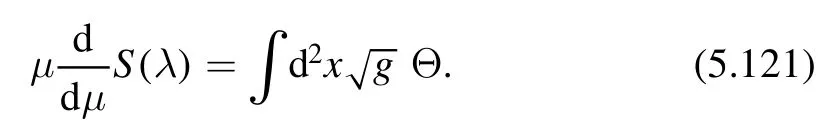
The mass scale is set by the dimensionful parameterTherefore by comparing (5.120) and (5.121),we find that

Notice that this is an operator statement and is true inside another correlation functions.We find that (5.119) and(5.122) matches exactly if we identifyt=8G.We see that the bulk and boundary derivations of the trace flow equation has very different starting points,yet they lead to the same equation.This is an evidence for the cut-off geometry proposal.

Another comment is that using the trace flow equation (5.122) and the factorization formula for the expectation value of theoperator,we can also derive the spectrum of thedeformed CFTs.Therefore,we can view the trace flow equation (5.122) as an alternative definition of thedeformation for CFTs.

The trace flow equation can be generalized to curved spacetime.For maximally symmetric spacetime with constant curvature,it is simply given by

whereR(2)is the Ricci scalar of the 2D boundary spacetime.

5.3.3.Deformed spectrum from the bulk.In this subsection,we show how to obtain the deformed finite volume spectrum from the bulk.To this end,we consider the Euclidean black hole solution.The metric of the Euclidean BTZ is given by

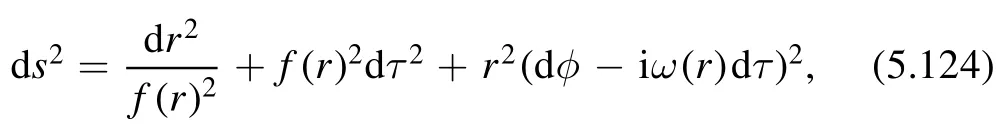
where

The quasi-local energy is given by

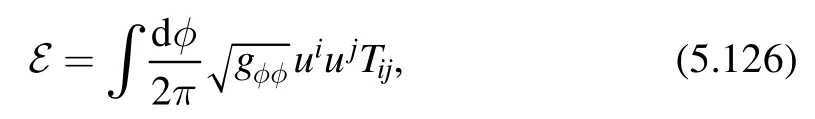
where Tijis the quasi-local stress energy tensor (5.113) andis the unit vector normal to the constant τ slice.We have

The size of the spacial circle is given by

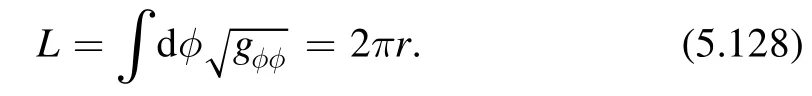
Using the prescription for the definition of the quasi-local stress energy tensor and the explicit form of the metric,we can compute the integral (5.126).The result is given by

where we have used the relationt=8G.Identifying the parameters properly,this indeed takes the form of the deformed finite volume spectrum,which constitute another strong evidence for the proposal.

Before we end this section.We make two comments about the cut-off geometry proposal.First of all,the cut-off geometry only works for the bad sign of the deformation parameter.This can be seen with the identificationt=8Gand the formula for the deformed energy (5.129).

Secondly,there are other checks which provides further evidence for the cut-off geometry.These include signal propagation speed [17],sphere partition function [21] and entanglement entropy [45,46,108].However,the cut-off geometry proposal is only valid for pure gravity sector.If there are other fields,say a bulk scalar field,then the proposal is no longer true [18,20].

6.New developments

6.1.Introduction

The contents in the previous sections constitute the lectures which the author gave in December 2018.The lecture notes were completed in March 2019.As we mentioned at the beginning,these lectures were intended for non-experts who wanted to study the subject for the first time.Therefore more emphasis is put on pedagogy instead of completeness.Due to this reason,the topics chosen in these lectures are rather limited and are mainly related to the authors own works.However,deformation has been a highly active research area in the past few years and many exciting new developments have been made since March 2019.Any attempt for reviewing a quickly developing field runs the potential danger of being out-of-dated quickly.To compensate the very limited choice of the subjects discussed so far in the previous sections,and also to keep the readers more up to date,we give a concise summary for more recent developments.By recent,we mean the developments up to January 2021.Our main goal here is to provide a convenient literature guide for the reader with some short comments.

To make the discussions more organized,we classify the developments into the following loose categories

· Generalizations.Thedeformation is a solvable irrelevant deformation for 2D relativistic QFTs in flat spacetime.It can be generalized in various directions.In fact,every word in the emphasized part have been generalized to some extent.For example,there have been attempts to generalizedeformations to curved spacetime,to non-relativistic systems,to non-QFTs,and to higher dimensions.We will summarize these generalizations in section 6.2.

· Other physical quantities.In the previous sections,we have discussed a few physical quantities including the deformed classical Lagrangian,the deformed finite volume spectrum,quantum S-matrix and torus partition function.There are many other interesting physical quantities that one would like to compute in order to gain deeper understanding ofdeformation.For example,two classes of quantities of great interest are correlation functions and quantum information measures.These quantities are typically harder to compute than the ones we have discussed,but solid progress have been made in the past few years,which will be summarized in section 6.3.

· Holography.Shortly after the original papers ofdeformation,the cut-off geometry was proposed as the holographic dual.Important developments have been made in several directions in the past few years.The first direction is refinements and further discussions of the cutoff geometry picture; the second is applying the holographic proposal to compute more physical quantities in the bulk.The last direction is going beyond the cut-off geometry proposal.It is known that the cut-off geometry proposal has serious limits such as it is valid only for one sign of the deformation parameter and only for the pure gravity sector.Therefore the cut-off geometry cannot be the whole story and alternative holographic dictionaries are called for.Developments in these directions will be summarized in section 6.4.

· Single-trace deformation.Theand other solvable irrelevant deformations we discussed so far belong to the double-trace deformations.There has been a parallel development for a closely related deformation called the single-tracedeformation shortly after the original papers ofdeformation.The single-tracedeformation is defined for orbifold CFTs,which are holographic dual of string theories onAdS3× N background.This deformation share many properties of the double tracedeformation.Moreover,it can be realized on the string worldsheet as a marginal deformation.This allows one to apply powerful worldsheet techniques to study this deformation.We will summarize some developments in this direction in section 6.5.

· String theory and 2D gravity.One of the early motivations for studyingdeformation comes from the study of effective string theory.Therefore the connections betweendeformation,string theory and 2D gravity have been expected to some extent.In particular,as we discussed in section 5,deformation of a QFT can be re-interpreted as coupling the theory to a 2D topological gravity.These important intuitions aboutdeformation have been clarified further and generalized and will be summarized in section 6.4.

We would like to emphasis that this classification is not strict because some works fall into several categories while some other works cannot be easily classified.

6.2.Generalizations

In this section,we briefly summarize the generalizations ofdeformation of 2D relativistic QFTs in various directions.All the generalizations share certain common features such as non-locality and solvability in some proper sense.At the same time,different generalizations come with their own motivations and new features.

More general bilinear deformations.deformation can be defined for any QFT with a local stress energy tensor.In this sense,it is the most general solvable irrelevant deformation.If the QFT under consideration enjoys more symmetries,it is possible to construct other solvable deformations.

The first deformation of this kind proposed in the literature is thedeformation [3].A slight variant is the very specialdeformation [47,48].A generalization of thedeformation is theJTadeformation [49].All these deformations require an additional U(1)symmetry,which is preserved along the flow of the deformation.These deformations are also irrelevant solvable deformations and are somewhat simpler than thedeformation.For example,thedeformed 2D CFT preserves one copy of the Virasoro algebra,which allows the non-perturbative computation of correlation functions [40].In addition,we can combineanddeformations and define a more general jointdeformation.This joint deformation is obviously more complicated,yet it is still solvable.For example,the deformed spectrum [50] and torus partition function [51,52] have been studied.

For integrable QFTs and 2D CFTs,there are even more possibilities because these theories possess an infinite tower of conserved currents.Irrelevant deformations triggered by operators which are constructed from higher conserved currents have been discussed in the original paper by Smirnov and Zamolodchikov[1].Such deformations have been studied further in [4] for CFTs and in [54,53] for integrable QFTs.

Yet another interesting additional symmetry is supersymmetry.deformation of supersymmetric QFTs have also been studied in [55-62] for different numbers of supercharges.

Other spacetimes.The originaldeformation is defined for QFTs in 2D flat spacetime.Therefore it is natural to ask whether we can definedeformation for QFTs on curved spacetime and in higher dimensions.

The generalization ofdeformation to curved spacetimes at the classical level is straightforward.The deformed classical Lagrangian on curved spacetime was first derived in[10] and later found by different approaches in [63].At the quantum level,it is easier to consider the large central charge limit where the large c factorization ensures the factorization of the expectation value of theoperator,which underlies the solvability of the quantum theory.One important application in this limit is the calculation of partition functions for maximally symmetric spaces by using the trace flow equation[21,45].An interesting deformation which is related but different from thedeformation can be defined in the context of dS/dS correspondence [64].It is more difficult to take into account finite c corrections.The factorization property of the expectation value ofoperator is studied[65,66].A definition ofdeformation in curved spacetime inspired from 3D gravity is proposed in [67].

The generalization ofdeformation to higher dimension is basically an open question.One of the reason that,even before any kind of-like solvable deformation,there are very few examples of higher dimensional QFTs that are solvable apart from free theories.Therefore,defining a ‘solvable’ deformation for generic higher dimensional QFTs seems a bit pointless.One possibility is to focus on certain specific theory that is solvable,and try to define a solvable deformation similar todeformation.One of the most interesting theories of this type is theN =4 SYM theory,which is integrable in the planar limit.An interesting irrelevant deformation ofN =4 SYM is proposed in [68].The possible string theory dual are discussed in [69,70].

Specific theories.It is also interesting to studydeformation for specific models,although strictly speaking,these studies are not‘generalizations’ofdeformation.The specific models that have been studied underdeformation include chiral bosons [71,72],compactified boson [73],WZW model [74],Sinh-Gordon models [11],Heisenberg model [75],large N vector model [76],2D VA model [77],Liouville related theories[78,79],2D dilaton gravity[80]and the 2D Yang-Mills theory [81-84].

Beyond relativistic QFTs.and other deformations have been generalized beyond relativistic QFTs.The first generalization is to non-relativistic QFTs [85-90] where one does not assume Loretnz invariance.Similar deformations can be defined even for non-QFTs.Examples include quantum mechanics [91-93],quantum integrable spin chains [94-96]and the 1D Bose gas[97].Deformations which are analogous but different fromdeformation have also been considered.These include DBI action analogue [98] and nonlinear electrodynamics [99].

6.3.Other quantities

I n the previous sections,we have discussed several physical quantities ofdeformed theories.In the past few years,more quantities have been studied.Most notably,correlation functions of local operators and quantum information measures such as entanglement entropies.

More on torus.Before moving to the discussion of new quantities,let us mention that there have been more progress on torus partition functions and thermodynamics of the deformed theories.The torus partition function has been computed perturbatively in [100].Deformation of KdV charges was first studied in [101]and later generalized to the torus case in [102].Some general comments on thermal instability is given in [103].An elegant method to obtain the torus partition function for theand more general+deformed CFTs via integral transformation have been proposed.The integral transformation method fordeformation first appeared in [104] from 2D gravity proposal.Later it was developed largely in the single trace deformed theories [105-107] where the integral kernels were derived from worldsheet techniques.Due to universality,the results are also applicable to the double trace deformations.An alternative derivation for the integral kernel based on 3D gravity perspective similar to [104] is given in [51].

Quantum information measures.Quantum information has played an important role in recent developments of theoretical physics.It is therefore a natural and interesting question howand other solvable irrelevant deformations affect quantum information measures.The most widely studied measures are the Rényi and entanglement entropies.Thedeformed entanglement entropy was first studied in [45]and further developed in [108-111] on a spherical geometry in the large c limit.Perturbative calculations of the Rényi and entanglement entropies have been performed in [112-115].Holographic computations ofdeformed quantum information measures and their implications have been studied further in [111,116-123].Another important quantum information measure,the holographic complexity have been studied in [124-128].

Correlation functions.Correlation functions are much more complicated than spectrum or partition functions,even in the undeformed theories.Correlation functions fordeformed CFTs was first studied in the large c limit in [31].The correlation functions for thedeformed CFTs was first considered in[40].An important non-perturbative result is the flow equation for thedeformed correlation functions,which was first derived in [129].It was later derived from a different approach in [130].Perturbative calculations based on conformal perturbation theory to the first order for theanddeformations have been performed in [131-135].Perturbative calculations based on Feynmann diagrams have been studied in [169,170].

Other aspects.Another interesting direction is to consider physics out of equilibrium.Quench dynamics has been considered in[136,137]fordeformed CFTs.Finally,it is important to understand how symmetry algebra deforms underand related deformations,especially for deformed 2D CFTs.This will shed new lights on solvability of the deformations.The deformed classical algebra for,are considered in [138,139].

6.4.Holography

The cut-off geometry picture was first proposed in[17].It was further refined and developed in [18-20,28,30,140-142].This proposal is very intuitive and attracted a lot of interest.Due to its simplicity,one can apply it readily to compute various quantities in the bulk and compare with the boundary results.Works in this direction include [122,143-147].

The cut-off geometry proposal has a number of shortcomings.It only works for pure gravity sector,and it only works for one sign of the deformation parameter.From general principles of AdS/CFT,one expect thatanddeformations,being double-trace deformations,should correspond to a change of the boundary conditions.The proposal in this direction was first formulated for thedeformation[41] and later generalized to thedeformation [148].Another holographic proposal based on random geometry picture was given in [149].

6.5.Single-trace deformations

Soon after the proposal ofdeformation.It was realized that in the context of holography of AdS3,one can define a single tracedeformation [23].Such deformation is defined for orbifold CFTs where one needs to take N copies of a CFT.From the stress tensor of the each copy,one can define twooperators for the orbifold theory.One is the usual double-traceoperator,and the other one is the single traceoperator which triggers the single-tracedeformation.

From general principles of AdS/CFT,double trace deformations modify the boundary conditions and do not change the bulk geometry.On the other hand,single trace deformations do change the bulk geometry.Therefore,we expect that the singe tracedeformation modifies the bulk geometry,which is indeed the case.The undeformed orbifold CFT corresponds to strings on AdS3geometry.It is found that for one sign of the deformation parameter,the deformed geometry on which the strings propagate interpolates between AdS3in the IR and a linear dilaton space in the UV.This geometry is the two dimensional vacuum of the little string theory [23].For the other sign,the resulting bulk geometry has curvature singularity at finite radius.The single tracedeformation is dual to a marginal deformation on the string worldsheet,which is pointed out in [22].This deformation has been studied further in parallel to the double tracedeformation.Many physical quantities have been computed,such as correlation functions [24,29],entanglement entropy[25],holographic Wilson loops [26] and complexity [128].Generalizations to the case with conformal boundaries have been considered in [150,151].String dynamics for such theories are studied in [152-154].The relation between the single tracedeformation and the TsT transformation was pointed out in [155,156].

6.6.String theory and 2D gravity

As we discussed in section 5,deformation of a QFT is equivalent to coupling the theory to a 2D topological gravity [9,104].This intuition was further clarified in [168]where the 2D topological gravity is identified with massive ghost free dRGT theory in 2D.Generalization of the 2D gravity interpretation to curved spacetime has been discussed in [63,168].Such an interpretation is also valid for thedeformation of non-relativistic QFTs [88].The difference is that the gravity theory is the 2D Newton-Cartan geometry.It is also pointed out in [88] that for non-relativistic QFTs one can actually define three fundamental solvable deformations includingdeformation,all of which have gravity interpretations.

A related interpretation of thedeformation is that it can be seen as a dynamical or field dependent change of coordinates.This was first pointed out in[9]from 2D gravity interpretation.Later is was derived from a different perspective in [39] which was mainly motivated from integrability.The dynamical change of coordinate point of view was further clarified in[63]and generalized to the non-relativistic set-ups in [86,88,89].

Acknowledgments

It is a pleasure to thank Ofer Aharony,Shouvik Datta,Amit Giveon and David Kutasov for collaborations on the relevant projects that lead to this review.I thank Gang Yang for kind invitation and hospitality at ITP-CAS.I’m also indebted to Luis Apolo,Wei Li,Pujian Mao,Wei Song,Junbao Wu and Gang Yang for various helpful discussions.

Many thanks to Alex Belin,Shouvik Datta,Amit Giveon,Madalena Lemos,Kostas Siampos,Wei Song,Roberto Tateo,Junbao Wu and Gang Yang for valuable feedbacks.