计及分布式电源不确定性的配电网概率潮流计算

贾向恩，宁永龙，顾勇

(国网吴忠供电公司，宁夏 吴忠 751100)

0 引 言

随着能源短缺和环境污染问题的日益突出，可再生清洁能源获得了人们的广泛关注和重视[1]。分布式电源在配电网的渗透率越来越高，但其出力的不确定性会给配电网的运行带来严重的影响，而配电网概率潮流计算是评估配电网运行不确定性及安全稳定性的有效工具[2]。为保障配电网运行的安全稳定和促进分布式电源的健康发展，需对含分布式电源的配电网进行概率潮流计算分析。

概率潮流计算方法主要包括：模拟法、解析法和估计法。模拟法主要为蒙特卡罗法[3]，该方法计算结果最为准确，但计算量大、耗费时间长，且易出错，实用性较差，因此一般用它来衡量其他方法的准确性。解析法主要为半不变量法[4]，其主要思想是通过解析计算来求出系统状态变量的概率分布，该方法计算简单，但精度较差。估计法主要有两点估计法[5]，它利用输入随机变量的统计信息来逼近系统状态变量的数字特征，计算速度快，但计算精度不够理想。近年来，部分研究人员将智能算法用于概率潮流计算。文献[6]采用BP神经网络来求解不同网络状态下概率潮流的输出，但该模型训练时间较长，且计算结果不稳定。文献[7]利用无迹变换算法将概率潮流问题转化为少量样本点的确定性潮流，然后利用内点法进行求解，但在处理高维不确定性问题时效果较差，且时效性不理想。

本文提出了一种结合小波神经网络和改进无迹变换法的配电网概率潮流计算方法，通过含分布式电源配电网系统的概率潮流计算对比分析，验证了本文方法的有效性和优越性。

1 分布式电源潮流计算概率模型

1.1 分布式光伏出力概率模型

分布式光伏发电主要由太阳能电池板将太阳能转化成电能，其出力主要与光照强度相关，而光照强度r具有不确定性，其概率密度函数为[8]：

(1)

式中：rmax为最大光照强度;Γ为Gamma函数;α、β为函数的形状参数。

当光照强度均值μ和标准差σ为已知时，可获得形状参数α、β的值。

(2)

(3)

分布式光伏由一系列太阳能电池板组成，电池板的数目为M。假设每个电池板的面积和光电转换效率为Am和ηm，m=1, 2,…,M，则分布式光伏的有功出力PPV为：

(4)

由式(1)和式(4),分布式光伏的出力的概率密度函数可表示为：

(5)

式中：Rm为分布式光伏的最大有功出力值。计算表达式为：

(6)

1.2 分布式风电出力概率模型

分布式风电的出力主要由风力发电机将风能转换成电能，其出力大小主要与风速相关，而风速具有典型的不确定性。风速v的概率密度函数为[9]：

(7)

式中：α和β为函数的形状参数和尺度参数。

分布式风电的有功出力PW与风速v之间的函数关系为：

(8)

(9)

(10)

式中：Pr为额定功率值;vr、vc、vt分别为风机的额定风速值、切入风速和切出风速。

分布式风电有功出力PW函数曲线如图1所示。

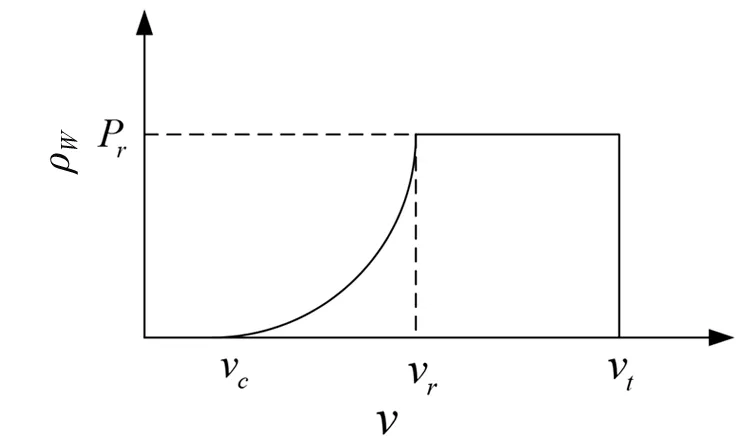
图1 分布式风电功率特性曲线

由式(7)和式(8)，分布式风电的出力的概率密度函数可表示为：

(11)

2 配电网概率潮流计算方法

2.1 小波神经网络模型

小波神经网络是一种将小波变换理论与神经网络有机结合的新型前馈型网络[10]。与传统神经网络相比，小波神经网络具有更加优良的时频局部性能和非线性映射性能。配电网潮流方程的求解较复杂，可利用小波神经网络进行有效求解，以得到输出变量的均值以及相应的权重。小波神经网络结构示意图如图2所示:X、Y分别为输入变量和输出变量;Wi、Wj分别为输入层到隐含层和隐含层到输出层的权值。

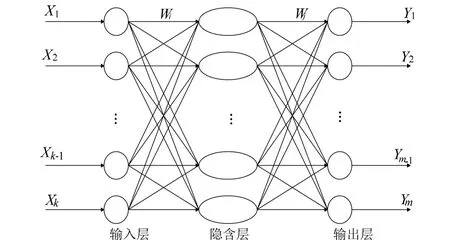
图2 小波神经网络结构示意图

隐含层中的小波激活函数选用Morlet函数，隐含层的表达式为：

(12)

其中

ψ(x)=cos(1.75x)·e(-x2/2)

(13)

式中：k为输入层的节点总数；aj、bj为网络的伸缩、平移参数。

小波神经网络的输出可表示为：

(14)

式中：l为隐含层的节点总数。

2.2 改进无迹变换理论

无迹变换通过非线性转换来传递输入变量的均值和协方差信息，从而获得输出变量的概率密度分布[11]。假设X=[X1,X2,…,Xn]T为n维随机变量，协方差矩阵为PXX，对输入分布上精选样本点的位置进行选取，组成Sigma向量矩阵χ的方法如下。

χ0=m

(15)

(16)

(17)

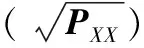
每组样本点对应的权重值计算方法如下：

(18)

输出变量Y由Sigma向量通过非线性转换获得，其表达式为：

Yi=f(Xi)i=0,…,2n

(19)

(20)

(21)

无迹变换算法计算简单、容易实现，且选取的样本点具有随机变量间Pearson相关性信息，但无迹变换法在处理高维不确定性问题时，会出现样本点逐渐偏离平均值的现象，导致计算精度较差。本文利用比例伸缩因数α(0<α≤1)来灵活调节样本点与均值的距离，以克服样本点的离散效应，改进后的样本点选取方法为：

(22)

(23)

对应的权重值计算方法为：

(24)

2.3 配电网概率潮流计算方法

本文结合小波神经网络和改进无迹变换算法的配电网概率潮流计算方法,利用无迹变换计算输入的Sigma向量及对应的权重值，再利用小波神经网络模型来对潮流非线性方程进行求解。主要流程为：

(1)根据式(22)和式(23)选取2n+1个采样点，根据式(24)得到与每个X对应的权重值。

(2)对于每个采样点，将其代入式(19)，然后进行以下计算。

① 在式(19)的可行域内，生成随机变量Xi。

② 根据映射函数f，由向量Xi求得向量Yi。

③ 以Yi为输入变量，Xi为对应的输出变量，对小波神经网络进行训练。

④ 输入向量Y*到小波神经网络模型，输出向量X0，并选取输入变量的最远中心，将对应该中心的输出组成集合作为计算步骤③的替换集。

⑥ 若步骤⑤获得的Y0比Yi更接近Y*，则将(Y0,X0)替换为(Yi,Xi)，然后再继续进行步骤②。

(3)根据式(20)和式(21)求取每个输出向量的均值和协方差。

3 配电网概率潮流实例分析

3.1 系统算例

本文以IEEE-25节点系统作为测试系统，节点2、节点19分别接入一组分布式光伏DG1和分布式风电DG2，额定功率均为200 kW，系统其余参数详见参考文献[12]，改进后的系统结构图如图3所示。本文采用期望值偏差εμ和标准差偏差εσ来评估算法的潮流计算性能，计算公式如下：

图3 IEEE-25节点系统图

(25)

(26)

式中：μMCS、σMCS为蒙特卡洛法获得的参考期望值和标准差；μ、σ为其他算法的期望值和标准差。

3.2 潮流计算结果对比分析

分别采用蒙特卡洛法、两点估计法和本文算法进行概率潮流计算分析。获得的节点5电压幅值U5、线路6-7的有功P6-7和无功Q6-7的均值μ、标准差σ以及计算耗费时间,如表1所示。节点5电压概率密度曲线如图4所示。系统各节点有功功率和无功功率的期望值偏差εμ、标准差偏差平均值εσ如表2所示。

图4 节点电压概率密度曲线

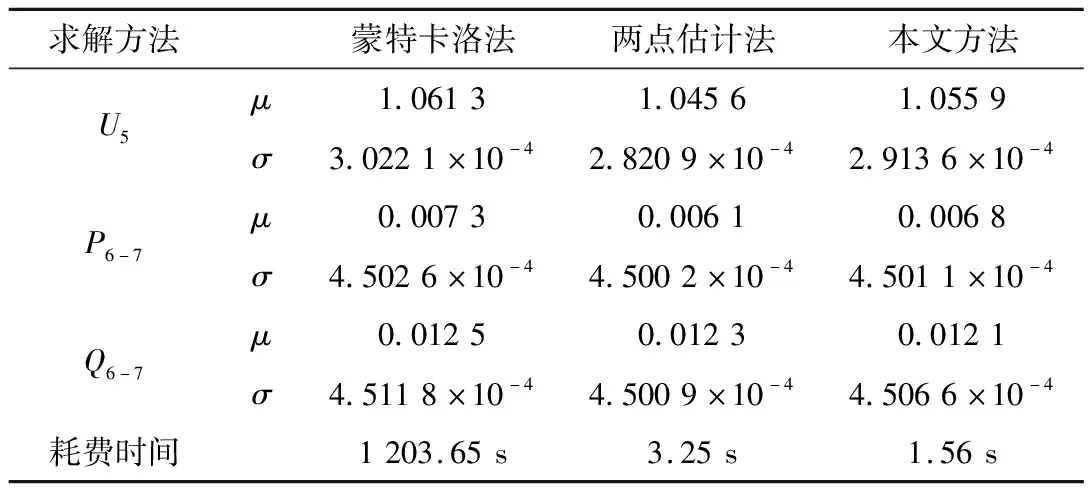
表1 概率潮流计算结果

由表1、图4和表2的结果可知，本文概率潮流算法比两点估计法的精度更高。本文方法求取的期望值偏差、标准差偏差平均值都小于两点估计法，均值μ、标准差σ与蒙特卡罗法更加接近，获得的节点电压概率密度曲线也与蒙特卡罗法更加接近，本文方法潮流计算耗费的时间为1.56 s，与蒙特卡罗法相比要快得多，且比两点估计法更快，测试系统计算结果验证了本文方法的有效性和具有的优势。

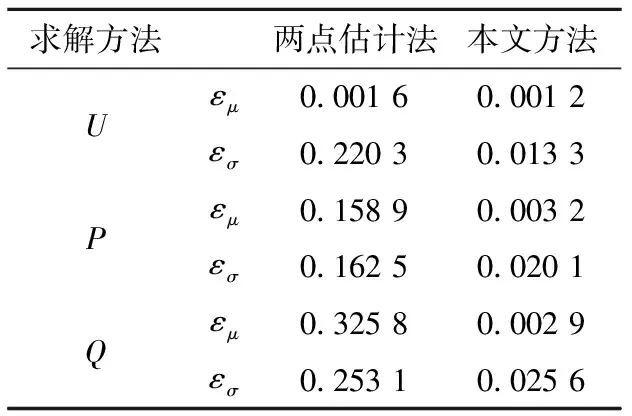
表2 潮流计算性能评价指标结果

4 结束语

本文提出了小波神经网络和改进无迹变换法相结合概率潮流计算方法，对IEEE-25节点系统的计算结果进行分析。结果表明，本文方法计算结果精度较高，求取的电压、有功功率和无功功率的均值、标准差及节点电压概率密度曲线均与蒙特卡罗法接近，本文方法计算效率较高，耗费的时间远低于蒙特卡罗法。本文结合小波神经网络和改进无迹变换法的配电网概率潮流计算方法具有很好的时效性，可为分布式电源并网后的配电网运行分析提供有效的技术参考和指导。