基于差分进化粒子群神经网络的用户侧储能容量优化配置

兰国龙，陈佳桥，叶恒志，陈旭海, 廖宝文

(1.中国水利水电第四工程局有限公司,北京 100071；2.中国电建集团福建省电力勘测设计院有限公司,福建 福州 350003)

0 引 言

随着智能电网和能源互联网的发展，电力系统对储能[1]的需求日渐增大。电化学储能以其灵活和动态响应快速的特点广泛应用于电力系统的发电、输电、配电和用电等各环节，其多重运行效益和经济价值日益凸显。

用户侧储能的应用需要解决经济性及循环寿命的问题，现有研究主要包括以下三个方面：一是储能容量配置优化与经济性分析[2-3]，通过建立用户侧储能应用的成本收益分析模型，分析储能投资的经济性，确定最佳的容量配置与运行方案，现有工作主要考虑的收益类型包括削峰填谷及需量控制；二是系统能量管理与优化控制[4]，在储能系统接入后，需要考虑与电网及终端用户系统的其他设备，如分布式可再生能源发电和负荷等，共同协调运行，以优化电池储能的实际收益，另外需要考虑对多个储能系统间的充放电功率分配及均衡控制，提高电池效率及使用寿命；三是储能应用领域[5-6]的拓展，通过增加用户侧储能系统的功能与服务类型，提高储能应用的收益。

目前储能系统成本较高，本文采用差分进化-粒子群算法对用户侧储能进行优化配置，弥补了差分进化算法搜索速度慢和粒子群算法[7]易出现局部最优的缺陷，在保证系统运行可靠性的同时，有效降低系统运行成本，提高系统经济性。

1 用户侧储能模型建立

1.1 储能系统运行目标

配置储能系统的主要目的是为运营商带来经济上的收益。本文针对峰谷价差套利对储能系统功率容量及控制策略进行优化配置。

1.2 约束条件

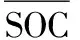
-Pn≤Pc(t)≤Pn

(1)

SOC(t+1)=SOC(t)-Pc(t)Δt

(2)

(3)

根据国家发展改革委关于两部制电价用户基本电价执行方式的通知:Pzb为主变容量；P1为容量电费;P2为需量电费；Pload为负荷功率；PN为基本电量；Pneed为需要功率；Qsurplus为剩余容量；Zn为额定容量。

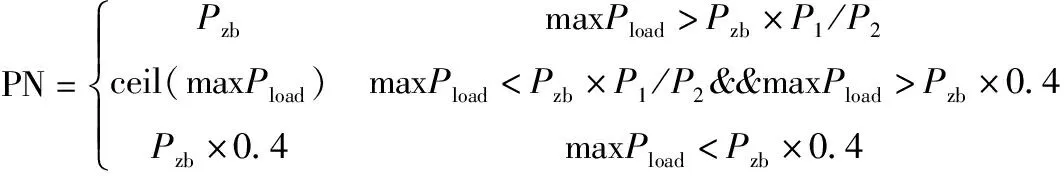
(4)

Pc=min([Pneed,Qsurplus/Δt,Pn])

(5)

Pneed=PN-Pload

(6)

Qsurplus=Zn-Q(t)

(7)

储能控制策略如图1所示。

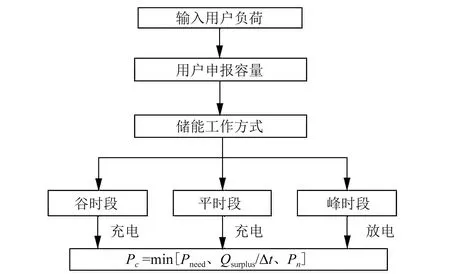
图1 用户侧储能控制策略

2 差分粒子群算法

2.1 差分进化算法

差分进化算法通过把种群中两个随机选择的不同个体加权差向量，加到第三个个体上，以此“变异”操作来产生新的目标个体；再通过“交叉”产生试验个体；最后“选择”适应度函数值较小的个体，为下一代的目标个体。种群中所有个体都需进行以上操作，实现个体进化。

对D维目标个体xi,G(i=1,2,…,NP)，变异操作如下。

vi,G+1=xr1,G+F·(xr2,G-xr3,G) (r1≠r2≠r3≠i)

(8)

式中：D为个体维度；i为个体在种群中的序列；G为进化代数；NP为种群大小；r1、r2、r3为随机选择的序号且互不相同；F为变异算子。

2.2 粒子群算法

在粒子群算法中，每个粒子以一定的速度在解空间运动，同时向自身历史最佳位置和领域历史最佳位置聚集，通过每一次的叠代，实现个体的进化。

在一个D维目标搜索空间，有N个粒子组成的群体，粒子根据式(9)～式(10)更新自身速度与位置：

vij(t+1)=w×vij(t)+c1r1[pij(t)-xij(t)]

+c2r2[gj(t)-xij(t)]

(9)

xij(t+1)=xij(t)+vij(t+1)

i=1,2,…,N;j=1,2,…,D

(10)

式中：x为第i个粒子位置；v为第i个粒子速度；p为第i个粒子最优个体位置；g为D维全局最优位置;r1和r2为学习因子;c1和c2为[0,1]范围内的均匀随机数;w为惯性权重，表示粒子对当前速度继承能力。粒子群算法流程如图2所示。

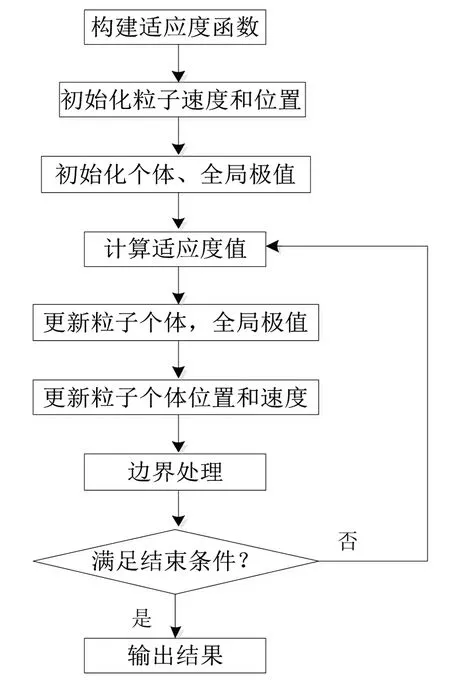
图2 粒子群算法流程图

2.3 差分-粒子群优化算法

如图3所示，差分进化算法具有较强全局最优解的搜索能力，鲁棒性强，但要获得精确度高的解，需要较多的时间。粒子群算法收敛速度快，但控制参数对算法性能影响较大，且算法早期速度快，易出现早熟现象。

因此本文提出混合差分算法和粒子群算法的优化算法，通过改进粒子更新自身速度和位置公式(9)，以综合两种算法的优点，避免算法早熟。

vij(G+1)=w·vij(G)+c1r1[xi(G+1)-xij(G)]

(11)

式中：x为第i个粒子位置；v为第i个粒子速度；c1为学习因子；r1为[0,1]范围内的均匀随机数；w为惯性权重；xi(G+1)为经过差分优化的全局最优位置；G为进化代数。

3 仿真验证

建立储能系统功率容量配比的数据库如图3所示，并在送入网络训练前，进行数据归一处理。在BP神经网络训练中，网络初始权重经由差分-粒子群算法优化得到，输入层至隐含层活化函数为tansig，输出层为purelin。

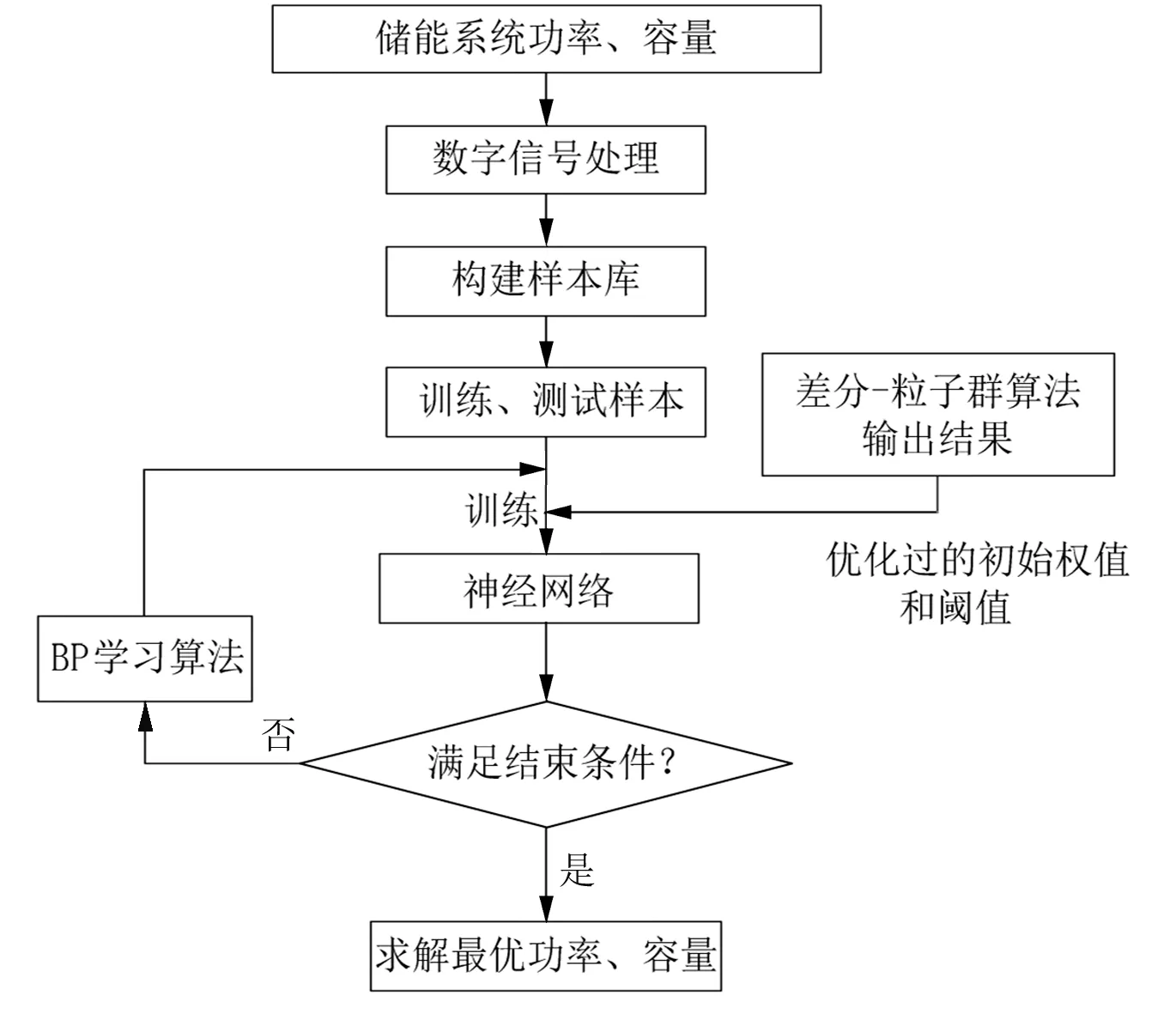
图3 储能容量优化配置流程

由图4可见，算法进化方向由适应度函数最小值方向搜索，即预测样本与期望值的误差矩阵范数最小。图5～图8为神经网络训练误差曲线，经过差分-粒子群混合算法优化改进的网络MSE(均方误差)值更小，网络训练效果得到了较大的提升。

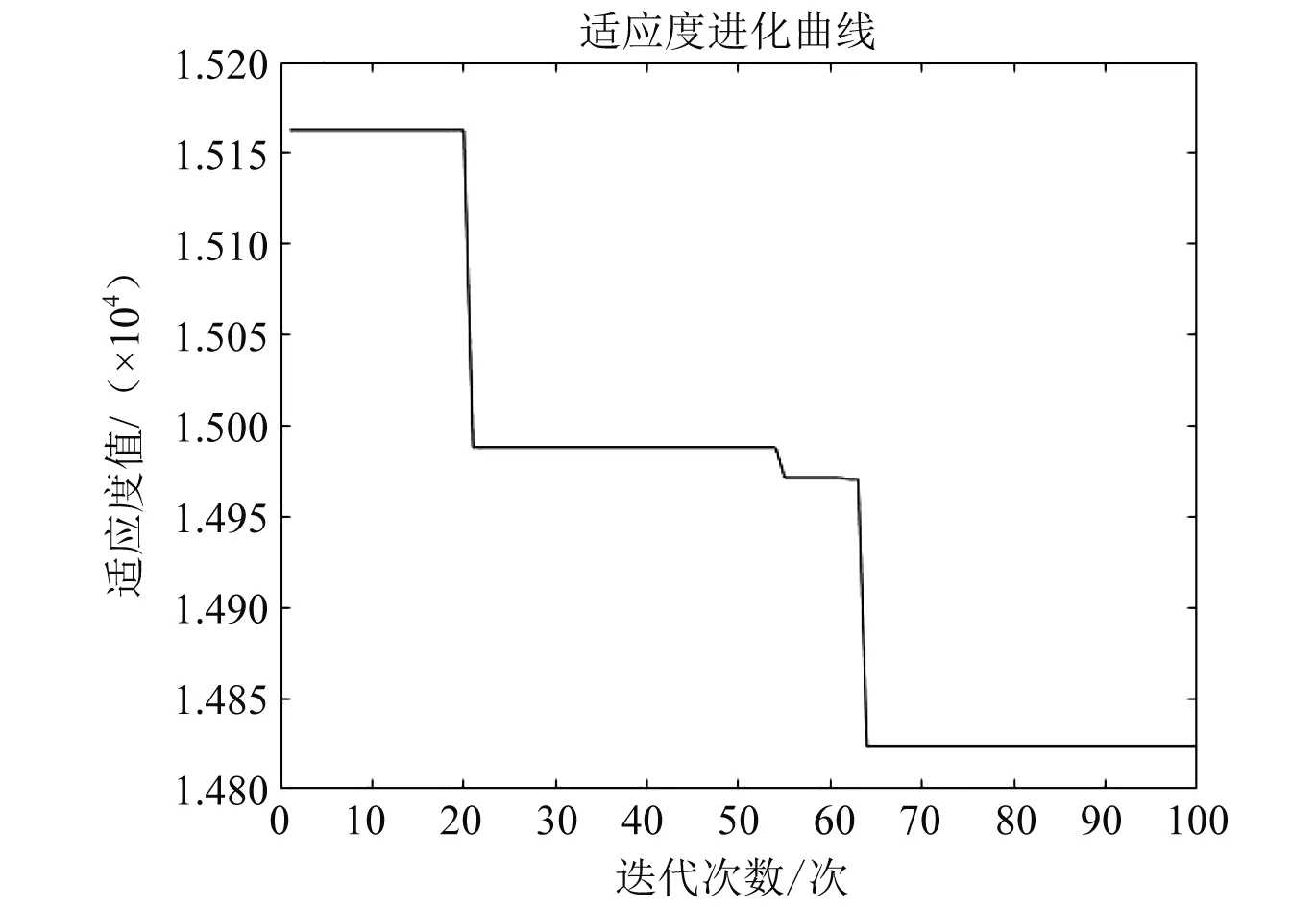
图4 差分-粒子群适应度进化曲线

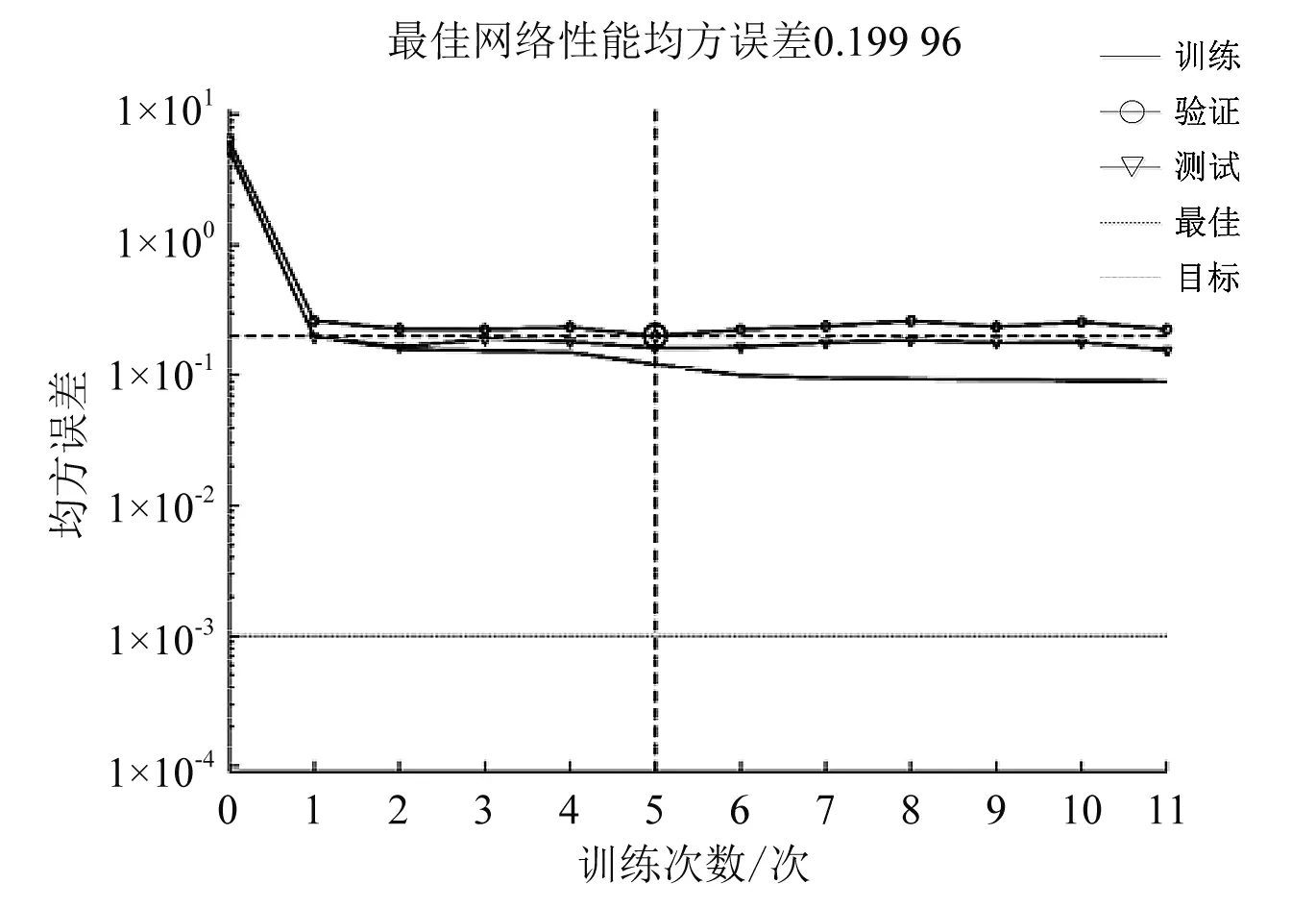
图5 随机初始权值与阈值训练误差曲线

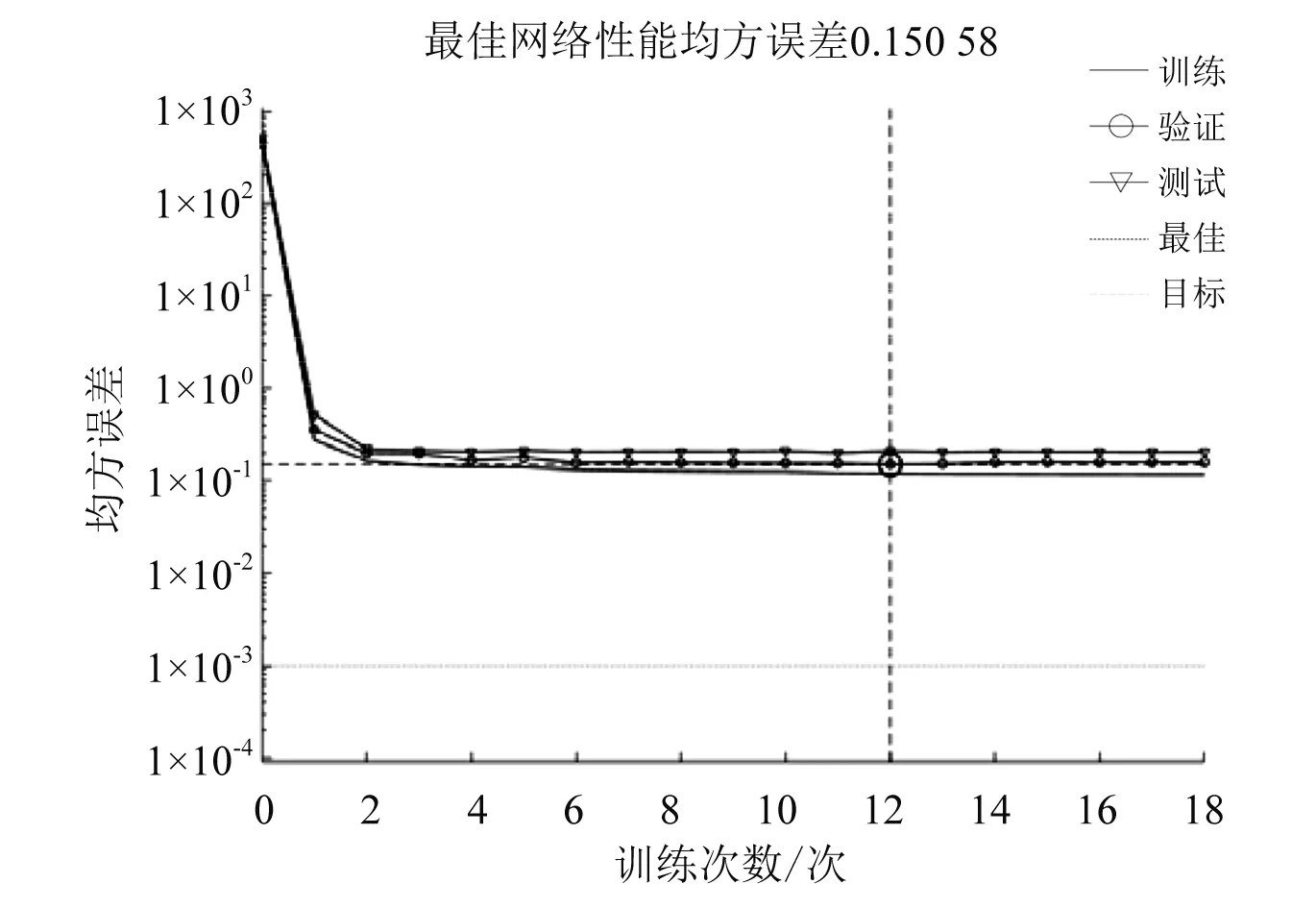
图6 粒子群优化初始权值与阈值训练误差曲线

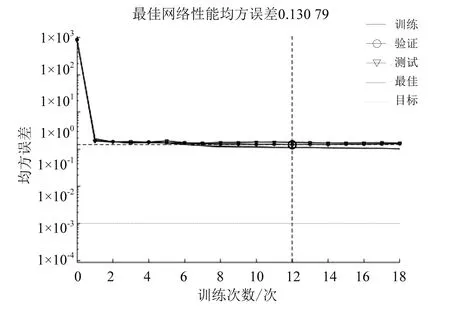
图7 差分进化优化初始权值与阈值训练误差曲线

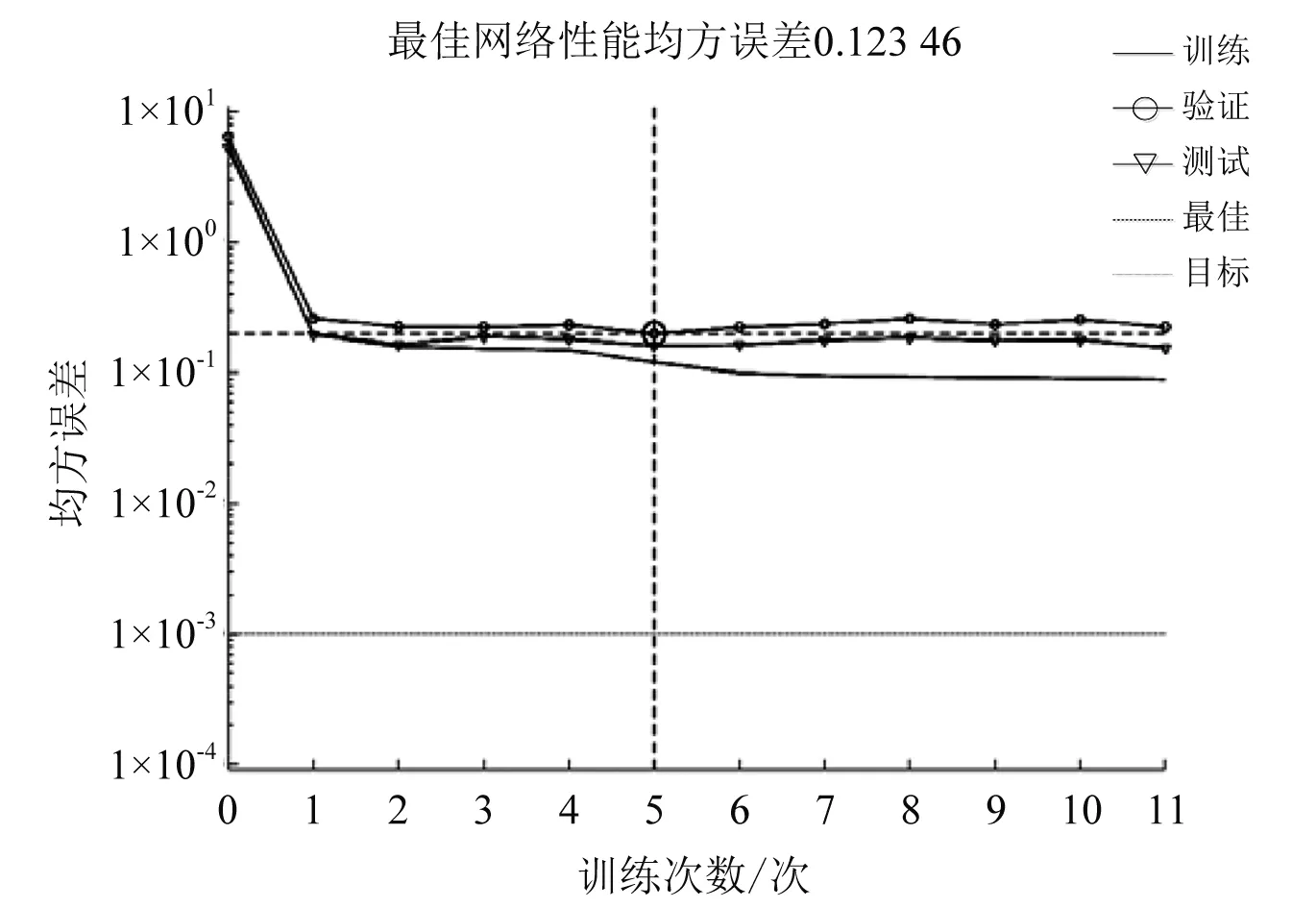
图8 差分-粒子群优化初始权值与阈值训练误差曲线

图9～图12为网络训练拟合结果，图中R称为可决因数，其值越接近1，则说明网络模型性能越好。仿真结果表明，经过差分-粒子群优化的BP神经网络的仿真结果更加向真实值聚集。

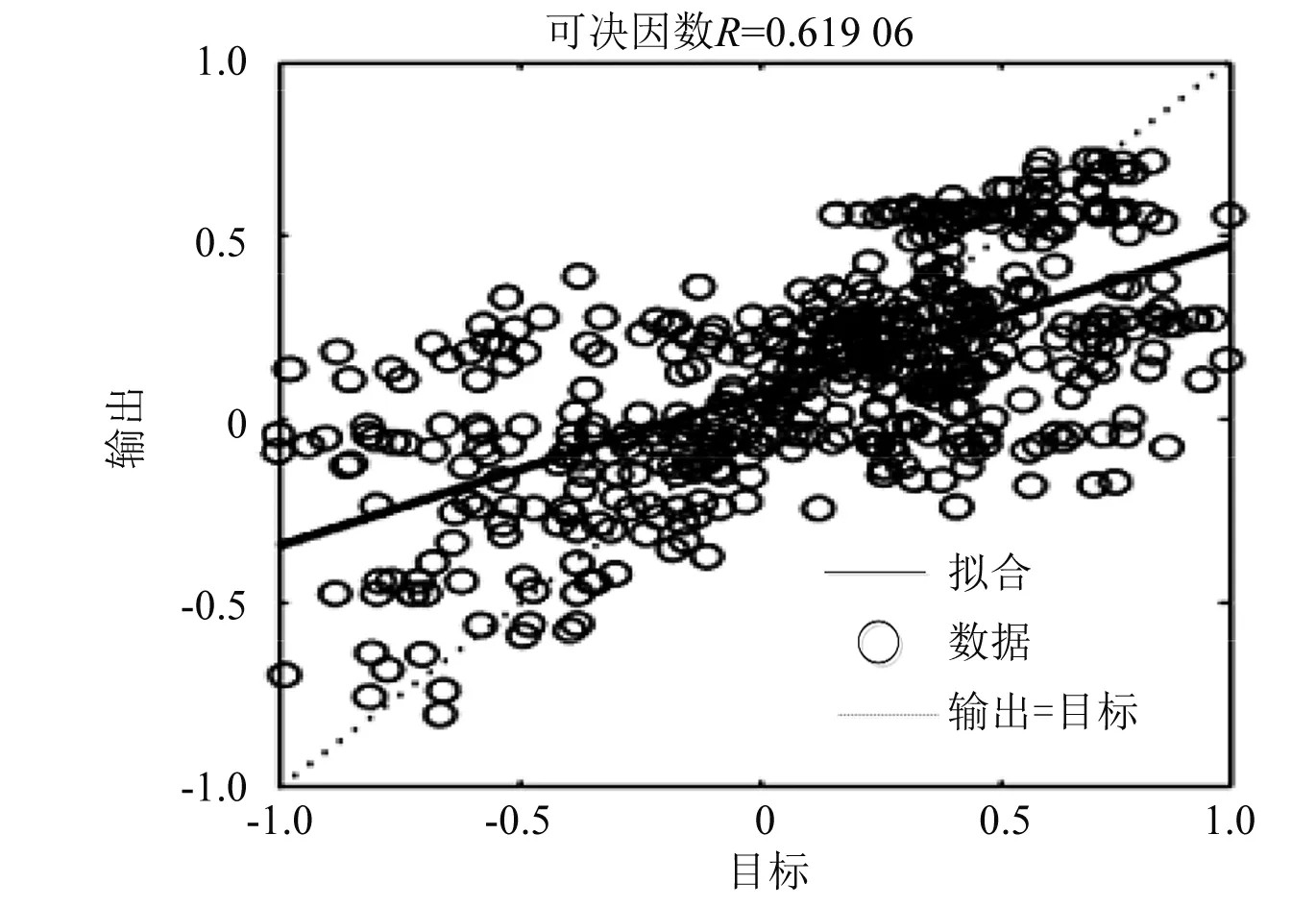
图9 随机初始权值与阈值网络训练拟合结果

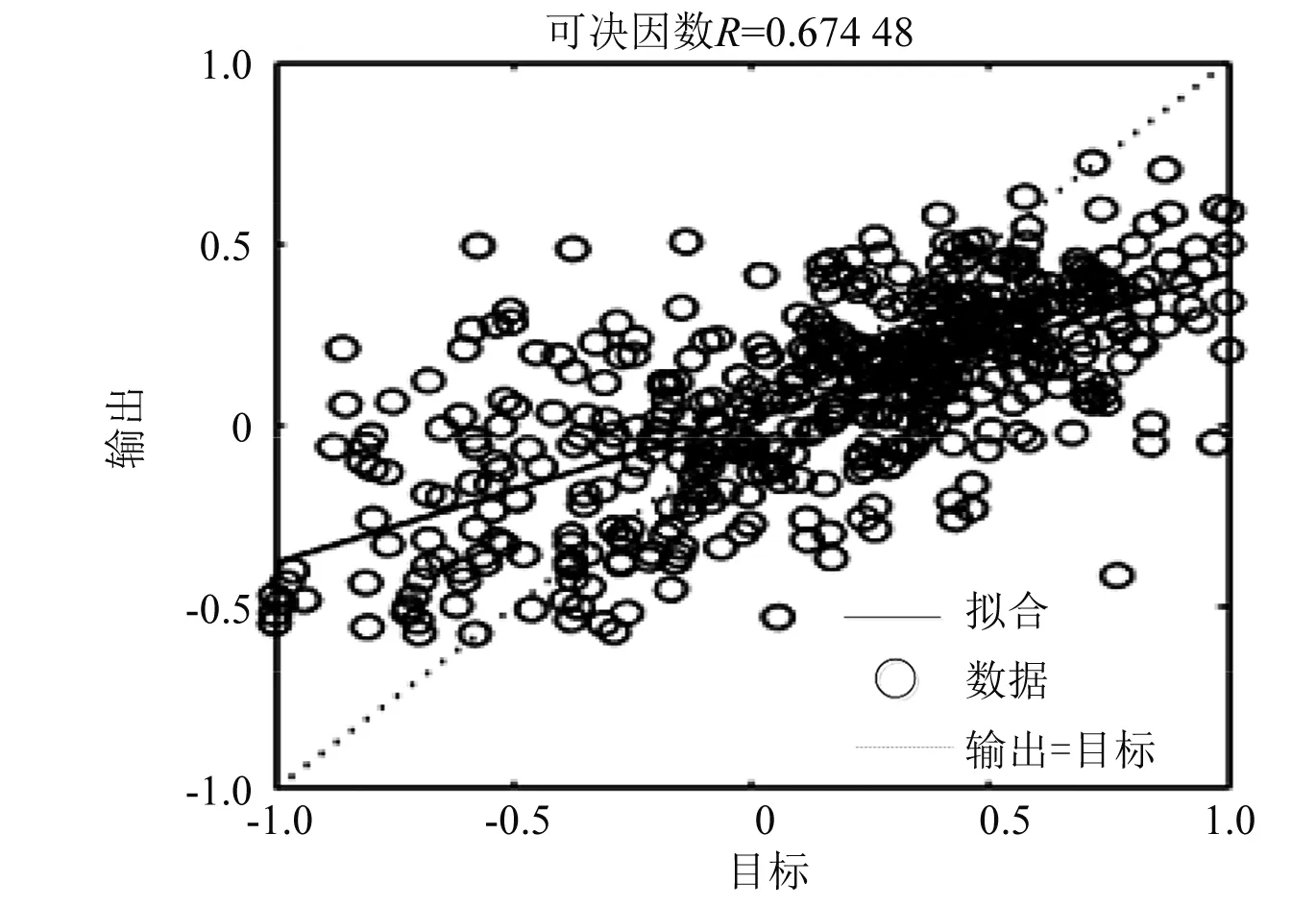
图10 粒子群优化初始权值与阈值网络训练拟合结果

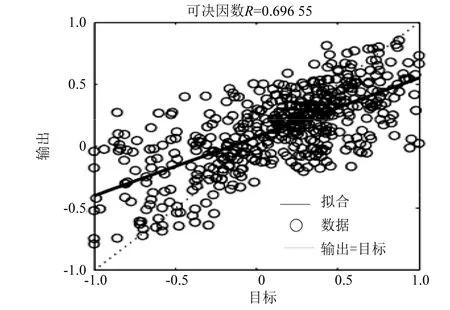
图11 差分进化优化初始网络训练拟合结果

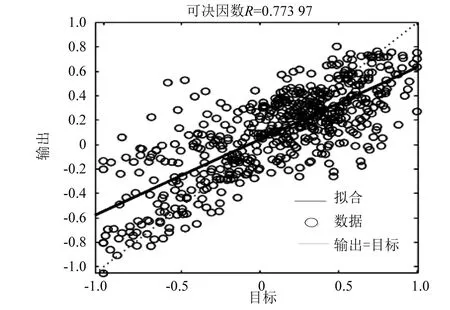
图12 差分-粒子群优化初始权值与阈值网络训练拟合结果

表1为网络训练结果。结果表明，差分-粒子群优化算法于其他三种算法中耗时最短，误差最小，网络性能表现最佳，证明了差分粒子混合优化算法用于改进BP神经网络，网络性能获得较大改善。

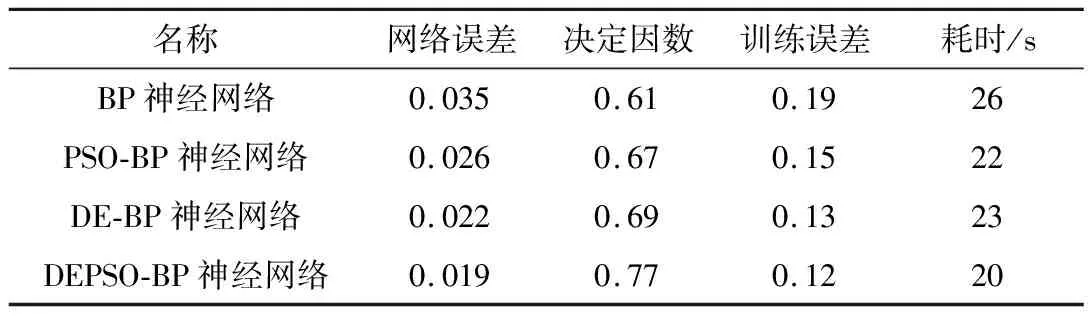
表1 网络训练结果

基于差分-粒子群容量优化算法配置储能规模为4 MW/6 MWh，采用三充三放的运行策略，储能通过峰谷价差套利年节省电费约为223万元，不计储能损耗及税收储能回收期约为7年。

4 结束语

本文在已有研究的基础上，提出了一种基于差分进化和粒子群混合优化算法的用户侧储能容量优化方法。在传统的粒子群优化算法中加入差分进化算法作为辅助变异算子，改变粒子群优化算法的速度更新公式，提高了计算效率以及全局搜索能力。仿真结果表明，采用差分进化粒子群算法时，收敛速度较差分进化法和粒子群算法有明显的提高，从而具有更强的寻优能力，成功地解决了用户侧储能系统的容量优化问题，提高了用户侧储能的经济性。