基于k-means聚类方法的曲线按比伸缩置换缺失数据补全法

杨亚洲，钱秋明，梁鸭红

(云南电网有限责任公司普洱供电局，云南 普洱 665000)

0 引 言

对于电力负荷的预测，很大程度上依靠对大量历史用电负荷的历史数据进行分析处理。因此，电力负荷预测结果的准确性，往往跟所提供的以往用电负荷历史数据的可靠性以及有相关因素的资料的准确性等因素紧密相关。目前，我国各级电力调度中心对历史数据进行采集的系统多为SCADA(数据采集与监控)系统[1]。由于采集设备故障、通信网络故障和程序错误等原因，在数据库存储的电力负荷历史数据会出现空值，即发生数据缺失现象。数据缺失现象会对负荷预测的准确性产生不良影响。研究缺失数据的补全方法具有重要的意义。

用于补全数据的方法主要分为统计法和分类法两种。统计法包括传统的数学方法和新兴的机器学习算法。传统的数学方法包括线性插值法补全法[2]和样条插值拟合补全法等。王雁平直接将负荷按照前N天的平均负荷曲线对缺失数据进行补全，该方法没有充分考虑负荷变化规律[3]。传统的统计算法补全数据计算量小，易于实现，但是补全的准确度低。机器学习算法通过复杂的数据挖掘处理，能够大幅提高数据补全的准确度如神经网络[4]、贝叶斯神经网络[5]、k-邻近算法[6]，但是这些算法计算成本高，实际应用困难。已有研究表明，分类法相比于统计法在缺失数据补全上具有明显优势。李晓飞提出了基于k-means算法的缺失数据填充方法，通过将数据聚类寻找特征数据，选择出现最多的离散性数据进行填补[7]。赵天辉基于统计模糊矩阵分析用电模式找到符合水平相似日，根据相似程度选择权重，对异常数据利用加权平均值进行修复[8]。林顺富通过灰色关联分析和模糊聚类找出与带补全日负荷向量隶属值最大的两条特征负荷曲线，以隶属度为权重进行加权平均修复[9]。

针对现有数据补全法的不足，本文提出了一种基于k-means聚类方法的曲线按比伸缩置换法，通过把其日负荷向量所属类的质心向量的相应数据按照一定的比例伸缩变换，替换到空缺数据部分，完成数据补全。该方法补全精度较高，受缺失数据量、缺失数据位置的影响小，而且计算成本相对较低。

1 基于k-means 聚类方法的曲线按比伸缩置换法数据补全原理

1.1 数据补全的目的与应用

数据补全，即探寻数据内部的规律，补全数据中缺失的数据。在电力系统中，数据补全是负荷预测中不可缺少的一步。目前，我国各级电力调度中心对历史数据进行采集的系统多为SCADA(数据采集与监控)系统。由于采集设备故障、通信网络故障和程序错误等原因，在数据库存储的电力负荷历史数据会出现数据缺失现象。一方面，负荷预测的准确度很大程度依赖于历史数据的准确度，缺失数据明显会降低历史数据的准确度；另一方面，空置(不正常零值)比有误差的历史数据对预测算法准确度的影响更大。因此，研究数据补全方法具有重要意义。

1.2 曲线按比伸缩置换原理

曲线按比伸缩置换的原理是：用和含有缺失数据曲线趋势相似的曲线的相应部分，根据其与原缺失数据的首尾差值按比例伸缩，置换原曲线的缺失部分，从而达到补全效果。

图1(a)为待补全的数据向量，其中点a到点b的数据为缺失数据。图1(b)为与图1(a)趋势相似的曲线，图中c、d分别与a、b相对应。补全数据的方法为将图1(b)cd段曲线经过伸缩变换，连接到ab段曲线补全数据。

假设待补全数据的个数为n，即ab之间有n个采样点发生数据缺失，为填补待填补数据两段的差值，cd曲线中的每一个点都要按比例伸缩一定步长，如式(1)所示：

(1)

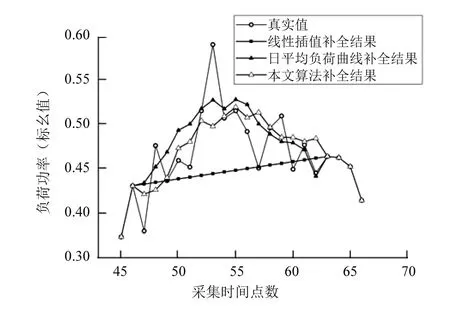
那么，第i(i

y(i)=yb+(ya-yc)-step×i

(2)

填补结果如图1(a)中虚线所示。

图1 数据补全算法示意图

1.3 基于k-means聚类方法的曲线按比伸缩置换法补全数据具体实施步骤

由于考虑到同一负荷在时间上具有一定的规律特性，即负荷在客观条件如温度和节假日属性等相似的日期具有相似的负荷曲线，采用基于k-means聚类方法的曲线按比伸缩置换法，达到提高数据补全精度，减小数据补全精度受缺失数据位置、缺失数据数量影响的目的。

本文提出的基于k-means聚类方法的曲线按比伸缩置换法的具体步骤如下：

步骤一：以日负荷向量的形式输入负荷数据。

步骤二：把日负荷向量分为完整向量和含有缺失数据的向量。含有缺失数据的向量为待补全向量。

步骤三：把完整的日负荷向量进行聚类，并求出每一类的质心向量。

步骤四：将待补全向量根据与各类质心向量欧式距离最小进行分类。

步骤五：将待补全向量所属类的质心向量作为与待补全向量具有相似负荷曲线的向量，根据本文2.2小节中给出的数据补全方法，将缺失数据补全。

2 算例分析

本文算例中电力负荷历史数据采用某省某地产发展公司的用电功率数据。该数据共225天，每天采集96次，每隔15 min进行一次采集。

同时，本文还收集了与电力负荷数据匹配的天气数据——日平均气温和对应日期的节假日属性。

为了测试本文提出的数据补全方法的效果，本文构造了20段缺失数据。具体做法如下：在已有数据中随机选择20天数据作为含有缺失数据的日负荷向量，缺失数据起始位置随机，长度随机1到30不等。

2.1 缺失数据补全

本文中每天96点数据构成一个向量，共225个向量，其中完整的向量为205个。将这205个向量以不同分类类数到进行试验，聚类结果如图2所示。

图2 k不同取值的聚类误差和

图2中：横坐标为类数k的取值，范围为1到25；纵坐标为依据该k值进行分类，所有向量到其相应分类的质心向量的欧式距离之和。当k从1增加到5，聚类效果明显提升；当k≥6，聚类效果提升效果趋于平缓。因此针对本文所使用的数据集，选择k= 6。根据式(1)～式(4)分别对缺失数据进行补全，补全误差如表1所示。

表1 缺失数据补全误差

图3为某日数据补全结果，该日从第47个采集点到第62个采集点，共模拟丢失16个采集点的数据。可见，基于k-means聚类的曲线按比伸缩置换补全法补全的数据值更接近数据的实测值，比线性插值补全数据和日平均负荷曲线补全数据的效果好。

图3 某日缺失数据补全结果

2.2 数据补全精度对基于支持向量机回归算法的负荷预测的影响

利用网格寻优算法对误差惩罚系数C和核函数参数g进行优化，结果为C=10.2，ε=0.01，g=2.7。

分别利用线性插值法和基于k-means聚类置换法补全的数据进行支持向量机负荷预测，计算预测误差，结果如表2所示。

表2 支持向量机预测结果对比

从表2结果可以看出，数据补全的准确度对支持向量机预测结果有一定的影响。由于基于k-means聚类置换法补全的数据要比线性插值法补全准确度高，因此应用其数据的预测准确都会提升。

3 结束语

本文提出的基于k-means聚类的曲线按比伸缩置换法，由于其应用了电力系统辐射数据具有时间周期相似性的特点，明显地提高了数据补全的准确度。并且，该种方法具有受缺失数据长度、缺失数据位置影响较小的优点。在一定程度上，提高数据补全准确度可以提高预测的准确度。数据补全对于负荷预测，乃至光伏发电和风力发电等发电功率预测都起到至关重要的作用。

本文进一步研究方向：一方面要优化数据采集存储系统，减少数据的丢失；另一方面，需进一步研究电力负荷曲线的特征提取与利用，更好地完成缺失数据补全的任务。