Reissner-Nordström时空下试验粒子的进动研究

李松远,林文斌

(南华大学 数理学院,湖南 衡阳 421001)

0 引 言

广义相对论解释了水星的近日点进动问题，这也是检验广义相对论正确性的三个著名现象[1-4]之一。广义相对论的创立不仅可以对引力的理解提供新的见解，也是现代宇宙学[1]的基础理论。通过计算太阳系其他行星对水星的扰动影响，牛顿力学计算出每百年531角秒的岁差，而观测得出的岁差预测值是每百年574角秒。这个差是由Urbain Le Verrier在1859年的观察所得。他猜想可能是位于水星以内的一颗小行星对水星的引力导致这个差距，但是这个行星一直没有找到。有科学家提出，可能是因为水星发出黄道光的物质对水星产生影响[5]，但这并不能解释其它行星类似的进动差。爱因斯坦第一次对试验粒子在Schwarzschild时空下的运动研究，通过对小参数r的幂展开被积函数，并在展开式中只保留线性项，得到了水星进动的公式[5]。研究行星进动时，人们的关注点在于运动的频率而非轨道细节，处理这样的问题时，作用角变量将会是很有效的工具[6]。作用角变量是一组正则坐标，应用作用角变量，可以先不求解运动方程，就能得到振动或旋转的频率。在哈密顿力学中，作用角变量法也可应用于摄动理论，特别是用于决定缓渐不变量。应用作用角变量法可以得到试验粒子在Schwarzschild时空下近圆轨道和椭圆轨道的进动[7]。本文利用作用角变量法给出了试验粒子在带电荷的黑洞[8]附近即Reissner-Nordström(R-N)时空下近圆轨道进动的表达式。

1 时空背景和运动方程

R-N度规[9]为：

dτ2=f(r)dt2-f(r)-1dr2-r2dθ2-r2sin2θdφ2

(1)

其中

(2)

因该时空为球对称，考虑无自旋试验粒子处于该时空下动力学完备微分方程组[5]为：

(3)

(4)

(5)

其中h和E为常数。

2 R-N时空中粒子的运动方程

由式(5)可得：

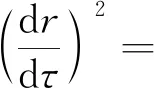
(6)

令

(7)

其中E1为粒子能量，于是可将式(6)写为：

(8)

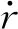
由式(8)可以选择拉格朗日量为：

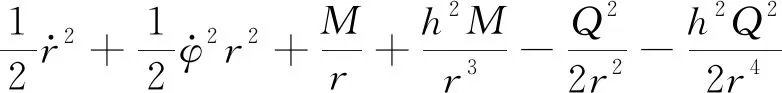
(9)

(10)

其中ψ为广义坐标r和φ，可以得出：

(11)

将式(9)带入式(11)中可得到：

(12)

(13)

由式(3)知，可取C=h，则上述两方程为：

(14)

(15)

式(15)与式(5)两边对τ求导得到的结论一致，且式(14)与式(3)等价，因此，当式(12)中积分常数取为h时，所选的拉格朗日量是合理的。

3 哈密顿-雅可比方程和粒子的作用角变量

通过式(9)，可将广义动量[6]表示为：

(16)

哈密顿量可表示为：

(17)

因哈密顿量H不显含τ，于是应用哈密顿-雅可比方法可将哈密顿量的主函数写为：S=-E1τ+W(r，φ)，W(r，φ)为特征函数，哈密顿-雅可比方程为：

(18)

对W进行变量分离，即

W=W1(r)+W2(φ)

(19)

于是

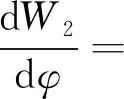
(20)

因为φ为哈密顿函数中的循环坐标，所以

(21)

其中α为一常数，所以式(20)可以写成：

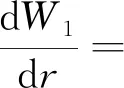
(22)

于是作用变量可以写成：

Jφ=∮Pφdφ=∮αdφ=2πα

(23)

(24)

可将式(24)写成

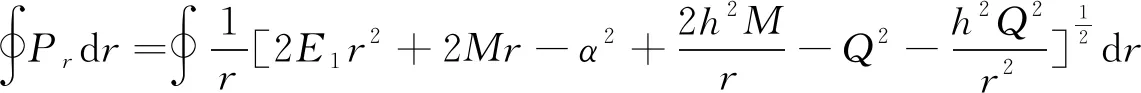
(25)

4 近圆轨道下的进动

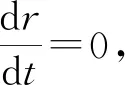
(26)

当粒子在半径为R的圆轨道上时，上式左边对R的导数也必须为零，所以

(27)

解得

(28)

(29)

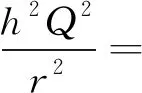
(30)

将上述两式代入式(25)得

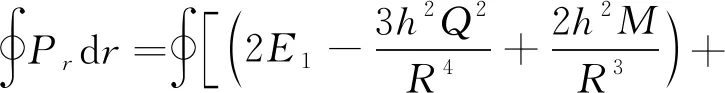
(31)

积分上、下限分别为R-δ和R+δ。令

(32)

于是式(31)可写成

(33)

其积分结果为[6]：

(34)

即

(35)

利用式(35)解出E1为

(36)

代入式(23)可得

(37)

解得运动的两个频率分别为：

由式(14)可知2πh=Jφ，于是

(40)

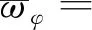
(41)

(42)

代入式(28)后泰勒展开为：

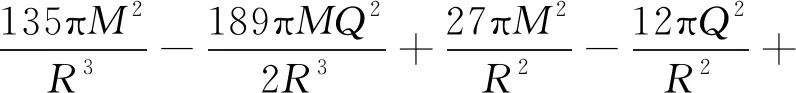
(43)

式(43)与M.Heydari-Fard等人[10]的研究在考虑黑洞自旋为0时的结论一致。

5 结 论

本文根据R-N度规和该时空下无自旋试验粒子的完备运动微分方程组给出了试验粒子的运动方程，推导出了该粒子的哈密顿-雅可比方程。利用试验粒子的哈密顿-雅可比方程得出了处于近圆轨道下试验粒子的作用角变量，根据试验粒子的作用角变量得出了经过一个周期后的进动表达式，并与相关近似解做了比较。