炮射高速运动目标图像预处理方法研究

曹志元，马春茂，钞红晓

(西北机电工程研究所，陕西 咸阳 712099)

在研制过程中，炮射武器装备需要通过多种测试手段去获取其运动位移、速度、加速度、姿态等高动态运动参数作为武器状态、性能的验证与评估依据[1]。基于高速摄像的动态运动参数获取技术因其测量精度高、响应快、拍摄信息量大等突出优点，能够直接测量并获得大量准确的时空信息，使其成为炮射武器研究领域广泛使用的测量技术[2]。但由于炮射武器的自身特性和外场试验环境的复杂性，常导致该技术获得的高速连续帧图像不够清晰，无法进行有效的参数获取。所以通过对高速摄像采集到的连续帧图像进行预处理来提高图像的辨析度，对解决连续帧图像中常因烟尘虚化、运动模糊、亮度过低等引起的高动态运动参数处理问题有十分重要的意义。

炮射武器在发射时，产生的烟尘、火光等导致画面中的被摄目标被虚化；弹丸等高速目标的飞行速度最高可达2 500 m/s，一般为获得足够清晰明亮的图像需要将曝光时间调到最大，但这会导致被摄高速目标出现拖影等运动模糊情况，若降低曝光时间，又会导致整个图像过暗而不清晰，无法选择合适的曝光时间；同时供弹、传动结构等被摄目标经常会被其他结构遮挡，导致目标过暗，使被摄目标的具体细节无法观测。

笔者主要针对炮射武器试验过程中，通过图像处理技术来解决上述基于高速摄像和图像处理的动态运动参数获取时所存在的3种典型问题，使得能从连续帧图像中获得更多、更精确的所需信息。

1 图像预处理技术

图像处理技术主要目的是改善图像质量，通过图像增强和复原处理退化图像，实现去除噪声和提高图像的像素分辨度等[3]。针对试验过程中存在的烟尘导致被摄目标被虚化、高速目标运动模糊和被摄目标过暗使细节无法观测这3种典型图像质量问题，通过使用合适的图像处理算法对退化图像进行恢复[4]。

同时使用图像质量客观评价方法，通过梯度函数、拉普拉斯算子、Vollaths函数和信息熵对处理前后的图像进行定量分析[5]。Tenengrad梯度函数是一种基于梯度的函数，提取水平和垂直方向的梯度值并经过Sobel算子处理，值越大，代表图像边界越清晰；拉普拉斯函数对被评价图像中的像素在其3×3领域内使用拉普拉斯算子进行计算，然后将计算出的值求和再取平均，值越大则被评价图像越清晰，质量越好；Vollaths函数又称自相关函数，反映空间两点的相似性，正焦图像边缘清晰锐利，像素点之间相关程度低，离焦图像像素点相关程度高；信息熵函数用来描述信息的丰富程度，获得图像中每个灰度在整幅图像中出现的概率，最终获得灰度值的总期望，熵值大，说明图像色彩艳丽、图像轮廓清晰。

1.1 暗通道去雾算法

炮射武器在发射过程中常伴有大量的烟尘和火光，烟尘经常会遮挡一些观测目标，增加试验数据获取难度。某型空气炮试验过程中产生的灰尘遮挡弹丸上的标记等目标，导致图像质量降低，影响从图像中获取精确的试验数据。通过对图像退化原因分析，发现空气炮发射过程中所产生的灰尘遮挡图像，其暗通道与有雾图像的暗通道相同，如图1所示。

因此采用暗通道图像去雾算法去除空气炮灰尘遮挡来提高图像质量[6]，并获得了较好的效果。雾图形成模型为

I(x)=J(x)*t(x)+A(1-t(x))，

(1)

式中：I为相机拍摄到的图像；J为无雾图像；t为大气透射率；A为全球大气光成分，全球大气光A通过求取有雾图像的暗通道Jdark(暗原色先验原理)[7]，选取其中亮度最大的像素中前0.1%的像素，然后再输入图像中与以上这些像素对应的像素中取亮度最大的像素作为大气光A.

在A作为已知条件下，对式(1)两边在(x,y)领域范围内取最小值，且在(x,y)领域范围内大气光透射率均为t(x,y)，将已知的有雾图像I、大气光成分A和透射率t带入式(1),可得到无雾图像J：

(2)

基于上述暗通道图像去雾算法来对图像进行去烟尘操作，可得如图2所示的处理结果。

将图2中所关心的区域提取出来进行分析，如图3所示。

通过前文提到的4种图像质量客观评价方法，得到对图3标记位置处理前后的评价，如表1所示。

表1 基于暗通道去雾算法处理的图像质量评价

通过分析处理前后图像及表1数据可以发现，处理后的图像在烟雾遮挡部分图像增强明显，去除了由烟雾干扰导致的目标标记雾化模糊;图像质量客观评价方法中,处理后的图像的梯度函数和拉普拉斯算子的值相差较大，证明处理后的图像在边界划分上更加明显，减少了图像因灰尘导致的雾化模糊。

1.2 基于盲反卷积的L-R算法

炮射武器试验中由于曝光时间过长时，可导致弹丸等高速运动目标出现拖影、弹丸目标不清晰，以及无法观测弹丸飞行过程中的具体细节等情况。弹丸在曝光时间内的运动造成弹丸目标模糊，整个过程一般被看做清晰图像卷积模糊核得到模糊图像的过程，其图像退化模型如图4所示。

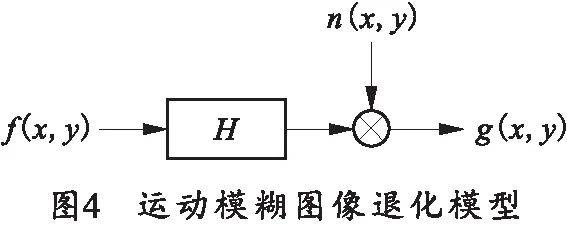
在使用L-R算法迭代去模糊之前，先要给出一个初始估计的PSF[8](Point Spread Function，PSF)，初始的PSF对后续图像的迭代去模糊非常重要，一般都是以一个全一数组作为估计的初始PSF，通过对多个估计的初始PSF进行对比，确定出一个最优的初始PSF作为L-R算法开始的PSF[9]。整个运动模糊图像恢复过程如图5所示。

L-R算法是一种非线性迭代图像恢复方法，该算法采用贝叶斯条件概率模型，假设图像中的像素值满足泊松分布，进而构造极大似然函数，并对其进行迭代求解，从而实现对退化图像的复原[10]。L-R算法为

fk+1(x,y)=

(3)

式中：fk就是第k轮迭代复原图像；g是已知退化图像；h为退化系统的PSF.

即在第k轮迭代，假设原始图像已知，即k-1轮得到的fk-1再通过L-R公式求解hk，再用hk求解fk，反复迭代，最后求得最终的f和h，因此，需要同时假设一个复原图像f0和一个退化函数h0，fi为第i次反复迭代，L-R算法迭代公式如下：

(4)

(5)

通过对图像进行盲反卷积，之后通过L-R算法迭代处理退化图像得到处理结果，如图6所示。通过4种图像质量客观评价方法对图6处理前后进行评价，如表2所示。

表2 盲反卷积的L-R算法处理的图像质量评价

通过对图6的处理结果及表2数据可以看出，处理后的图像相比于处理前的图像有明显的改良，初始估计的PSF对图像的恢复至关重要，同时L-R算法迭代的次数对画面质量也有很大影响，当迭代次数过多时，图像会出现明暗相间的条纹，即振铃效应，通常抑制振铃效应的方法有最优窗口法和循环边界法;图像客观评价方法中各个评价函数的值都比处理前提高了，证明将运动模糊图像去模糊处理对图像质量有明显的提升。

1.3 变换函数算法

在炮射武器试验测试时，有时需同时拍摄多个目标，部分目标亮度较高，部分目标亮度较低，使拍摄到的图像存在较强的明暗差异；或有时因天气原因，导致整幅图像亮度较低。这些情况都会导致暗区域的目标无法精确观测。图7(a)为某型火炮供弹结构图，由于其处于炮体下部，光线被遮挡，导致目标亮度较低。通过变换函数对较暗区域进行图像增强来提高图像质量[11]。变换函数通过对不同灰度值的点进行划区域控制，较暗区域可通过函数进行增强处理，较亮区域可进行弱化处理，通过不同的函数处理指定区域，操作灵活，能根据实际情况进行调整[12]。

分段线性变换逻辑公式：

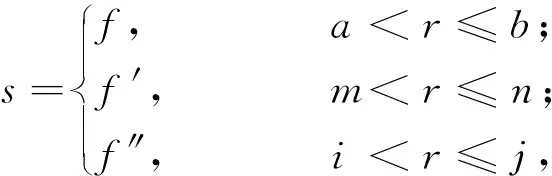
(6)

式中：s为通过函数变换得到的值；f、f′、f″均是关于的r函数，其可以根据具体的需要进行调整；在a、b、m、n、i、j∈图像灰度范围内，r为图像某像素点的R、G、B通道的灰度值。

通过变换函数对图像中较暗区域进行增强处理，如图7(b)所示。相比于原始图像，经过变换函数处理过后的图像在暗区域的内容更易被辨识或识别。通过4种图像质量客观评价方法对图7处理前后进行评价，如表3所示。

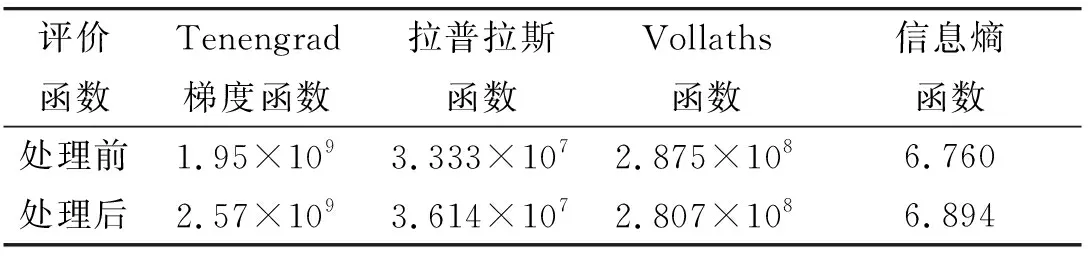
表3 基于变换函数算法处理的图像质量评价

通过分析处理前后图像及表3数据可以发现，在暗区域的目标通过变换函数处理后可以明显分辨细节和轮廓，证明该方法对暗区域图像的细节有明显增强的作用;图像客观评价方法中处理后的图像各个评价函数相比于处理前均有所提升。

2 实验室试验验证

笔者所使用的4种图像质量客观评价方法在一定程度上能反映图像的质量情况，但是不能准确衡量处理后的图像所含有用信息确实有所提升。所以通过实验来进一步验证图像处理对实际高速连续帧图像数据准确度的影响。实验原理图如图8所示。

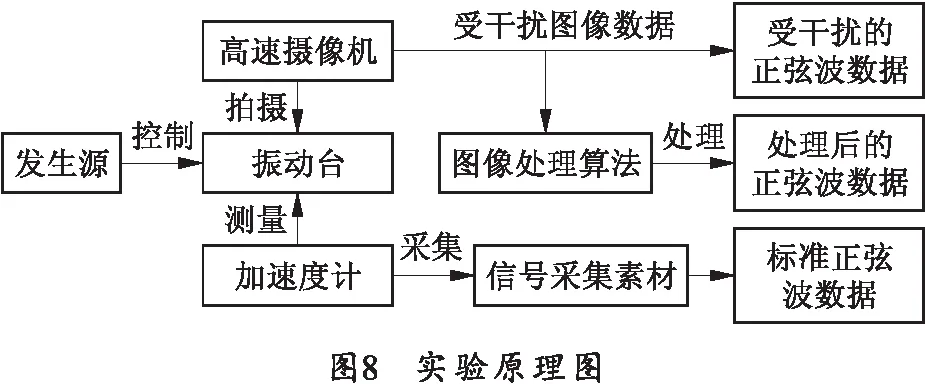
通过信号源控制振动台产生一个稳定的正弦波形；将一个标准加速度计粘贴在振动台上部，用以采集振动台产生的实际的正弦波形作为标准正弦波；在有干扰的情况下(加雾、增大曝光时间、低亮度环境)，使用高速摄像机获取振动台振动过程中的高速连续帧图像数据，之后通过上文所提及的图像处理算法来处理图像，如图9～11所示。进而通过标记跟踪得到处理前后图像的正弦波数据与标准正弦波数据和其相对误差，如表4所示。

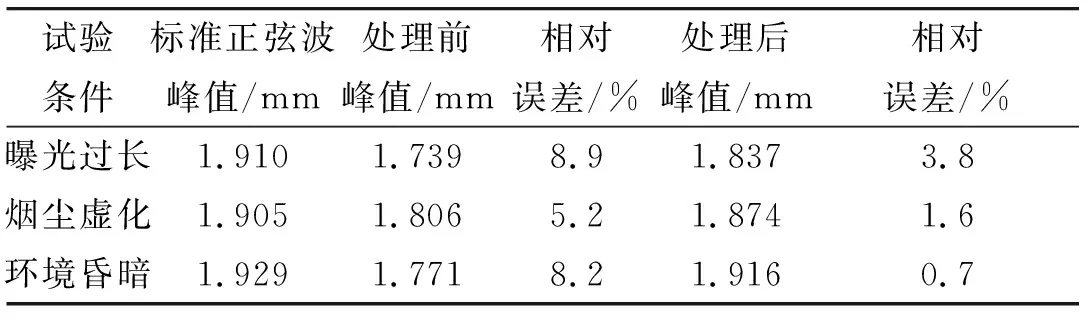
表4 试验对比结果

根据最终处理得到的数据可以看出，处理后的连续帧图像得到的正弦波峰值比有干扰的未处理图像的正弦波峰值相对于标准正弦波峰值的误差更小。同时在处理曝光时间过长的图像过程中，跟踪标记时频繁丢失目标，有时需要手动定位，而处理后的目标跟踪很稳定。也说明处理得当对退化图像有很好的修复作用，能便于更好地获取图像中所记录的数据。

3 结束语

针对基于高速摄像技术的动态运动参数测试在炮射武器试验过程中的3种典型图像质量问题，通过选择合适的图像处理算法并进行优化，解决了高速连续帧图像的图像退化所带来的目标观测困难和数据准确度的问题。笔者通过图像客观评价函数和实验验证了图像预处理的可行性，通过图像处理算法处理高速连续帧图像的辨析度，提高了从图像中获取动态参数数据的准确度，保证了基于高速摄像技术的动态运动参数测试技术在复杂测试环境和多种干扰因素下的适应性。