基于组合模型预测火炮初速的研究与应用

田珂，陈铎

(中国人民解放军63850部队，吉林 白城 137001)

现代战场环境中，能够精确打击敌人成为火炮射击的重要目标，而这决定于火炮射击精度是否准确。影响火炮射击精度的因素有很多，火炮初速是火控系统解算或射表计算的重要参数之一，直接影响火炮系统的命中精度[1]。如何在不经试射的条件下把握短暂的战机准确打击目标，对火炮初速预测就成为了重要的研究目标。目前预测火炮初速的方法有很多[2-4]，这些单一模型的优点是建模简单，缺点是只能预测出火炮初速中的某一特征，预测的精度有限。火炮初速可以看做以弹序为参数的时间序列，单一模型无法同时提取出火炮初速中的线性成分和非线性成分，导致预测精度不理想。根据Bates和Granger对组合预测模型的研究，可以把多种预测方法所得到的预测结果进行综合考量，这样能较大限度地利用多种预测方法的样本信息，考虑问题更全面，减少单个预测模型受各种随机因素的影响，进而提高模型预测的精度[5]，因此选择利用ARIMA模型、GM(1,1)灰色模型与BP神经网络模型构建组合模型提高预测火炮初速的精度。

1 ARIMA模型建模

1.1 平稳性检验

检验时间序列的平稳性，通常有时序图检验和单位根检验。由于时序图检验平稳性的方法带有一定的主观性，精度不高，所以需要利用ADF单位根检验法准确检验平稳性[6]。ADF单位根检验法就是对时间序列构造检验统计量t，根据t对应的概率p的值与临界统计值进行比较来检验时间序列是否有单位根。临界统计值通常设为0.05，如果p<0.05，说明原始序列不存在单位根是平稳的；如果p≥0.05，说明原始序列存在单位根是非平稳的。

1.2 白噪声检验

通常用LB统计量检验法检验时间序列是否为白噪声序列。给定临界统计值α=0.05，如果检验统计量t对应的概率p≥0.05，说明原始序列为白噪声序列；如果检验统计量t对应的概率p<0.05，说明原始序列存在相关性为非白噪声序列。

1.3 模型识别

根据平稳非白噪声序列的自相关图(ACF)和偏自相关图(PACF)的特征就可以确定模型类别，各个模型相关图的特点如表1所示。ARMA称为自回归移动平均模型，AR(m)是自回归过程，m是自回归过程的系数，MA (n)是移动平均过程，n是移动平均过程的系数，但大多数时间序列都是非平稳的，这时就需要进行差分处理把原始非平稳时间序列转换为平稳时间序列，需要进行差分处理的时间序列模型为ARIMA(m,d,n)，称为差分自回归移动平均模型，等于是在ARMA模型的基础上进行差分处理，d是差分次数。

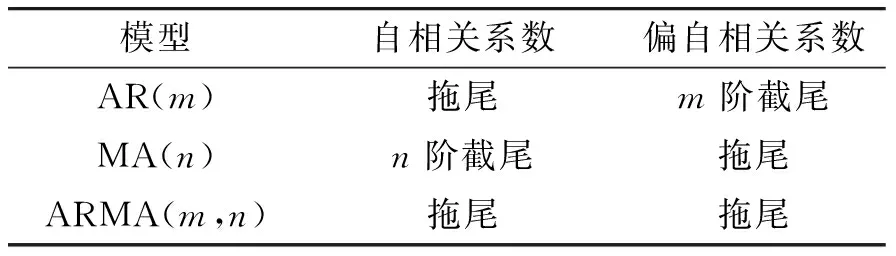
表1 ARMA模型识别原则

1.4 模型定阶及模型评价

通常采用AIC准则(最小信息准则)和BIC准则(舒瓦特信息准则)确定模型阶数，与自相关图和偏自相关图相比，这两种准则能更准确地确定模型阶数，原则上使得AIC和BIC值最小的模型就是最佳模型。通常采用极大似然估计法来估计时间序列模型的相关参数。要检验所建立的模型是否合理,通常用两个指标进行评价：

1)判断模型残差是否是平均值为0且方差为常数的正态分布;

2)模型的残差是否满足独立性要求，即模型残差是否是白噪声。

2 GM(1,1)灰色模型建模步骤

GM(1,1)模型是应用最为普遍的一种灰色动态预测模型，设有原始序列如下所示：

y(0)=(y(0)(1),y(0)(2),…,y(0)(n)).

(1)

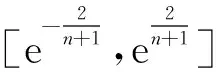
(2)

对y(0)序列作一次累加得到：

y(1)=(y(1)(1),y(1)(2),…,y(1)(n)).

(3)

对y(1)可建立一阶线性微分方程：

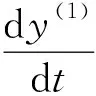
(4)

求解微分方程，得到y(1)预测模型：

k=1,2,…,n,

(5)

式(5)是由y(0)累加得来的，对其进行累减得到y(0)的预测模型：

k=1,2,…,n.

(6)

通常用后验差检验方法评价GM(1,1)模型预测结果的好坏，主要根据检验结果中的后验差比值C和小误差概率P这两个数值来检验。具体检验标准如表2所示。

表2 GM(1,1)预测结果评价表

3 BP神经网络模型建模

BP神经网络是最常用的人工神经网络，是一种按误差逆传播算法训练的多层前馈网络，由输入层、隐含层、输出层构成，每层由若干个节点组成，每一个节点代表一个神经元，上一层与下一层通过权值链接，典型的BP神经网络通常为含有1个隐含层的3层网络结构。BP神经网络算法的学习过程分为信号的正向传播与误差的逆向传播:

1)正向传播是指输入信号从输入层进入网络经过隐含层的处理后传向输出层。

2)如果输出层的实际值与期望值不相符或者误差太大，则进入误差的逆向传播过程，将输出误差经隐含层传播到输入层并修改权值与阈值。

3)信号的正向传播与误差的逆向传播导致权值和阈值的修改过程是循环往复进行的，这个过程一直持续到输出的误差逐渐减少到可接受的程度或达到设定的学习次数为止。

BP神经网络具有非常强的自适应和推广概括能力，特别适用于求解内部机制复杂的问题，适合用于火炮初速预测，一个3层BP神经网络模型可以实现从输入到输出的任意非线性映射[8]。

4 组合模型建模及模型评价

由于火炮初速是一种特殊的时间序列，既含有稳定的不变规律又具有一定的随机性，即同时包含线性特征和非线性特征，而ARIMA模型和GM(1,1)模型都属于线性预测，能够提取出火炮初速中的线性特征，BP神经网络模型属于非线性映射模型，能够提取出火炮初速中的非线性特征，所以为了充分发挥各个模型的优势，最大限度提升预测精度，利用ARIMA模型、GM(1,1)模型与BP神经网络模型建立组合模型，既具有线性预测能力又具有非线性预测能力。组合预测模型就是先利用每个模型对时间序列进行预测，然后对单项预测结果使用适当的方式进行加权平均，最后把加权平均值作为最终预测结果的一种方法，具体原理是利用单项预测方法的误差平方和计算出权系数，再乘以单项预测值就得到组合模型预测的结果，具体数学原理如式(7)和(8)所示[5]：

(7)

(8)

选取3组不同火炮初速数据来分析验证各个模型预测火炮初速精度的高低，3组初速数据分别记为DATA1、DATA2和DATA3，DATA1和DATA3分别有29发初速数据，分别将DATA1和DATA3的第1～25发作为训练数据，第26～29发作为测试数据，每个训练数据建模预测出一发初速，再把下一发初速的真实值带入训练数据再预测下一发，最后分别得到DATA1和DATA3的第26～29发初速数据的预测值，通过与各自的第26～29发真实值进行比较，判断各个模型预测精度的高低。DATA2共有65发初速数据，把DATA2的第1～55发初速作为训练数据，第56～65发初速作为测试数据，每个训练数据建模预测出一发初速数据，再把下一发的真实值带入训练数据再预测下一发，最后得到DATA2第56～65发初速数据的预测值，与真实值进行比较，判断模型预测精度的高低，先以DATA1为例来分析各个模型建模预测的过程。

4.1 ARIMA模型实验验证

DATA1第1～29发数据的时序关系如图1所示。从图1中可知DATA1第1～25发数据并没有在某一固定常数上下浮动，而是随着时间在做随机波动，有轻微单调向上的趋势。

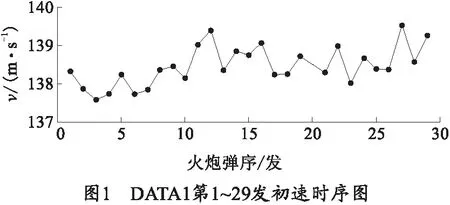
利用Rstudio软件检验DATA1第1～25发数据的单位根得到的t统计量为0.304，对应的p值为0.704 5，大于临界统计值0.05，所以DATA1第1～25发数据是非平稳的。经过检验确定DATA1第1～25发数据为一阶差分平稳非白噪声序列，满足建立时间序列模型的前提条件。检验DATA1第1～25发数据一阶差分后的自相关图和偏自相关图均呈现出拖尾的现象，所以建立的模型类别为ARIMA(m,d,n).

为了准确确定模型阶数，利用BIC信息准则确定出在m=1～5，n=1时模型最优，因此对 ARIMA(1,1,1)、ARIMA(2,1,1)、ARIMA(3,1,1)、ARIMA(4,1,1)、ARIMA(5,1,1)进行对比，使得BIC值和AIC值最小的模型就是最佳预测模型[9]，对比结果如表3所示。可以确定ARIMA(1,1,1)就是最佳预测模型。利用极大似然估计的方法估计出模型ARIMA(1,1,1)[9]的参数为(-0.163 3，-0.538 1)，分别为自回归过程的系数和移动平均过程的系数。

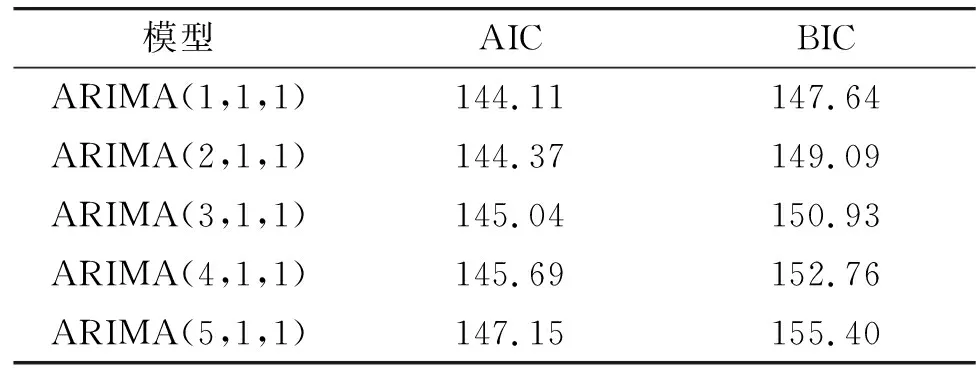
表3 模型对比

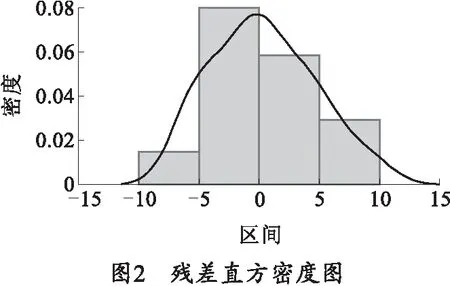
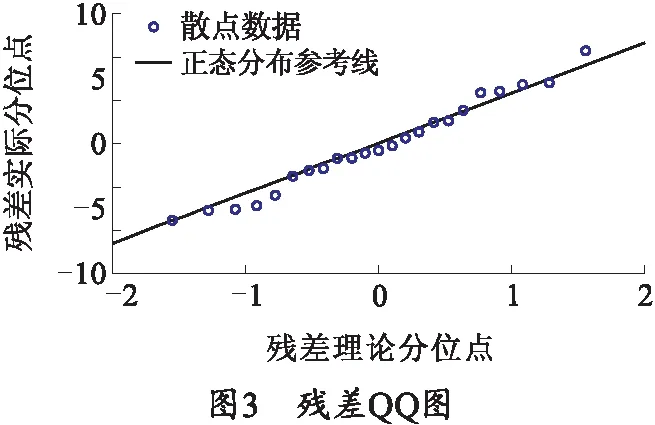
绘制ARIMA(1,1,1)模型残差的直方密度图和残差QQ图，分别如图2、3所示。残差直方密度图横坐标代表残差分布的区间大小，纵坐标代表每个区间残差分布的密度大小。从直方密度图可以看出模型残差基本上服从均值为0、方差为常数的正态分布。残差QQ图用来检验残差是否服从正态分布，纵坐标代表残差实际分位点(实际分布情况)，横坐标代表残差理论分位点(标准正态分布的分位点)，圆圈表示残差实际分位点与理论分位点配对形成的散点数据，直线是根据实际分位点与理论分位点绘制的正态分布参考线，如果残差服从正态分布，那么图中主要的散点数据应该分布在直线附近，图3显示大多数数据点分布在一条直线上，所以残差的正态性通过了检验[10]。

为了排除主观性，更准确地检验残差正态性，利用Shapiro-Wilk检验法对m1-residuals的正态性进行检验残差用统计指标residuals表示，m1代表所建立的模型，检验结果中的p值反映m1-residuals服从正态分布的概率，p值越大，说明m1-residuals服从正态分布的概率越大，p值越小，说明m1-residuals服从正态分布的概率越小，通常与临界统计值α=0.05进行比较，如果p>0.05，说明残差服从正态分布，否则不服从正态分布。利用Shapiro-Wilk检验法对m1-residuals的正态性检验结果显示t统计量的值为0.971，对应p值为0.683大于临界统计值0.05，进一步确定残差m1-residuals服从正态分布。检验m1-residuals的独立性，t统计量对应的p值为0.868 6，显著大于临界值0.05，表明残差m1-resi-duals是独立的，即m1-residuals满足白噪声的要求，所以ARIMA(1,1,1)模型通过了检验，可以用作预测模型。

利用上述建模方法，分别将DATA1第1～26发、第1～27发、第1～28发数据作为样本数据建模预测，得到DATA1第26～29发初速数据的真实值与预测值的关系如图4所示。

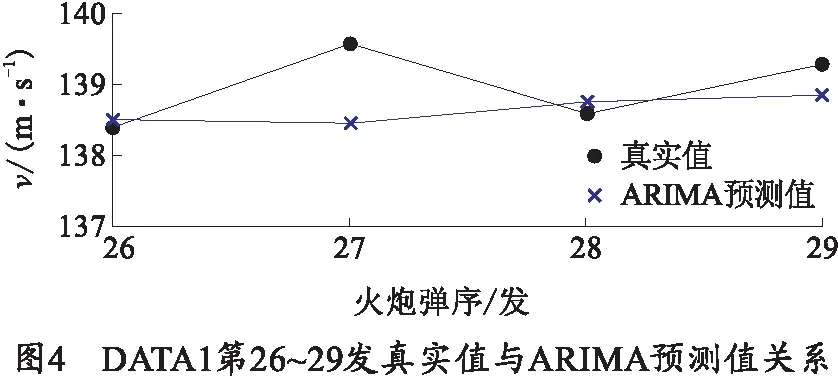
通过计算得到预测值与真实值的平均相对误差为0.320%，基本上满足火炮初速预测的精度要求[4]，所以利用ARIMA模型预测火炮初速的方法是可行的。

4.2 GM(1,1)模型实验验证

经过检验发现DATA1第1～25发初速的级比都处于区间[0.925 961 1,1.079 959 0]之中，因此DATA1第1～25发初速数据符合GM(1,1)模型的建模要求，灰色预测结果显示后验差比值C=0.503 075 3，预测精度概率P值为0.997 471 3，模型拟合精度为勉强合格[11]，可以建立GM(1,1)灰色预测模型，经过建模预测得到了DATA1第26发初速数据的预测值，利用同样的建模预测方法，分别再把DATA1第1～26发、第1～27发、第1～28发数据作为训练数据，经过建模预测最终得到DATA1第26～29发初速数据的预测值，真实值与预测值的关系如图5所示，预测值与真实值的平均相对误差为0.336%.

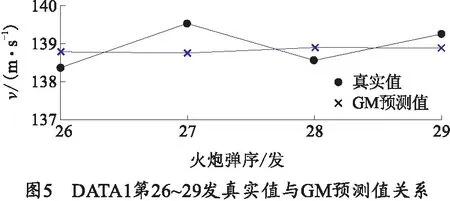
4.3 BP神经网络模型实验验证

利用3层BP神经网络建模预测，把DATA1第1～25发数据作为训练数据建立BP神经网络预测模型，把DATA1第26～29发数据作为测试数据检验所建模型预测的准确性。针对训练数据而言，按照每4发数据作为输入信号第5发数据作为输出信号构建BP神经网络模型，得到输出信号与输入信号的关系为s(v)=[s(v-4),s(v-3),s(v-2),s(v-1)]，公式左边为输出信号，右边为输入信号，这样DATA1第1～25发训练数据就构建成了行数为21、列数为5的数据集，第1～4列为输入信号，第5列为输出信号[5]。因此可以确定BP神经网络模型的输入层的节点数r=4，输出层节点数l=1，中间层的节点数u按照经验式(9)确定：

(9)

经过反复计算确定中间层的节点数u=6，误差精度设为0.001，最大训练次数设为2 000，最终经过66次训练算法完美收敛，这时把DATA1第22～25发数据作为输入信号带入到建立好的BP神经网络模型中，可以得到第26发初速数据的预测值。采用同样的方法，分别将DATA1的第1～26发、第1～27发、第1～28发数据作为训练数据建立BP神经网络模型，可以得到第27～29发初速数据的预测值，最终第26～29发真实值与预测值的关系如图6所示，预测值与真实值的平均相对误差为0.603%.

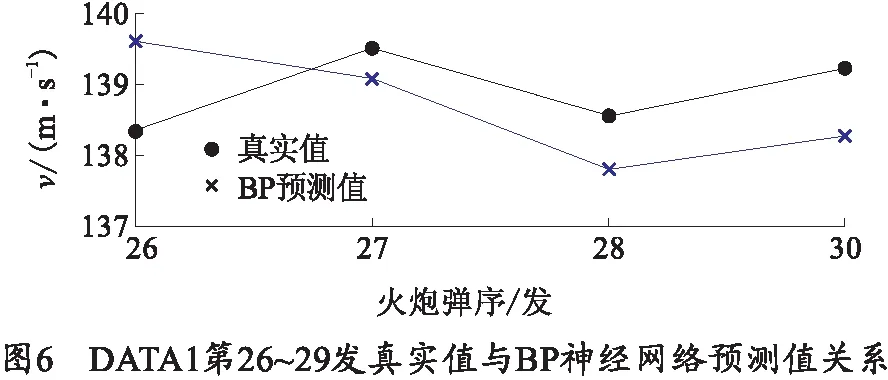
4.4 组合预测模型及实验验证

通过组合模型的建模原理可以计算出利用DATA1第1～25发数据建立组合模型时，ARIMA、GM(1,1)、BP神经网络模型的权系数分为(0.924 6，0.067 9，0.007 5)，因此分别把DATA1的第1～25发、第1～26发、第1～27 发、第1～28发作为样本数据，利用组合模型进行预测，得到DATA1第26～29发真实值与各个模型预测值的关系如图7所示，组合模型的预测值与真实值的平均相对误差为0.232%.

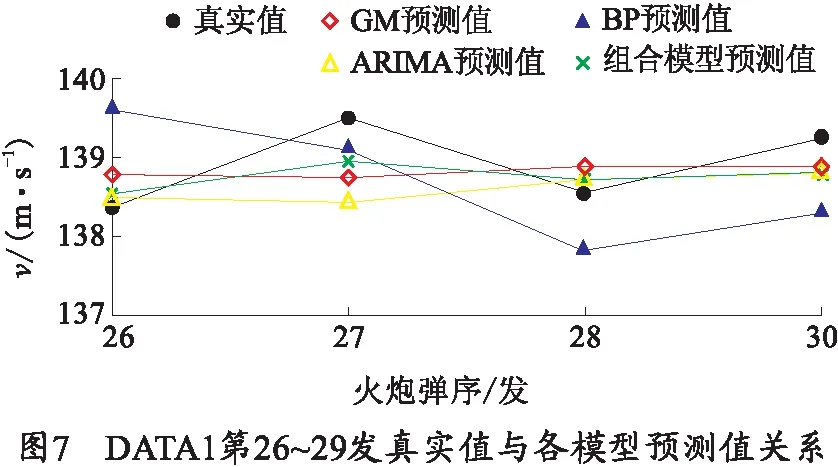
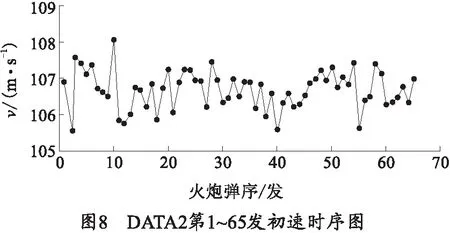
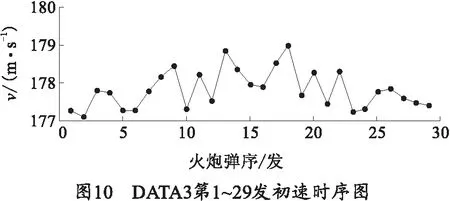
采用同样的方法对DATA2和DATA3进行建模预测。DATA2第1～65发初速的时序图如图8所示，经过建模预测得到DATA2第56～65发初速真实值与各模型预测值的关系如图9所示，其中ARIMA模型的平均相对误差为0.309%，GM模型的平均相对误差为0.312%，BP神经网络模型的平均相对误差为0.482%，组合模型的平均相对误差为0.262%.DATA3第1～29发初速的时序图如图10所示，建模预测得到DATA3第26～29发真实值与各模型预测值的关系如图11所示，其中ARIMA模型的平均相对误差为0.129%，GM模型的平均相对误差为0.221%，BP神经网络模型的平均相对误差为0.259%，组合模型的平均相对误差为0.063%.

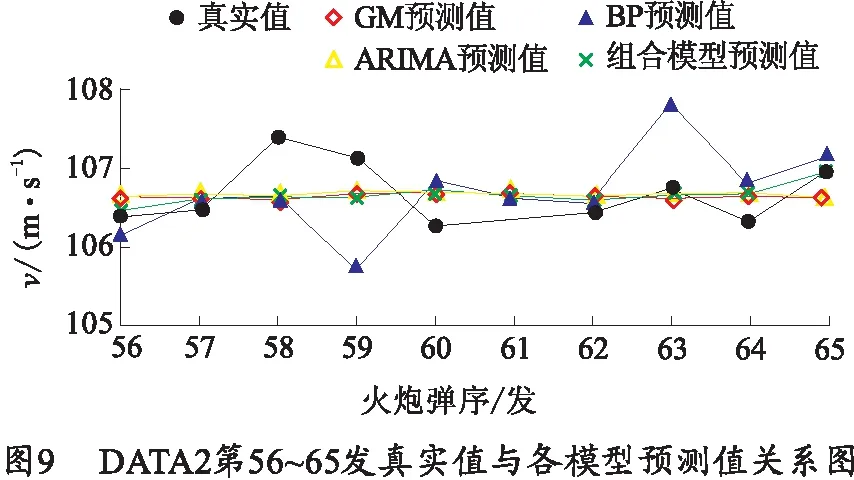
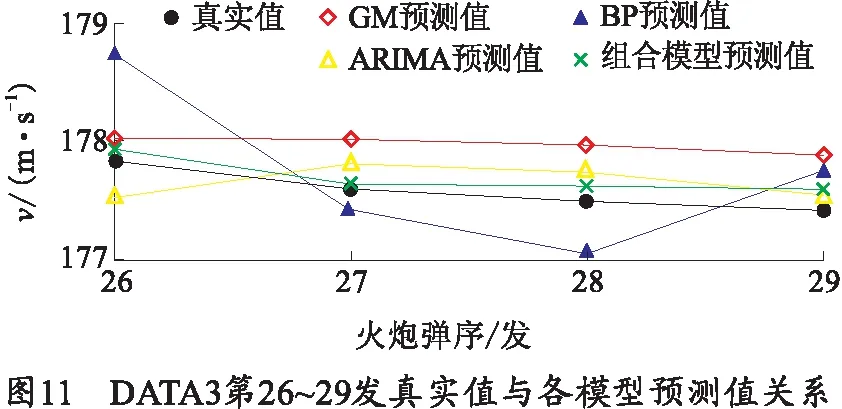
从以上预测过程及误差结果可以看出，针对3组不同的火炮初速而言，ARIMA模型、GM(1,1)灰色模型以及BP神经网络模型预测的精度高低也不一样，但是组合模型预测的初速数据的平均相对误差始终小于所有单个模型，这是因为组合模型最大限度的发挥出了3个模型的优势，预测出了火炮初速中的线性特征和非线性特征，预测的火炮初速数据精度更高，更加准确可信。

5 结束语

分别利用ARIMA模型、GM(1,1)模型及BP神经网络模型及其组合模型对3组不同的火炮初速进行预测分析，从预测结果可以看出所有模型都通过了检验，预测的数据也基本满足火炮初速的精度要求，同时对误差结果进行了对比分析，发现组合模型预测的火炮初速的平均相对误差小于所有单个模型，说明利用ARIMA模型、GM(1,1)灰色模型与BP神经网络模型建立的组合模型能有效提高预测火炮初速的精度，预测的结果也更加准确可信。